机械学习 - scikit-learn - 数据预处理 - 2
目录
- 关于 scikit-learn 实现规范化的方法详解
- 一、fit_transform 方法
- 1. 最大最小归一化手动化与自动化代码对比演示 1:
- 2. 均值归一化手动化代码演示:
- 3. 小数定标归一化手动化代码演示:
- 4. 零-均值标准化(均值移除)手动与自动化代码演示:
- fit、transform 是什么?
- 1. MinMaxScaler 归一化接口的 fit 拟合函数
- MinMaxScaler 的 fit 拟合函数代码演示:
- 2. StandardScaler 标准化接口的 fit 拟合函数
- StandardScaler 的 fit 拟合函数代码演示:
- transform 与 fit_transform 函数的理解
- 项目中使用技巧 —— fit_transform 和 transform
- 二、normalize() 方法
- 总思路参考链接:
关于 scikit-learn 实现规范化的方法详解
一、fit_transform 方法
1. 最大最小归一化手动化与自动化代码对比演示 1:
公式:
Xstd=X−X.min(axis=0)X.max(axis=0)−X.min(axis=0)X_{std}=\frac{X_{}-X_{.}min(axis=0)}{X_{.}max(axis=0)-X_{.}min(axis=0)}Xstd=X.max(axis=0)−X.min(axis=0)X−X.min(axis=0)
Xscaled=Xstd×(max−min)+minX_{scaled}=X_{std}\times(max-min)+minXscaled=Xstd×(max−min)+min ,范围 [0,1][0,1][0,1]
代码演示:
#!/usr/bin/env python
# -*-coding:utf-8-*-
from sklearn.preprocessing import MinMaxScaler
import numpy as npdata = np.array([[4,2,3],[1,5,6]])print("data格式: ",type(data))
# 手动归一化
feature_range = [0,1] # 要映射的区间
print("每一列的最小值: ",data.min(axis=0)) # axis 坐标轴 0 ,从上往下,每一列的最小值
print("每一列的最大值: ",data.max(axis=0)) # axis 坐标轴 0 ,从上往下,每一列的最大值
x_std = (data-data.min(axis=0))/(data.max(axis=0)-data.min(axis=0)) # axis 坐标轴 0 ,从上往下,列 ,标准化
x_scaled = x_std*(feature_range[1]-feature_range[0]) + feature_range[0]
print('手动归一化结果:\n{}'.format(x_scaled))# 自动归一化
scaler = MinMaxScaler()
print('自动归一化结果:\n{}'.format(scaler.fit_transform(data)))运行结果:

> 这里 [ 4 ] 算是一列,同理 [ 2 ] [ 3 ] 各自算一列
> [ 1 ] [ 5 ] [ 6 ]
在第一列中,最小的是1,第二列最小的是 2,第三列最小的是3,所以 data.min(axis) 的值便是 [1, 2, 3 ]
同理可得 data.max(axis) 的值,得出每一列的最大值 [ 4, 5, 6 ]
2. 均值归一化手动化代码演示:
公式:
Xstd=X−XmeanXmax−XminX_{std}=\frac{X-X_{mean}}{X_{max}-X_{min}}Xstd=Xmax−XminX−Xmean
Xscaled=Xstd×(max−min)+minX_{scaled}=X_{std}\times(max-min)+minXscaled=Xstd×(max−min)+min ,范围 [−1,1][-1,1][−1,1]
手动化代码演示 实例1:
#!/usr/bin/env python
# -*-coding:utf-8-*-
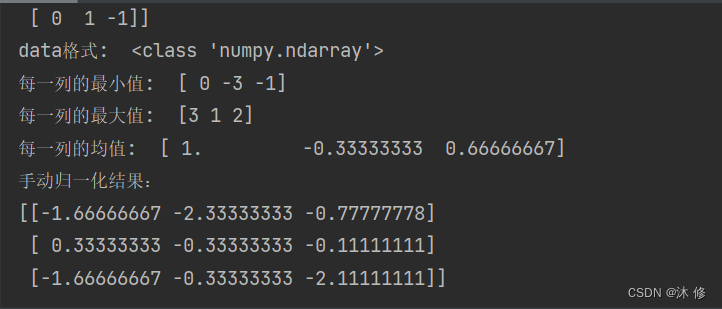
import numpy as npdata = np.array([[ 0, -3, 1],[ 3, 1, 2],[ 0, 1, -1]])print("矩阵: \n",data)
print("data格式: ",type(data))
# 手动归一化
feature_range = [-1,1] # 要映射的区间
print("每一列的最小值: ",data.min(axis=0)) # axis 坐标轴 0 ,从上往下,每一列的最小值
print("每一列的最大值: ",data.max(axis=0)) # axis 坐标轴 0 ,从上往下,每一列的最大值
print("每一列的均值: ",data.mean(axis=0)) # axis 坐标轴 0 ,从上往下,每一列的均值
x_std = (data-data.mean(axis=0))/(data.max(axis=0)-data.min(axis=0)) # axis 坐标轴 0 ,从上往下,列 ,标准化
x_scaled = x_std*(feature_range[1]-feature_range[0]) + feature_range[0]
print('手动归一化结果:\n{}'.format(x_scaled))运行结果 1:
手动化代码演示 实例2:
#!/usr/bin/env python
# -*-coding:utf-8-*-
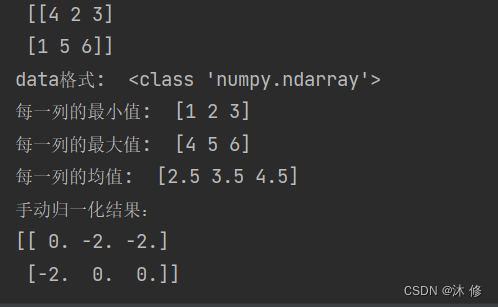
import numpy as npdata = np.array([[4,2,3],[1,5,6]])print("矩阵: \n",data)
print("data格式: ",type(data))
# 手动归一化
feature_range = [-1,1] # 要映射的区间
print("每一列的最小值: ",data.min(axis=0)) # axis 坐标轴 0 ,从上往下,每一列的最小值
print("每一列的最大值: ",data.max(axis=0)) # axis 坐标轴 0 ,从上往下,每一列的最大值
print("每一列的均值: ",data.mean(axis=0)) # axis 坐标轴 0 ,从上往下,每一列的均值
x_std = (data-data.mean(axis=0))/(data.max(axis=0)-data.min(axis=0)) # axis 坐标轴 0 ,从上往下,列 ,标准化
x_scaled = x_std*(feature_range[1]-feature_range[0]) + feature_range[0]
print('手动归一化结果:\n{}'.format(x_scaled))运行结果 2:
3. 小数定标归一化手动化代码演示:
公式:
Xnew=X10kX_{new}=\frac{X}{10^k}Xnew=10kX
- k 取决于 XXX 内的属性取值中的最大绝对值
- 小数定标规范化就是通过移动小数点的位置来进行规范化。
- 小数点移动多少位取决于 XXX 内的属性的取值中的最大绝对值。
这里的 XXX 内的属性代指样本实例的某种属性,比如长度、宽度、数量等。
手动化代码演示:
#!/usr/bin/env python
# -*-coding:utf-8-*-from sklearn import preprocessing
import numpy as np# 初始化数据
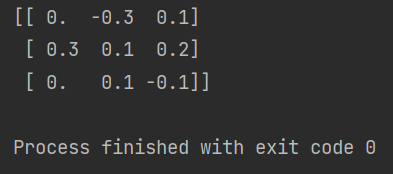
data = np.array([[ 0, -3, 1],[ 3, 1, 2],[ 0, 1, -1]])# 小数定标规范化 # 手动归一化
j = np.ceil(np.log10(np.max(abs(data)))) # abs函数返回一个绝对值的矩阵
scaled_data = data/(10**j) #幂函数运算
print(scaled_data)abs()函数可以对矩阵内的所有数据进行绝对值处理,返回一个只有绝对值的矩阵,np.max() 方法则对绝对值矩阵进行一个最大值处理,找出矩阵内最大的一个值出来,而ceil()方法则是向上取整数,可不是四舍五入那种取整数的方法,而是直接去掉浮点数。
由此得到了以原始数据集内绝对值的最大值为基础的 k 值,利用公式算出了归一化后的新数据。
运行结果:
参考链接:
python abs是什么意思?abs函数有什么用处?
Python numpy.log10用法及代码示例
numpy_ceil函数
4. 零-均值标准化(均值移除)手动与自动化代码演示:
官方文档
sklearn.preprocessing.scale()函数
sklearn.preprocessing.scale(X, axis=0, with_mean=True, with_std=True, copy=True)沿着某个轴(axis)标准化数据集,以均值为中心,以分量为单位方差
axis 的值可以是 0 或 1 , 0 代表了从上往下,列,1代表了从左到右,行
| 参数 | 数据类型 | 意义 |
|---|---|---|
X | {array-like, sparse matrix} | 以此数据为中心缩放 |
axis | int (0 by default) | 沿着计算均值和标准差的轴。如果是0,独立的标准化每个特征,如果是1则标准化每个样本(即行) |
with_mean | boolean, True by default | 如果是True,缩放之前先中心化数据 |
with_std | boolean, True by default | 如果是True,以单位方差法缩放数据(或者等价地,单位标准差) |
copy | boolean, optional, default True | False:原地执行行标准化并避免复制(如果输入已经是一个numpy数组或者scipy.sparse CSC矩阵以及axis是1 —— 行复制) |
公式:
Xnew=X−XmeanXstdX_{new}=\frac{X-X_{mean}}{X_{std}}Xnew=XstdX−Xmean ,均值为 0,方差为 1
手动化与自动化代码对比演示:
#!/usr/bin/env python
# -*-coding:utf-8-*-
import numpy as np
from sklearn import preprocessingdata = np.array([[ 0, -3, 1],[ 3, 1, 2],[ 0, 1, -1]])
print("矩阵: \n",data)
print("data格式: ",type(data))
# 手动归一化
feature_range = [0,1] # 要映射的区间
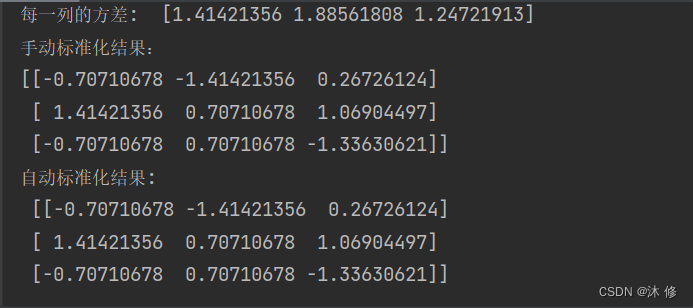
print("每一列的均值: ",data.mean(axis=0)) # axis 坐标轴 0 ,从上往下,每一列的均值
print("每一列的方差: ",data.std(axis=0)) # axis 坐标轴 0 ,从上往下,每一列的均值
x_std = (data-data.mean(axis=0))/(data.std(axis=0)) # axis 坐标轴 0 ,从上往下,列 ,标准化print('手动标准化结果:\n{}'.format(x_std))data = np.array([[ 0, -3, 1],[ 3, 1, 2],[ 0, 1, -1]])# 将数据进行Z-Score规范化 自动标准化
scaled_data = preprocessing.scale(data)
print("自动标准化结果: \n",scaled_data)运行结果:
fit、transform 是什么?
1. MinMaxScaler 归一化接口的 fit 拟合函数
MinMaxScaler 的
fit函数的官方定义:
Compute the minimum and maximum to be used for later scaling.
翻译一下:计算用于进行特征缩放的最大值、最小值
也就是说,通过 fit 函数可以先对需要归一化的数据集进行最大、最小值的计算,至于说最终归一化的结果是多少,对不起,fit 函数到此为止了。
fitn. 拟合
从这里可以知道其实 fit,拟合函数 fit 只能做到将最有价值的最大、最小值,从数据集中提取出来,然后就无法进行下一步的操作 —— 归一化 或 标准化,还有这里提到的仅仅是 MinMaxScaler 模块,这是最大最小归一化模块,要区分下一个要介绍的 StandardScaler 标准化接口的 fit 拟合函数
MinMaxScaler 的 fit 拟合函数代码演示:
#!/usr/bin/env python
# -*-coding:utf-8-*-
import numpy as np
from sklearn.preprocessing import MinMaxScaler# 创建数组
data_rn = np.random.randint(-10, 10, 10).reshape(5, 2) # np模块在-10 到 10 的范围内随机抽取10 个数,并且组成 5行 2 列的矩阵
print("矩阵: \n",data_rn)
# 进行归一化
scaler_mmc = MinMaxScaler()
scaler_mmc_fit = scaler_mmc.fit(data_rn) # 默认 axix=0 按列处理,也就是处理向量
print("提取矩阵中的最大值: ",scaler_mmc_fit.data_max_) # 最大值
print("提取矩阵中的最小值: ",scaler_mmc_fit.data_min_) # 最小值
print("提取矩阵中的极差值: ",scaler_mmc_fit.data_range_) # 极差 最大值减最小值,有两列最大最小值,那么就会有两个极差运行结果:

这是提取每一列的最大值和最小值,第一列最大值是5,第二列最大值是3,第一列最小值是-8,第二列最小值是-4。
2. StandardScaler 标准化接口的 fit 拟合函数
StandardScaler的fit函数的官方定义:
Compute the mean and std to be used for later scaling
翻译一下:计算用于进行特征缩放的均值、标准差
使用StandardScaler模块的fit拟合函数可以对需要标准化的数据集进行均值、标准差的计算
.
StandardScaler 的 fit 拟合函数代码演示:
#!/usr/bin/env python
# -*-coding:utf-8-*-
import numpy as np
from sklearn.preprocessing import StandardScaler# 创建数组
data_rn = np.random.randint(-10, 10, 10).reshape(5, 2) # np模块在-10 到 10 的范围内随机抽取10 个数,并且组成 5行 2 列的矩阵
print("矩阵: \n",data_rn)
# 进行标准化
scaler_ss = StandardScaler()
scaler_ss_fit = scaler_ss.fit(data_rn)
print("均值: ",scaler_ss_fit.mean_) # 均值,默认对列获取均值
print("方差: ",scaler_ss_fit.var_) # 方差,默认对列获取方差运行结果:

可以看出均值和方差都是对每一列进行提取,然后均值和方差都各自得到了两个有价值的均值和方差,所以 fit 拟合函数的存在意义便是如此,从数据中提取有价值的数据出来,为后面的其他数据预处理操作,做准备。
总结一下 fit 的用法:
简单来说,就是求得数据集的均值、方差、最大值、最小值等固有的属性,经常和transform搭配使用
从算法模型的角度上讲,fit 拟合过程可以理解为一个训练过程。
transform 与 fit_transform 函数的理解
官方文档的定义:
MinMaxScaler:Scale features of X according to feature_range.
StandardScaler:Perform standardization by centering and scaling
翻译一下:
MinMaxScaler:根据feature_range进行 XXX 的缩放
StandardScaler:通过居中和缩放执行标准化
也就是说,其实transform才是真正做归一化和标准化的函数,fit拟合函数只是做了前面的准备工作。
从算法模型的角度上讲,transform 过程可以理解为一个转换过程。
用法也很简单,对前面 fit 过的数据集直接进行操作即可
# 归一化
scaler_mmc = MinMaxScaler()
scaler_mmc_fit = scaler_mmc.fit(data_rn) # 默认 axix=0 按列处理,也就是处理向量
scaler_mmc_result = scaler_mmc.transform(data_rn)
# 标准化
scaler_ss = StandardScaler()
scaler_ss_fit = scaler_ss.fit(data_rn)
scaler_ss_result = scaler_ss.transform(data_rn) 最终的结果和直接进行 fit_transform 的结果一致。即:
fit + transform = fit_transform
即
fit_transform是fit和transform的组合,整个过程既包括了训练又包含了转换fit_transform
对数据先拟合fit,找到数据的整体指标,如均值、方差、最大值最小值等,然后对数据集进行转换transform,从而实现数据的标准化、归一化操作。
项目中使用技巧 —— fit_transform 和 transform
了解了 fit、transform 的用法之后,可以再来学习下在项目中使用的小技巧。
项目的数据集一般都会分为 训练集和测试集,训练集用来训练模型,测试集用来验证模型效果。
要想训练的模型在测试集上也能取得很好的得分,不但需要保证训练集数据和测试集数据分布相同,还必须保证对它们进行同样的数据预处理操作。比如:标准化和归一化。
所以一般对于数据集处理上,会直接对训练集进行 拟合+转换,然后直接对测试集 进行转换。
注意了,是用训练集进行拟合,然后对训练集、测试集都用拟合好的”模型“进行转换,一定要明白这个逻辑!!
MinMaxScaler 接口代码演示:
from sklearn.preprocessing import MinMaxScaler scaler_mmc = MinMaxScaler()
# 训练集操作
new_train_x = scaler_mmc.fit_transform(train_x)
# 测试集操作
new_test_x = scaler_mmc.tranform(test_x)StandardScaler 接口代码演示:
from sklearn.preprocessing import StandardScalerscaler_ss = StandardScaler()
# 训练集操作
new_train_x = scaler_ss.fit_transform(train_x)
# 测试集操作
new_test_x = scaler_ss.tranform(test_x)一定要注意,一定要注意,一定要注意:
不能对训练集和测试集都使用 fit_transform,虽然这样对测试集也能正常转换(归一化或标准化),但是两个结果不是在同一个标准下的,具有明显差异。
总结:
- 在用机器学习解决问题时,会将数据集划分成训练集和测试集;
- 我们可以先用
fit_transform()方法处理训练集,再用transform()方法处理测试集。这时,在归一化测试集时,使用的是训练集的统计量,这么做是为了让训练集和测试集更相似。使算法在两者上的表现尽可能相同(这里意味着使用了fit_transform()方法后,相当于使用了fit()方法,然后在使用transform()方法,也就不需要fit()了,因为fit_transform()方法已经将训练集的fit()后的数据,都存储了下来,供transform()方法使用); - 若对测试集使用了
fit_transform()方法,则会用测试集自己的统计量来归一化数据。在测试集上千万不要混用这两个方法,如果在测试集上使用了fit_transform()方法,会导致在测试集上的损失一直比验证集上的大很多; - 还有一个
fit()方法没说,这个是最简单的,它和fit_transform()是相同的,只不过后者会返回转换后的结果,而前者是不会返回的,只会训练转换器; - 首先,如果要想在
fit_transform的过程中查看数据的分布,可以通过分解动作先fit再transform,fit后的结果就包含了数据的分布情况; - 如果不关心数据分布只关心最终的结果可以直接使用
fit_transform一步到位; - 其次,在项目上对训练数据和测试数据需要使用同样的标准进行转换,切记不可分别进行
fit_transform。
参考链接:
做数据处理,你连 fit、transform、fit_transform 都分不清?
对sklearn中transform()和fit_transform()的深入理解
python numpy实现 标准差,方差
【机器学习】数据归一化——MinMaxScaler理解
二、normalize() 方法
normalize 方法的参数:
sklearn.preprocessing.normalize(X, norm='l2', *, axis=1, copy=True, return_norm=False)
XXX: 要规范化的数据
normnormnorm:{‘l1’, ‘l2’, ‘max’},指定范数,默认是矩阵的 2 - 范数,即 l2,但通常而言,常用矩阵的 1- 范数,即 l1 范数,l1归一化:将每个数据除以l1范数(所有数据列的绝对值之和的最大值)
max是矩阵的无穷范数、∣∣A∣∣∝||A||_{\propto}∣∣A∣∣∝
这个方法经常用于确保数据点没有因为特征的基本性质而产生较大的差异,即确保数据处于同一数量级,提高不同特征数据的可比性。
axisaxisaxis:轴,默认是 axis = 1 , 即按样本的行进行计算,用于规范化数据的轴。如果为 1,则独立地对每个样本进行归一化,否则(如果为 0)对每个特征进行归一化,即特征向量。
copycopycopy:bool, default=True
总思路参考链接:
scikit-learn初级
相关文章:

机械学习 - scikit-learn - 数据预处理 - 2
目录关于 scikit-learn 实现规范化的方法详解一、fit_transform 方法1. 最大最小归一化手动化与自动化代码对比演示 1:2. 均值归一化手动化代码演示:3. 小数定标归一化手动化代码演示:4. 零-均值标准化(均值移除)手动与自动化代码演示&#x…...
| 机考必刷)
华为OD机试题 - 最长连续交替方波信号(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:最长连续交替方波信号题目输入输出示例一输入输出Code解题思路版…...
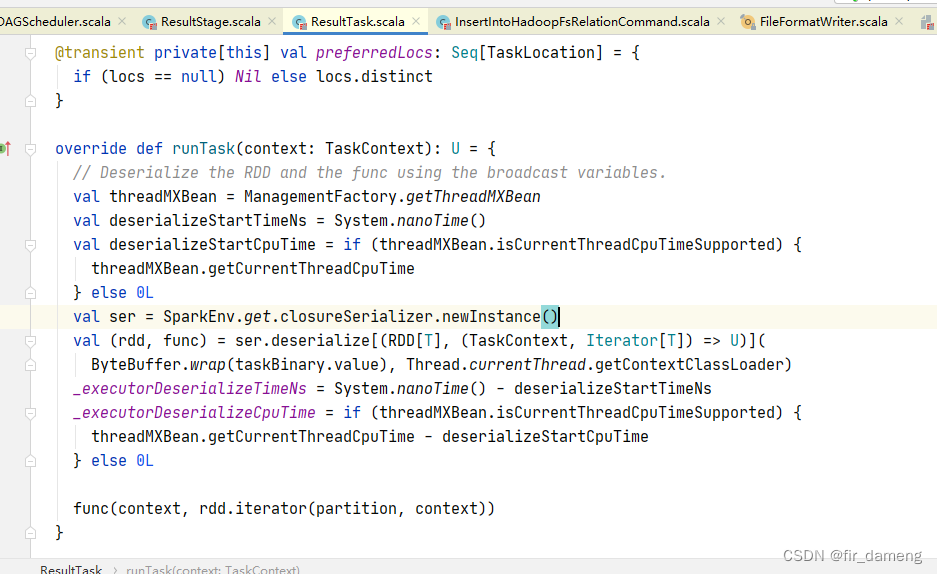
executor行为相关Spark sql参数源码分析
0、前言 参数名和默认值spark.default.parallelismDefault number of partitions in RDDsspark.executor.cores1 in YARN mode 一般默认值spark.files.maxPartitionBytes134217728(128M)spark.files.openCostInBytes4194304 (4 MiB)spark.hadoop.mapreduce.fileoutputcommitte…...
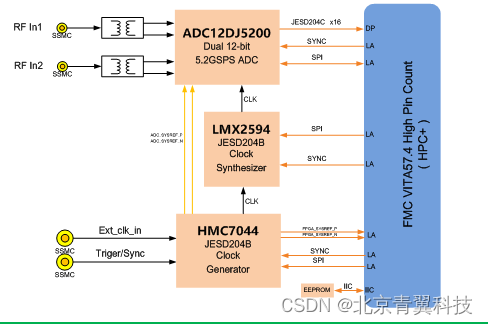
双通道5.2GSPS(或单通道10.4GSPS)射频采样FMC+模块
概述 FMC140是一款具有缓冲模拟输入的低功耗、12位、双通道(5.2GSPS/通道)、单通道10.4GSPS、射频采样ADC模块,该板卡为FMC标准,符合VITA57.1规范,该模块可以作为一个理想的IO单元耦合至FPGA前端,8通道的JE…...

理解java反射
是什么Java反射是Java编程语言的一个功能,它允许程序在运行时(而不是编译时)检查、访问和修改类、对象和方法的属性和行为。使用反射创建对象相比直接创建对象有什么优点使用反射创建对象相比直接创建对象的主要优点是灵活性和可扩展性。当我…...

EasyRcovery16免费的电脑照片数据恢复软件
电脑作为一种重要的数据储存设备,其中保存着大量的文档,邮件,视频,音频和照片。那么,如果电脑照片被删除了怎么办?今天小编给大家介绍,误删除的照片从哪里可以找回来,误删除的照片如…...
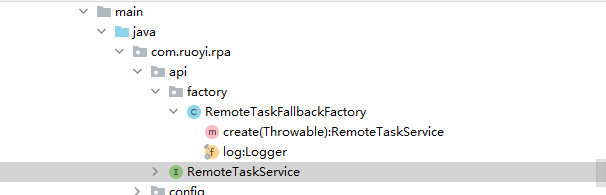
若依微服务版在定时任务里面跨模块调用服务
第一步 在被调用的模块中添加代理 RemoteTaskFallbackFactory.java: package com.ruoyi.rpa.api.factory;import com.ruoyi.common.core.domain.R; import com.ruoyi.rpa.api.RemoteTaskService; import org.slf4j.Logger; import org.slf4j.LoggerFactory; import org.springf…...

SpringMVC简单配置
1、pom.xml配置 <dependencies><dependency><groupId>org.springframework</groupId><artifactId>spring-webmvc</artifactId><version>5.1.12.RELEASE</version></dependency></dependencies><build><…...

xcat快速入门工作流程指南
目录一、快速入门指南一、先决条件二、准备管理节点xcatmn.mydomain.com三、第1阶段:添加你的第一个节点并且用带外BMC接口控制它四、第 2 阶段 预配节点并使用并行 shell 对其进行管理二:工作流程指南1. 查找 xCAT 管理节点的服务器2. 在所选服务器上安…...

C++回顾(十九)—— 容器string
19.1 string概述 1、string是STL的字符串类型,通常用来表示字符串。而在使用string之前,字符串通常是 用char * 表示的。string 与char * 都可以用来表示字符串,那么二者有什么区别呢。 2、string和 char * 的比较 (1)…...

Hadoop入门
数据分析与企业数据分析方向 数据是什么 数据是指对可观事件进行记录并可以鉴别的符号,是对客观事物的性质、状态以及相互关系等进行记载的物理符号或这些物理符号的组合,它是可以识别的、抽象的符号。 他不仅指狭义上的数字,还可以是具有一…...

高校如何通过校企合作/实验室建设来提高大数据人工智能学生就业质量
高校人才培养应该如何结合市场需求进行相关专业设置和就业引导,一直是高校就业工作的讨论热点。亘古不变的原则是,高校设置不能脱离市场需求太远,最佳的结合方式是,高校具有前瞻性,能领先市场一步,培养未来…...

提升学习 Prompt 总结
NLP现有的四个阶段: 完全有监督机器学习完全有监督深度学习预训练:预训练 -> 微调 -> 预测提示学习:预训练 -> 提示 -> 预测 阶段1,word的本质是特征,即特征的选取、衍生、侧重上的针对性工程。 阶段2&…...
)
JavaScript学习笔记(2.0)
BOM--(browser object model) 获取浏览器窗口尺寸 获取可视窗口高度:window.innerWidth 获取可视窗口高度:window.innerHeight 浏览器弹出层 提示框:window.alert(提示信息) 询问框:window.confirm(提示信息) 输…...

直击2023云南移动生态合作伙伴大会,聚焦云南移动的“价值裂变”
作者 | 曾响铃 文 | 响铃说 2023年3月2日下午,云南移动生态合作伙伴大会在昆明召开。云南移动党委书记,总经理葛松海在大会上提到“2023年,云南移动将重点在‘做大平台及生态级新产品,做优渠道转型新动能,做强合作新…...

STM32F1开发实例-振动传感器(机械)
振动(敲击)传感器 振动无处不在,有声音就有振动,哒哒的脚步是匆匆的过客,沙沙的夜雨是暗夜的忧伤。那你知道理科工程男是如何理解振动的吗?今天我们就来讲一讲本节的主角:最简单的机械式振动传感器。 下图即为振动传…...
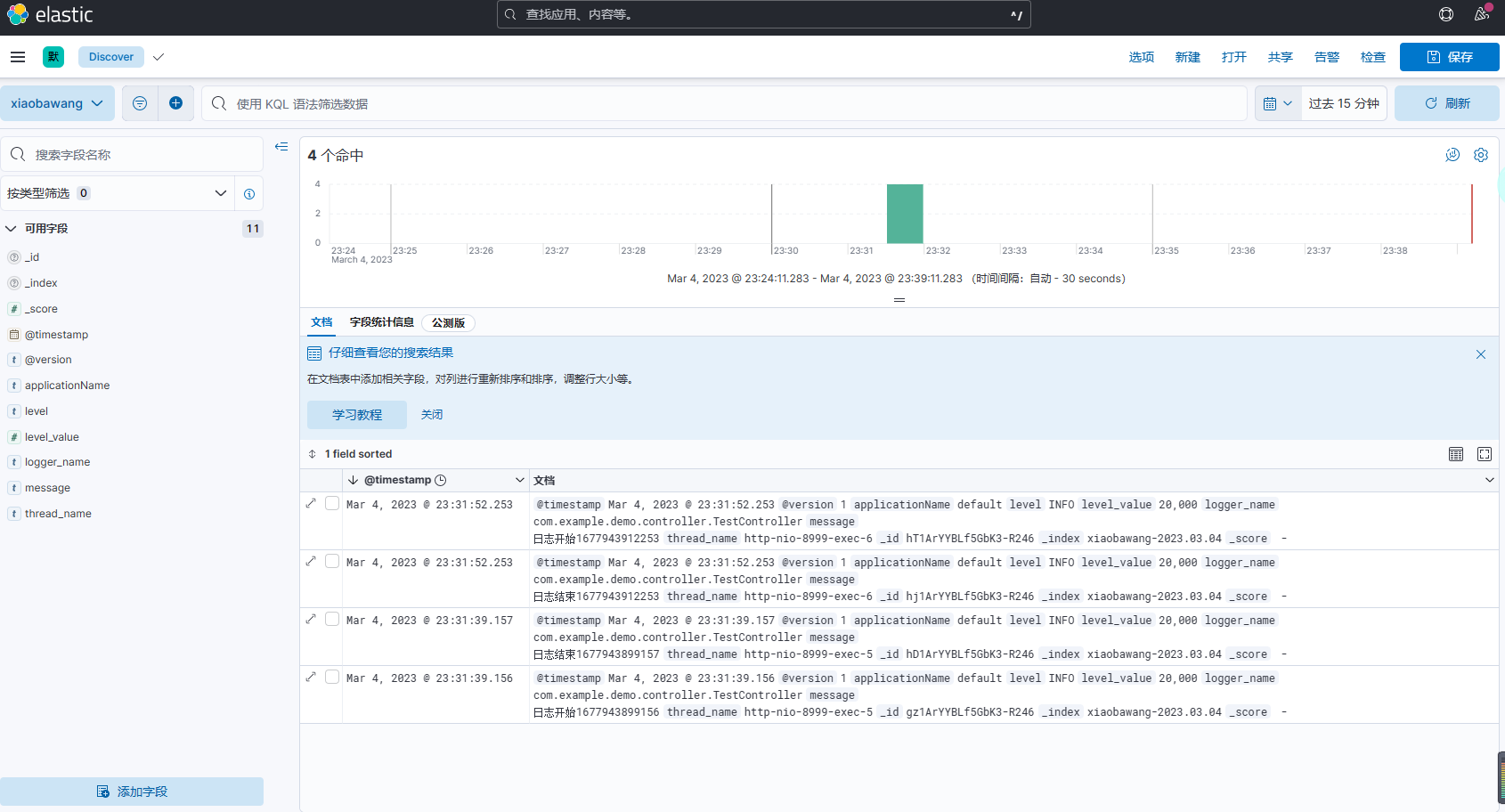
2023最新ELK日志平台(elasticsearch+logstash+kibana)搭建
去年公司由于不断发展,内部自研系统越来越多,所以后来搭建了一个日志收集平台,并将日志收集功能以二方包形式引入自研系统,避免每个自研系统都要建立一套自己的日志模块,节约了开发时间,管理起来也更加容易…...

2023-3-10 刷题情况
打家劫舍 IV 题目描述 沿街有一排连续的房屋。每间房屋内都藏有一定的现金。现在有一位小偷计划从这些房屋中窃取现金。 由于相邻的房屋装有相互连通的防盗系统,所以小偷 不会窃取相邻的房屋 。 小偷的 窃取能力 定义为他在窃取过程中能从单间房屋中窃取的 最大…...

如何建立一个成功的MES?
制造执行系统(MES)是一种为制造业企业提供实时生产过程控制、管理和监视的信息系统。一个成功的MES系统可以帮助企业提高生产效率,降低成本,提高产品质量,提高客户满意度等。下面是一些关键步骤来建立一个成功的MES系统…...

Kafka生产者幂等性/事务
Kafka生产者幂等性/事务幂等性事务Kafka 消息交付可靠性保障: Kafka 默认是:至少一次最多一次 (at most once) : 消息可能会丢失,但绝不会被重复发送至少一次 (at least once) : 消息不会丢失,但有可能被重复发送精确一次 (exact…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
