K-Means 算法详解
K-Means 是一种常用的无监督学习算法,广泛应用于数据聚类分析。本文将详细讲解 K-Means 算法的原理、步骤、公式以及 Python 实现,帮助你深入理解这一经典算法。
什么是 K-Means 算法?
K-Means 算法是一种基于原型的聚类算法,其目标是将数据集分成K个簇(clusters),使得同一簇内的数据点尽可能相似,不同簇之间的数据点尽可能不同。每个簇由其中心(即质心,centroid)表示。
K-Means 算法的步骤
K-Means 算法的主要步骤如下:
- 初始化:随机选择 K个数据点作为初始质心。
- 分配簇:将每个数据点分配到距离其最近的质心对应的簇。
- 更新质心:计算每个簇的质心,即簇内所有数据点的平均值。
- 重复步骤 2 和 3:直到质心不再发生变化(或变化很小),或者达到预设的迭代次数。
详细步骤解释
-
初始化:
- 从数据集中随机选择K 个点作为初始质心。这些质心可以是数据集中的实际点,也可以是随机生成的点。
-
分配簇:
- 计算每个数据点到所有质心的距离(通常使用欧氏距离)。对于数据点 ( x i ) \ (x_i ) (xi) 和质心 ( μ j ) (\mu_j) (μj),欧氏距离计算公式为:
d ( x i , μ j ) = ∑ m = 1 M ( x i m − μ j m ) 2 \ d(x_i, \mu_j) = \sqrt{\sum_{m=1}^M (x_{im} - \mu_{jm})^2} \ d(xi,μj)=m=1∑M(xim−μjm)2 - 将每个数据点分配到距离其最近的质心对应的簇,即:
C i = { x p : ∥ x p − μ i ∥ ≤ ∥ x p − μ j ∥ , ∀ j , 1 ≤ j ≤ k } \ C_i = \{ x_p : \| x_p - \mu_i \| \leq \| x_p - \mu_j \|, \forall j, 1 \leq j \leq k \} \ Ci={xp:∥xp−μi∥≤∥xp−μj∥,∀j,1≤j≤k}
- 计算每个数据点到所有质心的距离(通常使用欧氏距离)。对于数据点 ( x i ) \ (x_i ) (xi) 和质心 ( μ j ) (\mu_j) (μj),欧氏距离计算公式为:
-
更新质心:
- 对每个簇 ( C i ) \ ( C_i ) (Ci),计算簇内所有数据点的平均值,并将该平均值作为新的质心。新的质心计算公式为:
μ i = 1 ∣ C i ∣ ∑ x j ∈ C i x j \ \mu_i = \frac{1}{|C_i|} \sum_{x_j \in C_i} x_j \ μi=∣Ci∣1xj∈Ci∑xj
- 对每个簇 ( C i ) \ ( C_i ) (Ci),计算簇内所有数据点的平均值,并将该平均值作为新的质心。新的质心计算公式为:
-
重复:
- 重复分配簇和更新质心的步骤,直到质心位置不再发生变化或达到最大迭代次数。
K-Means 算法的优化目标
K-Means 算法的优化目标是最小化所有数据点到其所属簇质心的距离平方和。优化目标函数可以表示为:
J = ∑ i = 1 k ∑ x j ∈ C i ∥ x j − μ i ∥ 2 \ J = \sum_{i=1}^k \sum_{x_j \in C_i} \| x_j - \mu_i \|^2 \ J=i=1∑kxj∈Ci∑∥xj−μi∥2
该目标函数也称为聚类内的总平方误差(Total Within-Cluster Sum of Squares,简称 TSS)。
K-Means 算法的优缺点
优点
- 简单易懂:K-Means 算法原理简单,容易实现。
- 速度快:算法收敛速度快,适合处理大规模数据集。
- 适用范围广:在许多实际问题中表现良好。
缺点
- 选择 ( k ) 值的困难:需要预先指定簇的数量 ( k ),而合适的 ( k ) 值通常不易确定。
- 对初始值敏感:初始质心的选择会影响最终结果,可能陷入局部最优解。
- 对异常值敏感:异常值可能会显著影响质心的位置。
K-Means 算法的 Python 实现
下面通过 Python 代码实现 K-Means 算法,并以一个示例数据集展示其应用。
导入库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeansplt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
生成示例数据集
# 生成示例数据集
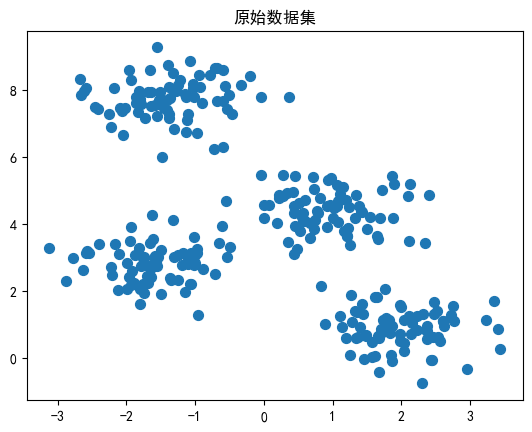
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.show()
应用 K-Means 算法
# 应用 K-Means 算法
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)# 可视化聚类结果
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75, marker='x')
plt.show()
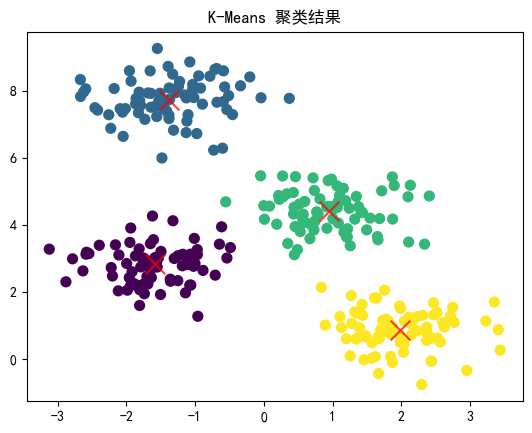
结果解释
在上面的示例中,我们生成了一个有 4 个簇的示例数据集,并使用 K-Means 算法对其进行聚类。最终,我们通过可视化展示了聚类结果以及每个簇的质心。
总结
K-Means 算法是一种简单而有效的聚类算法,广泛应用于各种数据分析和机器学习任务中。本文详细介绍了 K-Means 算法的原理、步骤、公式以及 Python 实现。虽然 K-Means 算法有一些缺点,但通过合理选择参数和预处理数据,可以在许多实际应用中取得良好的效果。希望本文能帮助你更好地理解和应用 K-Means 算法。
相关文章:

K-Means 算法详解
K-Means 是一种常用的无监督学习算法,广泛应用于数据聚类分析。本文将详细讲解 K-Means 算法的原理、步骤、公式以及 Python 实现,帮助你深入理解这一经典算法。 什么是 K-Means 算法? K-Means 算法是一种基于原型的聚类算法,其…...

【DIY飞控板PX4移植】BARO模块BMP388气压计的PCB硬件设计和PX4驱动配置
BARO模块BMP388气压计的PCB硬件设计和PX4驱动配置 BMP388简介硬件设计封装原理图PCB设计引脚选择问题 PX4驱动配置飞控板的配置文件夹结构default.px4board文件nuttx-config/nsh/defconfig文件nuttx-config/include/board.h文件src/board_config.h文件src/i2c.cpp文件init/rc.b…...
Flutter框架高阶——Window应用程序设置窗体窗口背景完全透明
文章目录 1.修改 main.cpp1)C 与 Win32 API2)EnableTransparency()3)中文注释 2.编写 Flutter 代码1)bitsdojo_window2)window_manager3)区别对比4)同时使用(1)设置初始化…...

HJ39判断两个IP是否属于同一子网
提示:文章 文章目录 前言一、背景二、 2.1 2.2 总结 前言 HJ39判断两个IP是否属于同一子网 一、 代码: 第一版代码没有对掩码网络号进行处理。一开始对非法字段的理解就是value大于255。然后执行示例, 254.255.0.0 85.122.52.249 10.57.…...
opencv学习笔记(2)
设置鼠标回调函数 setMouseCallback(winname, callback, userdata) winname:窗口名字 callback:回调函数 userdata:传回callback中 callback(event, x, y, flags,userdata) event:鼠标事件 x: 鼠标的x坐标 y: 鼠标的y坐标 flags:鼠标键和组合键 userdata:setMouseCallback传回…...

分享vs code十大好用的插件
1.Chinese (Simplified) (简体中文) Language Pack for Visual Studio Code 将 VS Code 界面改成简体中文。 2.PDF Viewer 在VS Code 中打开 PDF文件。 3.TODO Highlight 这个扩展会突出显示您的待办事项注释,并提醒存在未完成的注释或任务。 该扩展附带了内…...

MySQL支持哪些特殊字符
MySQL支持多种特殊字符,这些字符在SQL语句中具有特定的含义,需要在使用时特别注意。以下是一些MySQL中的特殊字符及其相关信息: 引号: 单引号():用于定义字符串。如果字符串中包含单引号本身&…...

c语言中的宏是什么?
宏的定义及用途 C语言中的宏是一种预处理指令,它允许程序员定义一个名称,该名称可以代表一段代码或一个值。宏的主要用途是简化代码的编写,提高代码的可读性和可维护性,以及实现代码的重复利用。 宏的定义使用#define指令&#…...

采购信息记录标准编码范围维护以及如何开发获取编码范围
上图是配置的点,在这里可以获取到对应的编号范围以及对象名称 下面的话是官方就如何取编号的技术文档 SAP Help Portal...
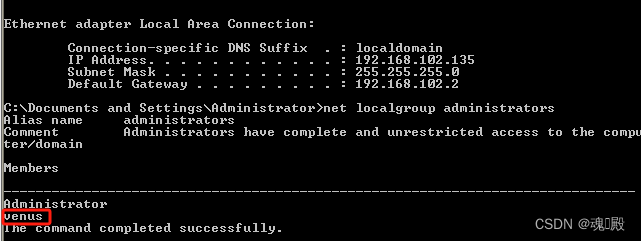
渗透测试基础(四) MS08-067 漏洞攻击
1. 漏洞介绍 漏洞描述 Microsoft Windows Server服务RPC请求缓冲区溢出漏洞Windows的Server服务在处理特质RPC请求时存在缓冲区溢出漏洞,远程攻击者可以通过发送恶意的RPC请求触发这个溢出,导致完全入侵用户系统,以SYSTEM权限执行任意指令。…...

vmware 虚拟机保留数据扩展C盘
1,在默认安装系统的时候,VMWARE一般给C盘50G,很多人想着够用了,但是后面慢慢的安装各种大型软件,游戏,才发现,悔时已晚。 2,有很多人虚拟机其实就是拿来游戏多开,但是当…...

vscode cmake c++ include 设置
在这里设置编译器路径,include路径等等。 一个奇怪的现象是同一项目放在VS中可以cmake生成,并正常运行,但是放在VSCODE中cmake生成时会报错,如iostream、limits等头文件找不到。当在VS中运行执行完成调试后,在运行VSC…...
)
2024-06-19 高等数学(统计学和概率论-高等工科数学)
学习数学时,有效的笔记方法可以帮助你更好地理解和记忆概念、公式和解题技巧。下面是一个数学笔记的基本模本,你可以根据自己的需求进行调整: 1. **标题**:写上日期和课程名称,例如“2024-06-19 高等数学”。 2. **课…...
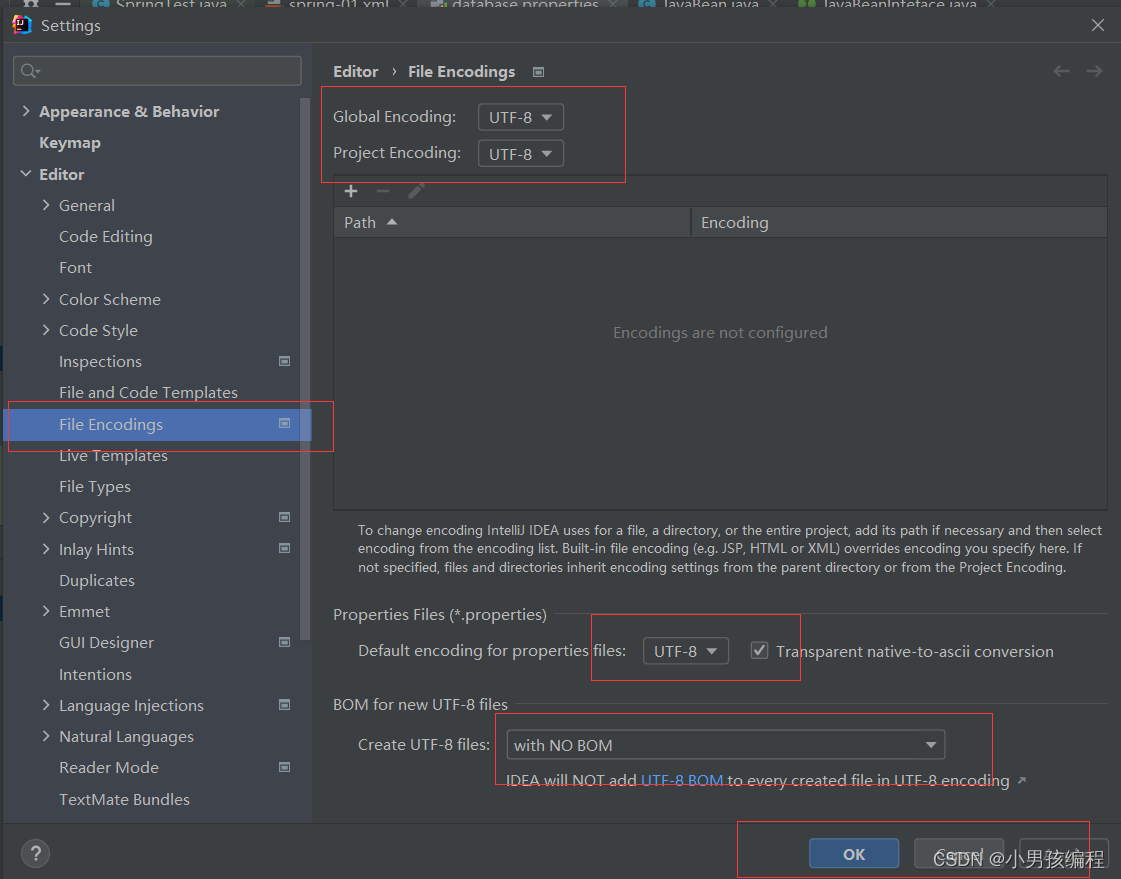
idea 创建properties文件,解决乱码
设置properties文件编码 点击file->Settings File Encodings->设置utf-8 重新创建.properties文件才生效...
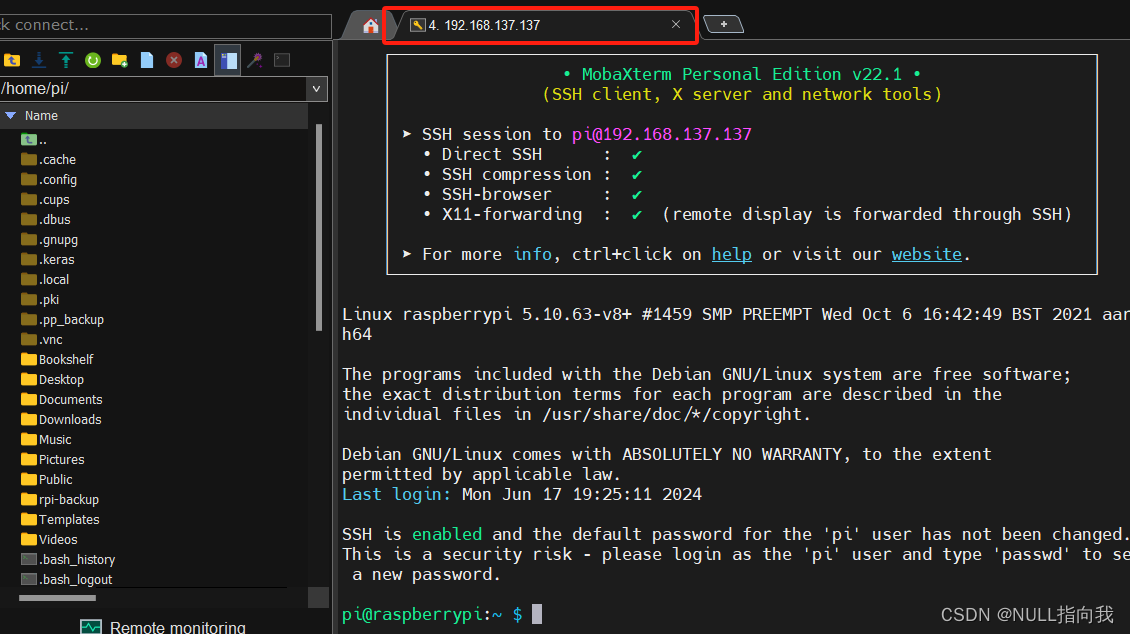
树莓派4B学习笔记11:PC端网线SSH连接树莓派_网线连接请求超时问题解决
今日继续学习树莓派4B 4G:(Raspberry Pi,简称RPi或RasPi) 本人所用树莓派4B 装载的系统与版本如下: 版本可用命令 (lsb_release -a) 查询: Opencv 版本是4.5.1: 今日学习使用网线连接树莓派,网线可以提供更…...

适合营销的叙事可视化
背景 数据可视化与数据故事化的差异和相似点,以及它们如何协同工作,将你的数据转化为清晰、简洁、可操作的信息,以便您的组织使用。 什么是数据可视化? 数据可视化通过图像传达信息——这是你所收集数据的视觉表示。通过提供原…...
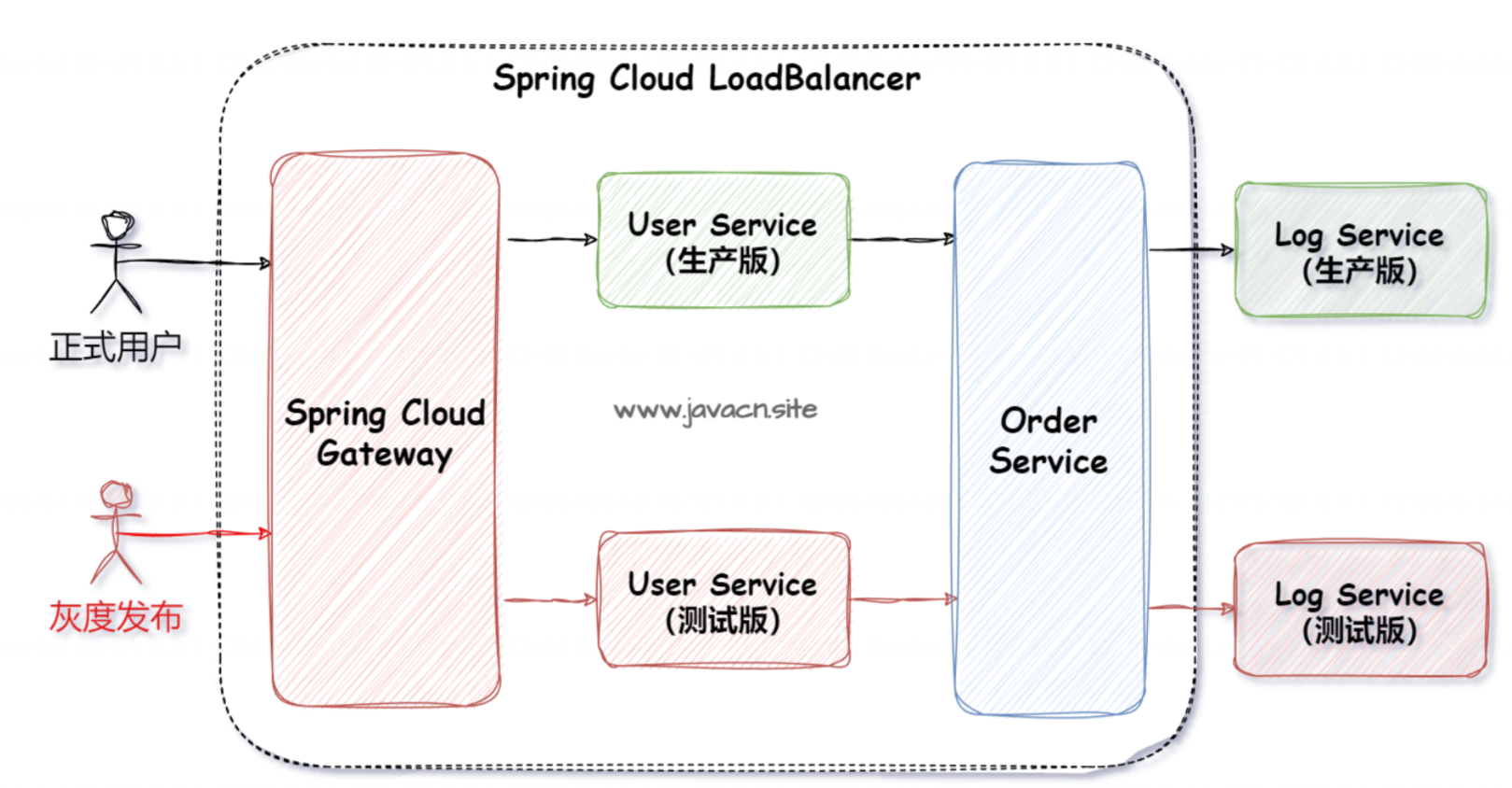
Spring Cloud全家桶(上)【Nacos、OpenFeign、LoadBalancer、GateWay、金丝雀灰色发布】
0.零基础入门微服务实战课 1.微服务和 Spring Cloud1.1 什么是微服务?1.2 什么是 Spring Cloud?1.3 微服务 VS Spring Cloud 2.为什么要学微服务?3.Spring Cloud 组件介绍1.什么是 Nacos?1.1 Nacos 功能1.1.1 配置中心1.1.2 注册中心 1.2 Na…...

GPRS与4G网络:技术差异与应用选择
在移动通信的发展历程中,GPRS(General Packet Radio Service)和4G(Fourth-Generation)技术都扮演着举足轻重的角色。虽然两者都旨在提供无线数据传输服务,但在数据传输速率、延迟和覆盖范围等方面ÿ…...

【Spring】1. Maven项目管理
📚博客主页:爱敲代码的小杨. ✨专栏:《Java SE语法》 | 《数据结构与算法》 | 《C生万物》 |《MySQL探索之旅》 |《Web世界探险家》 ❤️感谢大家点赞👍🏻收藏⭐评论✍🏻,您的三连就是我持续更…...
工业制造领涉及的8大常见管理系统,如mes、scada、aps、wms等
在工业生产和制造领域有一些常见的管理系统,很多小伙伴分不清,这次大美B端工场带领大家了解清楚。 MES(Manufacturing Execution System,制造执行系统): MES是一种用于监控、控制和优化生产过程的软件系统…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
