【抽代复习笔记】20-群(十四):定理6的补充证明及三道循环置换例题
例1:找出S3中所有不能和(123)交换的元。
解:因为 (123)(1) = (1)(123) = (123),(123)(132) = (132)(123) = (1),所以(1)、(132)和(123)均可以交换;
而(12)(123) = (23),(123)(12) = (13),故 (12)(123) ≠ (123)(12),因此(12)和(123)不可交换;
同理,(13),(23)也与(123)不可交换。
因此,S3中所有不能和(123)交换的元有(12),(13),(23)。
定理9:Sn中每一个元都可以写为(12),(13),...,(1n)这n-1个2-循环置换中若干个的乘积。
【证明补充:定理6(见上一篇文章):两个不相交的循环置换的乘积可交换。】
证:设A = {1,2,...,n},Sn是n次对称群。
σ = (r1r2...rn),r = (t1t2...tl)是Sn中不相交的循环置换,即:
{r1,r2,...,rk} ∩ {t1,t2,...,tl} = ∅,将σ和r视为映射,证σr = rσ——
对任意i∈A,
①若i∈{r1,r2,...,rk},则i∉{t1,t2,...,tl},
σ(i) = rm,则rm∉{t1,t2,...,tl},从而:
(σ o r)(i) = σ(r(i)) = σ(i) = rm,(r o σ)(i) = r(σ(i)) = r(rm) = rm,
因此 (σ o r)(i) = (r o σ)(i) = rm,即σr = rσ;
②若i∈{t1,t2,...,tl},即i∉{r1,r2,...,rk},
令 r(i) = tn∉{r1,r2,...,rk},从而:
(σ o r)(i) = σ(r(i)) = σ(tn) = tn,(r o σ)(i) = r(σ(i)) = r(i) = tn,
因此(σ o r)(i) = (r o σ)(i) = tn,即σr = rσ;
③若i∉{t1,t2,...,tl,r1,r2,...,rk},则σ(i) = i = r(i),从而:
(σ o r)(i) = σ(r(i)) = σ(i) = i,(r o σ)(i) = r(σ(i)) = r(i) = i,
因此(σ o r)(i) = (r o σ)(i) = i,即σr = rσ。
综上所述,不管是哪种情况,都有σr = rσ,由此得证两个不相交的循环置换的乘积可交换。
例2:证明,一个k-循环置换的阶为k。
证:设σ = (i1i2...ik)是Sn上的一个k-循环,因为:
σ(i1) = i2,σ(i2) = σ(σ(i1)) = σ(i1)^2 = i3,σ(i3) = σ(σ(i2)) = σ(i1)^3 = i4,……,σ(i1)^(k-1) = ik,σ(i1)^k = σ(ik) = i1,
因此σ(i1)^k = i1,但σ(i1)^l ≠ i1(0<l<k),
类似地,对于任意j∈{2,3,k-1,k},都有σ(ij)^k = ij,且σ(ij)^l ≠ ij(l<k),
由此得σ^k = (1),也就是|σ| = k。
例3:证明,Sn中每一个元都可写为(12),(13),……,(1n)中若干个的乘积。
证:设σ是Sn中任一k-循环,
(1)若1在σ中出现,则:
σ = (1 i1 i2 …… ik-1) = (1 ik-1)(1 ik-2)……(1 i1);
(2)若1没在σ中出现,则:
σ = (i1 i2 …… ik) = (1 i1)(1 i1 i2 …… ik) = (1 i1)(1 ik)(1 ik-1)……(1 i1)
综上,Sn中每一个元都可写为(12),(13),……,(1n)中若干个的乘积,命题得证。
(待续……)
相关文章:
:定理6的补充证明及三道循环置换例题)
【抽代复习笔记】20-群(十四):定理6的补充证明及三道循环置换例题
例1:找出S3中所有不能和(123)交换的元。 解:因为 (123)(1) (1)(123) (123),(123)(132) (132)(123) (1),所以(1)、(132)和(123)均可以交换; 而(12)(123) (23),(123)(12) (13),故 (12)(12…...
【单片机毕业设计选题24018】-基于STM32和阿里云的农业大棚系统
系统功能: 系统分为手动和自动模式,上电默认为自动模式,自动模式下系统根据采集到的传感器值 自动控制,温度过低后自动开启加热,湿度过高后自动开启通风,光照过低后自动开启补 光,水位过低后自动开启水泵…...

【计算机毕业设计】206校园顺路代送微信小程序
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

9、PHP 实现调整数组顺序使奇数位于偶数前面
题目: 调整数组顺序使奇数位于偶数前面 描述: 输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分, 所有的偶数位于位于数组的后半部分,并保证奇数和奇数ÿ…...
iOS开发工具-网络封包分析工具Charles
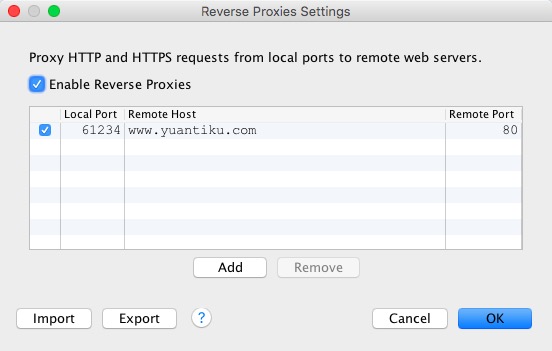
一、Charles简介 Charles 是在 Mac 下常用的网络封包截取工具,在做 移动开发时,我们为了调试与服务器端的网络通讯协议,常常需要截取网络封包来分析。 Charles 通过将自己设置成系统的网络访问代理服务器,使得所有的网络访问请求…...

7、PHP 实现矩形覆盖
题目: 矩形覆盖 描述: 我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。 请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法? <?php function rectCover($number) {$prePreNum 1;$preNum 2;$temp 0;i…...
鸿蒙开发通信与连接:【@ohos.wifiext (WLAN)】
WLAN 说明: 本模块首批接口从API version 8开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。 该文档中的接口只供非通用类型产品使用,如路由器等,对于常规类型产品,不应该使用这些接口。 导入模块 …...

Ps:脚本事件管理器
Ps菜单:文件/脚本/脚本事件管理器 Scripts/Script Events Manager 脚本事件管理器 Script Events Manager允许用户将特定的事件(如打开、存储或导出文件)与 JavaScript 脚本或 Photoshop 动作关联起来,以便在这些事件发生时自动触…...

redis哨兵模式下业务代码连接实现
目录 一:背景 二:实现过程 三:总结 一:背景 在哨兵模式下,真实的redis服务地址由一个固定ip转变为可以变化的ip,这样我们业务代码在连接redis的时候,就需要判断哪个主redis服务地址,哪个是从…...
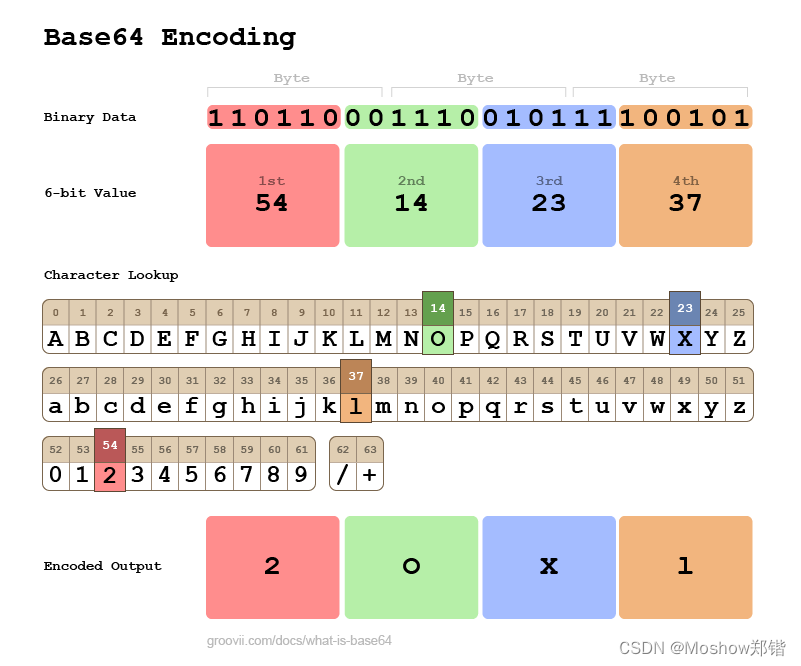
Java中将文件转换为Base64编码的字节码
在Java中,将文件转换为Base64编码的字节码通常涉及以下步骤: 读取文件内容到字节数组。使用java.util.Base64类对字节数组进行编码。 下面是一个简单的Java示例代码,演示如何实现这个过程: import java.io.File; import java.io…...

【C++高阶】探索STL的瑰宝 map与set:高效数据结构的奥秘与技巧
📝个人主页🌹:Eternity._ ⏩收录专栏⏪:C “ 登神长阶 ” 🤡往期回顾🤡:初步了解 二叉搜索树 🌹🌹期待您的关注 🌹🌹 ❀map与set 📒1.…...
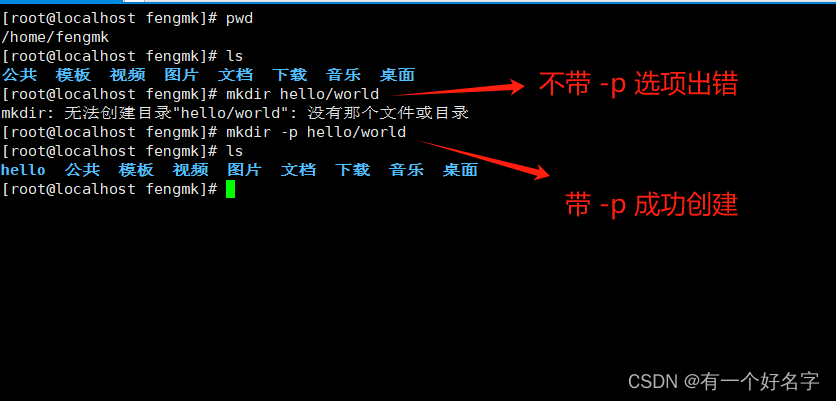
cd 命令特殊路径符 mkdir命令
cd 特殊路径符 cd . 表示当前目录,比如 cd ./Desktop表示切换到当前目录下的Desktop目录内,和 cd Desktop效果一致。cd … 表示上一级目录,比如 cd … 即可切换到上一级目录,cd…/…切换到上二级目录。cd ~ 表示 HOME 目录&#…...

Mongodb UPDATE, 使用$position指定向数组中插入新元素的位置
学习mongodb,体会mongodb的每一个使用细节,欢迎阅读威赞的文章。这是威赞发布的第72篇mongodb技术文章,欢迎浏览本专栏威赞发布的其他文章。如果您认为我的文章对您有帮助或者解决您的问题,欢迎在文章下面点个赞,或者关…...
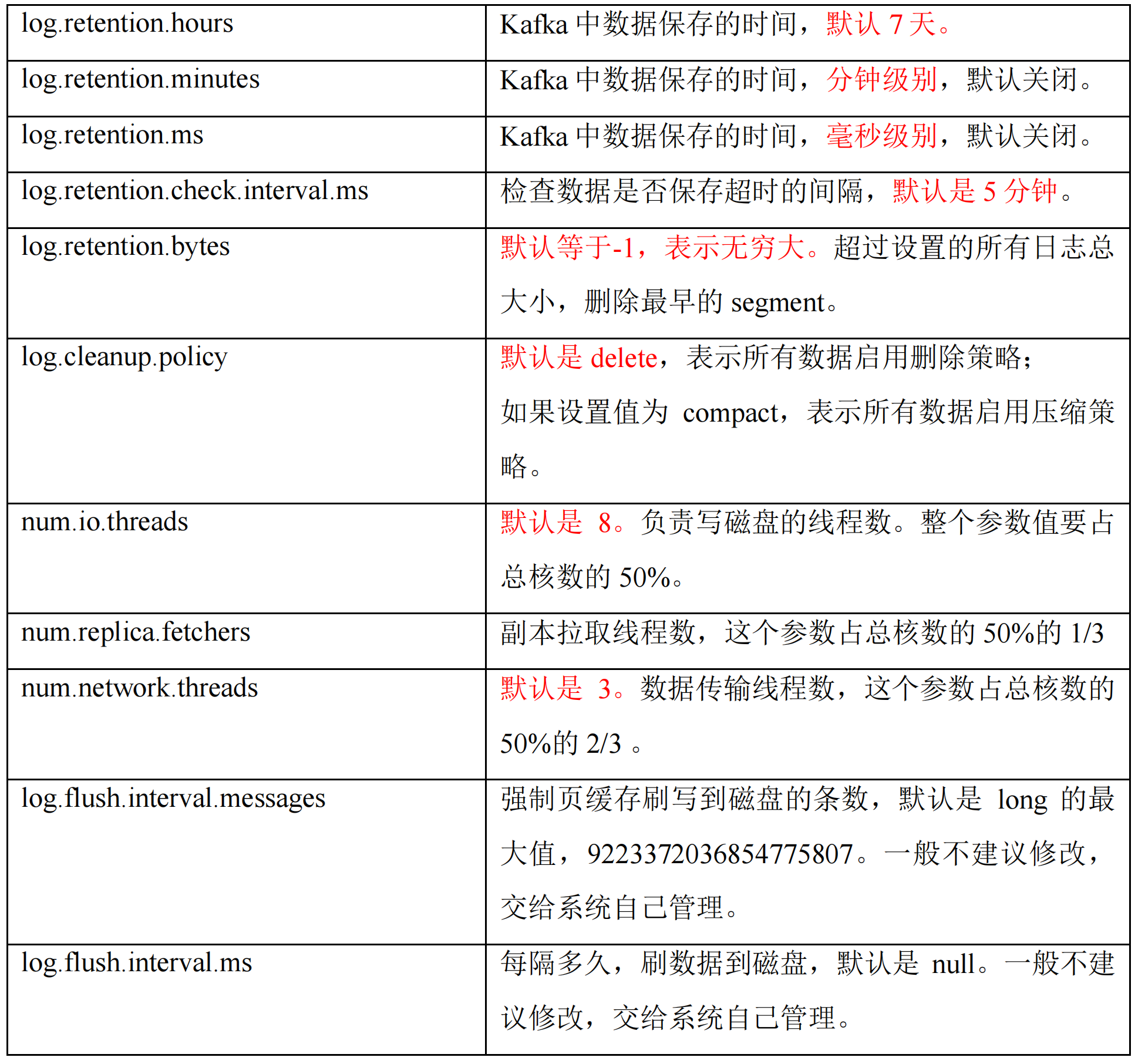
【Kafka】Kafka Broker工作流程、节点服役与退役、副本、文件存储、高效读写数据-08
【Kafka】Kafka Broker工作流程、节点服役与退役、副本、文件存储、高效读写数据 1. Kafka Broker 工作流程1.1 Zookeeper 存储的 Kafka 信息1.2 Kafka Broker总体工作流程1.2.1 Controller介绍 1.3 Broker 重要参数 2. 节点服役与退役3. Kafka副本 1. Kafka Broker 工作流程 …...
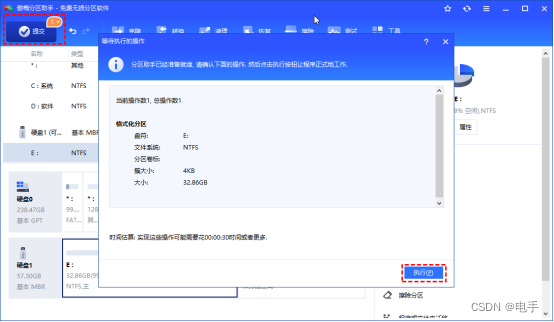
如何恢复未格式化分区数据?看这里!
什么是未格式化分区? 未格式化或RAW文件系统的分区无法被Windows操作系统识别和挂载,因此,Windows会提示你进行格式化以创建新的文件系统。注意,不要进行格式化。通常,文件系统变为未格式化或RAW会出现以下常见错误消…...

通过“BOSS”精通比特币,深入认识私钥、账户和钱包
来源:币界原创 作者:636Marx 无论当今数字货币技术如何发展,认识区块链技术幕后的关键机制至关重要。无论您是新手还是经验丰富的数字货币从业者,掌握钱包地址、公钥和私钥的复杂性都有无可替代重要性。进入 BOSS Wallet,这是一款尖端的 Web…...

进程与线程的区别
进程(Process) 1:进程是操作系统分配资源的基本单位 2:每个进程都有自己独立的虚拟地址空间,虚拟地址空间映射真实物理地址 3:进程之间相互隔离,某一个进程的崩溃不会影响到其它进程 4&…...
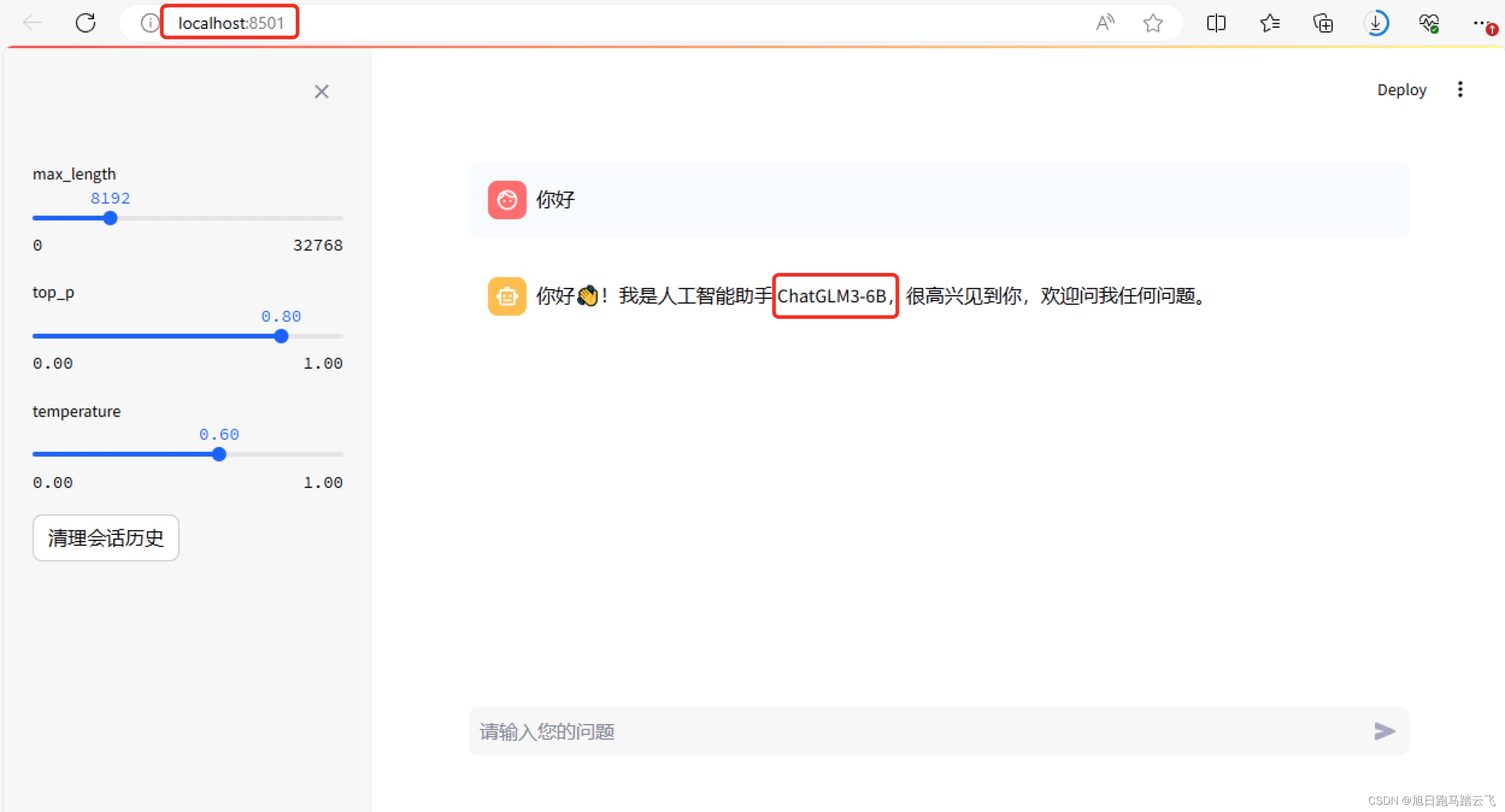
【AI基础】第五步:纯天然保姆喂饭级-安装并运行chatglm3-6b
类似于 【AI基础】第三步:纯天然保姆喂饭级-安装并运行chatglm2-6b,有一些细节不一样。 此系列文章列表: 【AI基础】概览 【AI基础】第一步:安装python开发环境-windows篇_下载安装ai环境python 【AI基础】第一步:安装…...

【学习笔记】Elastic-Job和Quartz 实现企业级定时任务
Elastic-Job和Quartz 实现企业级定时任务 知识拆解框架整合Java高级玩法定时任务案例 第1章 课程介绍 课程的总体介绍,定时任务的应用场景和发展趋势,以及分布式走时任务的介绍 1-1、导学 1-2、为什么学习定时任务 1-3、定时任务技术发展趋势 1-4、主…...

舒适佩戴,享受沉浸式音乐体验,西圣AVA2耳机体验
平时不管是听音乐,还是打电话,戴上一副耳机都可以让我们获得更好的隐私性,并且在公共场所,比如办公室、车厢里,也可以获得属于自己的空间。现在市面上耳机的选择非常多,音质、续航和佩戴的舒适度是我们选择…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...
