四边形不等式优化
四边形不等式优化
应用于类似以下dp转移方程。
f i = min 1 ≤ j ≤ i ( w i , j , f i ) f_{i}=\min_{1\le j\le i}(w_{i,j},f_{i}) fi=1≤j≤imin(wi,j,fi)
假设 w i , j w_{i,j} wi,j 可以在 O ( 1 ) O(1) O(1) 的时间内进行计算。
在正常情况下,此状态转移方程的时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
对于问题 i i i,我们需要考虑所有的有关决策 j j j,但是当其满足决策单调性时,就可以缩小决策空间,减少时间复杂度。
四边形不等式:
约定:
对于类似 a ≤ b ≤ c ≤ d a\le b\le c\le d a≤b≤c≤d 都成立,若二元函数 w i , j w_{i,j} wi,j 满足以下条件
w a , c + w b , d ≤ w a , d + w b , c w_{a,c}+w_{b,d}\le w_{a,d}+w_{b,c} wa,c+wb,d≤wa,d+wb,c
则称 w i , j w_{i,j} wi,j 满足四边形不等式。
特别的,若等号永远成立,则称 w i , j w_{i,j} wi,j 为四边形恒等式。
重点:因为四边形不等式是用来优化时间复杂度的,所以四边形不等式给出了一个决策单调性的充分不必要条件。
利用决策单调性,可以使用二分查找,使其查询时间复杂度降低为 O ( N log N ) O(N \log N) O(NlogN)。
区间包含单调性
若 w b , c ≤ w a , d w_{b,c}\le w_{a,d} wb,c≤wa,d,则称 w w w 满足区间包含单调性。
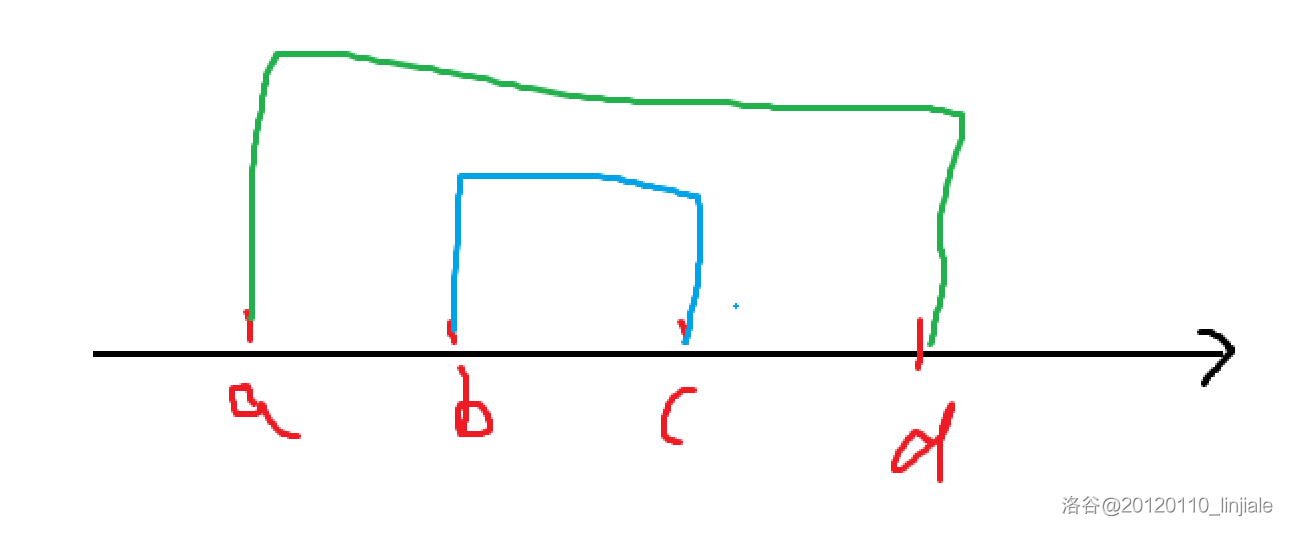
- 既包含,又满足决策单调性。
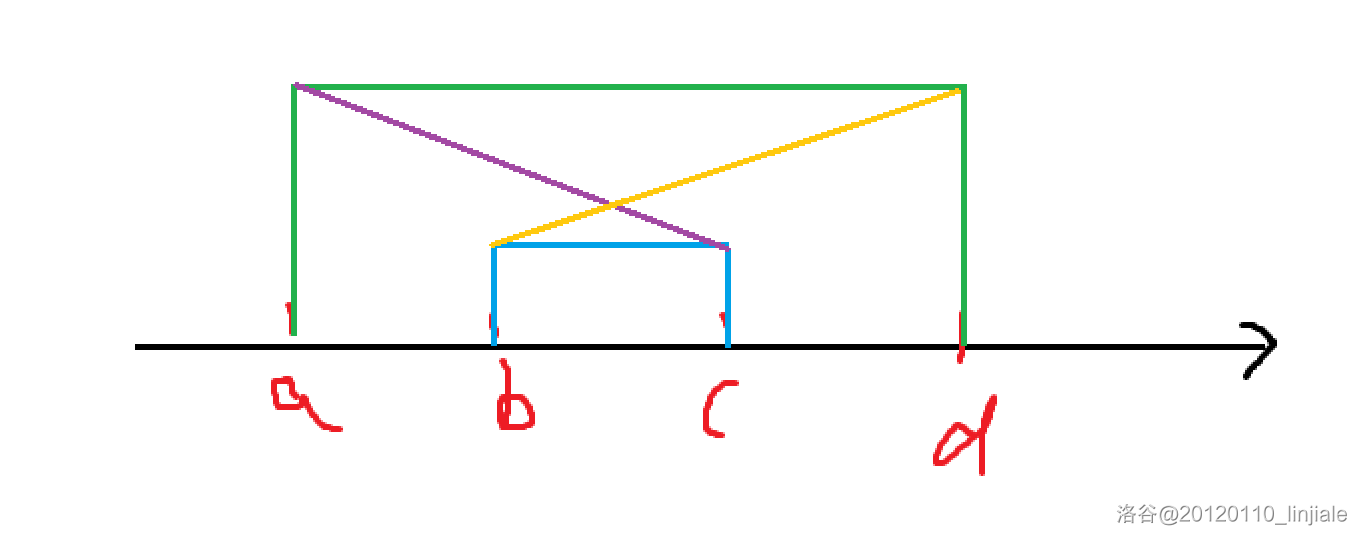
- 满足四边形不等式的形象化图片。
方程:
$$
w_{l,r+1}-w_{l,r}=a_{r+1}-a_{\lfloor\frac{l+r+1}{2}\rfloor}
\
w_{l+1,r+1}-w_{l+1,r}=a_{r+1}-a_{\lfloor\frac{l+r+2}{2}\rfloor}
\
$$
相关文章:

四边形不等式优化
四边形不等式优化 应用于类似以下dp转移方程。 f i min 1 ≤ j ≤ i ( w i , j , f i ) f_{i}\min_{1\le j\le i}(w_{i,j},f_{i}) fi1≤j≤imin(wi,j,fi) 假设 w i , j w_{i,j} wi,j 可以在 O ( 1 ) O(1) O(1) 的时间内进行计算。 在正常情况下,…...

这家民营银行起诉担保公司?暴露担保增信兜底隐患
来源 | 镭射财经(leishecaijing) 助贷领域中,各路资方依赖担保增信业务扩张数年,其风险积压也不容忽视。一旦助贷平台或担保公司兜不住底,资方就将陷入被动。 最近,一则民营银行起诉合作担保公司的消息引…...
vscode禅模式怎么退出
1、如何进入禅模式:查看--外观--禅模式 2、退出禅模式 按二次ESC,就可以退出。...
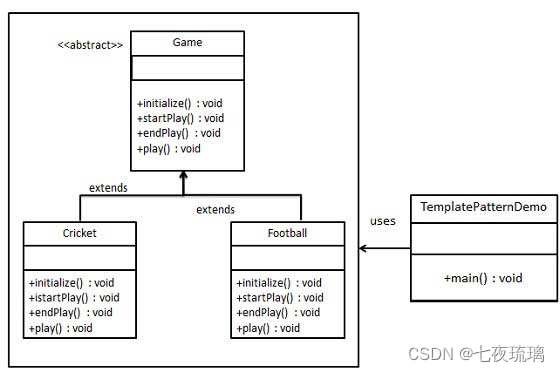
Java23种设计模式(四)
1、备忘录模式 备忘录模式(Memento Pattern)保存一个对象的某个状态,以便在适当的时候恢复对象,备忘录模式属于行为型模式。 备忘录模式允许在不破坏封装性的前提下,捕获和恢复对象的内部状态。 实现方式 创建备忘录…...

HTML静态网页成品作业(HTML+CSS)——故宫介绍网页(4个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有4个页面。 二、作品演示 三、代…...

Zookeeper:客户端命令行操作
文章目录 一、help二、ls path三、create四、get path五、set六、stat七、delete八、deleteall 一、help 显示所有操作命令。 二、ls path 使用ls命令来查看当前znode的子节点[可监听] w:监听子节点变化。s:附加次级信息。 三、create 普通创建&am…...

区块链技术介绍和用法
区块链技术是一种分布式账本技术,可以记录和存储一系列交易信息,并通过密码学算法保证信息的安全性和不可篡改性。区块链技术的核心概念是“区块”和“链”。 每个区块包含了一部分交易信息,以及一个指向上一个区块的哈希值。当新的交易发生…...

Upload-Labs-Linux1 使用 一句话木马
解题步骤: 1.新建一个php文件,编写内容: <?php eval($_REQUEST[123]) ?> 2.将编写好的php文件上传,但是发现被阻止,网站只能上传图片文件。 3.解决方法: 将php文件改为图片文件(例…...
从 Hadoop 迁移,无需淘汰和替换
我们仍然惊讶于有如此多的客户来找我们,希望从HDFS迁移到现代对象存储,如MinIO。我们现在以为每个人都已经完成了过渡,但每周,我们都会与一个决定进行过渡的主要、高技术性组织交谈。 很多时候,在这些讨论中ÿ…...
深度学习:从理论到应用的全面解析
引言 深度学习作为人工智能(AI)的核心技术之一,在过去的十年中取得了显著的进展,并在许多领域中展示了其强大的应用潜力。本文将从理论基础出发,探讨深度学习的最新进展及其在各领域的应用,旨在为读者提供全…...

【02】区块链技术应用
区块链在金融、能源、医疗、贸易、支付结算、证券等众多领域有着广泛的应用,但是金融依旧是区块链最大且最为重要的应用领域。 1. 区块链技术在金融领域的应用 1.2 概况 自2019年以来,国家互联网信息办公室已发布八批境内区块链信息服务案例清单&#…...

一篇文章搞懂残差网络算法
残差网络(Residual Network,简称ResNet)是一种深度学习架构,它在2015年由微软研究院的Kaiming He等四位作者提出。ResNet的提出是为了解决深度神经网络训练中的梯度消失和梯度爆炸问题,以及随着网络层数增加而出现的性能退化问题。本文将详细介绍残差网络算法的定义、产生…...
网络安全:Web 安全 面试题.(SQL注入)
网络安全:Web 安全 面试题.(SQL注入) 网络安全面试是指在招聘过程中,面试官会针对应聘者的网络安全相关知识和技能进行评估和考察。这种面试通常包括以下几个方面: (1)基础知识:包括网络基础知识、操作系…...
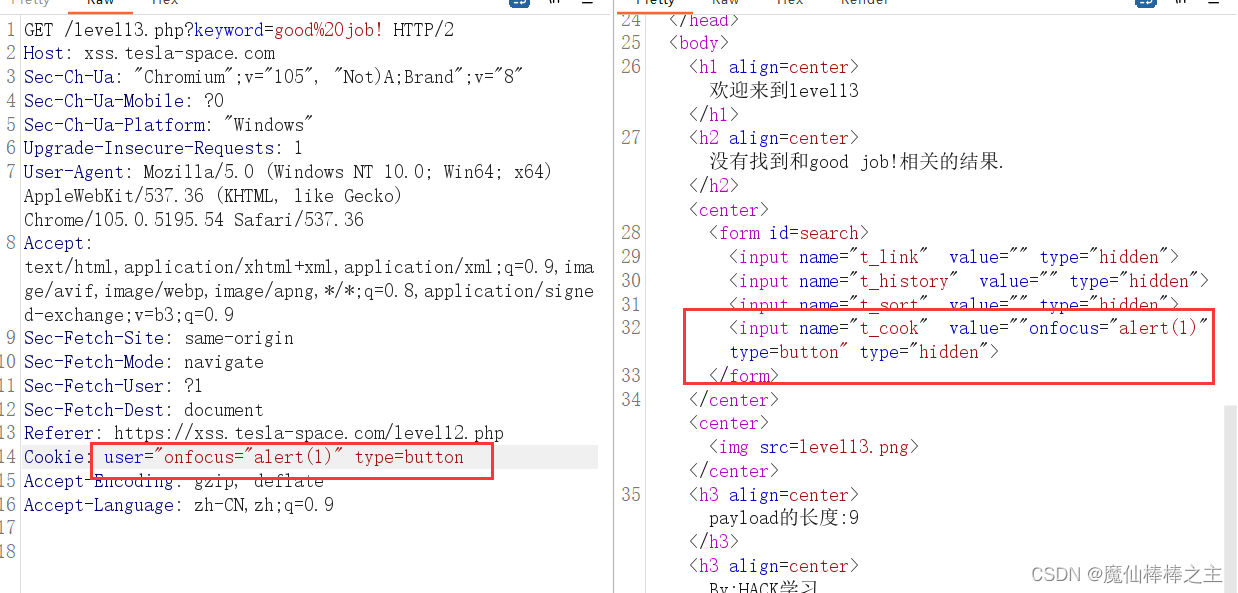
XSS学习(绕过)
学习平台:xss.tesla-space.com XSS学习(绕过) level1level2level3level4level5level6level7level8level9level10level11level12level13level14 level1 应该没有过滤 https://xss.tesla-space.com/level1.php?name<script>alert(1);&…...

深信服2024笔试
一 :服务器 小明是一名公司的IT运维工程师,负责管理公司的IT系统。公司总共有两个配置相同的服务器A和B,各运行了若干个服务。现在小明发现两台服务器上运行的服务占用的内存总和不相等(假设每个服务占用内存是-个恒定正整数),打…...

IOS Swift 从入门到精通:闭包 第一部分
文章目录 创建基本闭包在闭包中接受参数从闭包返回值闭包作为参数尾随闭包语法 创建基本闭包 Swift 允许我们像使用字符串和整数等其他类型一样使用函数。这意味着您可以创建一个函数并将其分配给一个变量,使用该变量调用该函数,甚至可以将该函数作为参…...

解两道四年级奥数题(等差数列)玩玩
1、1~200这200个连续自然数的全部数字之和是________。 2、2,4,6,……,2008这些偶数的所有各位数字之和是________。 这两道题算易错吧,这里求数字之和,比如124这个数的全部数字之和是1247。 …...

深入理解Python中的并发与异步的结合使用
在上一篇文章中,我们讨论了异步编程中的性能优化技巧,并简单介绍了trio和curio库。今天,我们将深入探讨如何将并发编程与异步编程结合使用,并详细讲解如何利用trio和curio库优化异步编程中的性能。 文章目录 并发与异步编程的区…...

如何将 ChatGPT 集成到你的应用中
在当今快速发展的技术环境中,将人工智能聊天解决方案集成到你的应用程序中可以显著提升用户体验和参与度。OpenAI 的 ChatGPT 以其对话能力和高级语言理解而闻名,对于希望在其应用程序中实现智能聊天功能的开发人员来说是一个绝佳的选择。那我们今天就来…...

在 Swift 中,UILabel添加点击事件的方法
在 Swift 中,可以使用 UITapGestureRecognizer 给 UILabel 添加点击事件。以下是一个详细的步骤和示例代码: 1. 创建 UILabel 并添加到视图 在 Storyboard 或代码中创建一个 UILabel 并将其添加到视图中。 2. 启用 UILabel 的用户交互 默认情况下&am…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
