【动态规划】多重背包问题,分组背包问题
Halo,这里是Ppeua。平时主要更新C语言,C++,数据结构算法......感兴趣就关注我吧!你定不会失望。
🌈个人主页:主页链接
🌈算法专栏:专栏链接
我会一直往里填充内容哒!
🌈LeetCode专栏:专栏链接
目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目,也会当天做完发出
🌈代码仓库:Gitee链接
🌈点击关注=收获更多优质内容🌈
目录
题目:多重背包问题
题解:
代码实现:
优化:
代码实现:
题目:分组背包问题
题解:
代码实现:
完结撒花:
题目:多重背包问题
题解:
与完全背包问题不同的是,每种东西都是有限件,前两种状态就不再过多赘述,有疑问的uu们可以去看看这篇文章完全背包,第三种状态我们直接枚举即可:当能拿下k个物品时,与不拿k件物品去最大值。
代码实现:
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1100;
int v[N],s[N],w[N],f[N][N];int main()
{int n=0,V=0;cin>>n>>V;for(int i=1;i<=n;i++){cin>>v[i]>>w[i]>>s[i];}for(int i=1;i<=n;i++){for(int j=1;j<=V;j++){for(int k=0;k*v[i]<=j&&k<=s[i];k++)f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+w[i]*k);}}cout<<f[n][V];
}
优化:
这种做法虽然简单易懂,但时间复杂度为n^3,很容易就TLE了,所以我们必须优化一下。
这里有利用了一下快速幂(背增)的思想,不知道的uu们听我细说:
任何一个正整数都可以由二进制来表示(废话,那么我们要取得价值是不是也可以由二进制表示呢?
例如 我们有 1 2 4价值得东西,那我们就可以由这三个东西凑出0~7之间任何一个数
(由3个物品的表示凑出了7个情况),效率就高了
假设我们要凑0~9的任何一个数呢,那么1 2 4就无法表示了,我们可以给这区间加上一个2,是不是就可以表示0~9之间的任何一个情况了呢。
换到这题来看,数量为s的物品可以拆分为log s 个东西,就可以枚举出s个物品的情况,对应的价值乘上倍数k即可满足上面所说情况,所以对应的问题就变成了01背包问题
代码实现:
#include<iostream>
#include<algorithm>
using namespace std;
const int N=110000000;
int v[N],s[N],w[N],f[N][N];int solution2()
{int n=0,V=0;cin>>n>>V;int cnt=0;int k=1;for(int i=1;i<=n;i++){int a=0,b=0,s=0;cin>>a>>b>>s;int k=1;while(k<=s){v[++cnt]=a*k;w[cnt]=b*k; s-=k;k*=2;}if(s>0){v[++cnt]=s*a;w[cnt]=s*b;}}n=cnt;for(int i=1;i<=n;i++){for(int j=V;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+w[i]);}cout<<f[V];
}题目:分组背包问题
题解:
这题与完全背包问题也十分的相似,就是将一件物品无限拿,变成了一组物品挑一个。
代码实现:
#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int v[N][N],w[N][N],s[N],f[N];
int main()
{int n=0,m=0;cin>>n>>m;for(int i=1;i<=n;i++){cin>>s[i];for(int j=0;j<s[i];j++){cin>>v[i][j];cin>>w[i][j];}}for(int i=1;i<=n;i++){for(int j=m;j>=0;j--){for(int k=0;k<s[i];k++){if(j>=v[i][k])f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);}}}cout<<f[m];
}完结撒花:
🌈本篇博客的内容【动态规划:多重背包问题,分组背包问题】已经结束。
🌈若对你有些许帮助,可以点赞、关注、评论支持下博主,你的支持将是我前进路上最大的动力。
🌈若以上内容有任何问题,欢迎在评论区指出。若对以上内容有任何不解,都可私信评论询问。
🌈诸君,山顶见!
相关文章:

【动态规划】多重背包问题,分组背包问题
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...

JAVA面向对象特征之——封装
4.封装 private关键字 是一个权限修饰符 可以修饰成员(成员变量和成员方法) 作用是保护成员不被别的类使用,被private修饰的成员只在本类中才能访问 针对private修饰的成员变量,如果需要被其他类使用,提供相应的操作 提供 “get变量名()…...

【数据结构】二叉树相关OJ题
文章目录一、单值二叉树二、检查两颗树是否相同三、判断一棵树是否为另一颗树的子树四、对称二叉树五、二叉树的前序遍历六、二叉树中序遍历七、二叉树的后序遍历八、二叉树的构建及遍历一、单值二叉树 单值二叉树 题目描述 如果二叉树每个节点都具有相同的值,那…...
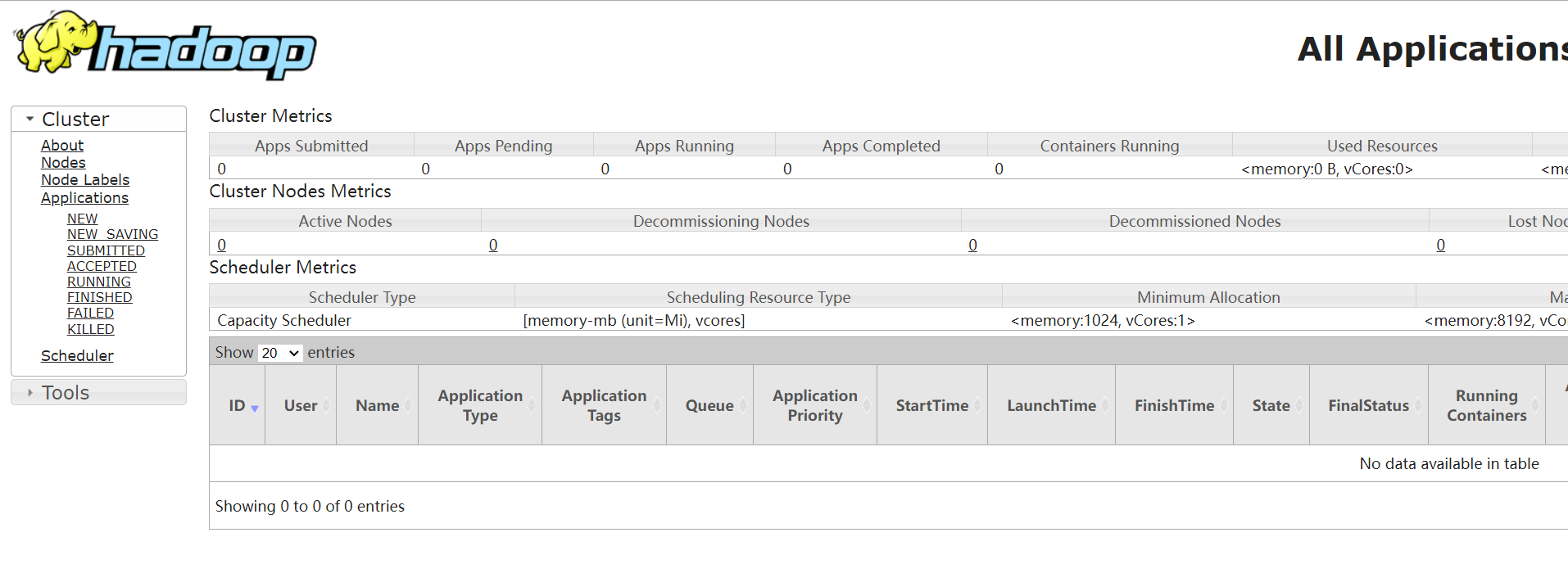
Windows安装Hadoop
当初搭建Hadoop、Hive、HBase、Flink等这些没有截图写文,今为分享特重装。下载Hadoop下载地址:https://mirrors.tuna.tsinghua.edu.cn/apache/hadoop/以管理员身份运行cmd切换到所在目录执行start winrar x -y hadoop-3.3.4.tar.gz,解压。配置…...
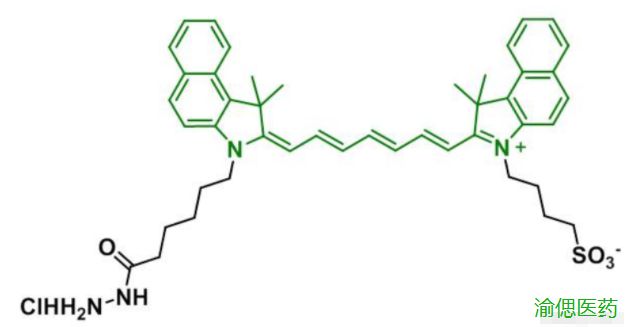
ICG-Hydrazide,吲哚菁绿-酰肼,ICG-HZ结构式,溶于二氯甲烷等部分有机溶剂,
ICG-Hydrazide,吲哚菁绿-酰肼 中文名称:吲哚菁绿-酰肼 英文名称:ICG-Hydrazide 英文别名:ICG-HZ 性状:粉末或固体 溶剂:溶于二氯甲烷等部分有机溶剂 稳定性:-20℃密封保存、置阴凉干燥处、防潮 分子…...
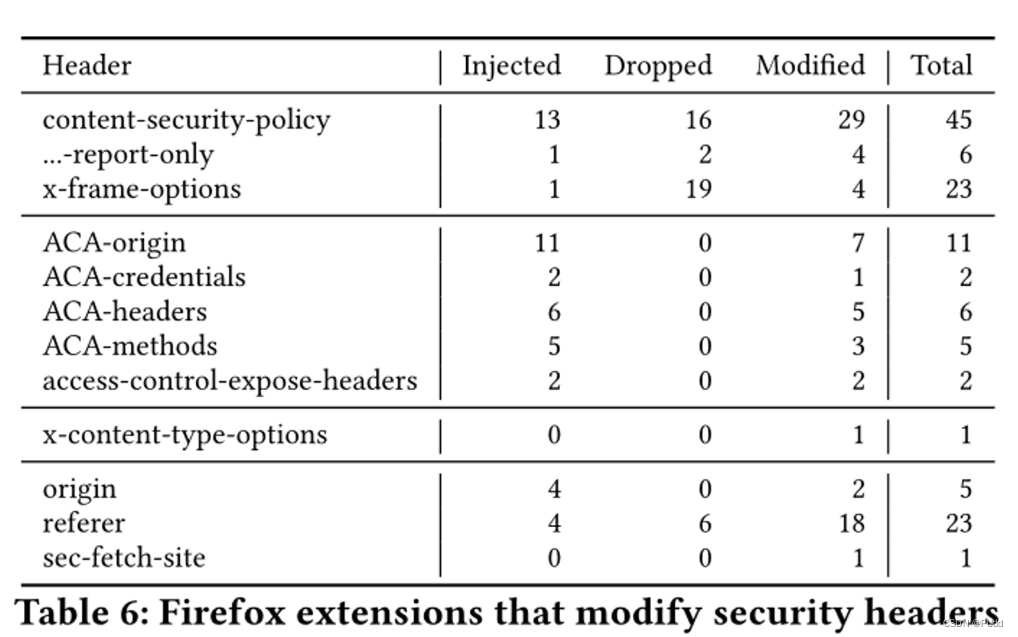
【论文阅读】浏览器扩展危害-Helping or Hindering? How Browser Extensions Undermine Security
本文来源于ACM CCS 2022; https://dl.acm.org/doi/10.1145/3548606.3560685 摘要 “浏览器扩展”是轻量级的浏览器附加组件,使用各个浏览器特定的功能丰富的JavaScript api,为用户提供了额外的Web客户端功能,如改进网站外观和与…...
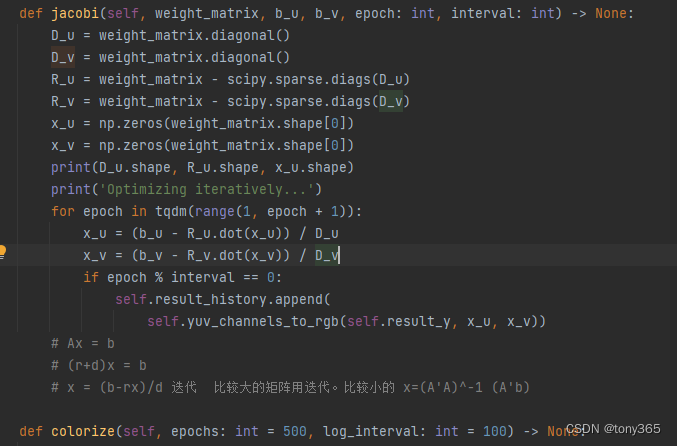
线性和非线性最小二乘问题的常见解法总结
线性和非线性最小二乘问题的各种解法 先看这篇博客,非常好:线性和非线性最小二乘问题的各种解法 1. 线性最小二乘问题有最优解 但是面对大型稀疏矩阵的时候使用迭代法效率更好。 迭代法 有Jacobi迭代法、 Seidel迭代法及Sor法 【数值分析】Jacobi、Se…...

数据库知识点
数据库是指按照一定规则存储、组织和管理数据的系统。在现代化的信息化社会中,数据库已经成为了各种应用系统中不可或缺的一部分。因此,对于数据库的知识掌握不仅是计算机专业人员必备的技能,也是各个行业从业者必须具备的基本素质之一。 数…...

Maven打包构建Docker镜像并推送到仓库
Maven打包构建Docker镜像并推送到仓库 文章目录Maven打包构建Docker镜像并推送到仓库一,服务器Docker配置二,本地项目maven配置2.1 pom.xml2.2 dockerfile2.3 验证2.4 统一dockerfile对于开发完成的服务要发布至服务器Docker时,我刚学习了解D…...

TypeScript 基础学习之泛型和 extends 关键字
越来越多的团队开始使用 TS 写工程项目, TS 的优缺点也不在此赘述,相信大家都听的很多了。平时对 TS 说了解,仔细思考了解的也不深,借机重新看了 TS 文档,边学习边分享,提升对 TS 的认知的同时,…...
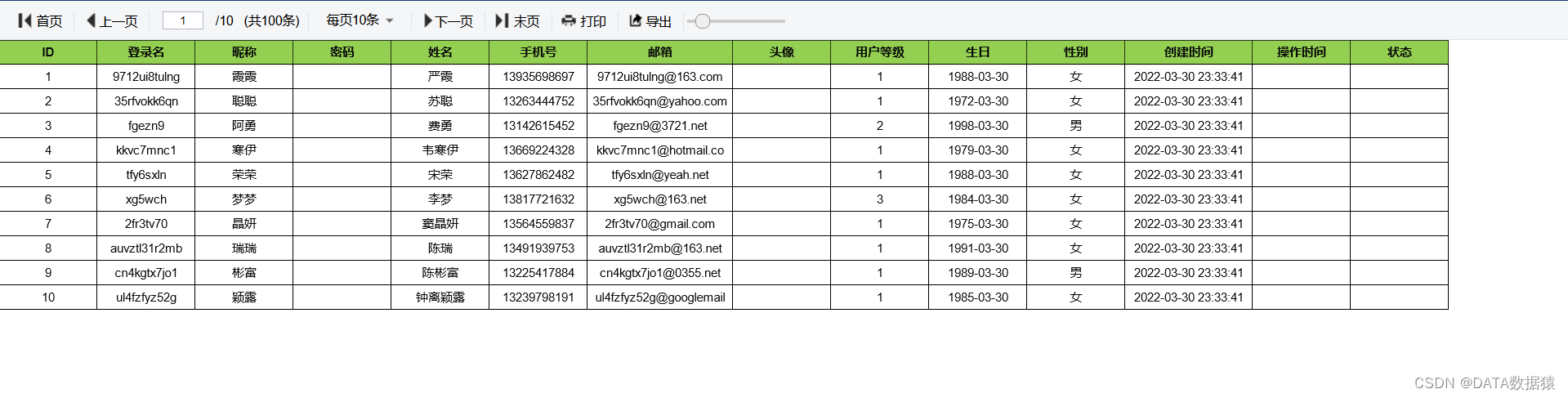
《数据分析-JiMuReport04》JiMuReport报表设计入门介绍-页面优化
报表设计 2 页面优化 如上图所示的报表,仅仅是展示数据,不过这样看起来似乎太草率了,所以再优化一下吧 保存报表后,在积木报表中就可以看到对应的报表文件 此时我们如果还需要编辑报表,就点击这个报表即可 2.1 居中…...
带头双向循环链表及链表总结
1、链表种类大全 1、链表严格来说可能用2*2*28种结构,从是否带头,是否循环,是否双向三个角度区分。 2、无头单向循环链表一般不会在实际运用中直接存储数据,而会作为某些更复杂结构的一个子结构,毕竟它只在头插、头删…...
MySQL是如何基于各种规则去优化执行计划的?(中))
(八十)MySQL是如何基于各种规则去优化执行计划的?(中)
今天我们来讲一下子查询是如何执行的,以及他的执行计划是如何优化的。比如说类似于下面的SQL语句: select * from t1 where x1 (select x1 from t2 where idxxx) 这就是一个典型的子查询 也就是说上面的SQL语句在执行的时候,其实会被拆分为…...

第一章:命题与命题公式
1.命题与命题联结词 1.命题与命题的表示 1. 命题 由一个或几个已知的前提,推导出来一个未知的结论的思维过程称为推理,推理的基本要素就是表达这些前提的一些陈述句,可以将这些陈述句理解为命题。 (1)地球是行星 (2)8不是素数 (3)1 + 2 = 22. 命题真值 一个陈述句不…...
,操作符重载)
c/c++开发,无可避免的操作符operator(篇一),操作符重载
一、操作符号重载 虽然c/c内置了大量各类操作符,开发者可以很方便将其应用数学运算、成员访问、类型转换、内存分配等执行语句中,但很多时候,也需要根据项目应用需要,通过操作符重载,能够针对类类型的操作数定义不同的…...

【7.MySQL行格式存储】
1.MySQL数据存放文件 我们每创建一个 database(数据库) 都会在 /var/lib/mysql/ 目录里面创建一个以 database 为名的目录,创建一个student表 [rootxiaodainiao ~]#ls /var/lib/mysql/my_test db.opt student.frm student.ibddb.opt:用…...

【Linux】线程实例 | 简单线程池
今天来写一个简单版本的线程池 1.啥是线程池 池塘,顾名思义,线程池就是一个有很多线程的容器。 我们只需要把任务交到这个线程的池子里面,其就能帮我们多线程执行任务,计算出结果。 与阻塞队列不同的是,线程池中内有…...

ATAC-seq 数据分析实战
文章目录一、 ATAC-seq原理和基础知识1. ATAC-seq原理2. Tn5转座子1. 转座概念2. 参与分子1. 转座子(1) 简化的转座子结构(2) Tn5转座子的结构2. 转座酶3. 转座过程二、数据比对和过滤一、 ATAC-seq原理和基础知识 1. ATAC-seq原…...
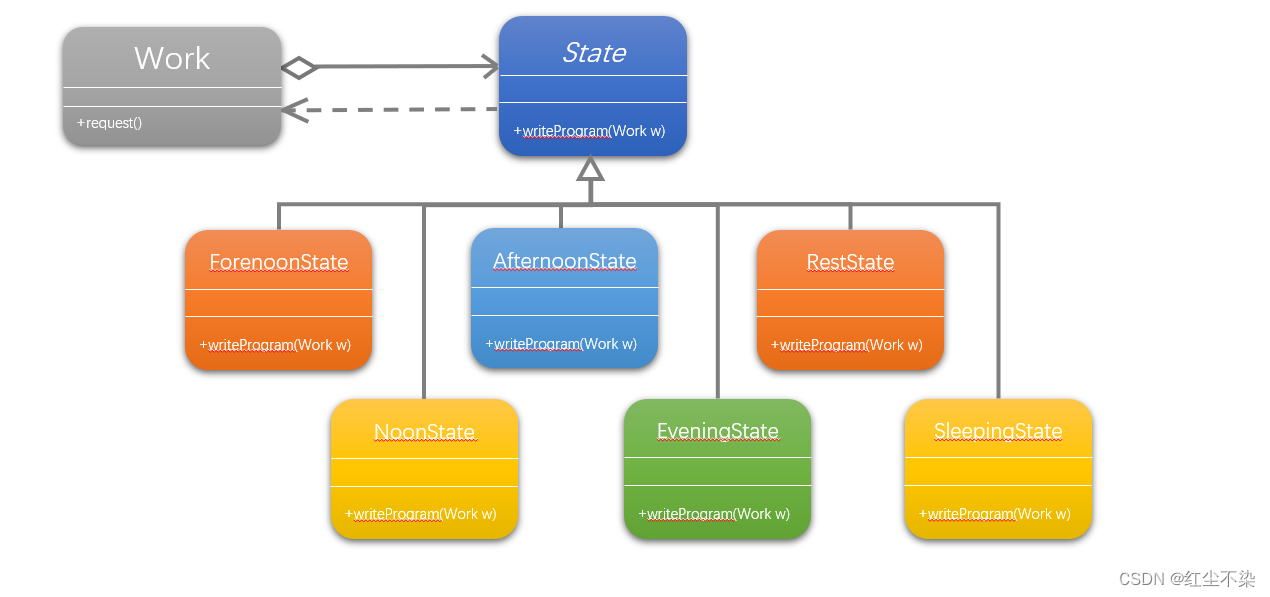
设计模式-第13章(状态模式)
状态模式状态模式状态模式的好处和用处工作状态状态模式 状态模式(State),当一个对象的内在状态改变时允许改变其行为,这个对象看起来像是改变了其类。 状态模式主要解决的是当控制一个对象状态转换的条件表达式过于复杂时的情况…...
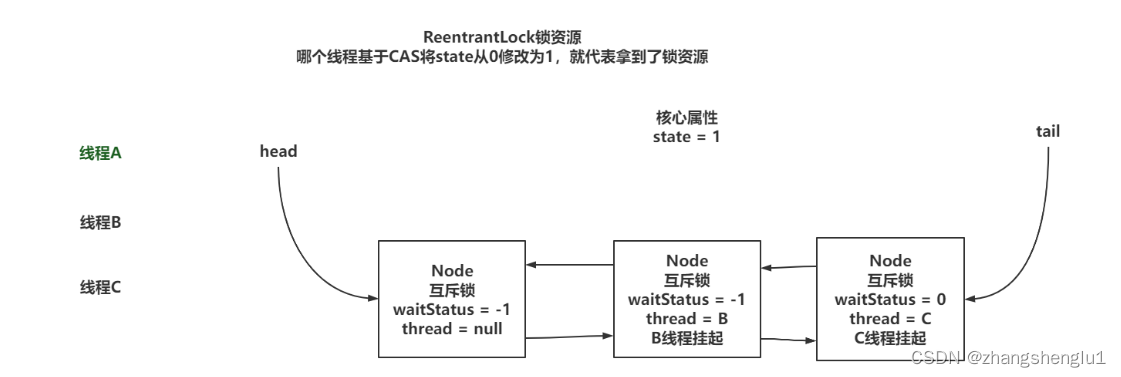
ReentrantLock源码分析(一)加锁流程分析
一、ReetrantLock的使用示例 static ReentrantLock lock new ReentrantLock(); public static void main(String[] args) throws InterruptedException { new Thread(ClassLayOutTest::reentrantLockDemo, "threadA").start(); Thread.sleep(1000);…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...
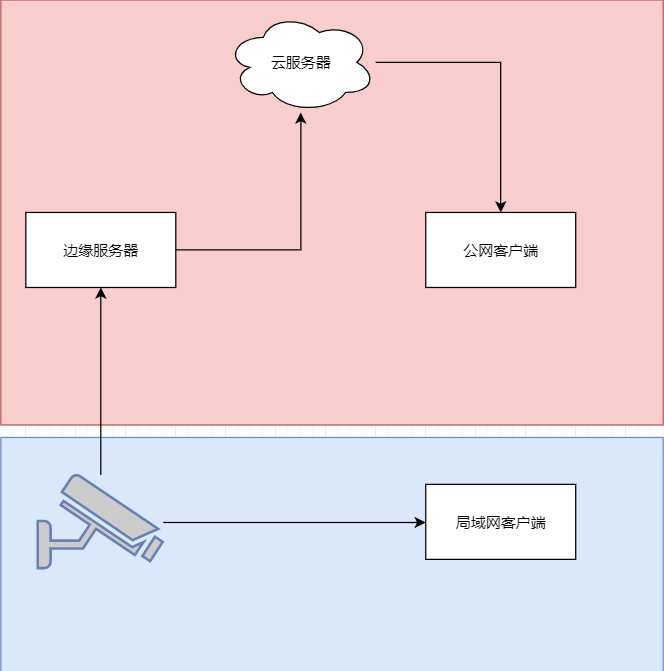
java 局域网 rtsp 取流 WebSocket 推送到前端显示 低延迟
众所周知 摄像头取流推流显示前端延迟大 传统方法是服务器取摄像头的rtsp流 然后客户端连服务器 中转多了,延迟一定不小。 假设相机没有专网 公网 1相机自带推流 直接推送到云服务器 然后客户端拉去 2相机只有rtsp ,边缘服务器拉流推送到云服务器 …...

今日行情明日机会——20250609
上证指数放量上涨,接近3400点,个股涨多跌少。 深证放量上涨,但有个小上影线,相对上证走势更弱。 2025年6月9日涨停股主要行业方向分析(基于最新图片数据) 1. 医药(11家涨停) 代表标…...

AI书签管理工具开发全记录(十八):书签导入导出
文章目录 AI书签管理工具开发全记录(十八):书签导入导出1.前言 📝2.书签结构分析 📖3.书签示例 📑4.书签文件结构定义描述 🔣4.1. 整体文档结构4.2. 核心元素类型4.3. 层级关系4.…...