当前位置： 首页 > news >正文

网络协议安全：TCP/IP协议栈的安全问题和解决方案

news 2026/2/9 14:40:14

「作者简介」：北京冬奥会网络安全中国代表队，CSDN Top100，就职奇安信多年，以实战工作为基础对安全知识体系进行总结与归纳，著作适用于快速入门的 《网络安全自学教程》，内容涵盖Web安全、系统安全等12个知识域的一百多个知识点，持续更新。

这一章节我们需要知道TCP/IP每层存在哪些安全问题，每一层的解决方式是什么，重点是网络层的IPsec和传输层的SSL。

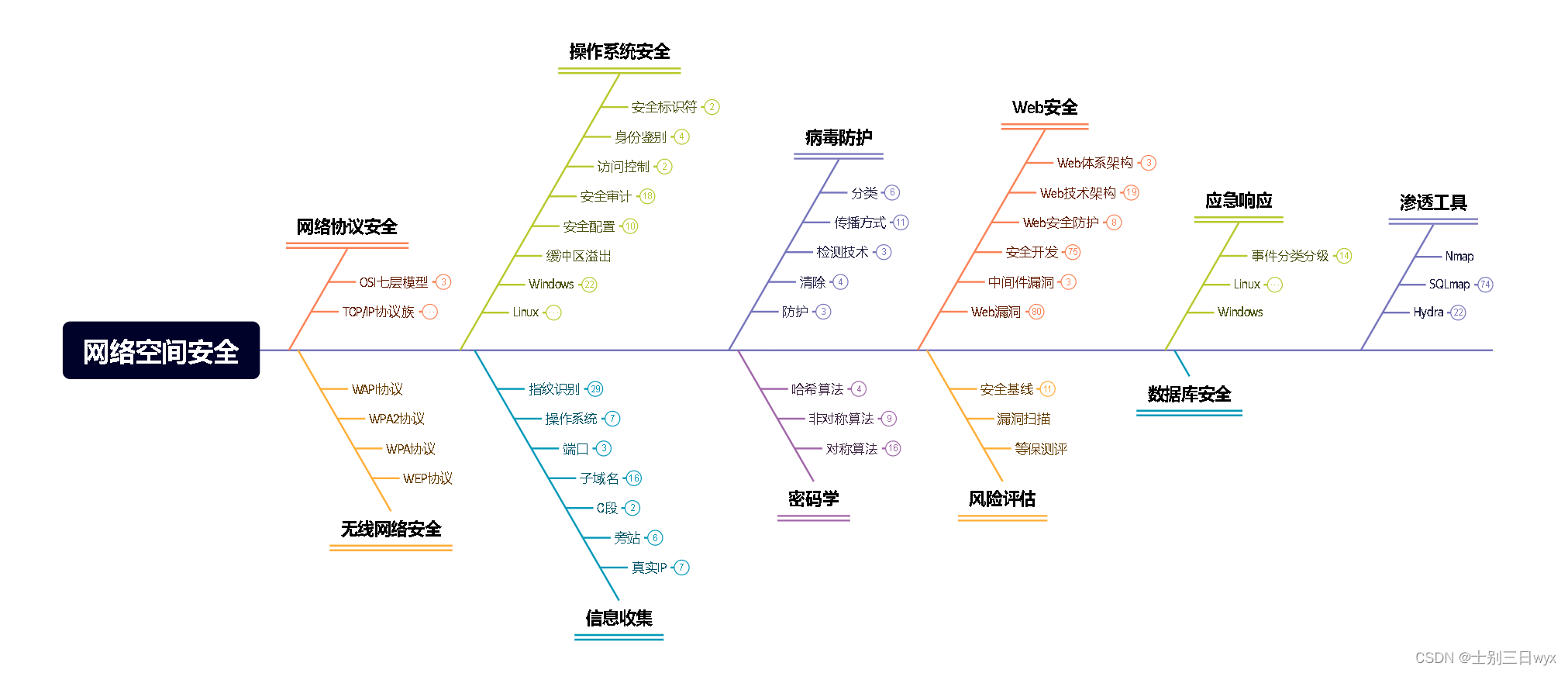
在这里插入图片描述

TCP/IP协议栈

  • 1、网络接口层的安全问题
    • 2.1、ARP欺骗
    • 2.2、嗅探
    • 2.3、拒绝服务
      • 2.3.1、MAC flooding
      • 2.3.1、ARP flooding
  • 2、网络层的安全问题
    • 2.1、IP欺骗
    • 2.2、拒绝服务
  • 3、传输层的安全问题
    • 3.1、TCP会话劫持
    • 3.2、拒绝服务
      • 3.2.1、SYN Flood
      • 3.2.2、UDP Flood
  • 4、应用层的安全问题

TCP/IP协议簇是以TCP协议和IP协议为核心、由多种协议组成的「协议栈」，是一组协议的集合。

因为OSI是理想化的七层模型，所以TCP/IP协议簇从「实用性」的角度出发，将OSI七层参考模型简化为四层模型。从上往下依次是应用层、传输层、网络互联层、网络接口层。

在这里插入图片描述

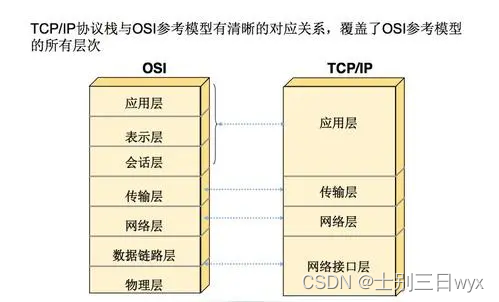
TCP/IP协议栈起初是为了网络互联互通设计的，主要应用在大学、研究所等区域，那种场景下，网络是可信的。随着互联网的发展，个人PC加入到网络以后，开始出现嗅探、拒绝服务等攻击。解决这些安全隐患，

相关文章：

网络协议安全：TCP/IP协议栈的安全问题和解决方案

「作者简介」：北京冬奥会网络安全中国代表队，CSDN Top100，就职奇安信多年，以实战工作为基础对安全知识体系进行总结与归纳，著作适用于快速入门的 《网络安全自学教程》，内容涵盖Web安全、系统安全等12个知识域的一百多个知识点，持续更新。 这一章节我们需要知道TCP/IP每…...

编程日记 2024/6/25 6:42:00

VERYCLOUD睿鸿股份亮相亚马逊云科技中国峰会2024

5月30日，为期两天的亚马逊云科技中国峰会在上海世博中心圆满落幕。 多位大咖现场分享，生成式AI时代的数据战略，企业级AI应用，最新技术、产品重磅发布，创新行业解决方案 …… 作为亚马逊云科技的生态合作伙伴&#x…...

编程日记 2024/6/25 6:40:58

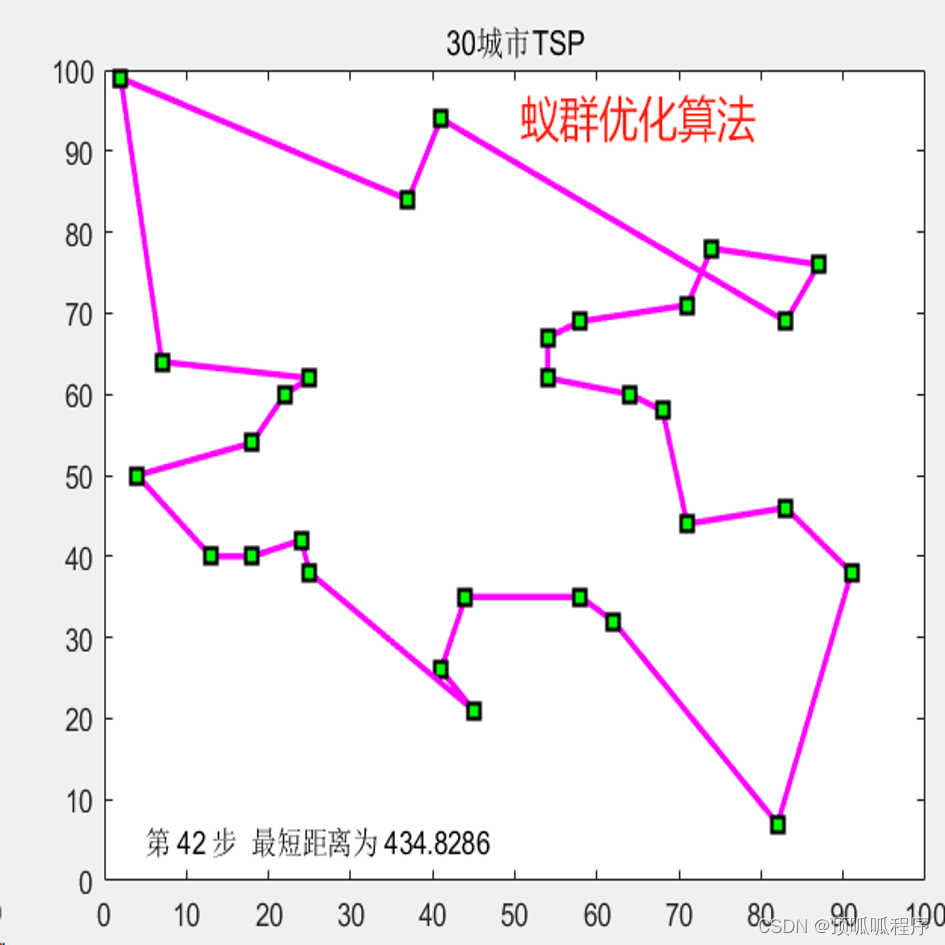
2-15 基于matlab的蚁群，模拟退火，遗传，神经网络，禁忌搜索等智能优化算法对TSP问题

基于matlab的蚁群，模拟退火，遗传，神经网络，禁忌搜索等智能优化算法对TSP问题。五种优化算法对多个城市路径进行规划，通过优化速度、距离可比较五种方法的优劣。程序已调通，可直接运行。 2-15 蚁群优化算法 …...

编程日记 2024/6/25 6:34:52

kylinos 国产操作系统离线安装firefox 麒麟操作系统安装新版本firefox

1. 火狐地址： 下载 Firefox 浏览器，这里有简体中文及其他 90 多种语言版本供您选择 2. 选择： 3. 下载完之后，上传到离线机器 4. 解压缩： tar -xvjf firefox-127.0.1.tar.bz2 5. 去点击解压后的文件夹，找…...

编程日记 2024/6/25 6:32:50

Python 类对象

Python 类对象 经典迭代器 可迭代对象的定义： 使用内置的iter可以获取迭代器的对象。如果对象实现了能返回迭代器的__iter__方法，那么对象就是可迭代的。序列都可以迭代。实现了__getitem__方法，而且接受从0开始的索引，这种对象也…...

编程日记 2024/6/25 6:31:48

pytest unittest temp path单元测试创建临时文件

参考了这个：Test Files Creating a Temporal Directory in Python Unittests | Simple IT 🤘 Rocks 并使用pathlib做了优化： import tempfile import unittest from pathlib import Pathclass TestExample(unittest.TestCase):def test_exa…...

编程日记 2024/6/25 6:30:47

在线样机生成器,制作精美的电脑手机壁纸图片展示

在线样机生成器，可以制作精美的电脑手机壁纸图片展示。在线样机生成器支持不同的模型如浏览器、手机、笔记本电脑、手表等结合使用，帮助用户快速生成样机展示图片。下面小编就来和大家分享一款免费的在线样机生成器-壁纸样机生成器。 壁纸样机生成器是一…...

编程日记 2024/6/25 6:29:46

FreeRTOS实时操作系统

1.认识实施操作系统 1.1 裸机和实时操作系统 裸机： 早期嵌入式开发没有嵌入式操作系统的概念，直接操作裸机，在裸机上写程序，比如用51单片机基本就没有操作系统的概念。 通常把程序设计为前后台系统，主要分为两部分&a…...

编程日记 2024/6/25 6:26:43

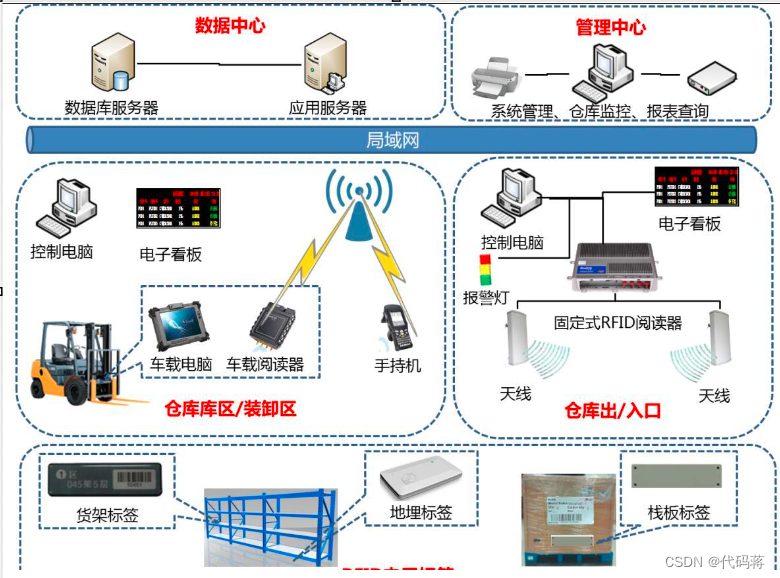
C/S、B/S架构（详解）

一、CS、BS架构定义 CS架构（Client-Server Architecture）是一种分布式计算模型，其中客户端和服务器之间通过网络进行通信。在这种架构中，客户端负责向服务器发送请求，并接收服务器返回的响应。服务器则负责处理客户端的…...

编程日记 2024/6/25 6:25:41

代码随想录算法训练营第六十五天|KM99. 岛屿数量——深搜、KM99. 岛屿数量——广搜、KM100. 岛屿的最大面积

代码随想录算法训练营第六十五天 KM99. 岛屿数量——深搜 题目链接：KM99. 岛屿数量 使用递归深度搜索，将每次遇到的岛屿上下左右记录为已经到过，如果遇到没到过的说明它上下左右不是之间遍历过的岛屿，结果计数1。最后统计计数即…...

编程日记 2024/6/25 6:23:40

Lua 面向对象编程

Lua 面向对象编程 Lua 是一种轻量级的编程语言，通常用于嵌入应用程序中，提供灵活的扩展和定制功能。尽管 Lua 本身是一种过程式语言，但它提供了强大的元机制，允许开发者实现面向对象的编程范式。本文将探讨 Lua 中的面向对象编程（OOP）概念、实现方式以及最佳实践。 面向…...

编程日记 2024/6/25 6:21:38

AI赋能前端：你的Chrome 控制台需要AI(爱)

像会永生那样去学习，像明天就要死亡那样去生活。——圣雄甘地 大家好，我是柒八九。一个专注于前端开发技术/Rust及AI应用知识分享的Coder 此篇文章所涉及到的技术有 AI(Gemini)ChromeDevTool🪜魔法接码平台因为，行文字数所限，有些概念可能会一带而过亦或者提供对应的学习…...

编程日记 2024/6/25 6:20:36

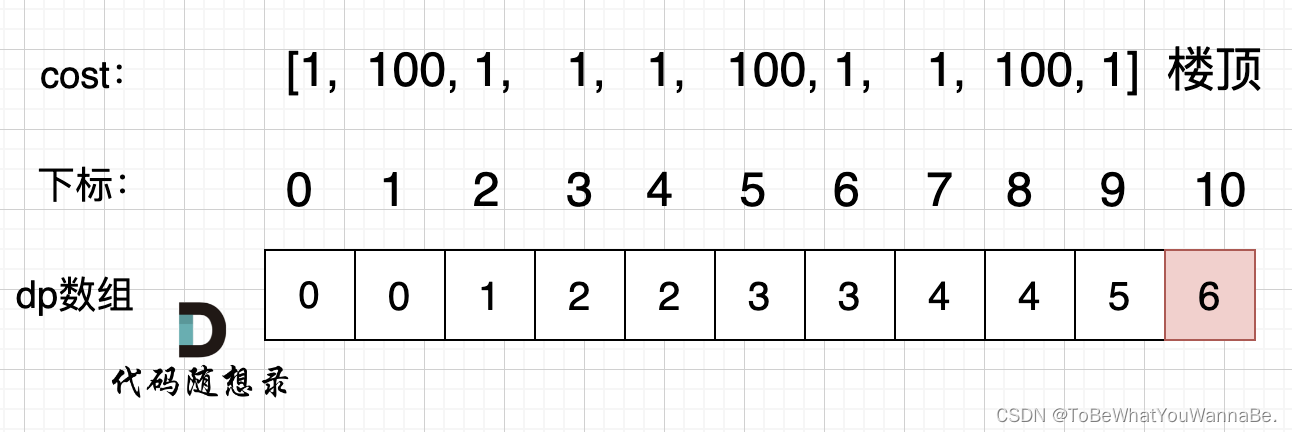
代码随想录-Day38

509. 斐波那契数 斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是： F(0) 0，F(1) 1 F(n) F(n - 1) F(n - 2)，其中 …...

编程日记 2024/6/25 6:18:35

CSS阴影优化气泡框样式

<body> <div class"pop">气泡框</div> </body>body{display: flex;justify-content: center;align-items: center;height: 100% } .pop{display: flex;justify-content: center;align-items: center;background: #409eff;width: 150px;heigh…...

编程日记 2024/6/25 6:17:32

强化安全新篇章：韶关石油化工可燃气体报警器年检解析

韶关&#xff0c;这座位于广东省北部的城市&#xff0c;近年来在石油化工行业取得了显著的发展。 随着一批批大型石化企业的进驻和投产&#xff0c;韶关不仅成为了区域性的石化产业基地&#xff0c;也为地方经济带来了强劲的增长动力。 然而&#xff0c;随着石化产业的快速发…...

编程日记 2024/6/25 6:16:31

Centos7 Docker部署PgSQL

拉取镜像 docker pull postgres:14.7运行容器 docker run --restartalways --nethost --shm-size"2g" --name pgsql -v /home/postgresql/data/pgdata:/var/lib/postgresql/data -v /etc/localtime:/etc/localtime -e POSTGRES_PASSWORDtest2023 -d postgres:14…...

编程日记 2024/6/25 6:15:30

LeetCode：经典题之21、24 题解及延伸

系列目录 88.合并两个有序数组 52.螺旋数组 567.字符串的排列 643.子数组最大平均数 150.逆波兰表达式 61.旋转链表 160.相交链表 83.删除排序链表中的重复元素 389.找不同 1491.去掉最低工资和最高工资后的工资平均值 896.单调序列 206.反转链表 92.反转链表II 141.环形链表 …...

编程日记 2024/6/25 6:14:29

【C++11】initializer_list详解！

一、什么是initializer_list? nitializer_list 是一种C11新的类型特性&#xff0c;它允许我们以统一的方式初始化对象。它是一个代表数组的轻量级包装器&#xff0c;通常用于构造函数和函数参数中&#xff0c;以允许传递一个初始化元素列表。 initializer_list也是一种模板类…...

编程日记 2024/6/25 6:13:27

如何在Java中处理UnsupportedOperationException异常？

如何在Java中处理UnsupportedOperationException异常&#xff1f; 大家好&#xff0c;我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编&#xff0c;也是冬天不穿秋裤&#xff0c;天冷也要风度的程序猿&#xff01; 在Java编程中&#xff0c;我们经常会遇到各…...

编程日记 2024/6/25 6:11:25

WPS没保存关闭了怎么恢复数据？4个方法（更新版）

想象一下&#xff0c;你正在用WPS奋笔疾书&#xff0c;灵感如泉水般涌出&#xff0c;突然间&#xff0c;电脑却跟你开了个玩笑——啪地一下&#xff0c;文档未保存就关闭了&#xff01;是不是感觉像是被泼了一盆冷水&#xff0c;所有的热情瞬间熄灭&#xff1f;别急&#xff0c…...

编程日记 2024/6/25 6:09:23

生成xcframework

打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式&#xff0c;可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

编程新知 2025/10/5 2:30:38

vscode里如何用git

打开vs终端执行如下&#xff1a; 1 初始化 Git 仓库&#xff08;如果尚未初始化&#xff09; git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

编程新知 2025/8/24 20:45:38

云计算——弹性云计算器（ECS）

弹性云服务器&#xff1a;ECS 概述 云计算重构了ICT系统&#xff0c;云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台&#xff0c;包含如下主要概念。 ECS&#xff08;Elastic Cloud Server&#xff09;&#xff1a;即弹性云服务器&#xff0c;是云计算…...

编程新知 2025/8/16 21:50:27

1688商品列表API与其他数据源的对接思路

将1688商品列表API与其他数据源对接时&#xff0c;需结合业务场景设计数据流转链路&#xff0c;重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点&#xff1a; 一、核心对接场景与目标 商品数据同步 场景&#xff1a;将1688商品信息…...

编程新知 2025/11/30 16:55:32

HTML 列表、表格、表单

1 列表标签 作用&#xff1a;布局内容排列整齐的区域 列表分类&#xff1a;无序列表、有序列表、定义列表。 例如&#xff1a; 1.1 无序列表 标签&#xff1a;ul 嵌套 li&#xff0c;ul是无序列表&#xff0c;li是列表条目。 注意事项&#xff1a; ul 标签里面只能包裹 li…...

编程新知 2026/1/24 22:33:33

江苏艾立泰跨国资源接力：废料变黄金的绿色供应链革命

在华东塑料包装行业面临限塑令深度调整的背景下&#xff0c;江苏艾立泰以一场跨国资源接力的创新实践&#xff0c;重新定义了绿色供应链的边界。 跨国回收网络&#xff1a;废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点&#xff0c;将海外废弃包装箱通过标准…...

编程新知 2026/1/31 13:42:15

WEB3全栈开发——面试专业技能点P2智能合约开发（Solidity）

一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解&#xff0c;适合用作学习或写简历项目背景说明。 &#x1f9e0; 一、概念简介&#xff1a;Solidity 合约开发 Solidity 是一种专门为 以太坊&#xff08;Ethereum&#xff09;平台编写智能合约的高级编…...

编程新知 2026/1/27 9:33:09

ardupilot 开发环境eclipse 中import 缺少C++

目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++，无法导入ardupilot代码，会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

编程新知 2026/1/31 5:06:34

06 Deep learning神经网络编程基础 激活函数 --吴恩达

深度学习激活函数详解 一、核心作用 引入非线性：使神经网络可学习复杂模式控制输出范围：如Sigmoid将输出限制在(0,1)梯度传递：影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

编程新知 2025/11/17 21:48:26

Caliper 配置文件解析：config.yaml

Caliper 是一个区块链性能基准测试工具，用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构，并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件，主要包含以下几个部…...

编程新知 2025/8/13 13:40:18