算法 Hw9
Hw 9
- 1 Scheduling with profits and deadlines
- 1
- 2
- 3
- 4
- 5
- 2 Parallel machine
- 1
- 2
- 3
- 4
1 Scheduling with profits and deadlines
1
决策问题表述:
给定一个利润值 P P P,是否存在一个任务调度方案使得完成所有任务的总利润至少为 P P P
2
在 NP 类中:
给定一个任务调度方案,可以在多项式时间内验证该方案的总利润是否至少为 P P P。验证过程包括检查每个任务是否在截止日期前完成,并计算总利润。因此,该问题在 NP 类中。
对于 NP 完全性:
- 给定一个 0/1 背包问题实例,其中有 n n n 个物品,每个物品有一个重量 w i w_i wi 和价值 v i v_i vi,以及一个总重量限制 W W W。
- 对应于调度问题中的每个任务 a j a_j aj,设置其处理时间 t j = w i t_j = w_i tj=wi,利润 p j = v i p_j = v_i pj=vi,并设置截止日期 d j = W d_j = W dj=W,保证任务必须在总时间 W W W 内完成。
- 利润值 P P P 设为背包问题中的价值总和的要求。
通过归约,若能在调度问题中找到一个利润至少为 P P P 的方案,则在 0/1 背包问题中可以找到一个总价值至少为 P P P 且总重量不超过 W W W 的物品选择方案。因此,调度问题的决策版本是 NP 完全的。
3
-
状态定义:设 d p [ t ] [ k ] dp[t][k] dp[t][k] 表示在总时间 t t t 内,选择前 k k k 个任务能获得的最大利润。
-
状态转移方程:
对于每个任务 a j a_j aj,有两种选择:- 不选择任务 a j a_j aj: d p [ t ] [ k ] = d p [ t ] [ k − 1 ] dp[t][k] = dp[t][k-1] dp[t][k]=dp[t][k−1]
- 选择任务 a j a_j aj(前提是 t ≥ t j t \geq t_j t≥tj 且 t ≤ d j t \leq d_j t≤dj): d p [ t ] [ k ] = max ( d p [ t ] [ k − 1 ] , d p [ t − t j ] [ k − 1 ] + p j ) dp[t][k] = \max(dp[t][k-1], dp[t-t_j][k-1] + p_j) dp[t][k]=max(dp[t][k−1],dp[t−tj][k−1]+pj)
-
初始状态:
- d p [ 0 ] [ 0 ] = 0 dp[0][0] = 0 dp[0][0]=0,表示没有时间且没有任务时的利润为 0。
-
算法步骤:
- 初始化 d p dp dp 数组为 0。
- 遍历所有任务,根据上述状态转移方程更新 d p dp dp 数组。
- 最终检查 d p [ T ] [ n ] dp[T][n] dp[T][n] 是否大于等于 P P P,其中 T T T 是计算机的总时间。
4
-
状态定义:设 d p [ t ] dp[t] dp[t] 表示在总时间 t t t 内能获得的最大利润。
-
状态转移方程:
对于每个任务 a j a_j aj,有两种选择:- 不选择任务 a j a_j aj: d p [ t ] = d p [ t ] dp[t] = dp[t] dp[t]=dp[t]
- 选择任务 a j a_j aj(前提是 t ≥ t j t \geq t_j t≥tj 且 t ≤ d j t \leq d_j t≤dj): d p [ t ] = max ( d p [ t ] , d p [ t − t j ] + p j ) dp[t] = \max(dp[t], dp[t-t_j] + p_j) dp[t]=max(dp[t],dp[t−tj]+pj)
-
初始状态:
- d p [ 0 ] = 0 dp[0] = 0 dp[0]=0,表示没有时间时的利润为 0。
-
算法步骤:
- 初始化 d p dp dp 数组为 0。
- 遍历所有任务,根据上述状态转移方程更新 d p dp dp 数组。
- 最终 d p [ T ] dp[T] dp[T] 即为最大利润,其中 T T T 是计算机的总时间。
5
由于上述动态规划算法是一个精确算法(在多项式时间内找到最优解),因此它的近似比为 1,即它能够找到最优解。
2 Parallel machine
1
考虑所有工作中处理时间最长的工作 J k J_k Jk,其处理时间为 p k = max { p j : 1 ≤ j ≤ n } p_k = \max\{p_j : 1 \leq j \leq n\} pk=max{pj:1≤j≤n}。
由于该工作必须在某台机器上连续运行 p k p_k pk 时间单位,且在此期间不能有其他工作在同一台机器上运行,因此该工作的完工时间至少为 p k p_k pk。
因此,最优完工时间 C max ∗ C^*_{\text{max}} Cmax∗ 必须至少为 p k p_k pk,即 C max ∗ ≥ max { p k : 1 ≤ k ≤ n } C^*_{\text{max}} \geq \max\{p_k : 1 \leq k \leq n\} Cmax∗≥max{pk:1≤k≤n}。
2
设所有工作的总处理时间为 P = ∑ k = 1 n p k P = \sum_{k=1}^{n} p_k P=∑k=1npk。
对于最优调度,每台机器在总时间 C max ∗ C^*_{\text{max}} Cmax∗ 内处理一部分工作。
由于共有 m m m 台机器,总的工作负载 P P P 必须分配给这 m m m 台机器。因此,平均每台机器的负载为 P m \frac{P}{m} mP。
在最优调度中,任意机器的完工时间不能少于其分配到的工作负载时间,即最优完工时间 C max ∗ C^*_{\text{max}} Cmax∗ 不能小于平均机器负载 P m \frac{P}{m} mP,即 C max ∗ ≥ 1 m ∑ k = 1 n p k C^*_{\text{max}} \geq \frac{1}{m} \sum_{k=1}^{n} p_k Cmax∗≥m1∑k=1npk。
3
def GreedyParallelScheduling(jobs, m):# jobs 是一个由元组 (p_k, job_id) 组成的作业列表# m 是机器的数量# 初始化了一个大小为m的空列表schedules,# 用于记录每台机器分配的作业schedules = [[] for _ in range(m)]# 初始化了一个大小为m的数组machine_completion_times,# 用于记录每台机器的完工时间,初始值为0machine_completion_times = [0] * m# 对作业列表按照处理时间的非递增顺序进行排序jobs.sort(reverse=True, key=lambda x: x[0])# 对每个已排序的作业进行调度for (p_k, job_id) in jobs:# 找到完工时间最小的机器 Mimin_machine = machine_completion_times.index(min(machine_completion_times))# 将作业分配给机器 Mischedules[min_machine].append(job_id)# 更新机器 Mi 的完工时间,增加该作业的处理时间machine_completion_times[min_machine] += p_kreturn schedules
运行时间:
- 初始化和读取输入需要 O ( n ) O(n) O(n) 时间。
- 对作业按处理时间排序需要 O ( n log n ) O(n \log n) O(nlogn) 时间。
- 遍历每个作业并找到具有最小结束时间的机器需要 O ( n log m ) O(n \log m) O(nlogm) 时间,因为可以使用最小堆来跟踪机器的结束时间。
总体运行时间为 O ( n log n + n log m ) = O ( n log n ) O(n \log n + n \log m) = O(n \log n) O(nlogn+nlogm)=O(nlogn),因为通常情况下 n ≥ m n \geq m n≥m。
4
设所有工作的总处理时间为 P = ∑ k = 1 n p k P = \sum_{k=1}^{n} p_k P=∑k=1npk,处理时间最长的工作为 p max = max { p k : 1 ≤ k ≤ n } p_{\text{max}} = \max\{p_k : 1 \leq k \leq n\} pmax=max{pk:1≤k≤n}。
在贪心算法中,任何时刻将未分配的工作分配给当前空闲时间最少的机器,这种策略确保每台机器的负载是尽可能均衡的。
假设最坏情况下某台机器上的负载时间为 L L L,即 L ≤ P m + p max L \leq \frac{P}{m} + p_{\text{max}} L≤mP+pmax
其中, P m \frac{P}{m} mP 是平均每台机器分配到的负载时间, p m a x p_{max} pmax 是任何单个工作可能增加的最大负载时间。
因此,贪心算法的完工时间 C m a x C_{max} Cmax 满足
C max ≤ 1 m ∑ k = 1 n p k + max { p k : 1 ≤ k ≤ n } C_{\text{max}} \leq \frac{1}{m} \sum_{k=1}^{n} p_k + \max\{p_k : 1 \leq k \leq n\} Cmax≤m1k=1∑npk+max{pk:1≤k≤n}
由于最优完工时间 C m a x ∗ C^*_{max} Cmax∗ 至少为这两个量中的最大值,即:
C m a x ∗ ≥ max ( 1 m ∑ k = 1 n p k , max { p k : 1 ≤ k ≤ n } ) C^*_{max} \geq \max \left(\frac{1}{m} \sum_{k=1}^{n} p_k, \max\{p_k : 1 \leq k \leq n\}\right) Cmax∗≥max(m1k=1∑npk,max{pk:1≤k≤n})
结合以上两个不等式,可得
C m a x ≤ 2 C m a x ∗ C_{max} \leq 2C^*_{max} Cmax≤2Cmax∗
因此,贪心算法是一个多项式时间的 2-近似算法。
相关文章:

算法 Hw9
Hw 9 1 Scheduling with profits and deadlines12345 2 Parallel machine1234 1 Scheduling with profits and deadlines 1 决策问题表述: 给定一个利润值 P P P,是否存在一个任务调度方案使得完成所有任务的总利润至少为 P P P 2 在 NP 类中&…...
前端JS必用工具【js-tool-big-box】学习,字符串字母大小写转换的方法使用
这一小节,我们说一下 js-tool-big-box 工具库中,字符串字母大小写转换的使用。请注意:不是说单纯的把字符串转为大写,或者小写。关注 js-tool-big-box 的小伙伴可能知道,我们并没有把一些特别基础的,JS原生…...

Zookeeper:分布式系统中的协调者
Zookeeper:分布式系统中的协调者 前言:引言Zookeeper是什么? 基本概念Zookeeper 数据模型Znode 类型会话Watcher 应用场景分布式锁配置维护组服务名字服务 典型应用场景数据发布/订阅负载均衡命名服务分布式协调/通知集群管理Master选举 工作…...

如何使用代理IP进行数据抓取,PHP爬虫抓取京东商品数据
使用代理IP进行数据抓取通常是为了绕过IP封锁、提高抓取效率或保护你的真实IP地址。在PHP中,你可以使用cURL库来发送HTTP请求,并通过设置cURL选项来使用代理IP。 以下是一个基本的步骤说明,展示如何使用PHP和cURL库结合代理IP来抓取京东商品…...
一口气安装【Python】教程
浏览器搜索python,或者直接跳转网址。 https://www.python.orghttps://www.python.org/ 找到想下载的版本 根据自己电脑下载相应的版本 自定义安装 下一步 修改路径,然后点击安装 等待一会,喝个饮料 点击关闭 安装成功 安装结束...

华为HCIP Datacom H12-821 卷13
1.多选题 以下关于二层漫游和三层漫游的描述,以下说法正确的是? A、如果 STA 漫游时前后关联的 VLAN ID 相同则一定属于二层漫游 B、二层漫游是指客户端在同一子网内漫游 C、三层漫游是指客户端在不同子网间漫游 D、三层漫游前后 STA 关联的 AP 服务集上的 VL AN 必须相…...
基于SSM的酒店客房管理系统
基于SSM的酒店客房管理系统 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅获取项目下载方式🍅 链接点击直达:下载…...
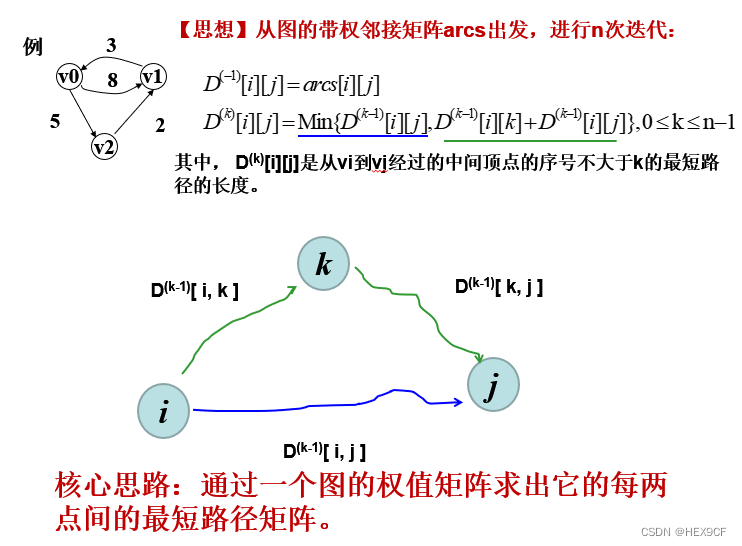
【数据结构与算法】最短路径,Floyd算法,Dijkstra算法 详解
Floyd算法 for (int k 0; k < n; k) {for (int i 0; i < n; i) {for (int j 0; j < n; j) {if (d[i][k] ! INF && d[k][j] ! INF) {d[i][j] min(d[i][j], d[i][k] d[k][j]);}}} }Dijkstra算法(基于最小堆) void dijkstra(int st…...

PHP中如何进行网络爬虫和数据抓取?
随着互联网时代的到来,网络数据的爬取与抓取已成为许多人的日常工作。在支持网页开发的程序语言中,php以其可扩展性和易上手的特点,成为了网络爬虫和数据抓取的热门选项。本文将从以下几个方面介绍php中如何进行网络爬虫和数据抓取。 一、HT…...
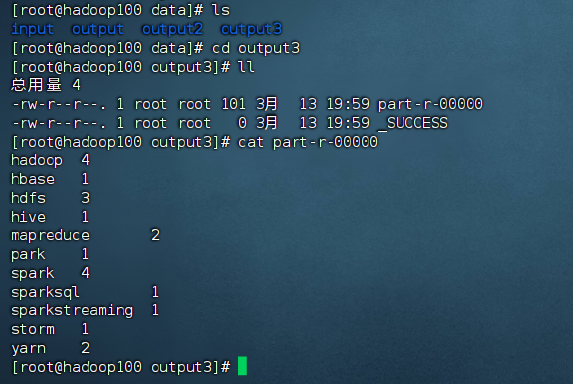
【Hadoop集群搭建】实验3:JDK安装及配置、Hadoop本地模式部署及测试
1. 安装 SSH 工具 SSH Secure Shell Client 传输软件 FinalShell(推荐使用) 1.1使用SSH工具将JDK安装包上传至虚拟主机hadoop01, hadoop02, hadoop03,sogou500w 数据上传至 hadoop01。 a. 在虚拟主机/usr 目录下创建文件夹 java,JDK 上传至此目录&…...

分布式锁在Spring Boot应用中的优雅实现
在现代微服务架构中,分布式锁是一种常用的技术手段,用于确保在分布式系统中,同一时间只有一个服务实例能够执行某个特定的操作。这对于防止并发问题、保证数据一致性至关重要。在Spring Boot应用中,我们可以通过自定义注解和切面的…...

常用框架-Spring Boot
常用框架-Spring Boot 1、Spring Boot是什么?2、为什么要使用Spring Boot?3、Spring Boot的核心注解是哪个?它主要由哪几个注解组成的?4、有哪些运行Spring Boot的方式?5、如何理解 Spring Boot 中的Starters?6、有哪些常见的Starters?7、如何在Spring Boot启动的时候运…...

AttributeError: module ‘cv2‘ has no attribute ‘face‘
Traceback (most recent call last): File "D:\AI_37\pythonProject7\day23\课堂代码\day23\07-人脸识别.py", line 4, in <module> recognizer cv2.face.LBPHFaceRecognizer_create() ^^^^^^^^ AttributeError: module cv2 has no at…...

不管你是普本还是双一流,建议你一定要尝试一下学习GIS开发
毕业季,很多企业的秋招和暑期实习已经开始了,在这个24秋招和25考研并列进行的毕业季,GIS专业的同学,做好自己的职业规划显得十分重要。 WebGIS开发,近年来成为了3S及相关专业的学生备受关注的热门选择。 不论是本科毕…...

OurBMC大咖说丨第5期:BMC开发中的非标准化问题探讨
栏目介绍:"OurBMC大咖说" 是由 OurBMC 社区精心策划的线上讲座栏目,邀请 BMC 相关领域大咖共同探讨 BMC 全栈技术的发展趋势、挑战和机遇。无论你是初学者还是资深从业者,"OurBMC大咖说" 都将为你提供一个宝贵的学习和交…...

空调制冷剂泄漏引发健康隐患,冷媒传感器实时监测至关重要
随着夏季的脚步逐渐临近,气温逐渐攀升,空调成为了许多家庭和企业必不可少的降温设备。然而,近年来多起因空调制冷剂泄漏导致的健康问题和安全事故,让人们开始重新审视空调使用安全的重要性。其中,冷媒传感器的实时监测…...

开源TinyFSM状态机适用于嵌入式工业平台吗?
文章目录 引言基于传统 C 实现的状态机TinyFSM 实现的对比现代 C 实现的状态机性能对比TinyFSM 性能测试传统 C 性能测试现代 C 性能测试 工业Misra C编程标准TinyFSM 的优缺点分析结论 引言 TinyFSM是一个为C设计的轻量级有限状态机开源库库。 在嵌入式系统开发中,…...
EE trade:利弗莫尔三步建仓法
在股市投资领域,利弗莫尔这个名字代表着无数的智慧和经历。他的三步建仓法成为了投资者们趋之若鹜的学习对象。本文将详细解析利弗莫尔的著名买入法,通过分步进攻方式,有效掌控市场并实现盈利。 一、利弗莫尔的三步建仓法详解 利弗莫尔三步…...

Java中Callable的应用
在Java中,Callable接口是一种用于并发编程的接口,它与Runnable类似,但有一些重要的区别和优势。Callable接口提供了一种在多线程环境下执行任务并返回结果的方法。以下是一些Callable接口的常见应用场景和使用示例: Callable vs.…...
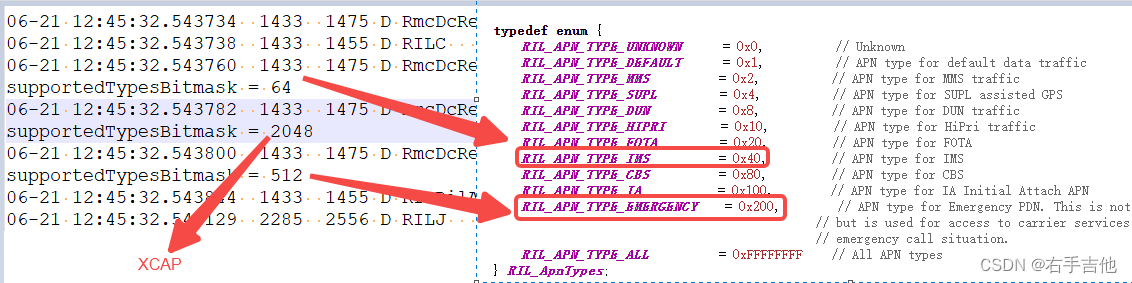
测试卡无法仪表注册问题分析
1、问题描述 00101测试卡无法注册LTE网络,modemlog中发现终端未发起Attach请求,对比正常注册非正常注册的版本,发现正常的多出了ims apn。可以通过ATCGDCONT?来查询modem APN参数。 2、问题分析 目前Modem是一套,没有相关修改。因…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...
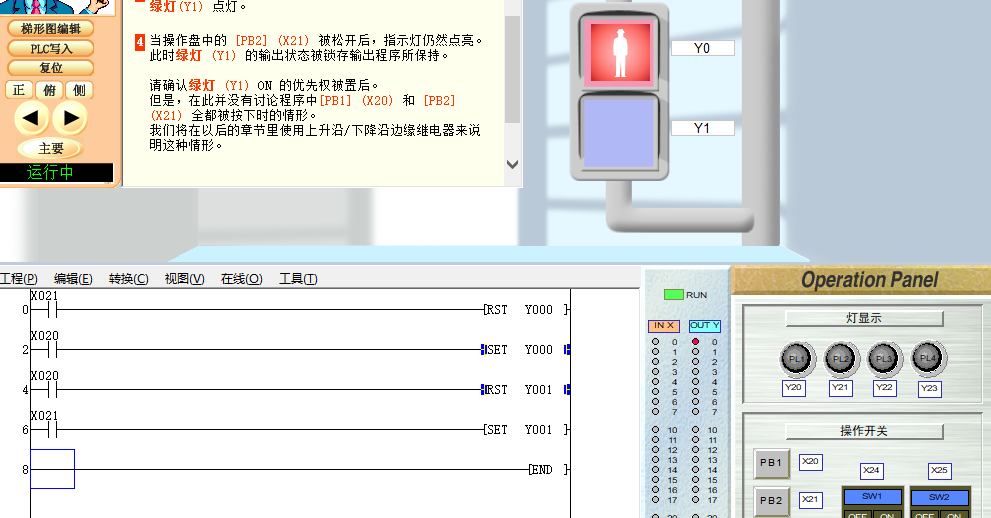
PLC入门【4】基本指令2(SET RST)
04 基本指令2 PLC编程第四课基本指令(2) 1、运用上接课所学的基本指令完成个简单的实例编程。 2、学习SET--置位指令 3、RST--复位指令 打开软件(FX-TRN-BEG-C),从 文件 - 主画面,“B: 让我们学习基本的”- “B-3.控制优先程序”。 点击“梯形图编辑”…...

调试快捷键 pycharm vscode
目录 调试快捷键 pycharm vscode 修改快捷键 方法 1:通过菜单打开 方法 2:用快捷键打开 调试快捷键 pycharm Resume Program F9 Step Over F8 两个离的比较近,比较方便,比vscode的好。 vscode Continue F5 改为F9 S…...

Qt Quick模块功能及架构
Qt 6.0 中的 Qt Quick 模块是构建现代、动态用户界面的核心框架,基于声明式编程(QML)和 JavaScript,专注于高性能、流畅的动画和跨平台 UI 开发。、 一、主要功能改进 1. Qt Quick 核心架构 QML 引擎升级:Qt 6.0 使用…...
