epoch和batch的区别
在机器学习和深度学习中,“epoch”(批次)和"batch"(批量)是两个重要的概念,它们分别表示训练过程中的不同阶段和数据处理方式。
Epoch(批次)
- 定义:Epoch(批次)指的是整个训练数据集被送入神经网络中,并且被用于更新参数一次的过程。简单来说,一个 epoch 表示神经网络训练时所有训练数据通过网络一次,用于参数的更新。
- 意义:完成一个 epoch 后,整个数据集中的所有样本都参与了一次训练,用于计算损失函数、计算梯度并更新模型的参数。通常情况下,训练过程会通过多个 epoch 来提高模型的性能,直到达到预定的停止条件(如收敛)。
Batch(批量)
- 定义:Batch(批量)是指在一个 epoch 中,为了加速训练过程,将大规模的数据集分成若干个较小的块进行训练。每个 batch 包含一定数量的样本数据。
- 意义:通过使用 batch,可以减少每次参数更新的计算量,提高计算效率。在每个 batch 中,模型会根据这些样本的损失函数计算梯度并更新参数。通常情况下,一个 batch 中的样本数目称为 batch size。
区别总结
- Epoch 是训练过程中的一个单位,指的是所有训练数据被送入模型并进行了一次前向传播和一次反向传播的过程。
- Batch 是在一个 epoch 中,为了提高计算效率和减少内存消耗而将数据分成的小块,每个块中包含的样本数量即为 batch size。
示例理解:
- 如果你的训练数据集有 1000 个样本,你设定的 batch size 是 50,那么在一个 epoch 中会有 1000/50=20 个 batch。
- 在训练过程中,会连续地用每个 batch 中的数据计算梯度并更新模型参数,直到完成一个 epoch。
相关文章:

epoch和batch的区别
在机器学习和深度学习中,“epoch”(批次)和"batch"(批量)是两个重要的概念,它们分别表示训练过程中的不同阶段和数据处理方式。 Epoch(批次) 定义:Epoch&…...

非递归创建二叉查找树
非递归创建二叉查找树代码。 #include <stdio.h> #include <stdlib.h>typedef int KeyType; typedef struct BSTNode{KeyType key;struct BSTNode *lchild,*rchild; }BSTNode,*BiTree;//王道书上的递归写法,代码简单,但是理解有难度 //int …...

摄影师危!AI绘画即将降维打击摄影行业
你还以为AI绘画影响的只是插画师行业吗?错了,摄影行业也即将面临技术洗牌 话不多说,先看一下这几张图 你能一眼看出这是AI画的迪丽热巴吗? 你是不是还以为AI绘画只能画点动漫艺术风格?那你就低估了AI的发展速度&…...

ts 中class
class obj{name:stringage:numberconstructor(name:string,age:number){this.name namethis.age age}setname(){this.name 111 } } //新建实例 //构造方法中的this指向调用者,谁new就指向谁 //这个this 指向 o,打印this,可以获取到o身上的…...
Dledger框架日志同步流程)
深度解析RocketMq源码-高可用存储组件(四)Dledger框架日志同步流程
1.绪论 在深度解析RocketMq源码-高可用存储组件(一) raft协议详解-CSDN博客 中讲过,raft协议中,日志同步主要有两个地方,一个是leader会跟follower同步数据,另一个是在新leader诞生的时候,会与…...
ONLYOFFICE 文档开发者版 8.1:API 更新
随着版本 8.1 新功能的发布,我们更新了编辑器、文档生成器和插件的 API,并添加了 Office API 板块。阅读下文了解详情。 ONLYOFFICE 文档是什么 ONLYOFFICE 文档是一个功能强大的文档编辑器,支持处理文本文档、电子表格、演示文稿、可填写…...

Activemq单节点在Windows下的配置部署
1.环境信息 服务器信息jdk版本activemq版本备注Windows Server 2008R2 Enterprisejdk-17_windows-x64_bin.exeapache-activemq-5.18.42.jdk配置 1.下载jdk 地址: Java Downloads | Oracle 中国 2.上传至Windows服务器,点击安装,在选择安装目录页面,选择合适的安装目录即…...
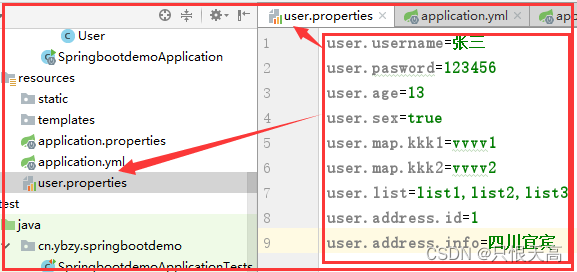
SpringBoot-注解@ImportResource引入自定义spring的配置xml文件和配置类
1、注解ImportResource 我们知道Spring的配置文件是可以有很多个的,我们在web.xml中如下配置就可以引入它们: SprongBoot默认已经给我们配置好了Spring,它的内部相当于已经有一个配置文件,那么我们想要添加新的配置文件怎么办&am…...

GitLab配置免密登录之后仍然需要Git登录的解决办法
GitLab配置免密登录之后仍然需要Git登录的解决办法 因为实习工作需要,要在本地拉取gitlab上的代码,设置了密钥之后连接的时候还需要登录的token,摸索之后有了下面的解决办法。 方法一: 根据报错的提示,去网站上设置个人…...

探索小众爱好:打造个人韧性与特色之路
在这个信息爆炸的时代,我们很容易陷入“千篇一律”的漩涡中,无论是生活方式还是兴趣爱好,似乎都趋向于某种“流行”或“热门”。然而,真正的个性与魅力,往往来源于那些不为大众所知的小众爱好。今天,我想和…...
)
GitHub使用教程(小白版)
看一百篇文章不如自己写一篇 第一步:注册和安装 注册GitHub账号 访问 GitHub官网。点击右上角的 "Sign up" 按钮。按照提示输入你的邮箱、创建用户名和密码,完成注册。 安装Git 访问 Git官网。下载并安装适用于你操作系统的Git。安装…...

深度解析SD-WAN在企业组网中的应用场景
在现代企业快速发展的网络环境中,SD-WAN技术不仅是实现企业各站点间高效连接的关键,也是满足不同站点对互联网、SaaS云应用和公有云等多种业务需求的理想选择。本文将从企业的WAN业务需求出发,对SD-WAN的组网场景进行全面解析,涵盖…...
】Eclipse Nios II SBT 无法从模板创建新应用程序和 BSP)
【INTEL(ALTERA)】Eclipse Nios II SBT 无法从模板创建新应用程序和 BSP
目录 说明 解决方法 说明 您应该能够创建新的应用程序和 BSP 模板包含以下步骤: 选择 Nios II应用程序和 BSP 来自模板。选择您的.sopcinfo 文件并选择模板。从您的工作区单击 选择现有的 BSP 项目。单击 创建。选择所需的 BSP 选项。单击 完成。 但是…...
Vue_cli搭建过程项目创建
概述 vue-cli 官方提供的一个脚手架,用于快速生成一个 vue 的项目模板;预先定义 好的目录结构及基础代码,就好比咱们在创建 Maven 项目时可以选择创建一个 骨架项目,这个骨架项目就是脚手架,我们的开发更加的快速&am…...
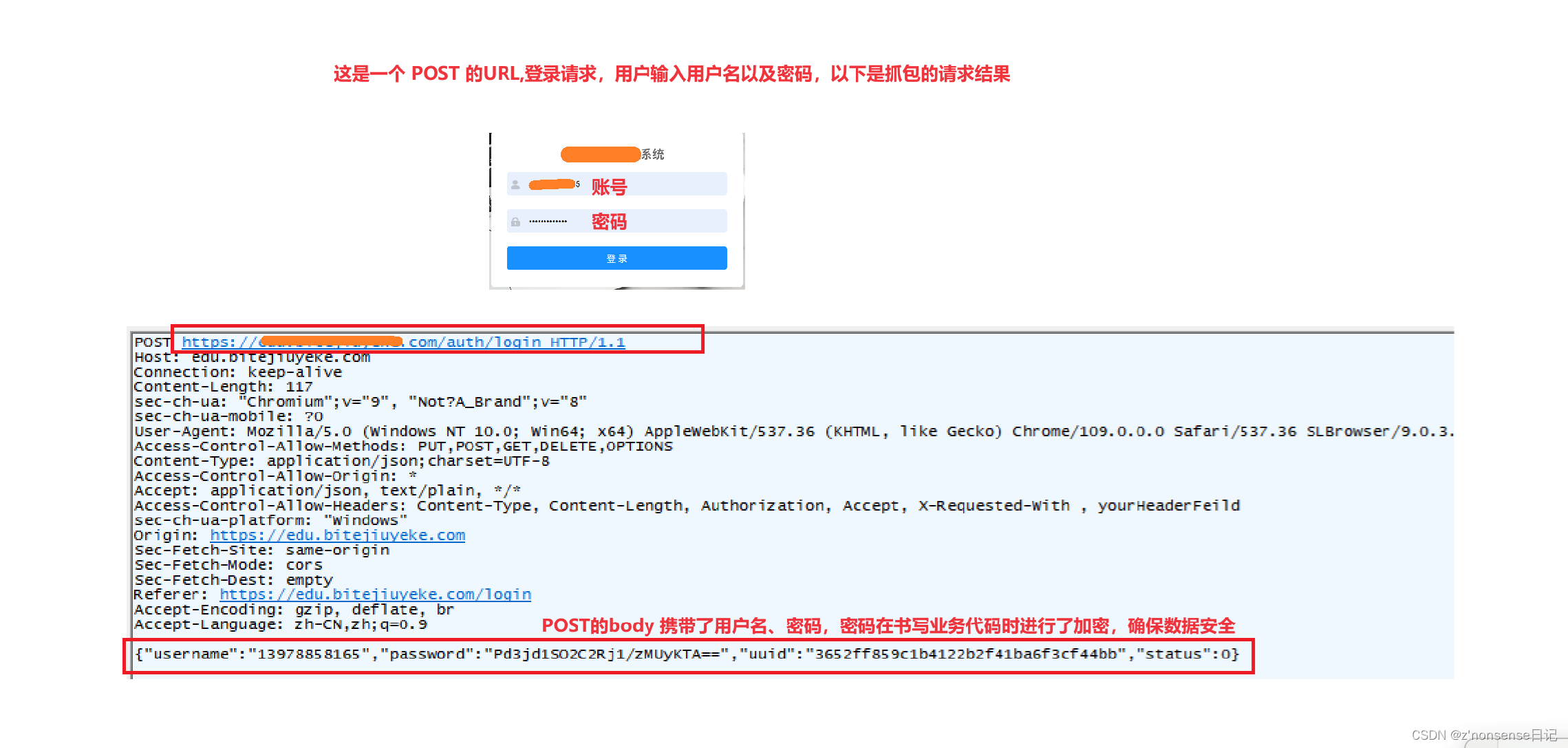
面试题4:POST 比 GET 安全?
不是。HTTP就没有加密功能。 我们知道 GET一般将参数放到URL的查询字符串中,如果是实现登录页面,我们的用户名和密码就直接显示到浏览器的地址栏中了,此时就会轻易的被他人获取账号密码,很不安全。而POST会把参数放到 body 里&am…...
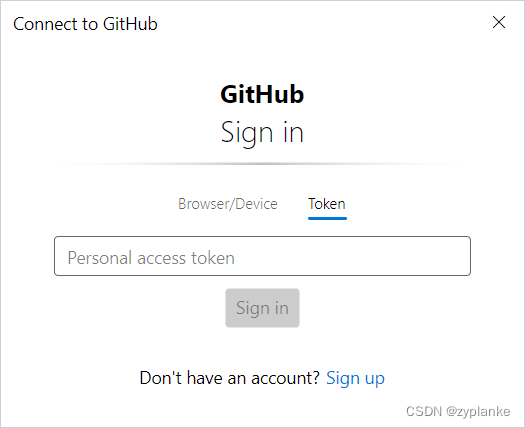
Github生成Personal access tokens及在git中使用
目录 生成Token 使用Token-手工修改 使用Token-自动 生成Token 登录GitHub,在GitHub右上角点击个人资料头像,点击Settings → Developer Settings → Personal access tokens (classic)。 在界面上选择点击【Generate new token】,填写如…...

【BUG记录】条件查询没有查询结果 || MybatisPlus打印查询语句
结论 先说结论,查询没有结果,可能是数据库连接,数据问题之类,最有可能的根本原因是查询语句问题,需要想办法检查查询语句,使用mybatisPlus等自动生成查询语句的框架不能直接看语句,可以依靠日志…...
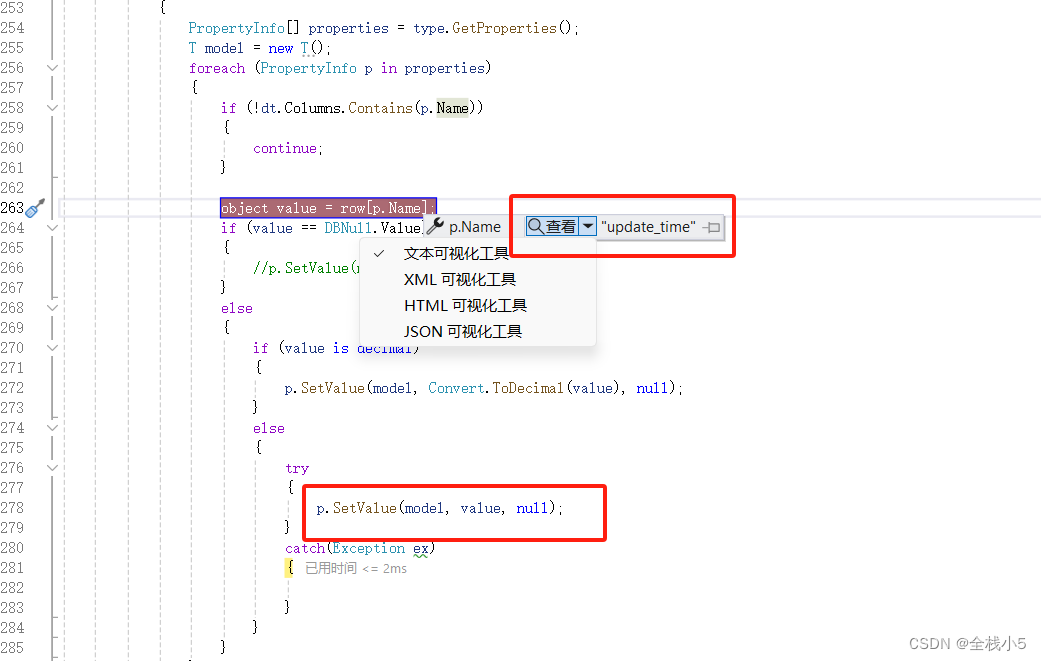
【C#】找不到属性集方法。get只读属性用了反射设置setValue肯定报错
欢迎来到《小5讲堂》 这是《C#》系列文章,每篇文章将以博主理解的角度展开讲解。 温馨提示:博主能力有限,理解水平有限,若有不对之处望指正! 背景 找不到属性集方法。get只读属性用了反射设置setValue肯定报错 报错…...
探索ChatGPT在程序员日常工作的多种应用
引言 在现代科技迅猛发展的今天,人工智能的应用已经深入到我们生活和工作的各个方面。作为程序员,我们时常面临大量繁杂的任务,从代码编写、错误调试到项目管理和团队协作,每一项都需要花费大量的时间和精力。近年来,…...

算法与数据结构——时间复杂度详解与示例(C#,C++)
文章目录 1. 算法与数据结构概述2. 时间复杂度基本概念3. 时间复杂度分析方法4. 不同数据结构的时间复杂度示例5. 如何通过算法优化来提高时间复杂度6. C#中的时间复杂度示例7. 总结 算法与数据结构是计算机科学的核心,它们共同决定了程序的性能和效率。在实际开发中…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
