代码随想录算法训练营Day50|1143.最长公共子序列、1035.不相交的线、53.最大子序和、392.判断子序列
最长公共子序列
1143. 最长公共子序列 - 力扣(LeetCode)
代码随想录 (programmercarl.com)
最长公共子序列 - 动态规划 Longest Common Subsequence - Dynamic Programming_哔哩哔哩_bilibili
本题和上一题718.最长重复子数组在很多方面相似,区别在与不需要连续,因此在dp数组的推导上有些改变。
由于不需要连续,dp[i][j]的值针对text1和text2相同及不同这两种情况有不同的表示。
首先 dp[i][j]表示序列text1[0:i-1]和text2[0:j-1]的最长公共子序列的长度
当text[i-1] == text[j-1]时,dp[i][j] = dp[i-1][j-1]+1,而当text1[i-1]!=text2[j-1]时,dp[i][j] = max(dp[i-1][j],dp[i][j-1]),dp[i][j]由数组左和上的较大值确定。
由此,dp[i][j]由左上部分确认,当i j为0时,表示的序列为空,空序列与任何序列的最长公共子序列均为空,长度为0,dp[0][0]、dp[0][1]、dp[1][0]都为0。
i,j两个变量循环遍历。
最后返回dp[text1.size()][text2.size()]。
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {// 创建一个二维向量 dp,用于存储动态规划的状态值// dp[i][j] 表示 text1 的前 i 个字符和 text2 的前 j 个字符的 LCS 长度// 初始化 dp 的大小为 (text1.size()+1) x (text2.size()+1),值全部为 0vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));// 双层循环遍历 text1 和 text2for (int i = 1; i <= text1.size(); i++) { // i 从 1 开始,直到 text1.size()for (int j = 1; j <= text2.size(); j++) { // j 从 1 开始,直到 text2.size()// 如果 text1 的第 i 个字符和 text2 的第 j 个字符相同if (text1[i - 1] == text2[j - 1]) {// 则 dp[i][j] 等于 dp[i-1][j-1] 加 1dp[i][j] = dp[i - 1][j - 1] + 1;} else {// 如果不相同,则 dp[i][j] 等于 dp[i-1][j] 和 dp[i][j-1] 中的较大值// 这意味着当前字符不包含在 LCS 中dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}// 返回 dp[text1.size()][text2.size()],即 text1 和 text2 的 LCS 长度return dp[text1.size()][text2.size()];}算法的时间复杂度为O(m*n),空间复杂度为O(m*n),m和n分别代表两个序列的长度,二维数组,二维循环遍历。
不相交的线
1035. 不相交的线 - 力扣(LeetCode)
和上题一致,换些变量便能解决,不过真要面试的时候,希望能想到吧。
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {// 创建一个二维向量 dp,用于存储动态规划的状态值// dp[i][j] 表示 nums1 的前 i 个元素和 nums2 的前 j 个元素的最长公共子序列的长度// 初始化 dp 的大小为 (nums1.size()+1) x (nums2.size()+1),值全部为 0vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));// 双层循环遍历 nums1 和 nums2for (int i = 1; i <= nums1.size(); i++) { // i 从 1 开始,直到 nums1.size()for (int j = 1; j <= nums2.size(); j++) { // j 从 1 开始,直到 nums2.size()// 如果 nums1 的第 i 个元素和 nums2 的第 j 个元素相同if (nums1[i - 1] == nums2[j - 1]) {// 则 dp[i][j] 等于 dp[i-1][j-1] 加 1dp[i][j] = dp[i - 1][j - 1] + 1;} else {// 如果不相同,则 dp[i][j] 等于 dp[i-1][j] 和 dp[i][j-1] 中的较大值// 这意味着当前元素不包含在 LCS 中dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}// 返回 dp[nums1.size()][nums2.size()],即 nums1 和 nums2 的 LCS 长度// 这也是不相交的直线段的最大数量return dp[nums1.size()][nums2.size()];}算法的时间复杂度为O(m*n),空间复杂度为O(m*n)。
最大子序和
53. 最大子数组和 - 力扣(LeetCode)
之前用过贪心算法解这道题,当子序和为负,则抛弃当前子序和,从下一个位置开始计算子序和。这里使用动态规划也是类似的。
由于是连续的子序和,dp[i]表示到i为止的最大子序和(此处应包含nums[i])
dp[i] = max(dp[i-1]+nums[i],nums[i]),这里可以想象贪心的思路,当dp[i-1]为负时,自然dp[i-1]+nums[i]要小于nums[i]。
因此,唯一需要的是当前元素的前一位的dp值,dp[0] = nums[0]。
从前往后遍历
最后返回dp数组中的最大值。
class Solution {
public:int maxSubArray(vector<int>& nums) {// 创建一个向量 dp,用于存储以第 i 个元素结尾的最大子数组和// 初始化 dp 的大小与 nums 相同,值全部为 0vector<int> dp(nums.size(), 0);// dp[0] 是数组第一个元素的值,因为一个元素的子数组和就是它本身dp[0] = nums[0];// 遍历数组 nums,从第二个元素开始for (int i = 1; i < nums.size(); i++) {// 如果以第 i-1 个元素结尾的最大子数组和小于 0if (dp[i - 1] < 0) {// 则以第 i 个元素结尾的最大子数组和就是第 i 个元素的值// 因为加上前面的子数组和会使得和更小dp[i] = nums[i];} else {// 如果以第 i-1 个元素结尾的最大子数组和大于等于 0// 则将第 i 个元素的值加到以第 i-1 个元素结尾的最大子数组和上// 这样可以保持子数组的连续性dp[i] = dp[i - 1] + nums[i];}}// 使用 STL 中的 max_element 函数找出 dp 中的最大值// 这个最大值就是整个数组的最大子数组和return *max_element(dp.begin(), dp.end());}
};
算法的时间复杂度为O(n),空间复杂度为O(n)。
判断子序列
392. 判断子序列 - 力扣(LeetCode)
同样和最长公共子序列相似,在遍历过程中,当dp[i][j] == s.size()时,表示s为t的子序列,否则s不是t的子序列,具体代码如下。
class Solution {
public:// 定义一个成员函数,用于判断 s 是否为 t 的子序列bool isSubsequence(string s, string t) {// 如果 s 为空字符串,那么它是任何字符串的子序列if (s.size() == 0) {return true;}// 创建一个二维向量 dp,用于存储动态规划的状态值// dp[i][j] 表示 s 的前 i 个字符和 t 的前 j 个字符的匹配长度vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));// 双层循环遍历 s 和 tfor (int i = 1; i <= s.size(); i++) { // i 从 1 开始,直到 s.size()for (int j = 1; j <= t.size(); j++) { // j 从 1 开始,直到 t.size()// 如果 s 的第 i 个字符和 t 的第 j 个字符相同if (s[i - 1] == t[j - 1]) {// 则 dp[i][j] 等于 dp[i-1][j-1] 加 1dp[i][j] = dp[i - 1][j - 1] + 1;// 如果匹配长度等于 s 的长度,说明 s 是 t 的子序列if (dp[i][j] == s.size()) {return true;}} else {// 如果不相同,则 dp[i][j] 等于 dp[i-1][j] 和 dp[i][j-1] 中的较大值// 这表示当前字符不包含在子序列中dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}// 如果遍历完 dp 数组后没有找到匹配长度等于 s 长度的状态,则 s 不是 t 的子序列return false;}
};
算法的时间复杂度为O(m*n),空间复杂度为O(m*n)。
相关文章:

代码随想录算法训练营Day50|1143.最长公共子序列、1035.不相交的线、53.最大子序和、392.判断子序列
最长公共子序列 1143. 最长公共子序列 - 力扣(LeetCode) 代码随想录 (programmercarl.com) 最长公共子序列 - 动态规划 Longest Common Subsequence - Dynamic Programming_哔哩哔哩_bilibili 本题和上一题718.最长重复子数组在很多方面相似…...
国家自然科学基金标书大全(2002-2024)
数据来源:在20世纪80年代初,为了促进中国的科技体制革新并改革科研资金分配机制,中国科学院的89位院士联名向党和国家领导人提出建议,设立了国家自然科学基金的设立。国自然基金自创立以来,根据国家发展科学技术方针、…...

Python代码打包成exe应用
目录 一、前期准备 二、Pyinstaller打包步骤 Pyinstaller参数详解 三、测试 Spec 文件相关命令 一、前期准备 (1)首先,我们需要确保你的代码可以在本地电脑上的pycharm正常运行成功。 (2)我们要先安装Pyinstalle…...
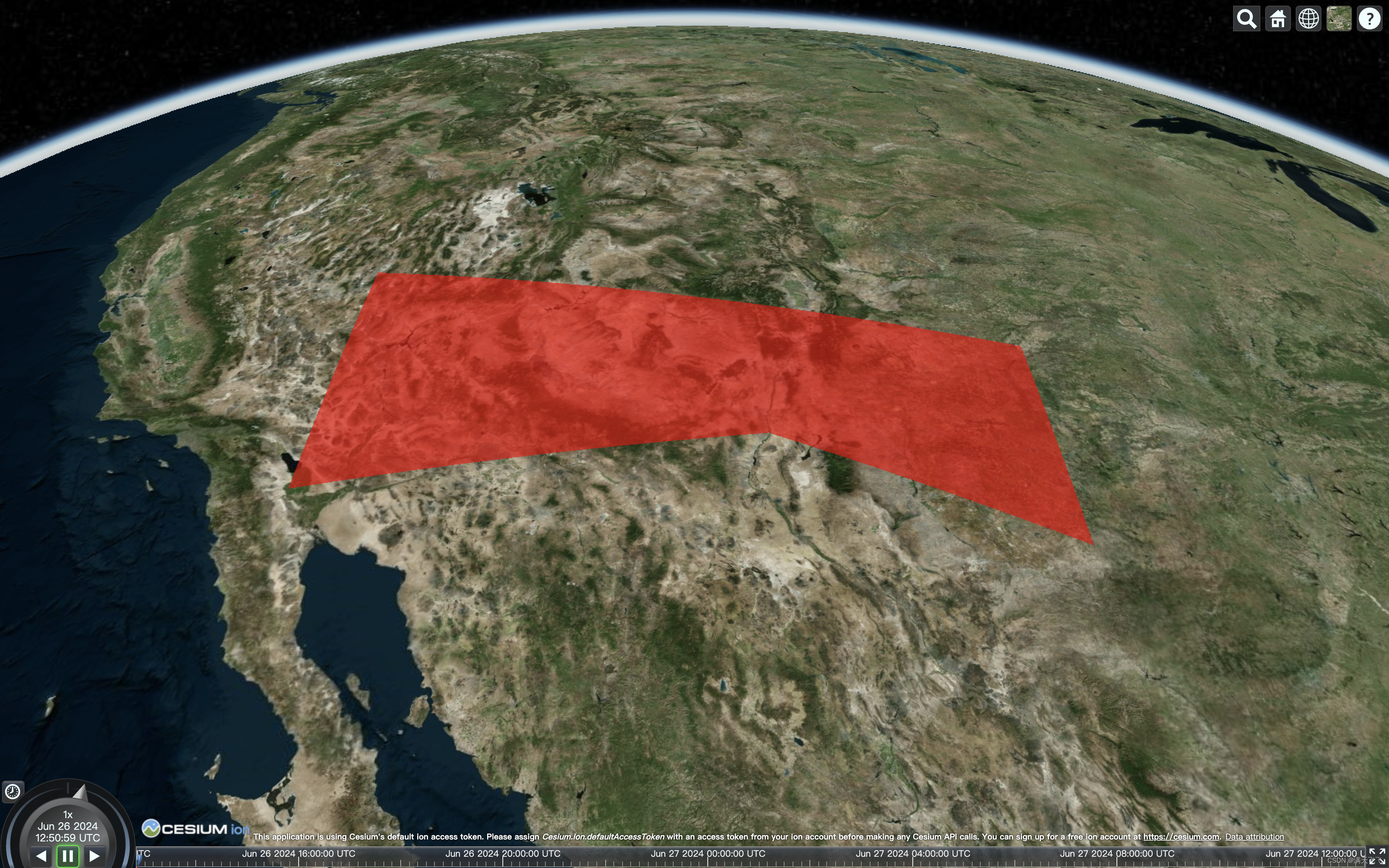
CesiumJS【Basic】- #016 多边形面渲染“花了”的问题
文章目录 多边形面渲染“花了”的问题1 目标2 问题代码3 修正后代码4 总结多边形面渲染“花了”的问题 1 目标 解决多边形的面“花了”的问题 2 问题代码 使用Cesium.PerInstanceColorAppearance渲染后出现色斑 import * as Cesium from "cesium";const viewer …...

qt 开发对信号槽进行二次封装,实现信号槽管理接口。
最近做的一个项目,由于工程需要模块之间能够互相通信,但又不想模块之间耦合度太高 使用信号槽的话,需要两个类的对象或者指针在其中一个类都要体现,这样达不到效果, 想要一个管理类对这些互相通信的类之间进行管理,只需要在各自的类注册发送者和接收者即可,双方通过一…...
本地项目上传到gitee
本地项目通过webstorm上传到gitee 1.登录gitee选择新建仓库 2.输入新建仓库的名字(名字与本地项目名一致) 3.复制链接 4.找到本地项目,选中地址输入cmd打开命令提示框 5.输入git init初始化git,生成.git文件 6.webstorm中打开项目…...
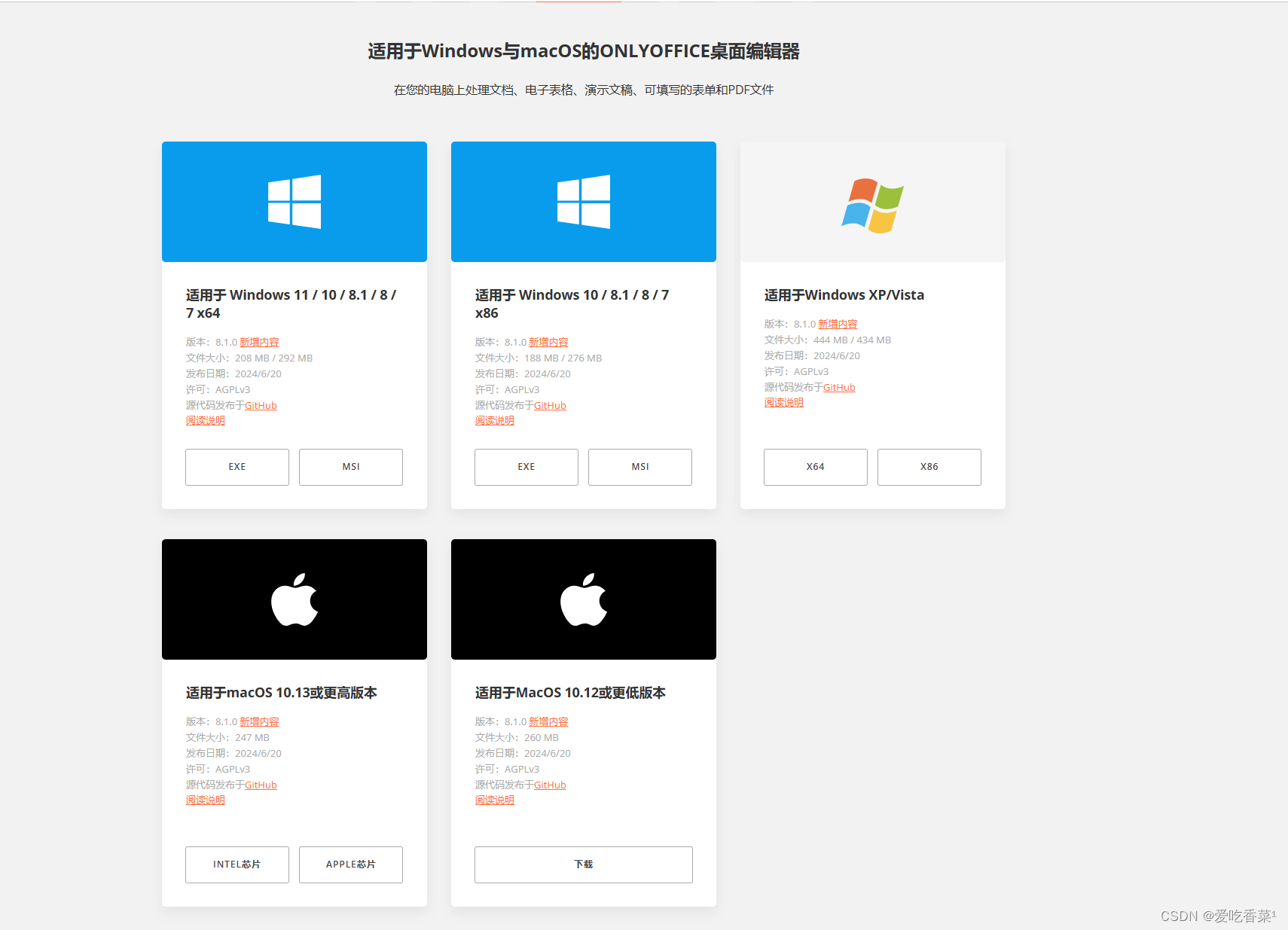
ONLYOFFICE 8.1版本桌面编辑器测评:超越想象的办公体验!
在当今数字化办公时代,一个功能强大、操作便捷的办公套件对于提高工作效率至关重要。ONLYOFFICE 8.1作为一款备受瞩目的办公软件,凭借其全面的功能、优异的性能和出色的用户体验,为用户带来了超越想象的办公体验。下面,我们将对ON…...

中介子方程三十四
XXFXXuXXWXXuXXdXXrXXαXXuXpXXKXηXiXXαXXiXηXKXXpXuXXαXXrXXdXXuXWXπXXWXeXyXeXbXπXpXXNXXqXeXXrXXαXXuXpXXKXηXiXXαXXiXηXKXXpXuXXαXXrXXeXqXXNXXpXπXbXeXyXeXWXXπXWXuXXdXXrXXαXXuXpXXKXηXiXXαXXiXηXKXXpXuXXαXXrXXdXXuXXWXXuXXFXXEXXyXXEXXrXXαXXuXpXXK…...
最新Sublime Text软件安装包分享(汉化版本)
Sublime Text 是一款广受欢迎的跨平台文本编辑器,专为代码、标记和散文编辑而设计。它以其简洁的用户界面、强大的功能和高性能而著称,深受开发者和写作者的喜爱。 一、下载地址 链接:https://pan.baidu.com/s/1kErSkvc7WnML7fljQZlcOg?pwdk…...
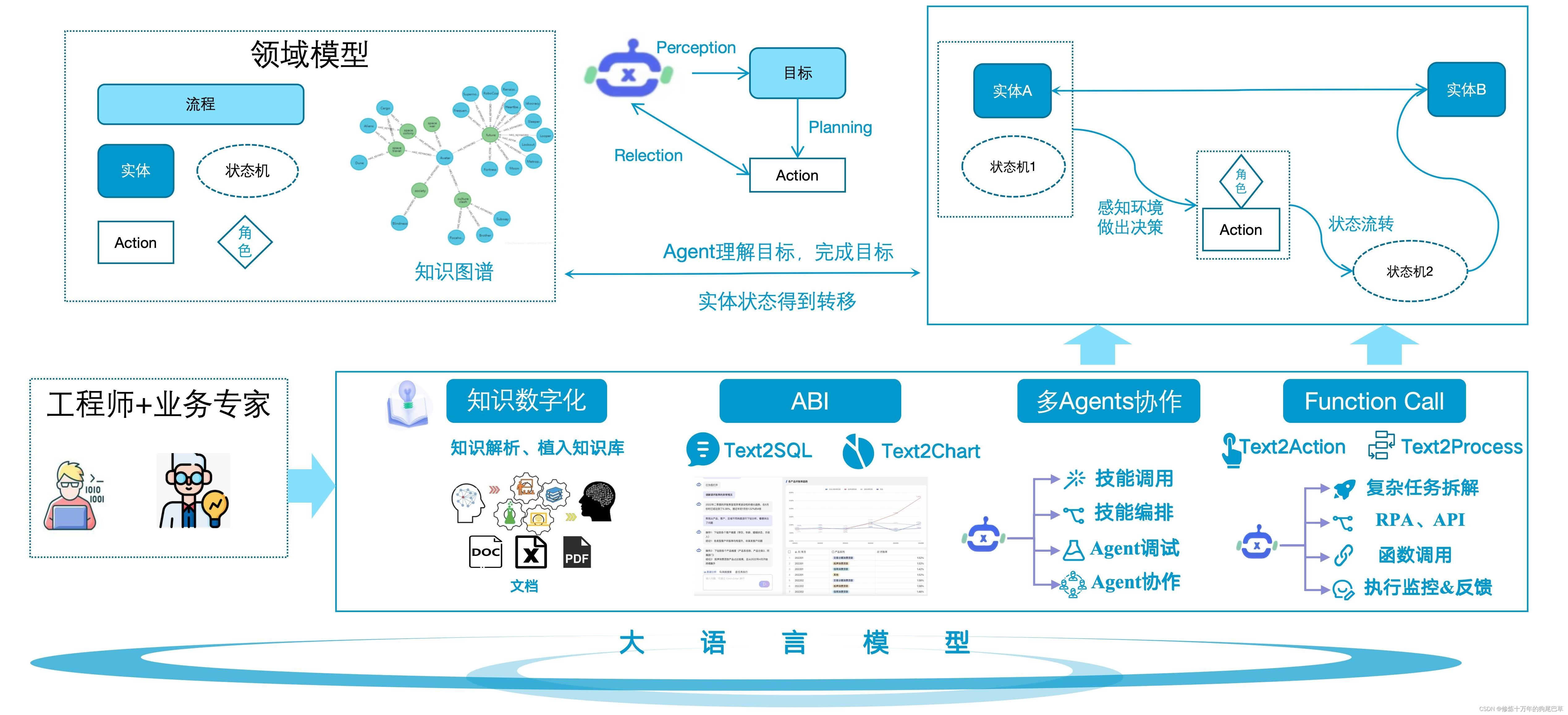
AI-智能体基础设施
个性化记忆需要世界模型来协助构建 业界有一个精简的Agent表达公示,即:Agent大模型(LLM)记忆(Memory)主动规划(Planning)工具使用(Tool Use)。基于该公式&am…...

【docker】docker启动neo4j,并配置内存
注意下:--volume宿主机目录:/data 和 --publish宿主机port:7474 --publish宿主机port:7687 docker run -d \ --publish9801:7474 --publish9802:7687 \ --env NEO4J_AUTHneo4j/passwd \ --volume/opt/docker/data/vol-data/neo4j4.2:/data \ --restart always \ --…...

面试准备记录
6月26日 今日学习 MySQL的1-7题(中期报告,加上玩了游戏,就没有认真背题) 6月25日 今日复习 JVM的内存管理部分(1-31题) 6月24日 今日学习 类的生命周期?类加载过程?类加载器有…...
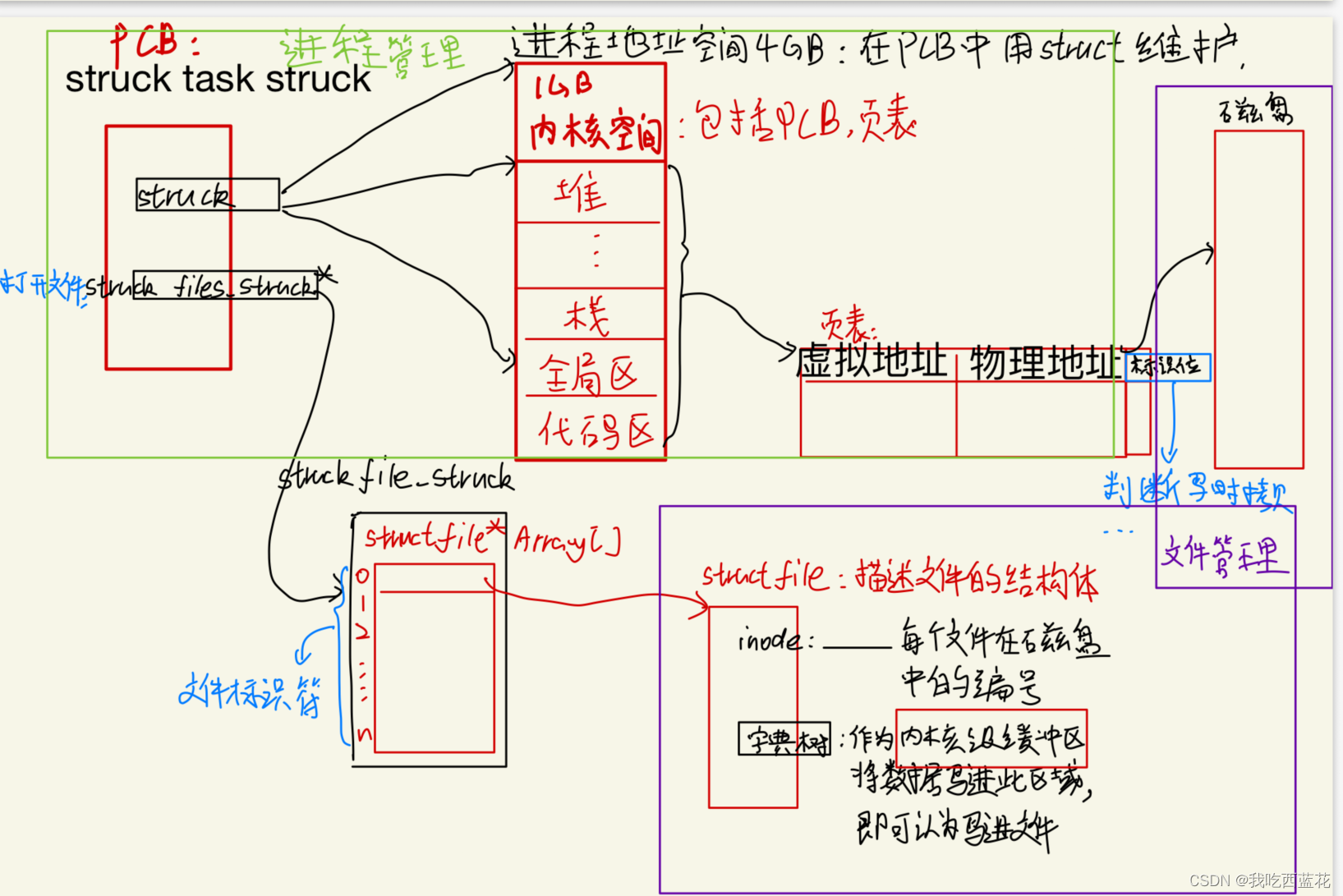
文件管理—linux(基础IO)
目录 编辑 一、C语言文件接口(库函数) hello.c写文件 hello.c读文件 输出信息到显示器 stdin & stdout & stderr 二、系统文件I/O(系统调用) hello.c 写文件: hello.c读文件 接口介绍 open open…...

【华为OD机试|01】最远足迹(Java/C/Py/JS)
目录 一、题目介绍 1.1 题目描述 1.2 备注: 1.3 输入描述 1.4 输出描述 1.5 用例 二、Java代码实现 2.1 实现思路 2.2 详细代码 2.3 代码讲解: 三、C语言实现 3.1实现步骤 3.2 实现代码 3.3 代码详解 四、Python实现 4.1 实现步骤 4.2 …...

conda安装管理配置
原文链接:conda管理配置 导言 安装卸载 卸载 卸载 docker sudo rm -r /opt/anaconda3 #conda安装位置安装 从镜像archive中下载sh脚本安装 bash ./software/Anaconda3-2024.02-1-Linux-x86_64.sh -b -p /opt/anaconda3 #conda安装位置管理 查看 conda --ver…...

鸿蒙开发HarmonyOS NEXT(一)
最近总听见大家讨论鸿蒙,前端转型的好方向?先入门学习下 目前官方版本和文档持续更新中 一、开发环境 提示:要占用的空间比较多,建议安装在剩余空间多的盘 1、下载:官网最新工具 - 下载中心 - 华为开发者联盟 (huaw…...

新能源革命风起云涌:创新科技引领可持续发展新篇章
随着全球气候变化和环境问题日益严峻,新能源革命正以其不可阻挡的势头,席卷着世界的每一个角落。 创新科技在这场革命中发挥着至关重要的作用,它不仅是新能源开发利用的引擎,更是推动可持续发展的关键力量。 新能源革命的核心在于…...

Java之TimeUnit类
1.TimeUnit类介绍 TimeUnit(时间单元)是一个描述时间单元的枚举类,在该枚举类中定义有以下的几个时间单元实例:天(DAYS)、时(HOURS)、分(MINUTES)、秒&#…...

【大数据】大数据时代的黎明
目录 前言 深入解读大数据的本质 大数据的起源与演进轨迹 大数据对社会经济的深远影响 经济领域的革新 社会治理与公共服务的智能化 创新体系的重构 面临的挑战与应对 前言 步入21世纪以来,人类文明正站在一个历史性的转折点上,迎来了大数据时代的…...

多接口分线盒在工业自动化中的重要性与应用
简介 多接口分线盒是现代工业自动化中不可或缺的一个组成部分,它主要用于简化复杂的接线系统,提高效率和可靠性。本文将详细探讨多接口分线盒的定义、功能、以及在工业自动化中的应用情况。 无源多接口分线盒 多接口分线盒的定义与功能 多接口分线盒是…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...
