1.3.数据的表示
定点数
原码
最高位是符号位,0表示正号,1表示负号,其余的n-1位表示数值的绝对值。
数值0的原码表示有两种形式:
[+0]原=0 0000000
[-0]原=1 0000000
例:1010
最高位为1表示这是一个负数,
其它三位 010 = 0*2^2 + 1*2^1 + 0*2^0 = 2
所以 等于 -2
反码
原码最大的问题就在于一个数加上它的相反数不等于0
如:0001 + 1001 = 1010
1 +(-1)= 2
正数的反码 还是等于原码
负数的反码 就是它的原码除符号位外,其它位按位取反
数值0的反码表示有两种形式:
[+0]反=0 0000000
[-0]反=1 1111111
例:1 + (-1)
原码为 0001 和 1001
取反码相加 0001 + 1111 = 1111
再将结果变回原码 1000,等于 -0
但是反码计算也不都是正确的
例如: (-1)+(-3) 用反码计算结果是 -5
因为反码只是计算的中间环节。最终由补码进行计算。
补码
正数的补码 等于它的原码
负数的补码 等于 反码+1 或 等于 (2^机器字长 - |负数|)的原码
数值0有唯一的编码:
[+0]补=0 0000000
[-0]补=0 0000000
计算机中均采用补码进行加减运算
例:若机器字长为4,计算 6 - 2
6 的补码为 0110
-2 的补码为 (2^4 - |-2|) = 14 = 1110
0110 + 1110 = 0100 = 4
移码
移码:补码的符号位取反
移码的主要用途是 表示浮点数的指数(阶码)
总结
| 正数 | 负数 | |
| 原码 | 最高位为符号位,0表示正号 其他位存放该数的二进制的绝对值 | 最高位为符号位,1表示正号 其他位存放该数的二进制的绝对值 |
| 反码 | 等于原码 | 按它的原码,除符号位外,按位取反 |
| 补码 | 等于原码 | 反码+1 或(2^机器字长 - |负数|)的原码 |
| 移码 | 补码的符号位取反 | |
浮点数
N = 尾数 * 基数^阶码(指数)
浮点数的表示格式:
| 阶符 | 阶码(移码) | 数符 | 尾数(补码) |
尾数:用补码表示,位数决定数的有效精度,位数越多精度越高
阶码:用移码表示,位数决定数的表示范围,位数越多范围越大
对阶时,小数向大数看齐
对阶是通过较小数的尾数右移实现的
相关文章:

1.3.数据的表示
定点数 原码 最高位是符号位,0表示正号,1表示负号,其余的n-1位表示数值的绝对值。 数值0的原码表示有两种形式: [0]原0 0000000 [-0]原1 0000000 例:1010 最高位为1表示这是一个负数, 其它三位 010…...

【进阶篇-Day4:使用JAVA编写石头迷阵游戏】
目录 1、绘制界面2、打乱石头方块3、移动业务4、游戏判定胜利5、统计步数6、重新游戏7、完整代码: 1、绘制界面 上述思路是:使用一个二维数组存放图片的编号,然后在后持遍历即可获取对应的图片。 代码如下: package com.itheima.s…...

探索 LLamaWorker:基于LLamaSharp的.NET本地大模型服务
LLamaWorker 是一个基于 LLamaSharp 项目开发的 HTTP API 服务器。它提供与 OpenAI 兼容的 API,使得开发者可以轻松地将大型语言模型(LLM)集成到自己的应用程序中。 1. 背景 在人工智能领域,大型语言模型(LLM…...

Qt开发 | Qt控件 | QTabWidget基本用法 | QListWidget应用详解 | QScrollArea应用详解
文章目录 一、QTabWidget基本用法二、QListWidget应用详解1.列表模式1.1 基本操作1.2 添加自定义item1.3 如何添加右键菜单1.4 QListWidget如何删除item 2.图标模式 三、QScrollArea应用详解 一、QTabWidget基本用法 QTabWidget 是 Qt 框架中的一个类,它提供了一个选…...

2023年 AI APT可持续攻击的调查研究报告
总览 随着网络技术的不断发展,网络安全威胁也日益严峻。高级持续性威胁(APT)攻击以其目标明确、手段多样、隐蔽性强等特点,成为网络安全领域的重要挑战。本文分析2023年当前 APT 攻击的主要特点、活跃组织、攻击趋势以及漏洞利用…...
Leetcode 102.目标和
给定一个正整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 ‘’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ‘’ ,在 1 之前添加 ‘-’ &…...

LLM AI工具和Delphi名称的起源
LLM AI工具和Delphi名称的起源 使用ChatGPT,直接或通过微软工具,以及其他基于llm的引擎。我很欣赏他们提供好的总结和比较的能力,并且还编写了一些样板代码。与此同时,当你问一些重要的问题时,你会得到一些令人惊讶的好…...
打破数据分析壁垒:SPSS复习必备(十一)
一、方差分析 方差分析的应用条件如下: (1)独立,各组数据相互独立,互不相关; (2)正态:即各组数据符合正态分布; (3)方差齐性&…...

【十六】【QT开发应用】Menu菜单,contextMenuEvent,setContextMenuPolicy,addAction
在 Qt 框架中,QMenu 类用于创建和管理菜单。菜单是用户界面的一部分,可以包含多个选项或动作,用户可以选择这些选项来执行特定的功能。菜单通常显示在菜单栏、上下文菜单(右键菜单)或工具栏中。 基本用法 创建菜单对象…...

华为DCN技术:M-LAG
M-LAG(Multichassis Link Aggregation Group)即跨设备链路聚合组,是一种实现跨设备链路聚合的机制。M-LAG主要应用于普通以太网络、VXLAN和IP网络的双归接入,可以起到负载分担或备份保护的作用。相较于另一种常见的可靠性接入技术…...

k8s持久化之emptyDir使用
目录 概述实践代码 概述 理解emptyDir使用,是后续k8s持久化进阶,高阶使用的基础。 实践 代码 详细说明在代码中 # 缓存数据,可以让多个容器共享数据 # 删除 Pod 时,emptyDir 数据同步消失 # 定义 initContainer -> 下载数据…...
Java露营基地预约小程序预约下单系统源码
轻松开启户外探险之旅 🌟 露营热潮来袭,你准备好了吗? 随着人们对户外生活的热爱日益增加,露营已成为许多人周末和假期的首选活动。但你是否曾因找不到合适的露营基地而烦恼?或是因为繁琐的预约流程而错失心仪的营地…...
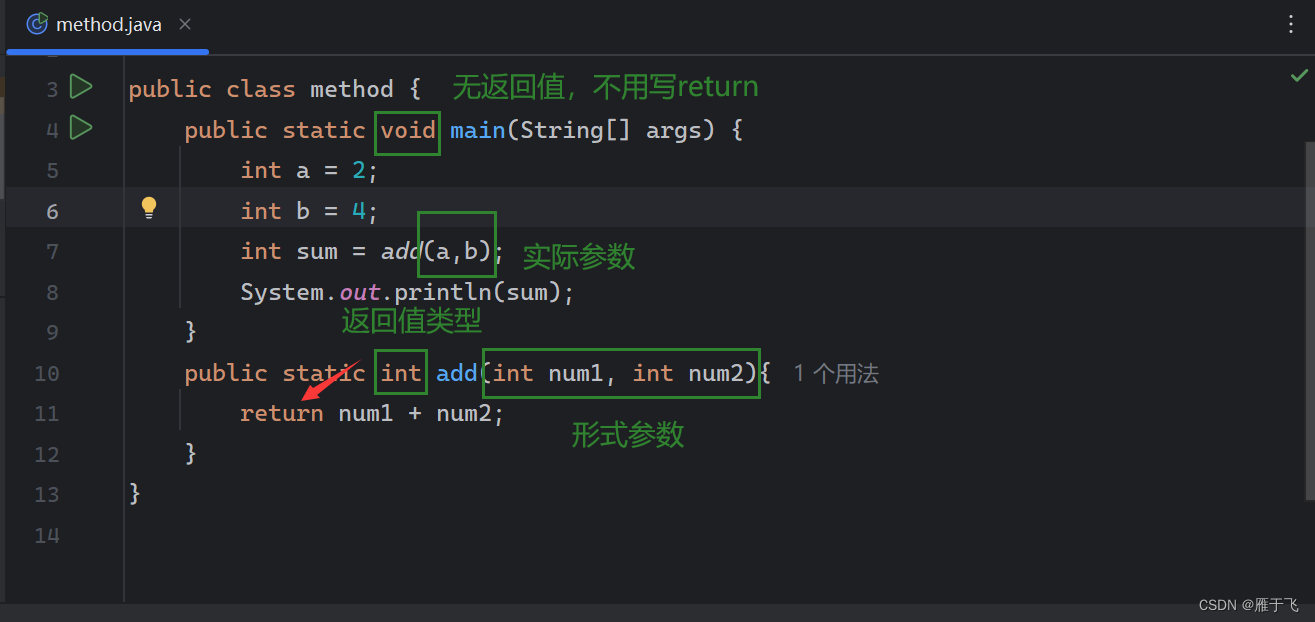
七天速通javaSE:第四天 java方法
文章目录 前言一、什么是方法?二、方法的定义与调用1. 方法的定义2. 方法的调用3. 练习:定义比大小方法并调用 三、方法的重载四、递归五、可变参数拓展:命令行传递参数 前言 本章将学习java方法。 一、什么是方法? java方法是用…...

jupyter notebook的markdown语法不起作用
在这个界面编辑,发现markdown你编辑的是什么就是什么,不起作用,然而点一下: 右上角“Notebook转发”,就会单独跳出一个jupyter notebook的界面,此时就会奏效:...
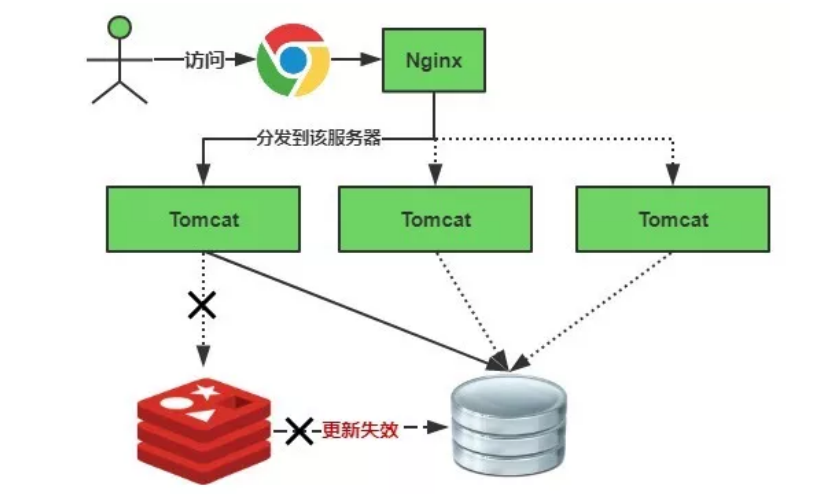
Redis 学习笔记(2)
目录 1 Redis的持久化1.1 RDB持久化方案1.2 AOF持久化方案 2 Redis架构2.1 主从复制架构2.2 哨兵集群设计2.3 哨兵集群设计 3 Redis事务机制4 Redis过期策略与内存淘汰机制4.1 过期策略4.2 内存淘汰机制 5 Redis高频面试题4.1 缓存穿透4.2 缓存击穿4.3 缓存雪崩 1 Redis的持久化…...

快慢指针:删除有序数组中的重复项
题目链接:. - 力扣(LeetCode) 思路好想,代码实现不好想 class Solution {public int removeDuplicates(int[] nums) {int fast 1,slow 1;while(fast < nums.length){if(nums[fast] ! nums[fast-1]){nums[slow] nums[fast]…...

用户登录错误次数太多锁定账号
当用户登录验证码错误次数太多时,需要限制用户在10分钟之内不能再次登录。 限制方案: 1.通过Redis ZSet key可以设置为用户名,value可以设置为UUID,score设置为当前时间戳 每次用户登录时,通过 rangeByScore 查询对…...

tedsign vue3 web-端框架中封装一个验证码组件 以及对应node 接口逻辑说明
一个这样的组件 我直接上代码了 <template><t-loading size"small" :loading"loading" show-overlay><div class"container" click"refresh"><div v-if"svg" class"svg" v-html"svg&…...

探索Scala并发编程之巅:高效并行处理的艺术
标题:探索Scala并发编程之巅:高效并行处理的艺术 引言 在现代软件开发中,随着多核处理器的普及,编写能够充分利用硬件能力的并发程序变得至关重要。Scala,这门结合了面向对象和函数式编程特性的语言,提供…...

AudioLM: 音频生成的革命性模型
AudioLM: 音频生成的革命性模型 AudioLM是一种革命性的音频生成模型,它结合了深度学习和自然语言处理的先进技术,能够生成高质量、逼真的音频内容。本文将探讨AudioLM的基本原理、工作机制、应用场景以及对音频生成领域的影响和未来发展方向。 一、Aud…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
