堆的结构与实现
堆的结构与实现
- 二叉树的顺序结构
- 堆的概念及结构
- 堆的实现
- 堆的创建
- 向上调整建堆
- 向下调整建堆
- 堆的操作链接
二叉树的顺序结构
堆其实是具有一定规则限制的完全二叉树。
普通的二叉树是不太适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树会更适合使用顺序结构进行存储。如下图:
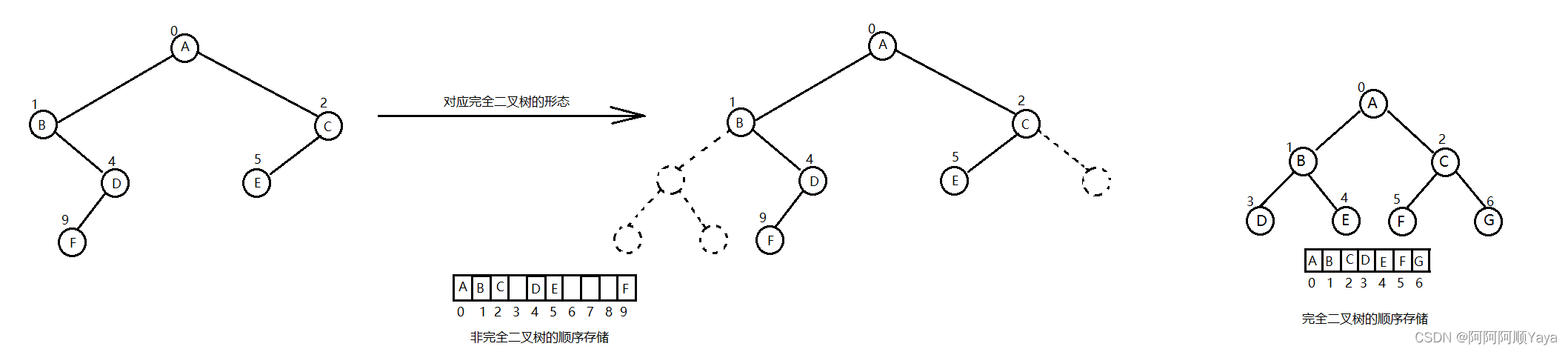
堆的概念及结构
如果有一个关键码的集合K={k0,k1,k2,...,kn−1}K=\{k_0, k_1, k_2, ..., k_{n-1}\}K={k0,k1,k2,...,kn−1},当把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并且满足:Ki≤K2∗i+1K_i\leq K_{2*i+1}Ki≤K2∗i+1且Ki≤K2∗i+2K_i\leq K_{2*i+2}Ki≤K2∗i+2(Ki≥K2∗i+1K_i\ge K_{2*i+1}Ki≥K2∗i+1且Ki≥K2∗i+2K_i\ge K_{2*i+2}Ki≥K2∗i+2),i=0, 1, 2, …,则称之为小堆(大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树。

堆的实现
堆的创建
下面给出一个数组,这个数组逻辑上可以看做一棵完全二叉树,但是还不满足堆的条件。现在我们可以通过算法,将它构建成一个堆。
int a[] = {27,15,19,18,28,34,65,49,25,37};
要将其构建成一个堆结构,有两种调整建堆的方法:一种是向上调整建堆,一种是向下调整建堆。
向上调整建堆
向上调整建堆主要是用于在堆数据结构中,堆在插入数据后,为了继续维持堆的结构,所进行的一种调整。
大致调整过程如下:
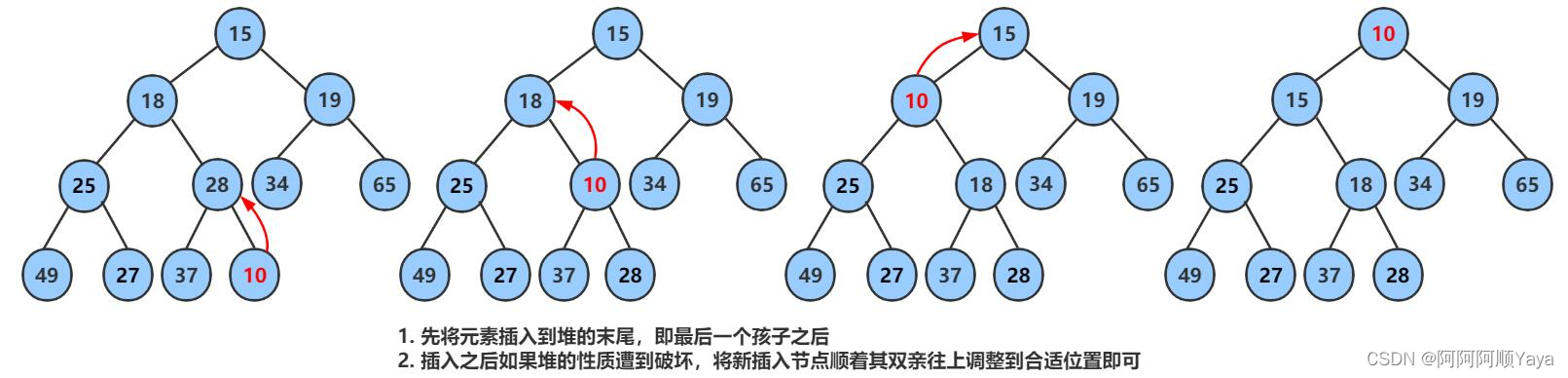
经过一次向上调整后,本来因为插入数据所导致的堆的结构的破坏就被恢复了。
有了这个思路,可以将过程实现如下:
//a - 堆的顺序存储数组
//child - 需要进行向上调整的孩子下标
void AdjustUp(HDataType* a, int child)
{assert(a != NULL);int parent = (child - 1) / 2;while (child > 0)//child为0时,child就到了堆顶,调整结束{//建小堆 - 孩子比双亲小,就互换位置if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//交换函数child = parent;parent = (child - 1) / 2;}else{break;}}
}
以上只是对一个数据进行的调整,要想实现堆的创建,需要将数组中的所有数据都进行一遍调整(堆顶元素除外),所以可以更进一步,完成一棵完全二叉树到堆的创建。
for (int i = 1; i < n; ++i)
{AdjustUp(a, i);
}
以上就是向上调整建堆的过程,我们可以分析一下它的时间复杂度。
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化,使用满二叉树来证明。(时间复杂度看的本来就是近似值,多几个节点并不影响最终结果)
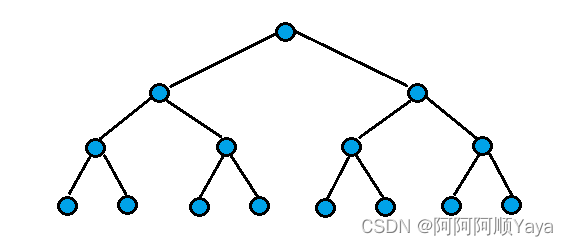
假设树的高度为h
第1层,202^020个节点,需要向上调整0层。
第2层,212^121个节点,需要向上调整1层。
第3层,222^222个节点,需要向上调整2层。
第4层,232^323个节点,需要向上调整3层。
…
第h-1层,2h−22^{h-2}2h−2个节点,需要向上调整h-2层。
第h层,2h−12^{h-1}2h−1个节点,需要向上调整h-1层。
则需要移动节点总的移动步数为:
T(n)=20∗0+21∗1+22∗2+23∗3+......+2(h−2)∗(h−2)+2(h−1)∗(h−1)T(n)=2^0*0+2^1*1+2^2*2+2^3*3+......+2^{(h-2)}*(h-2)+2^{(h-1)}*(h-1)T(n)=20∗0+21∗1+22∗2+23∗3+......+2(h−2)∗(h−2)+2(h−1)∗(h−1)
2T(n)=21∗0+22∗1+23∗2+24+3+......+2(h−1)∗(h−2)+2h∗(h−1)2T(n)=2^1*0+2^2*1+2^3*2+2^4+3+......+2^{(h-1)}*(h-2)+2^h*(h-1)2T(n)=21∗0+22∗1+23∗2+24+3+......+2(h−1)∗(h−2)+2h∗(h−1)
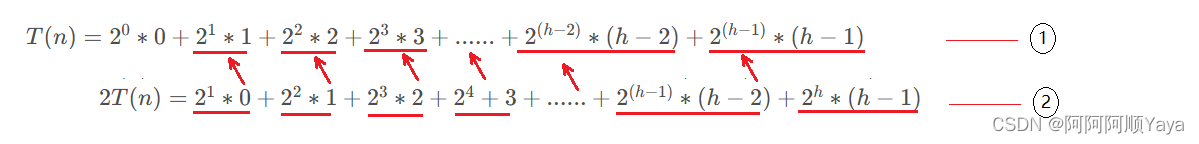
由错位相减得:
T(n)=−20−21−22−23−24−2(h−2)−2(h−1)+2h∗(h−1)T(n)=-2^0-2^1-2^2-2^3-2^4-2^{(h-2)}-2^{(h-1)}+2^h*(h-1)T(n)=−20−21−22−23−24−2(h−2)−2(h−1)+2h∗(h−1)
T(n)=2h∗(h−1)−(20+21+22+23+24+2(h−2)+2(h−1))T(n)=2^h*(h-1)-(2^0+2^1+2^2+2^3+2^4+2^{(h-2)}+2^{(h-1)})T(n)=2h∗(h−1)−(20+21+22+23+24+2(h−2)+2(h−1))
T(n)=2h∗(h−1)−(2h−1)=2h∗(h−2)+1T(n)=2^h*(h-1)-(2^h-1)=2^h*(h-2)+1T(n)=2h∗(h−1)−(2h−1)=2h∗(h−2)+1
因为是满二叉树,所以节点数n与高度h之间存在如下关系:
n=2h−1n=2^h-1n=2h−1,h=log2(n+1)h=log_2(n+1)h=log2(n+1)
所以T(n)=(n+1)∗(log2(n+1)−2)+1T(n)=(n+1)*(log_2(n+1)-2)+1T(n)=(n+1)∗(log2(n+1)−2)+1
因此,得出向上建堆的时间复杂度是O(n∗log2nn*log_2nn∗log2n)。
向下调整建堆
堆的删除
向下调整建堆主要是用于在堆数据结构中,堆在删除数据后,为了继续维持堆的结构,所进行的一种调整。
这里要说明的是,堆的删除是指删除堆顶的数据。要删除堆顶的数据并不是像顺序表那样覆盖删除。虽然堆的物理存储结构是顺序结构,但他逻辑上是树形结构,如果直接覆盖删除,本来是兄弟节点的变成父子节点,关系会完全打乱。并不能保证最终覆盖删除之后的结构还是堆的结构。
所以,堆的删除有另一种巧妙的方法。先将堆顶的数据跟堆的最后一个数据进行交换,然后删除堆的最后一个数据,就将堆顶数据删除了。
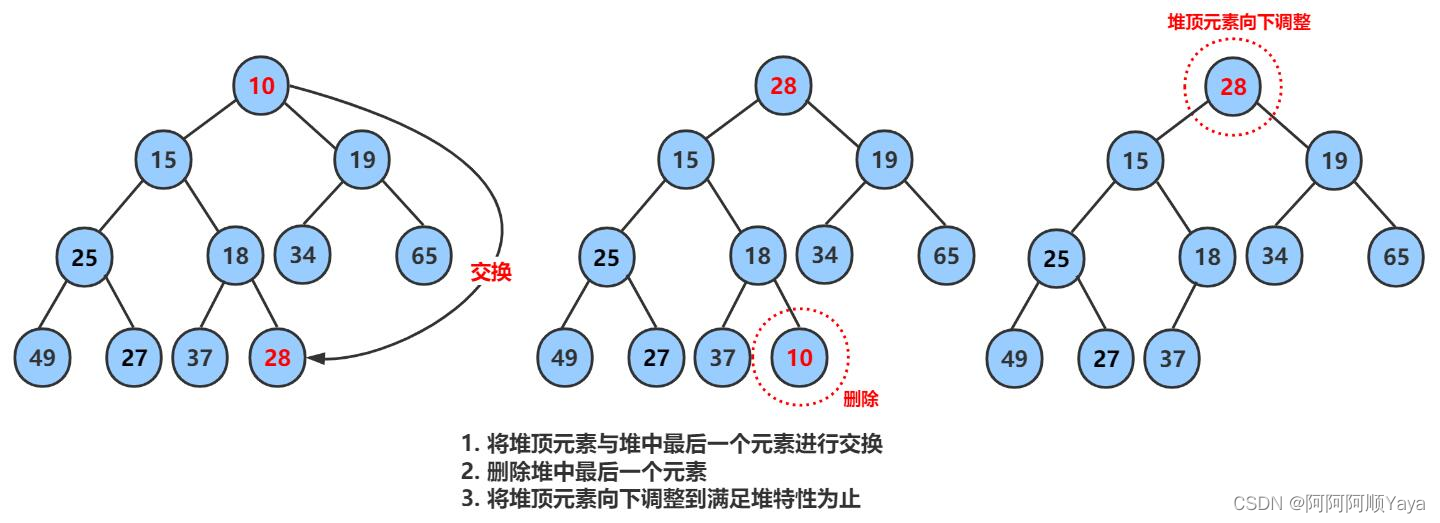
但是,堆顶的数据删除了,并没有因此就万事大吉。因为和堆顶数据进行交换的数据,现在处于堆顶位置,并不代表它就是堆中最小或最大的数据,堆的结构可能通过交换后就此被破坏。所以,这里就要通过向下调整算法来恢复堆的结构。
大致调整过程如下:
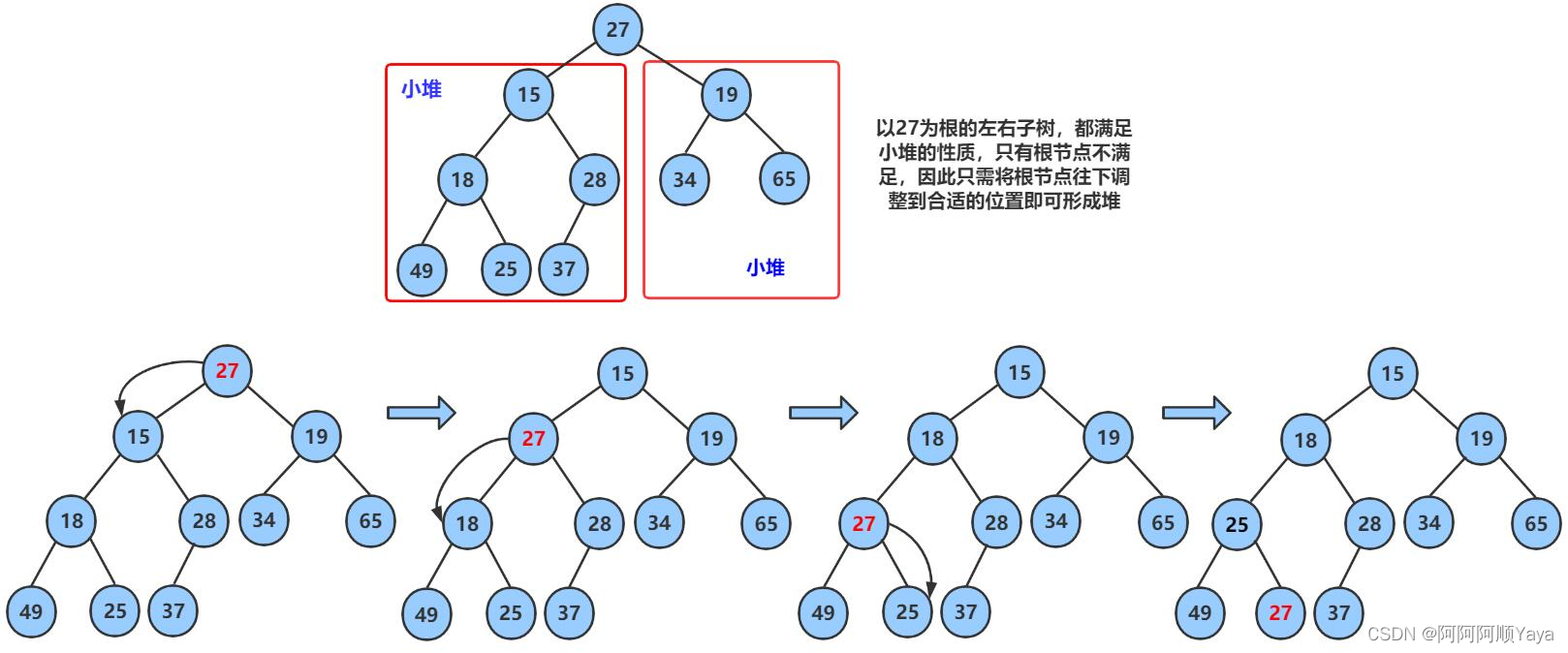
要注意的是:向下调整算法有一个前提,左右子树必须都是堆,才能调整。
经过一次向下调整后,本来因为删除数据所导致的堆的结构的破坏就被恢复了。
有了这个思路,可以将过程实现如下:
//a - 堆的顺序存储数组
//size - 堆的顺序存储数组的数据个数
//parent - 需要进行向下调整的双亲下标
void AdjustDown(HDataType* a, int size, int parent)
{assert(a != NULL);//此时child代表左孩子int child = 2 * parent + 1;//孩子下标在数组范围内进入循环while (child < size){//child+1代表右孩子//建小堆 - 右孩子存在的话,左右孩子谁更小,child存储的就是谁的下标变量if (child + 1 < size && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}
以上只是对一个数据进行的调整,要想实现堆的创建,这里我们从倒数第一个非叶子节点所形成的的子树开始调整,一直调整到根节点的树,就可以调整成堆。所以可以更进一步,完成一棵完全二叉树到堆的创建。
//n-1是最后一个数据的下标,((n-1)-1)/2是倒数第一个非叶子节点的下标
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{AdjustDown(a, n, i);
}
以上就是向下调整建堆的过程,我们可以分析一下它的时间复杂度。
同上,采取满二叉树的结构来进行复杂度的计算。
假设树的高度为h
第1层,202^020个节点,需要向下调整h-1层。
第2层,212^121个节点,需要向下调整h-2层。
第3层,222^222个节点,需要向下调整h-3层。
第4层,232^323个节点,需要向下调整h-4层。
…
第h-1层,2h−22^{h-2}2h−2个节点,需要向下调整1层。
第h层,2h−12^{h-1}2h−1个节点,需要向下调整0层。
则需要移动节点总的移动步数为:
T(n)=20∗(h−1)+21∗(h−2)+22∗(h−3)+23∗(h−4)+......+2(h−2)∗1+2(h−1)∗0T(n)=2^0*(h-1)+2^1*(h-2)+2^2*(h-3)+2^3*(h-4)+......+2^{(h-2)}*1+2^{(h-1)}*0T(n)=20∗(h−1)+21∗(h−2)+22∗(h−3)+23∗(h−4)+......+2(h−2)∗1+2(h−1)∗0
2T(n)=21∗(h−1)+22∗(h−2)+22∗(h−3)+24∗(h−4)+......+2(h−1)∗1+2h∗02T(n)=2^1*(h-1)+2^2*(h-2)+2^2*(h-3)+2^4*(h-4)+......+2^{(h-1)}*1+2^h*02T(n)=21∗(h−1)+22∗(h−2)+22∗(h−3)+24∗(h−4)+......+2(h−1)∗1+2h∗0
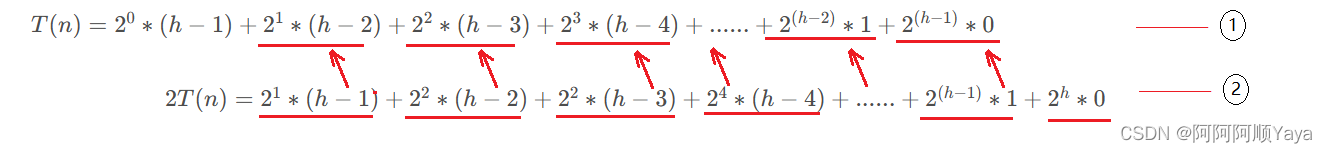
由错位相减得:
T(n)=(1−h)+21+22+23+24+2(h−2)+2(h−1)T(n)=(1-h)+2^1+2^2+2^3+2^4+2^{(h-2)}+2^{(h-1)}T(n)=(1−h)+21+22+23+24+2(h−2)+2(h−1)
T(n)=20+21+22+23+24+2(h−2)+2(h−1)−hT(n)=2^0+2^1+2^2+2^3+2^4+2^{(h-2)}+2^{(h-1)}-hT(n)=20+21+22+23+24+2(h−2)+2(h−1)−h
T(n)=2h−1−hT(n)=2^h-1-hT(n)=2h−1−h
因为是满二叉树,所以节点数n与高度h之间存在如下关系:
n=2h−1n=2^h-1n=2h−1,h=log2(n+1)h=log_2(n+1)h=log2(n+1)
所以T(n)=n−long2(n+1)T(n)=n-long_2(n+1)T(n)=n−long2(n+1)
因此,得出向下建堆的时间复杂度是O(n)。
通过比较,向上建堆的时间复杂度是O(n∗log2nn*log_2nn∗log2n),向下建堆的时间复杂度是O(n),所以采取向下建堆会更优一些。
以上过程都是对小堆的建立,如果要建大堆,只需要将判断条件略作更改即可:
//建小堆
if (a[child] < a[parent])
if (child + 1 < size && a[child + 1] < a[child])
if (a[child] < a[parent])//建大堆:
if (a[child] > a[parent])
if (child + 1 < size && a[child + 1] > a[child])
if (a[child] > a[parent])
堆的操作链接
最后,对于堆的各种操作需求,可以参考阿顺的这篇堆(C语言实现)
相关文章:
堆的结构与实现
堆的结构与实现二叉树的顺序结构堆的概念及结构堆的实现堆的创建向上调整建堆向下调整建堆堆的操作链接二叉树的顺序结构 堆其实是具有一定规则限制的完全二叉树。 普通的二叉树是不太适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树会更适合使用顺…...

Pandas快速入门
Pandas是Python中非常流行的数据处理库之一,它提供了一种简单而强大的方法来处理和分析数据。在本篇文章中,我将向你介绍Pandas的基础知识,以便你可以开始使用它来处理和分析数据。 安装Pandas 首先,你需要安装Pandas。可以通过…...
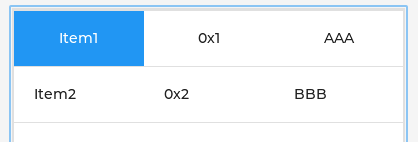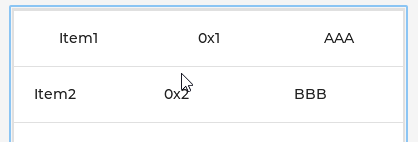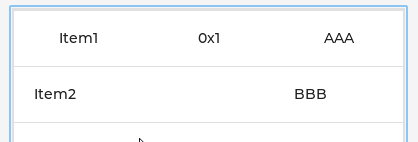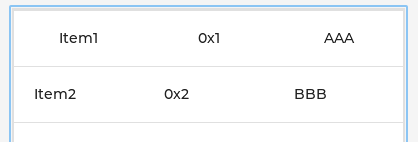
LVGL学习笔记18 - 表Table
目录 1. Parts 1.1 LV_PART_MAIN 1.2 LV_PART_ITEMS 2. 样式 2.1 设置行列数 2.2 设置单元格字符串 2.3 设置单元格宽度 2.4 设置表格高度和宽度 2.5 设置字符串颜色 2.6 设置边框颜色 2.7 设置背景颜色 3. 事件 4. CELL CTRL 表格是由包含文本的行、列和单元格构…...

嵌入式安防监控项目——html框架分析和环境信息刷新到网页
目录 一、html控制LED 二、模拟数据上传到html 一、html控制LED 简单来说就是html给boa服务器发了一个控制指令信息,然后boa转发给cgi进程,cgi通过消息队列和主进程通信。主进程再去启动LED子线程。 这是老师给的工程。 以前学32都有这工具那工具来管…...
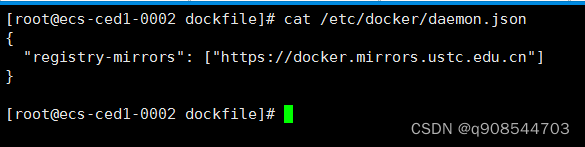
centos安装docker详细步骤
目录 一.前言 1.环境要求2.官网中文安装参考手册 二.安装步骤 1.卸载旧版本2.安装需要的软件包3.设置docker镜像源 1.配置docker镜像源 方式1:官网地址(外国):方式2:阿里云源:2.查看配置是否成功 4.更新yum软件包索引5.可以查看…...
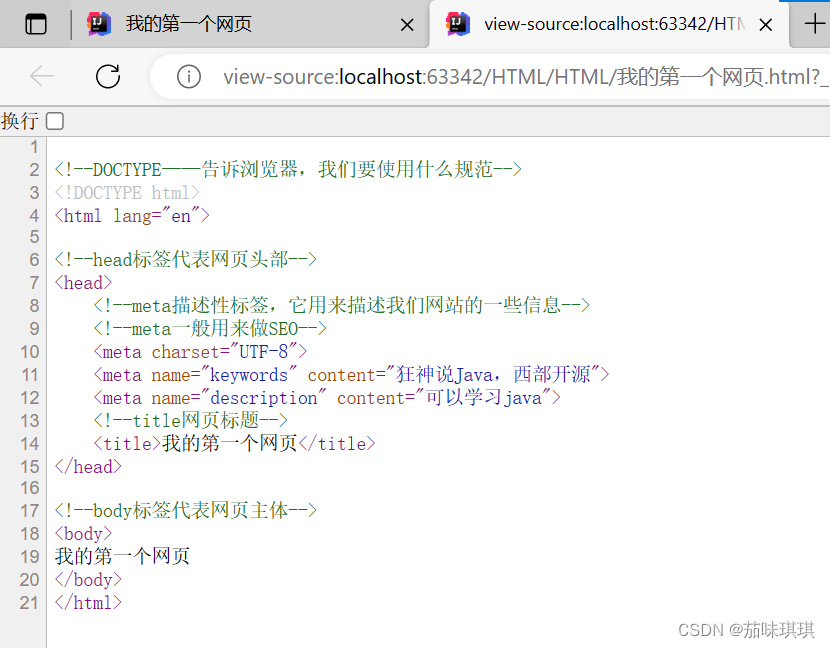
初识HTML、W3C标准、如何利用IDEA创建HTML项目、HTML基本结构、网页基本信息
一、什么是HTML? HTML——Hyper Text Markup Languagr(超文本标记语言) 超文本包括:文字、图片、音频、视频、动画等 目前网页中常用——HTML5 HTML5提供了一些新的元素和一些有趣的新特性,同时也建立了一些新的规则…...

为什么程序员喜欢这些键盘?
文章目录程序员的爱介绍个人体验程序员的爱 程序员是长时间使用计算机的群体,他们需要一款高品质的键盘来保证舒适的打字体验和提高工作效率。在键盘市场上,有很多不同类型的键盘,但是对于程序员来说,机械键盘是他们最钟爱的选择…...

JS中数组去重的几种方法
JS 中有多种方法可以实现数组去重,下面是几种常用的方法:1、使用 Set 去重:Set 数据结构中不能有重复元素,可以将数组转成 Set 类型,再转回数组。let arr [1,2,3,4,5,6,2,3,4]; let uniqueArr [...new Set(arr)]; co…...

Nginx 配置实例-负载均衡
一、实现效果 浏览器地址栏输入地址 http://192.168.137.129/edu/a.html,负载均衡效果,将请求平均分配到8080和8081两台服务器上。 二、准备工作 1. 准备两台tomcat服务器,一台8080,一台8081 (具体操作如下两个链接) Nginx配置实…...

引出生命周期、生命周期_挂载流程、生命周期_更新流程、生命周期_销毁流程、生命周期_总结——Vue
目录 一、引出生命周期 二、生命周期_挂载流程 三、生命周期_更新流程 四、生命周期_销毁流程 五、生命周期_总结 一、引出生命周期 生命周期: 1.又名:生命周期回调函数、生命周期函数、生命周期钩子。 2.是什么:Vue在关键时刻帮我们调…...

C++ STL学习之【vector的使用】
✨个人主页: Yohifo 🎉所属专栏: C修行之路 🎊每篇一句: 图片来源 The power of imagination makes us infinite. 想象力的力量使我们无限。 文章目录📘前言📘正文1、默认成员函数1.1、默认构造…...

方差分析与单因素方差分析
研究分类型自变量对数值型因变量的影响。检验统计的设定和检验方法与变量间的方差是否相等有关。 例如研究行业、服务等级对投诉数的影响:如表格中给出4个行业、每个行业有3个服务等级、样本容量为7、观测值为投诉数。则构成一个3维的矩阵。 在上述基础上…...

分布式链路追踪组件skywalking介绍
SkyWalking组件概念 一个开源的可观测平台, 用于从服务和云原生基础设施收集, 分析, 聚合及可视化数据。SkyWalking 提供了一种简便的方式来清晰地观测分布式系统, 甚至横跨多个云平台。SkyWalking 更是一个现代化的应用程序性能监控(Application Performance Monitoring)系统…...
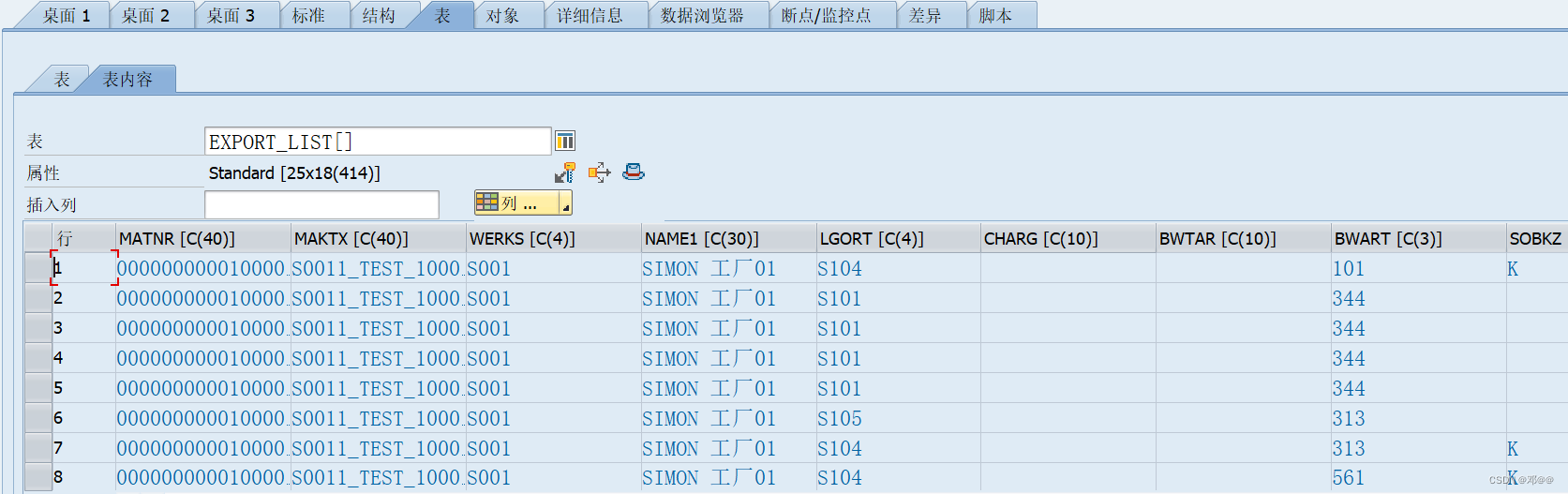
SUBMIT的用法
SUBMIT的用法 一、简介 系统MB52/MB51/MB5B等类似的报表 ,虽然数据很全面,执行效率也够快,但是经常会不满足用户需求(增添字段、添加查询条件等),很多ABAP 会选择去COPY出标准程序,然后去做修改…...

网页基本标签、图像标签、链接标签、块内元素和块元素、列表标签、表格标签
一、网页基本标签 标题标签 段落标签 未写段落标签前,文本没有按照想要的格式排列显示 写段落标签后: 每句都是一段,所以句与句距离比较宽 换行标签 同一段,只是把文字换行,所以比较紧凑 水平线标签 字体样式标签 …...
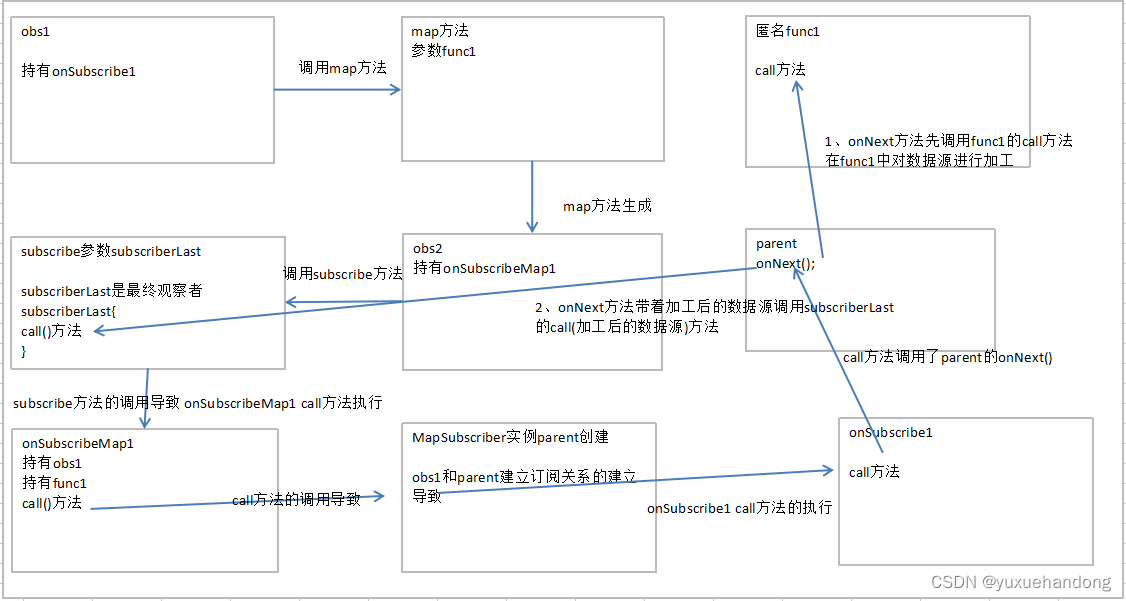
RxJava操作符变换过程
要使用Rxjava首先要导入两个包,其中rxandroid是rxjava在android中的扩展 implementation io.reactivex:rxandroid:1.2.1implementation io.reactivex:rxjava:1.2.0我们在使用rxjava的操作符时都觉得很方便,但是rxjava是怎么实现操作符的转换呢࿰…...

开放平台订单接口
custom-自定义API操作 注册开通 taobao.custom 公共参数 名称 类型 必须 描述 key String 是 调用key(必须以GET方式拼接在URL中) secret String 是 调用密钥 api_name String 是 API接口名称(包括在请求地址中&a…...

CDN相关知识点
1、什么是CDN?CDN的作用是什么? CDN(Content Delivery Network,内容分发网络)是一种通过在多个节点上分布内容以提高网络性能、可靠性和可扩展性的网络解决方案。CDN通过在不同的地理位置部署服务器,使用户…...
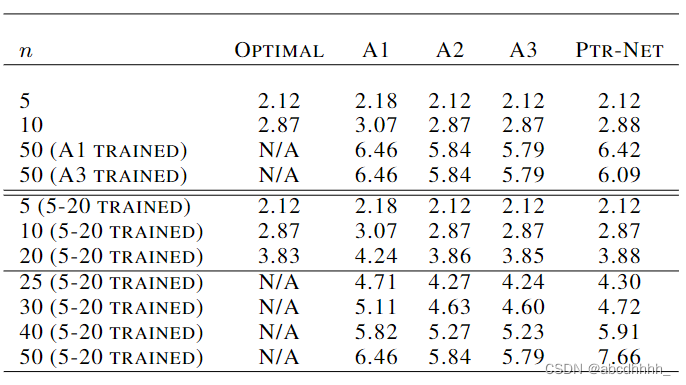
【论文阅读】注意力机制与二维 TSP 问题
前置知识 注意力机制 见 这篇 二维 TSP 问题 给定二维平面上 nnn 个点的坐标 S{xi}i1nS\{x_i\}_{i1}^nS{xi}i1n,其中 xi∈[0,1]2x_i\in [0,1]^2xi∈[0,1]2,要找到一个 1∼n1\sim n1∼n 的排列 π\piπ ,使得目标函数 L(π∣s)∥xπ…...
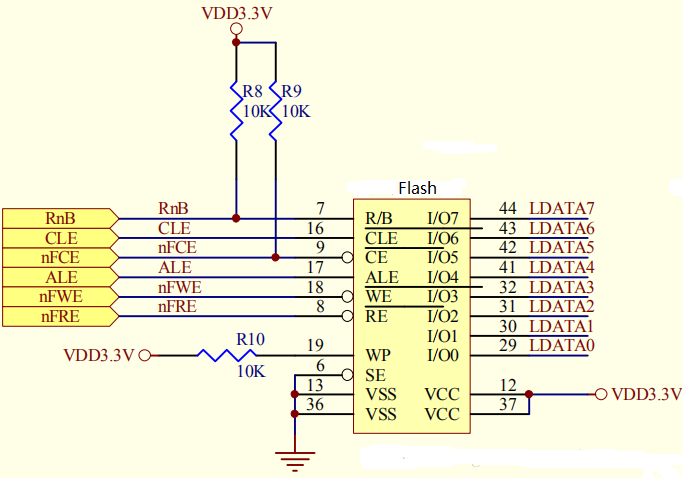
[深入理解SSD系列 闪存实战2.1.7] NAND FLASH基本编程(写)操作及原理_NAND FLASH Program Operation 源码实现
前言 上面是我使用的NAND FLASH的硬件原理图,面对这些引脚,很难明白他们是什么含义, 下面先来个热身: 问1. 原理图上NAND FLASH只有数据线,怎么传输地址? 答1.在DATA0~DATA7上既传输数据,又传输地址 当ALE为高电平时传输的是地址, 问2. 从N...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
