当前位置： 首页 > news >正文

汕头网站搭建/b站黄页推广

news 文章来源：https://blog.csdn.net/weixin_42907150/article/details/129469590 2025/2/28 3:06:19
汕头网站搭建,b站黄页推广,国内正品购物app排行,萍乡今日头条新闻因果图&判定表法 在了解了等价类和边界值比较适宜搭档的测试用例方法之后 接下来我们来了解另外一队就是因果图和判定表 因果图会产生判定表法 因果图法 等价类划分法和边界值分析方法都是着重考虑输入条件而不考虑输入条件的各种组合、输入条件之间的相互制约关系。例…

因果图&判定表法

在了解了等价类和边界值比较适宜搭档的测试用例方法之后

接下来我们来了解另外一队就是因果图和判定表

因果图会产生判定表法

因果图法

  • 等价类划分法和边界值分析方法都是着重考虑输入条件
  • 而不考虑输入条件的各种组合、输入条件之间的相互制约关系。例如地区的选择
  • 如果在测试时必须考虑输入条件的各种组合，则可能的组合数目将是天文数字
  • 因此必须考虑采用一种适合于描述多种条件的组合、产生多个相应动作的测试方法，这就需要利用因果图（逻辑模型）

因果图-判定表

  • 因果图法基于这样的思想：一些程序的功能可以用决策表的形式来表示，并根据输入条件的组合情况规定相应的操作
  • 因此，可以考虑为决策表中的每一列设计一个测试用例，以便测试程序在输入条件的某种组合下的输出是否正确
  • 概括的说，因果图法就是从程序规格说明书的描述中找出因（输入条件）和果（输出结果或程序状态的改变）
  • 将因果图转换为判定表，为判定表（也叫做决策表）中的每一列设计一个测试用例
  • 这种方法考虑到了输入情况的各种组合以及各个输入情况之间的相互制约关系（那些有互斥，那些无互斥这种情况）

判定表

  • 判定表(decision table)是分析和表达多逻辑条件下执行不同操作的工具
  • 在程序设计发展的初期，判定表就已被当做编写程序的辅助工具
  • 因为他可以把复杂的逻辑关系和多种条件组合的情况表达得具体

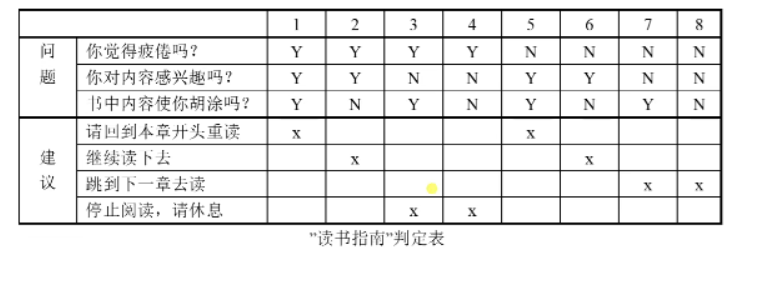
image-20230311203914711

  • 判定表通常由四个部分组成
    • 条件桩：列出了问题的所有条件，通常认为列出的条件的次序无关紧要。类似于你感到疲惫吗？你对内容感兴趣吗？
    • 动作桩：列出了问题规定可能采取的操作，这些操作的排列顺序没有约束，这些结果一般都是互相排斥的。例如请回到本章开头重读，继续读下去
    • 条件项：列出针对他左列条件的取值，在所有可能情况下的真假值
    • 动作项：列出在条件项的各种取值情况下应该采取的动作

设计步骤

  1. 分析软件规格说明中那些是原因（即输入条件或输入条件的等价类），那些是结果（即输出条件），并给予每个原因和结果赋予一个标识符
  2. 分析软件规格说明中语义的内容，找出原因与结果之间、原因与原因之间对应的关系，根据这些关系画出因果图。==直接画出判定表
  3. 由于语法或环境的限制，有些原因与原因之间、原因与结果之间的组合情况不可能出现。为表明这些特定的情况，在因果图上使用一些记号表明约束或限制条件
  4. 把因果图转换为判定表
  5. 根据判定表中的每一列设计测试用例

注意，虽然这些都是约定速成的，但是我们可以进行简化

实战

  • 使用因果图+判定表设计测试用例测试两位数加法计算器
image-20230311213125475

当然，这个例子可能不是那么那么标准。但是不要紧，后面还用一些例子进行补充，

  • 输入1：
    • 条件1：0<=x<=99
    • 条件2: -99<=x<0
    • 条件3: x<-99
    • 条件4: x>99
  • 输入2：
    • 条件1：0<=x<=99
    • 条件2: -99<=x<0
    • 条件3: x<-99
    • 条件4: x>99
  • 输出
    • 正确计算
    • 错误提示

分析条件互斥

  • 输入
    • 输入1：
      • 1 2 3 4 互斥
    • 输入2：
      • 1 2 3 4 互斥
  • 输出
    • 输出结果正确和错误互斥

跳过因果图

分析、简化并画出判定表

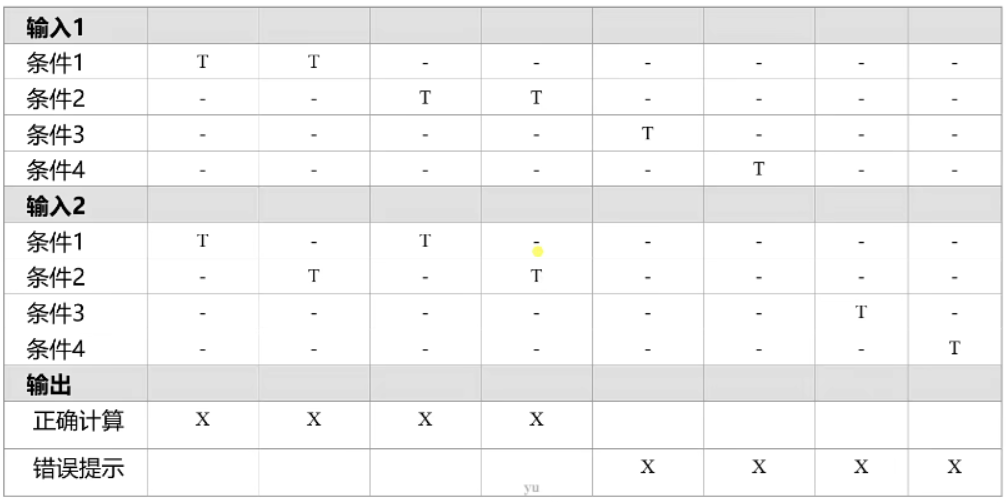
image-20230311213721327

这里的“-”是具有普适性的。也就是说当条件3成立，输入2里不管什么值该输出结果都是错误提示。

条件1 2 是有效等价类， 条件 3 4 是无效等价类

有效等价类会产生4种结果，无效的也是4种结果

以列为单位，写出测试用例。比如第一列，可能取值为90 + 90 = 180

以此类推，取出8层测试用例额

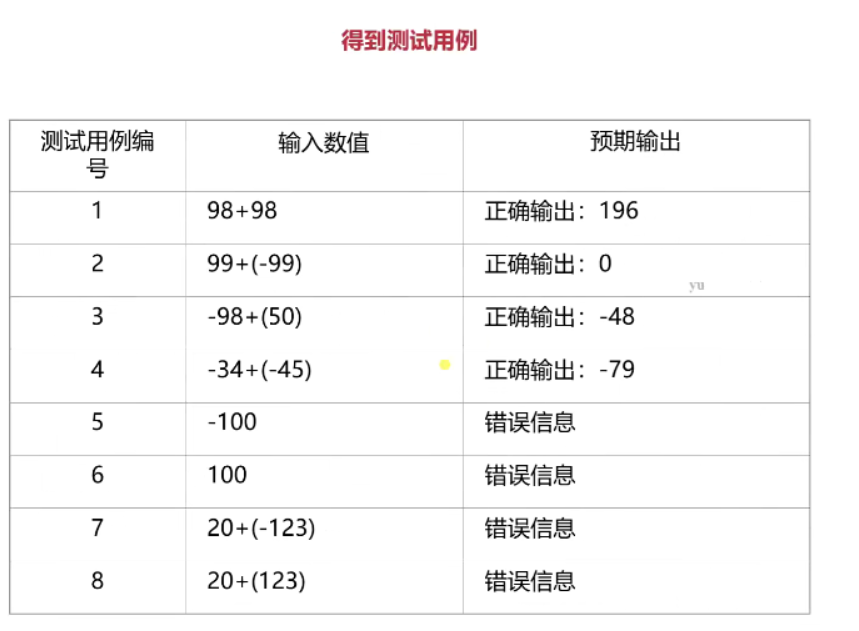
image-20230311214023222

因果图法用例设计联系

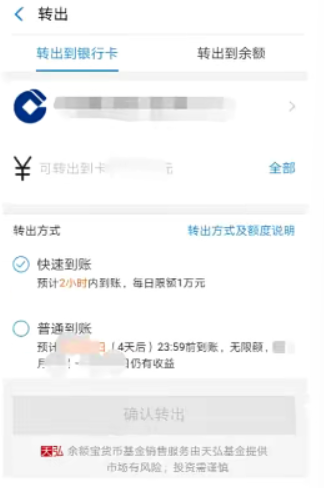
image-20230311214239194
  • 同理我们将同一测试需求用因果图设计
  • 余额宝提现到银行卡增加新规则：快速到账（2小时）日限额1w元，超过1w元只能选择普通到账
  • 按照y因果图法设计测试用例

分析输入条件和输出条件

  • 输入
    • 输入1：
      • a1：快速体现
      • a2：普通体现
    • 输入2：
      • a1：0<x<=10000
      • a2: x<=0
      • a3: x>10000
  • 输出
    • b1：提现成功
    • b2：提现失败

分析、简化并画出判定表

image-20230311214555073

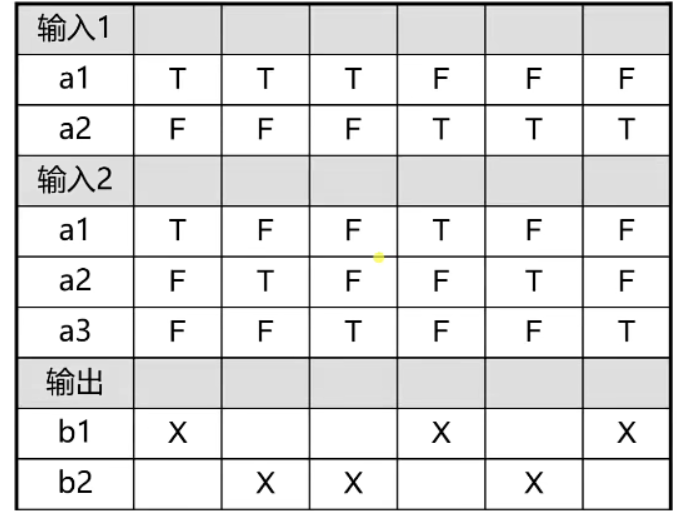
这三类条件都是互斥的

经典因果图-判定表面试题

  • 问题：某厂工资发放
  • 描述、分析：
    • 工资分为年薪制a1，月薪制a2
    • 错误程度分为普通a3，严重a4
    • 工资为a1的员工犯普通错误扣工资2%(b1)，犯严重错误扣工资6%（b2）
    • 工资为a2的员工犯普通错误的扣工资4%(b3),犯严重错误扣工资8%(b4)
    • 其中a1和a2为互斥，b1 b2和 b3 b4是互斥，a3 a4可以同时具备
输入
a1TTTTFFFF
a2FFFFTTTT
a3TFTFTFTF
a4FTTFFTTF
输出
b1××
b2××
b3××
b4××

相关文章：

因果图判定表法

因果图&判定表法 在了解了等价类和边界值比较适宜搭档的测试用例方法之后 接下来我们来了解另外一队就是因果图和判定表 因果图会产生判定表法 因果图法 等价类划分法和边界值分析方法都是着重考虑输入条件而不考虑输入条件的各种组合、输入条件之间的相互制约关系。例…...

编程日记 2023/3/12 2:20:28

Oracle 数据库相关信息清单列表

Oracle 数据库相关信息清单列表 一、设置Oracle安装目录 Oracle基目录（ORACLE_BASE）：D:\databases\oracle\oracle_11g\app\Administrator 软件位置（ORACLE_HOME）：D:\databases\oracle\oracle_11g\app\Administrator\product\11.2.0\dbhome_1 数据库文件位置：D:\databa…...

编程日记 2023/3/12 2:19:23

射频资料搜集--推荐几个网站和链接

https://picture.iczhiku.com/resource/eetop/wHKYFQlDTRRShCcc.pdfhttps://picture.iczhiku.com/resource/eetop/wHKYFQlDTRRShCcc.pdfVCO pulling的资料 模拟滤波器与电路设计手册 - 射频微波仿真 - RF技术社区 Practical RF Amplifier Design Using the Available Gain Pr…...

编程日记 2023/3/12 2:18:17

B1048 数字加密

decription 本题要求实现一种数字加密方法。首先固定一个加密用正整数 A&#xff0c;对任一正整数 B&#xff0c;将其每 1 位数字与 A 的对应位置上的数字进行以下运算&#xff1a;对奇数位&#xff0c;对应位的数字相加后对 13 取余——这里用 J 代表 10、Q 代表 11、K 代表 …...

编程日记 2023/3/12 2:17:12

Qt使用FFmpeg播放视频

一、使用场景 因为项目中需要加载MP4播放开机视频&#xff0c;而我们的设备所使用的架构为arm架构&#xff0c;其中缺乏一些多媒体库。安装这些插件库比较麻烦&#xff0c;所以最终决定使用FFmpeg播放视频。 二、下载编译ffmpeg库 2.1 下载源码 源码下载路径&#xff1a;http…...

编程日记 2023/3/12 2:16:11

Win32 ListBox控件

Win32 ListBox控件 创建ListBox控件 创建窗口函数 HWND CrateWindowEx(DWORD dwExStyle , // 窗口的扩展风格,基本没用LPCTSTR lpClassName, // 已经注册的窗口类名称LPCTSTR lpWindowName, // 窗口标题栏的名字DWORD dwStyle, // 窗口的基本风格int x, // 左上角水平坐标int …...

编程日记 2023/3/12 2:15:08

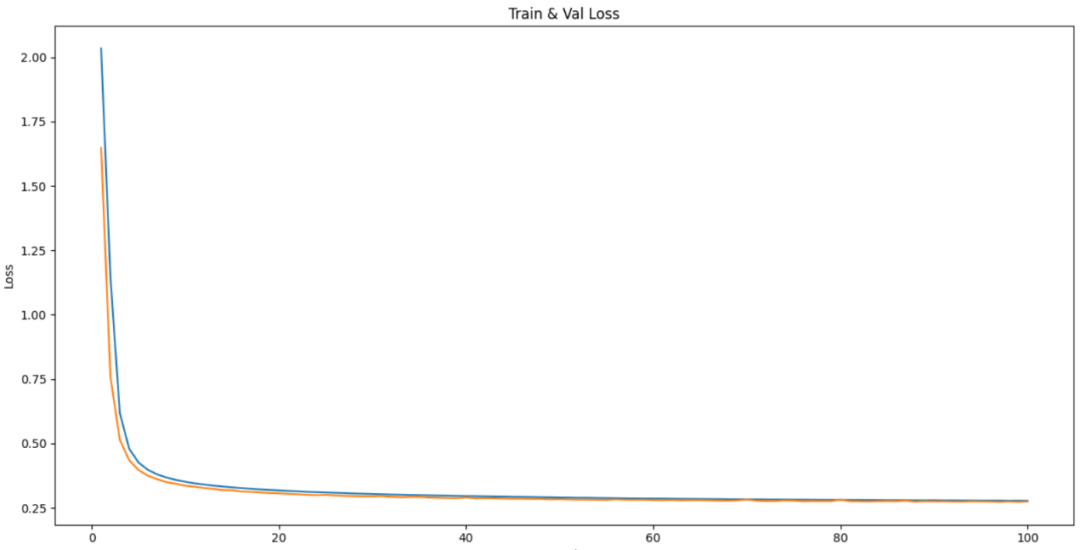
最大值池化与均值池化比较分析

1 问题在深度学习的卷积网络过程中&#xff0c;神经网络有卷积层&#xff0c;池化层&#xff0c;全连接层。而池化层有最大值池化和均值池化两种情况&#xff0c;而我们组就在思考&#xff0c;最大值池化和均值池化有什么区别呢&#xff1f;两者的模型准确率是否有所不同&#…...

编程日记 2023/3/12 2:14:05

统计学 多元线性回归

文章目录统计学 多元线性回归多元线性回归模型拟合优度显著性检验线性关系检验回归系数检验多重共线性及其处理多重共线性的问题多重共线性的识别与处理变量选择利用回归方程进行预测哑变量回归统计学 多元线性回归 多元线性回归模型 多元线性回归模型&#xff1a;设因变量为…...

编程日记 2023/3/12 2:13:02

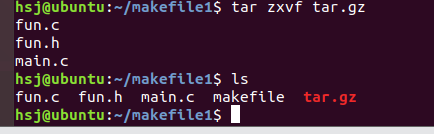
tar和gzip压缩和解压

打包和压缩的区别&#xff1a;打包&#xff1a;将多文件 封装在一起压缩&#xff1a;将多文件 封装在一起 通过特定的算法 将冗余的数据 进行删除tar默认是打包命令&#xff0c;如果想用tar进行压缩 必须加选项1、gzip格式压缩&#xff1a;tar zcvf 压缩包包名 文件1 文件2 文件…...

编程日记 2023/3/12 2:11:58

搭建Docker企业私有仓库

什么是仓库 仓库&#xff08;Repository&#xff09;是存储和分发 Docker 镜像的地方。镜像仓库类似于代码仓库&#xff0c;Docker Hub 的命名来自 GitHub&#xff0c;Github 是我们常用的代码存储和分发的地方。同样 Docker Hub 是用来提供 Docker 镜像存储和分发的地方。 谈…...

编程日记 2023/3/12 2:10:52

[NOIP2009 提高组] 最优贸易（C++，tarjan，topo，DP）

题目描述 $C 国有国有国有 n 个大城市和个大城市和个大城市和 m$ 条道路&#xff0c;每条道路连接这 nnn个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 mmm 条道路中有一部分为单向通行的道路&#xff0c;一部分为双向通行的道路&#xff0c;双向通行的…...

编程日记 2023/3/12 2:09:47

计算机网络：移动IP

移动IP相关概念 移动IP技术是移动结点&#xff08;计算机/服务器&#xff09;以固体的网络IP地址&#xff0c;实现跨越不同网段的漫游功能&#xff0c;并保证了基于网络IP的网络权限在漫游中不发生任何改变。移动结点&#xff1a;具有永久IP地址的设备。归属代理&#xff08;本…...

编程日记 2023/3/12 2:08:45

binutils工具集——GNU binutils工具集简介

以下内容源于网络资源的学习与整理&#xff0c;如有侵权请告知删除。 GNU binutils是一个二进制工具集&#xff0c;主要包括&#xff1a; ld&#xff0c;GNU链接器。as&#xff0c;GNU汇编器。addr2line&#xff0c;把地址转化为文件名和行号。nm&#xff0c;列出目标文件的符…...

编程日记 2023/3/12 2:07:42

Golang编译选项(ldflags)有趣应用

本文介绍如何在构建时使用ldflags选项给Golang应用程序注入变量&#xff0c;用于给Go可执行文件增加版本标识或GIT提交摘要等信息。 应用程序的版本信息 我们首先查看Docker Cli 包含的提交信息&#xff1a; docker version 返回结果&#xff1a; Server: Docker Engine - Co…...

编程日记 2023/3/12 2:06:40

AIR32F103(十一) 在AIR32F103上移植微雪墨水屏驱动

目录 AIR32F103(一) 合宙AIR32F103CBT6开发板上手报告AIR32F103(二) Linux环境和LibOpenCM3项目模板AIR32F103(三) Linux环境基于标准外设库的项目模板AIR32F103(四) 27倍频216MHz,CoreMark跑分测试AIR32F103(五) FreeRTOSv202112核心库的集成和示例代码AIR32F103(六) ADC,I2S…...

编程日记 2023/3/12 2:05:37

Uipath Excel 自动化基础系列文章

Uipath Excel 自动化基础系列文章已发布到CSDN,网址&#xff1a;https://blog.csdn.net/Marshaljun?typeblog (3月份会在CSDN博客发布Uipath Excel 实战课程及经验分享) Uipath Studio流程设计器介绍 https://blog.csdn.net/Marshaljun/article/details/128699022 Uipath St…...

编程日记 2023/3/12 2:04:35

神经网络优化器之随机梯度下降法的理解

随机梯度下降法&#xff08;SGD&#xff09;随机梯度下降方法&#xff0c;在每次更新时用1个样本&#xff0c;随机也就是说我们用样本中的一个例子来近似我所有的样本&#xff0c;由于计算得到的并不是准确的一个梯度&#xff0c;因而不是全局最优的。但是相比于批量梯度&#…...

编程日记 2023/3/12 2:03:33

记录一次WIN11开机在登录页面循环的问题

记录一次由于未进行win密码设置&#xff0c;导致开机后卡在登录界面无法登录进去的问题。最后完美解决了。 1. 背景 开机后&#xff0c;显示用户登录界面&#xff0c;但是和以往不同&#xff0c;没有了密码输入框&#xff0c;只有一个“登录”按钮孤零零地显示在屏幕中间&…...

编程日记 2023/3/12 2:02:30

始终从最不易改变的方面开始

在你刚开始新工作、转换职业或者是加入新项目时&#xff0c;始终从最不易改变的方面开始。 在工作中&#xff0c;这可能意味着与团队成员建立关系&#xff0c;了解公司的流程和文化&#xff0c;或者熟悉公司的产品或服务。 在一项新项目中&#xff0c;这可能意味着了解项目范…...

编程日记 2023/3/12 2:01:28

4、Httpclient源码解析之HTTP协议

初始化CloseableHttpClient过程中涉及ExecChainHandler & DefaultHttpProcessor&#xff0c;即典型客户端责任链中的请求执行处理器。 责任链中各节点涉及请求处理器【ExecChainHandler】顺序如下&#xff1a;RedirectExec、ContentCompressionExec、HttpRequestRetryExec…...

编程日记 2023/3/12 2:00:26

浏览器并发行为记录

使用nodejs koa起一个服务&#xff0c;使请求延时返回。 服务端代码 /** 延时 */ exports.timeoutTestData async function (ctx) {console.log(get query:, ctx.request.query);const query ctx.request.query;let timeout query.timeout || 2000;await new Promise(res…...

编程日记 2023/3/12 1:59:22

工厂模式与抽象工厂

原理&#xff1a;逻辑和业务全部封装 不需要细节 只要结果 示例&#xff1a; # 简单工厂 class SimpleFactory:# 产品staticmethoddef product(name):return nameif __name__ "__main__":product SimpleFactory.product("Gitee")print(product) 装饰器…...

编程日记 2023/3/12 1:58:19

什么？你不知道 ConcurrentHashMap 的 kv 不能为 null?

一、背景 最近设计某个类库时使用了 ConcurrentHashMap 最后遇到了 value 为 null 时报了空指针异常的坑。 本文想探讨下以下几个问题&#xff1a; &#xff08;1&#xff09; Map接口的常见子类的 kv 对 null 的支持情况。 &#xff08;2&#xff09;为什么 ConcurrentHashM…...

编程日记 2023/3/12 1:57:18

SQL复习04 | 复杂查询

1. 视图 视图和表的区别&#xff1a; 表保存的是实际的数据视图保存的是SELECT语句 视图的优点&#xff1a; 视图无需保存数据&#xff0c;可节省存储设备的容量可以将频繁使用的SELECT语句保存成视图&#xff0c;可大大提高效率 1.1 创建视图 CREATE VIEW 视图名称&…...

编程日记 2023/3/12 1:56:16

【面试题】Java面试题汇总(无解答)

此内容会持续补充。。。 基础 short s1 1; s1 s1 1;有错吗? short s1 1; s1 1; 有错吗&#xff1f;String str”aaa”,与 String strnew String(“aaa”)一样吗&#xff1f;String 和 StringBuilder、StringBuffer 的区别&#xff1f;Sring最大能存多大内容&#xff1f…...

编程日记 2023/3/12 1:55:14

C++---背包模型---收服精灵（每日一道算法2023.3.11）

注意事项&#xff1a; 本题是"动态规划—01背包"的扩展题&#xff0c;优化的思路不多赘述&#xff0c;dp思路会稍有不同&#xff0c;下面详细讲解。 本题偏向阅读理解&#xff0c;给每种变量归类起名字很有帮助哦。 切记先看思路&#xff0c;再看代码。&#xff08;大…...

编程日记 2023/3/12 1:54:10

day30_JS

今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、作业 二、BOM 三、定时器 四、正则表达式 零、 复习昨日 事件 事件绑定方式鼠标事件 onmouseoveronmouseoutonmousemove 键盘事件 onkeydownonkeyupon…...

编程日记 2023/3/12 1:53:08

【Java学习笔记】19.Java 正则表达式(2)

前言 本章继续介绍Java的正则表达式。 Matcher 类的方法 索引方法 索引方法提供了有用的索引值&#xff0c;精确表明输入字符串中在哪能找到匹配&#xff1a; 序号方法及说明1public int start()返回以前匹配的初始索引。2public int start(int group)返回在以前的匹配操作…...

编程日记 2023/3/12 1:51:00

华为云arm架构轻松安装kubeedge

先安装k8s 华为云arm架构安装k8s(kubernetes) 下载kubeedge需要的软件 官方github下载kubeedge地址 cloudcore.service文件下载地址 注意:下载对应的版本和arm架构 keadm-v1.6.1-linux-arm64.tar.gz 下面的2个文件可以不用下载,安装kubeedge时也会自动去下载到/etc/kubee…...

编程日记 2023/3/12 1:49:55

33--Vue-前端开发-使用Vue脚手架快速搭建项目

一、vue脚手架搭建项目 node的安装： 官方下载，一路下一步 node命令类似于python npm命令类似于pip 使用npm安装第三方模块，速度慢一些，需换成淘宝镜像 以后用cmpm代替npm的使用 npm install -g cnpm --registry=https://registry.npm.taobao.org安装脚手架： cnpm inst…...

编程日记 2023/3/12 1:48:51