利用圆上两点和圆半径求解圆心坐标
已知圆上两点P1,P2,坐标依次为 ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_1,y_1),(x_2,y_2) (x1,y1),(x2,y2),圆的半径为 r r r,求圆心的坐标。
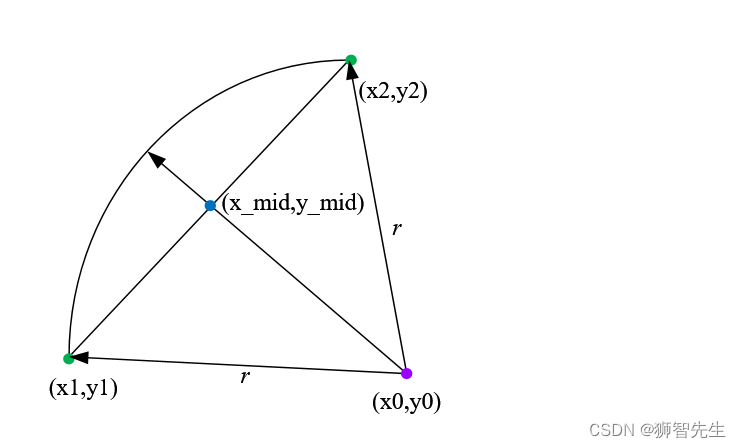
假定P1,P2为任意两点,则两点连成线段的中点坐标是
x m i d = ( x 1 + x 2 ) / 2 x_{mid} = (x_1+x_2)/2 xmid=(x1+x2)/2
y m i d = ( y 1 + y 2 ) / 2 y_{mid} = (y_1+y_2)/2 ymid=(y1+y2)/2
P1,P2连线的斜率是
k = ( y 1 − y 2 ) / ( x 1 − x 2 ) k = (y_1-y_2)/(x_1-x_2) k=(y1−y2)/(x1−x2)
P1,P2连线的垂线斜率为
m = − 1 / k m = -1/k m=−1/k
则,圆心所在的直线方程是
y − y m i d = m ∗ ( x − x m i d ) y-y_{mid} = m * (x - x_{mid}) y−ymid=m∗(x−xmid)
圆心 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)同时满足
( x 0 − x 1 ) 2 + ( y 0 − y 1 ) 2 = r 2 (x_0-x_1)^2+(y_0-y_1)^2=r^2 (x0−x1)2+(y0−y1)2=r2和 y 0 − y m i d = m ∗ ( x 0 − x m i d ) y_0-y_{mid} = m * (x_0 - x_{mid}) y0−ymid=m∗(x0−xmid)
或
( x 0 − x 2 ) 2 + ( y 0 − y 2 ) 2 = r 2 (x_0-x_2)^2+(y_0-y_2)^2=r^2 (x0−x2)2+(y0−y2)2=r2和 y 0 − y m i d = m ∗ ( x 0 − x m i d ) y_0-y_{mid} = m * (x_0 - x_{mid}) y0−ymid=m∗(x0−xmid)
将直线方程
y 0 = m ∗ ( x 0 − x m i d ) − y m i d y_0 = m*(x_0 -x_{mid})-y_{mid} y0=m∗(x0−xmid)−ymid
代入圆的公式,
得到
( x 0 − x 1 ) 2 + [ m ∗ ( x 0 − x m i d ) + y m i d − y 1 ] 2 = r 2 (x_0-x_1)^2+[m * (x_0-x_{mid})+y_{mid}-y_1]^2=r^2 (x0−x1)2+[m∗(x0−xmid)+ymid−y1]2=r2
展开,
x 0 2 − 2 x 0 x 1 + x 2 2 + m 2 x 0 2 + 2 m x 0 ∗ ( y m i d − m ∗ x m i d − y 1 ) + ( y m i d − m ∗ x m i d − y 1 ) 2 = r 2 x_0^2-2x_0x_1+x_2^2+m^2x_0^2+2mx_0*(y_{mid}-m*x_{mid}-y_1)+(y_{mid}-m*x_{mid}-y_1)^2=r^2 x02−2x0x1+x22+m2x02+2mx0∗(ymid−m∗xmid−y1)+(ymid−m∗xmid−y1)2=r2
整理,
( 1 + m 2 ) x 0 2 + [ 2 m ( y m i d − m ∗ x m i d − y 1 ) − 2 x 1 ] ∗ x 0 + ( y m i d − m ∗ x m i d − y 1 ) 2 + x 1 2 − r 2 = 0 (1+m^2)x_0^2+[2m(y_{mid}-m*x_{mid}-y_1)-2x_1]*x_0+(y_{mid}-m*x_{mid}-y_1)^2+x_1^2-r^2 = 0 (1+m2)x02+[2m(ymid−m∗xmid−y1)−2x1]∗x0+(ymid−m∗xmid−y1)2+x12−r2=0
令,
A = 1 + m 2 A= 1+m^2 A=1+m2
B = 2 m ( y m i d − m ∗ x m i d − y 1 ) − 2 x 1 B= 2m(y_{mid}-m*x_{mid}-y_1)-2x_1 B=2m(ymid−m∗xmid−y1)−2x1
C = ( y m i d − m ∗ x m i d − y 1 ) 2 + x 1 2 − r 2 C= (y_{mid}-m*x_{mid}-y_1)^2+x_1^2-r^2 C=(ymid−m∗xmid−y1)2+x12−r2
则,
x 0 = − B ± B 2 − 4 A C 2 A x_0=\frac{-B± \sqrt{B^2-4AC}}{2A} x0=2A−B±B2−4AC
y 0 = m ∗ ( x 0 − x m i d ) + y m i d y_0= m*(x_0-x_{mid})+y_{mid} y0=m∗(x0−xmid)+ymid
x_1 = 2
y_1 = 4
x_2 = 4
y_2 = 2
r = 2
if (x_1 - x_2 == 0):print('横坐标相同,求解可能出错')exit()
else:x_mid = (x_1 + x_2) / 2y_mid = (y_1 + y_2) / 2k = (y_1-y_2)/(x_1-x_2)m = -1/kA = 1 + m**2B = 2 * m *(y_mid - m * x_mid - y_1)- 2 * x_1C = (y_mid - m * x_mid - y_1)**2 + x_1**2 - r**2print(A, B, C)x_c1 = (-B + ((B**2-4*A*C)**0.5))/(2*A)x_c2 = (-B - ((B**2-4*A*C)**0.5))/(2*A)y_c1 = m * (x_c1 - x_mid) + y_midy_c2 = m * (x_c2 - x_mid) + y_midprint('圆心坐标:',(x_c1,y_c1))print('圆心坐标:',(x_c2,y_c2))
运行结果:

InsCode
相关文章:

利用圆上两点和圆半径求解圆心坐标
已知圆上两点P1,P2,坐标依次为 ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_1,y_1),(x_2,y_2) (x1,y1),(x2,y2),圆的半径为 r r r,求圆心的坐标。 假定P1,P2为任意两点,则两点连成线段的中点坐标是 x m i …...

从ChatGPT代码执行逃逸到LLMs应用安全思考
摘要 11月7日OpenAI发布会后,GPT-4的最新更新为用户带来了更加便捷的功能,包括Python代码解释器、网络内容浏览和图像生成能力。这些创新不仅开辟了人工智能应用的新境界,也展示了GPT-4在处理复杂任务方面的惊人能力。然而,与所有…...

Python入门-基础知识-变量
1.标识符与关键字 Python语言规定,标识符由字母、数字和下画线组成,且不允许以数字开头。合法的标识符可以 是student_1、 addNumber、num等,而3number、2_student等是不合法的标识符。在使用标识符时应注意以下几点。 (1)命名时应遵循见名知…...
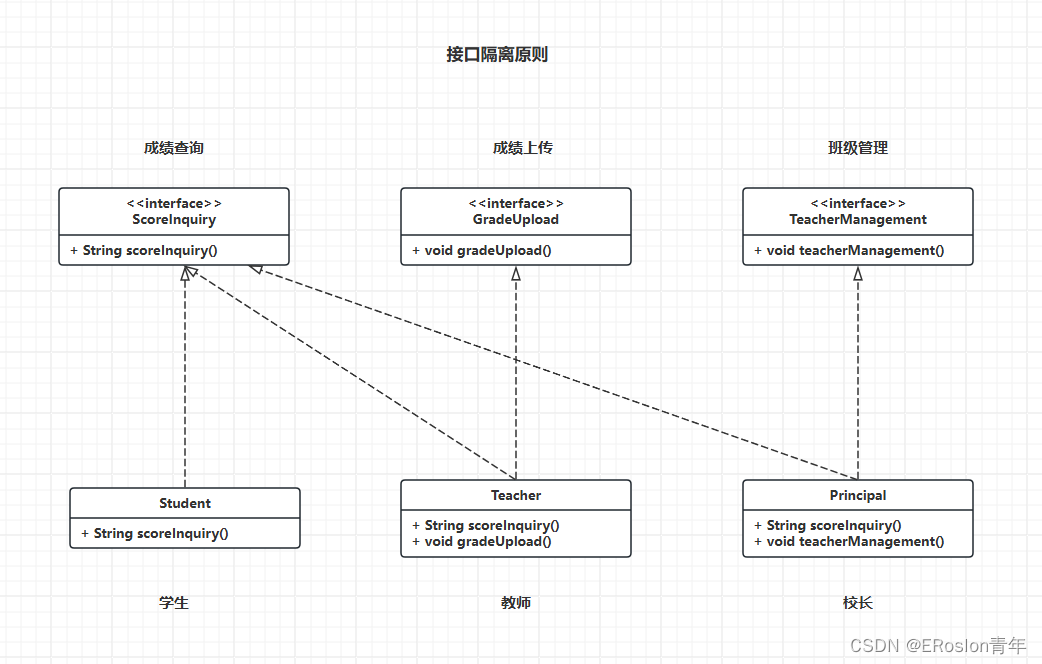
设计模式原则——接口隔离原则
设计模式原则 设计模式示例代码库地址: https://gitee.com/Jasonpupil/designPatterns 接口隔离原则 要求程序员尽量将臃肿庞大的接口拆分为更小的和更具体的接口,让接口中只包含客户感兴趣的方法接口隔离原则的目标是降低类或模块之间的耦合度&…...

MySQL数据库——在Centos7环境安装
MySQL在Centos7环境安装 1.切换root用户 安装与卸载中,用户全部切换成为root,安装好后,普通用户也能使用 2.卸载不要的环境 要将自己环境中有关mysql的全都删除,避免安装过程中被影响 ps axj | grep mariadb 先检查是否有mari…...

怎样规避液氮容器内部结霜的问题
液氮容器内部结霜问题一直是我们在使用液氮储存罐时遇到的一个棘手难题。液氮的极低温度使得容器内部很容易产生结霜现象,这不仅影响了容器的正常使用,还可能对内部样品或设备造成损坏。因此,如何有效规避液氮容器内部结霜问题成为了每个使用…...

冶金工业5G智能工厂工业物联数字孪生平台,推进制造业数字化转型
冶金工业5G智能工厂工业物联数字孪生平台,推进制造业数字化转型。传统生产方式难以满足现代冶金工业的发展需求,数字化转型成为必然趋势。通过引入5G、工业物联网和数字孪生等先进技术,冶金工业可以实现生产过程智能化、高效化和绿色化&#…...

一文入门机器学习参数调整实操
作者前言: 通过向身边的同事大佬请教之后,大佬指点我把本文的宗旨从“参数调优”改成了“参数调整”。实在惭愧,暂时还没到能“调优”的水平,本文只能通过实操演示“哪些操作会对数据训练产生影响”,后续加深学习之后,…...

基于51单片机的银行排队呼叫系统设计
一.硬件方案 本系统是以排队抽号顺序为核心,客户利用客户端抽号,工作人员利用叫号端叫号;通过显示器及时显示当前所叫号数,客户及时了解排队信息,通过合理的程序结构来执行排队抽号。电路主要由51单片机最小系统LCD12…...

JXCategoryView的使用总结
一、初始化 -(JXCategoryTitleView *)categoryView{if (!_categoryView) {_categoryView [[JXCategoryTitleView alloc] init];_categoryView.delegate self;_categoryView.titleDataSource self;_categoryView.averageCellSpacingEnabled NO; //是否平均分配项目之间的间…...

Centos9 安装VBox增强功能问题
安装步骤 更新gcc 首先手动更新gcc,防止无法兼容最新版本的内核,我这里将gcc 11更新到gcc 13 1.首先更新当前gcc和支持 yum install -y gcc gcc-c 2.下载新版本gcc压缩包 wget http://ftp.gnu.org/gnu/gcc/gcc-13.1.0/gcc-13.1.0.tar.gz 解压到usr ta…...

【JVM】Java虚拟机运行时数据分区介绍
JVM 分区(运行时数据区域) 文章目录 JVM 分区(运行时数据区域)前言1. 程序计数器2. Java 虚拟机栈3. 本地方法栈4. Java 堆5. 方法区6. 运行时常量池7. 直接内存 前言 之前在说多线程的时候,提到了JVM虚拟机的分区内存…...
)
大数据面试题之Kafka(2)
目录 Kafka的工作原理? Kafka怎么保证数据不丢失,不重复? Kafka分区策略 Kafka如何尽可能保证数据可靠性? Kafka数据丢失怎么处理? Kafka如何保证全局有序? 生产者消费者模式与发布订阅模式有何异同? Kafka的消费者组是如何消费数据的 Kafka的…...
)
前端面试题(基础篇十一)
一、DOCTYPE 的作用是什么? <!DOCTYPE> 声明一般位于文档的第一行,它的作用主要是告诉浏览器以什么样的模式来解析文档。一般指定了之后会以标准模式来进行文档解析,否则就以兼容模式进行解析。在标准模式下,浏览器的解析规…...
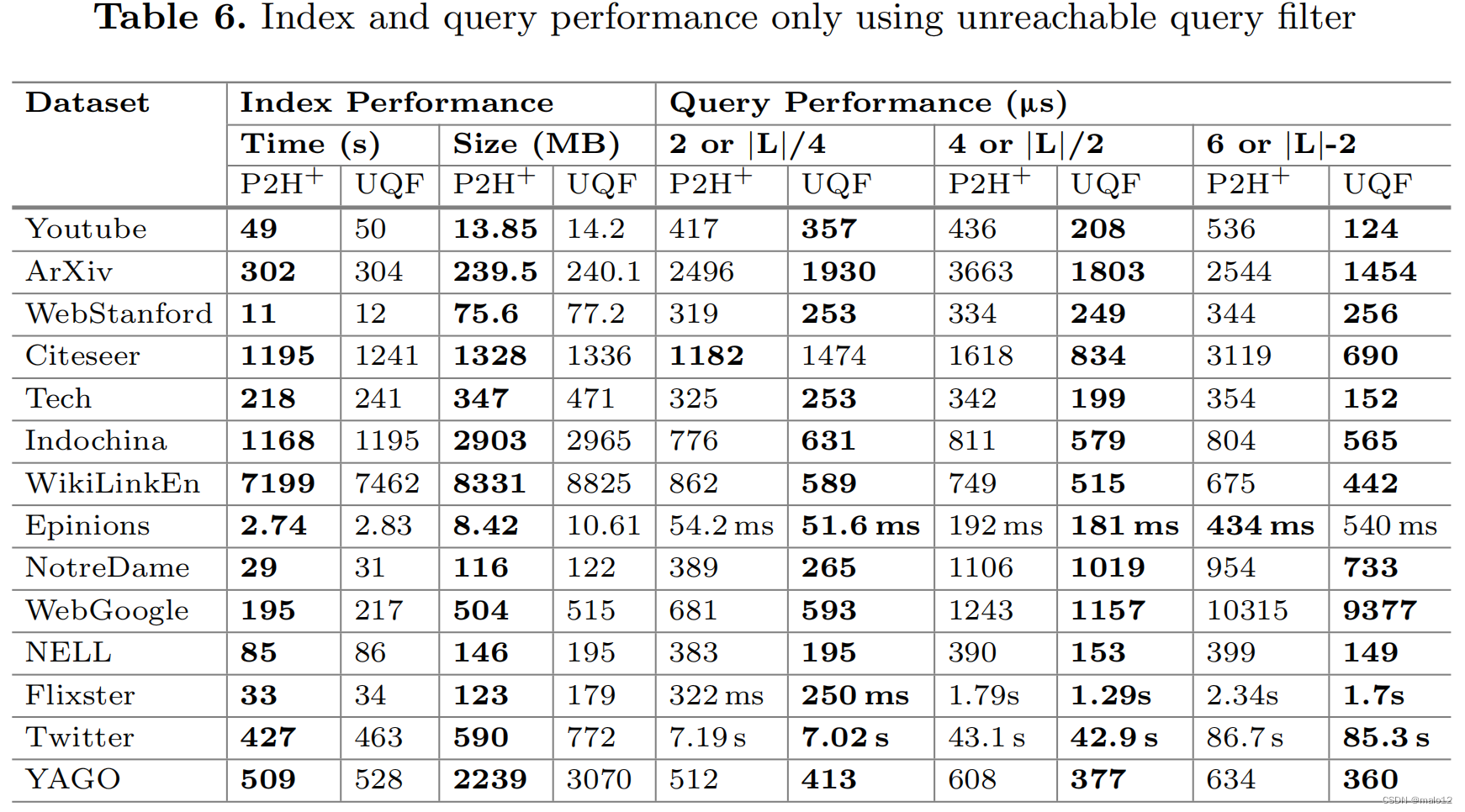
【论文阅读】Answering Label-Constrained Reachability Queries via Reduction Techniques
Cai Y, Zheng W. Answering Label-Constrained Reachability Queries via Reduction Techniques[C]//International Conference on Database Systems for Advanced Applications. Cham: Springer Nature Switzerland, 2023: 114-131. Abstract 许多真实世界的图都包含边缘标签…...

Git Flow 工作流学习要点
Git Flow 工作流学习要点 Git Flow — 流程图Git Flow — 操作指令优点:缺点:Git Flow 分支类型Git Flow 工作流程简述关于 feature 分支关于 Release 分支关于 hotfix 分支 总结 Git Flow — 流程图 图片来源:https://nvie.com/posts/a-succ…...

blender 快捷键 常见问题
一、快捷键 平移视图:Shift 鼠标中键旋转视图:鼠标中键缩放视图:鼠标滚动框选放大模型:Shift B线框预览和材质预览切换:Shift Z 二、常见问题 问题:导入模型成功,但是场景中看不到。 解…...

HTTP详解:TCP三次握手和四次挥手
一、TCP协议概述 TCP协议是互联网协议栈中传输层的核心协议之一,它提供了一种可靠的数据传输方式,确保数据包按顺序到达,并且没有丢失或重复。TCP的主要特点包括: 面向连接:TCP在传输数据之前需要建立连接。可靠传输&…...

详解HTTP:有了HTTP,为何需要WebSocket?
在日常生活中,HTTP 常用于请求数据。例如,当你打开一个天气预报网站时,浏览器会发送一个 HTTP 请求到服务器,请求当前的天气数据,服务器返回响应,浏览器解析并显示这些数据。 但是,当涉及到需要…...

Spring Boot 启动流程是怎么样的
引言 SpringBoot是一个广泛使用的Java框架,旨在简化基于Spring框架的应用程序的开发过程。在这篇文章中,我们将深入探讨SpringBoot应用程序的启动流程,了解其背后的机制。 Spring Boot 启动概览 SpringBoot应用程序的启动通常从一个包含 m…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
