仓库选址问题【数学规划的应用(含代码)】阿里达院MindOpt
本文主要讲述使用MindOpt工具优化仓库选址的数学规划问题。
视频讲解👈👈👈👈👈👈👈👈👈
一、案例场景
仓库选址问题在现代物流和供应链管理中具有重要的应用。因为仓库的位置直接影响到货物的运输成本、交货时间和库存量等因素。
涉及的行业有:
农业的农产品的输出和分销需要适当的仓储设备,尤其对于易腐烂的农产品,像水果、蔬菜等等。在制造业中,为存放一些原料、半成品或成品,制造业需在生产基地附近或靠近市场的地方建立仓库。
零售业的零售商通常需要在城市中心或人口密集区域附近设计仓库,以便商品的快速配送。
电子商务、食品行业以及医药行业等应用非常广泛。
通常考虑以下因素:运输成本,考虑与供应商和消费市场的距离;地理位置、土地成本等等。
二、数学规划
仓库选址问题也可以使用数学规划的方法。数学规划是一种数学优化方法,主要是寻找变量的取值在特定的约束情况下使我们的决策目标得到一个最大或最小值的决策。常见规划方法有线性规划、整数规划还有非线性规划。
工具:
MindOpt优化求解器:帮我们求解大规模数据的数学规划问题。
三、问题描述
某公司有很多家商店,要建造多个工厂为商店供货。不同工厂库存容量和建设成本不同,每个商店的需求和每个工厂向商店运输商品的成本也不同。如何选择最优的工厂建造方案和供货方案使得总成本最低?

这个例题主要考虑了以下四点因素:
一是仓库建设成本,包括土地成本、建筑成本,以及设备成本等。在实际应用中,这个成本因素通常是已知的。因为仓库建设成本比较稳定,所以通过市场价格或预算确定。
二是库存成本,是在仓库中维护和管理存货所需成本,成本因素包括储存成本、订单处理成本,还有库存租金、保险费用等。在实际的应用中,需要调查和分析得出成本因素,以便在模型中考虑成本的影响。
三是运输成本,将货物从仓库运输到客户所需的成本,因素通常有运输距离、运输方式、运输时间、运输成本等,通常经过一定调查和分析之后得出,可通过运输网络模型、运输成本数据库或者实地考察等方式确定。
四是交通需求,是客户对货物的需求量,这个数据可通过客户的订单量、历史数据等方式获取。在实际的应用中,需要考虑客户对不同商户的需求量,以便在模型中考虑到对总成本的影响。
代码解析
使用工具:
- MindOpt Studio 云建模平台**,**在线开发调试,免下载
- MindOpt APL(MAPL)建模语言编程**,**代数建模语言,语法与数学公式相近
声明集合、参数

声明的集合:「PLANTS」是工厂的类型,「STORES」是拥有的商店数量。

声明的参数是每个工厂建造的成本和每个工厂的库存容量。
声明变量

在这个问题中,可以控制的决策变量是建造什么类型的工厂和由哪个工厂运输商品给哪个商店。所以声明两个二进制的决策变量,用0和1分别代表不建造不运输和建造运输两个场景,“1”表示建造工厂,“0”表示不建筑工厂。
声明目标函数

我们的决策目标是最小化成本。所以需要计算建造成本、运输成本,也就每个工厂建造的代价,以及建造的每个工厂+每个工厂运输商品到对应店的代价之和最小化。
声明约束

- 我们声明的约束在实际生活中,每个商店有不同工厂的选择。为了简化问题,我们假设每个商店只能选择一个工厂供货,

- 第二条约束是建造工厂才能提供货物给商店,由于第一条约束是每个商店只能选择一个工厂供货,所以我们需建造的工厂数量至少满足将商品提供给每个商店,也就是至少有一个工厂可以向所有的商店供货。比如A工厂,A工厂的二进制是“1”,即建造A工厂,然后A工厂提供给每一个商店的二进制状态也是“1”,也就是至少有一个工厂建造。

- 第三条约束是每间工厂的库存不能小于其所提供的商店需求之和,每个工厂储存的商品数量有限,一个工厂商品清空后,需要从另一个工厂运输。比如A工厂的库存是40,从A工厂运输到商店1、2、3,那么1、2、3商店需要的商品数量不能超过A工厂的库存数量。
结果解析
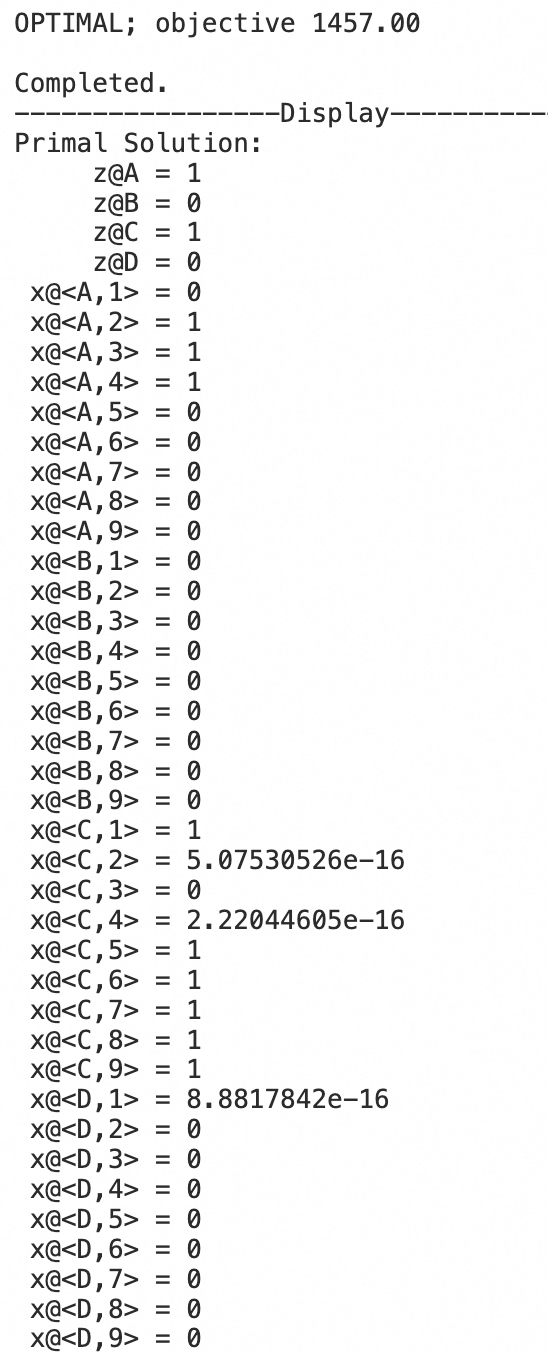

我们对这个问题进行求解。最后得出的结果是最小化的总成本是1457。我们建造了一个A工厂、一个C工厂,二号商店是由A工厂供货,三号商店也是由A工厂供货。
四、内容回顾
我们本期主要讲述的是仓库选址问题,考虑仓库的建设成本、运输成本、库存成本、交货需求四个因素最小化总成本。

扫描二维码获取源代码
仓库选址规划-MindOpt Studio
相关文章:

仓库选址问题【数学规划的应用(含代码)】阿里达院MindOpt
本文主要讲述使用MindOpt工具优化仓库选址的数学规划问题。 视频讲解👈👈👈👈👈👈👈👈👈 一、案例场景 仓库选址问题在现代物流和供应链管理中具有重要的应用。因为仓库…...
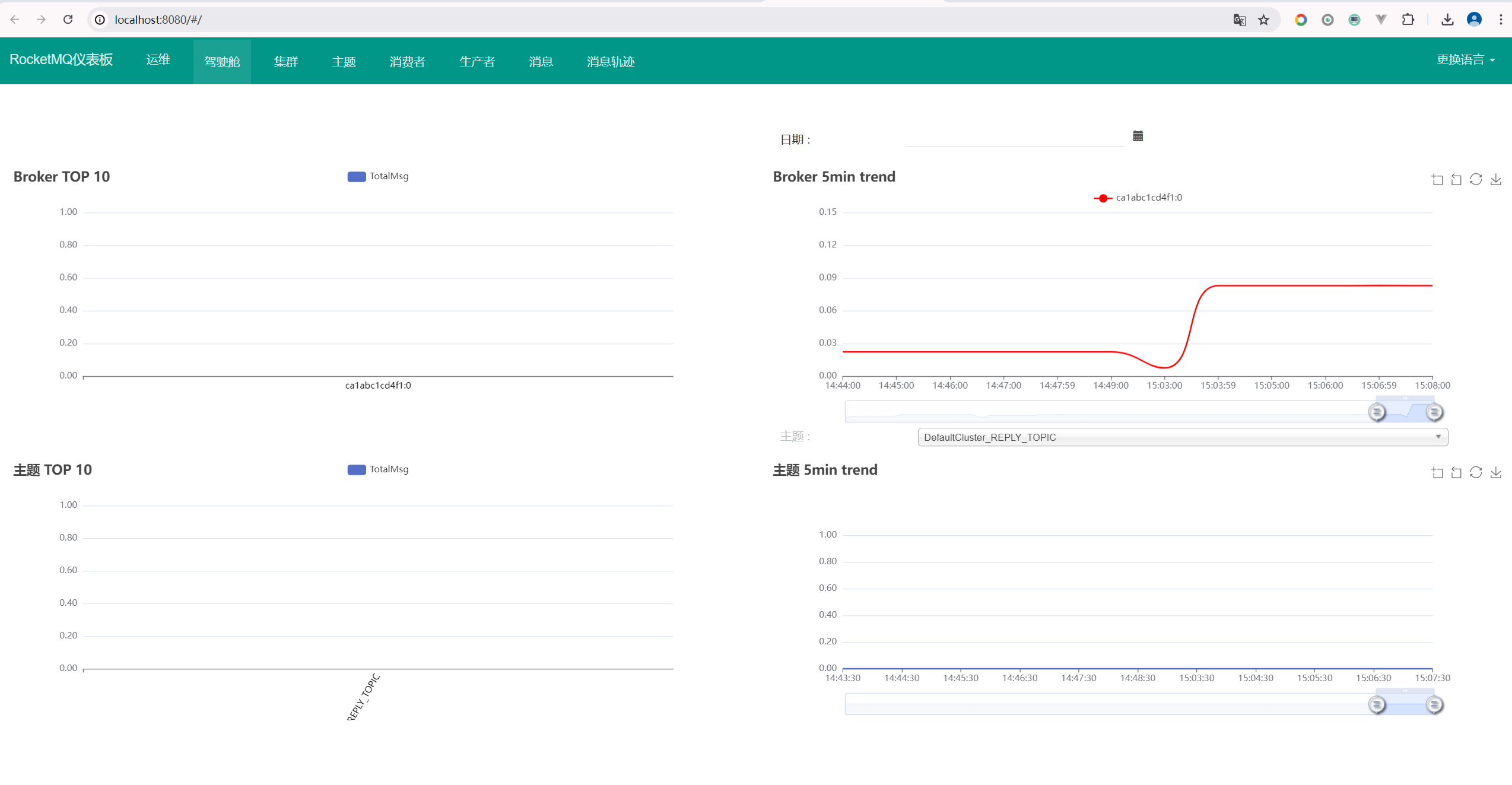
Docker Compose 一键快速部署 RocketMQ
Apache RocketMQ是一个开源的分布式消息中间件系统,最初由阿里巴巴开发并贡献给Apache软件基金会。RocketMQ提供了高性能、高可靠性、高扩展性和低延迟的消息传递服务,适用于构建大规模分布式系统中的消息通信和数据同步。 RocketMQ支持多种消息模型&am…...
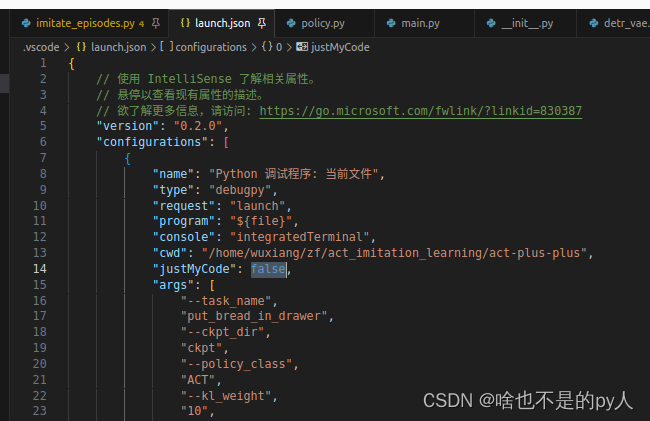
Vscode lanuch.json
Intro 使用launch.json 能够方便的运行需要传很多参数的代码文件 如下: import math import argparse # 1、导入argpase包def parse_args():parse argparse.ArgumentParser(descriptionCalculate cylinder volume) # 2、创建参数对象parse.add_argument(--rad…...

Golang开发:构建支持并发的网络爬虫
Golang开发:构建支持并发的网络爬虫 随着互联网的快速发展,获取网络数据成为了许多应用场景中的关键需求。网络爬虫作为一种自动化获取网络数据的工具,也因此迅速崛起。而为了应对日益庞大的网络数据,开发支持并发的爬虫成为了必…...
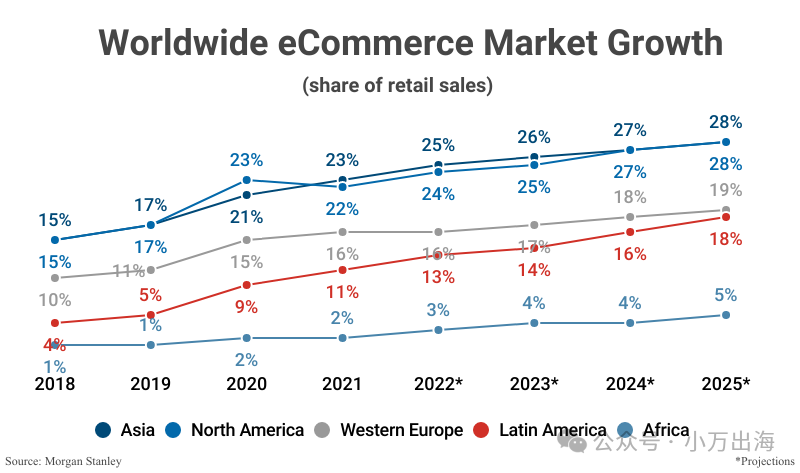
2024年跨境电商关键数据统计:市场规模将达到1.976万亿美元
预计2024年跨境电商消费市场规模将达到1.976万亿美元,占全球网上销售总额的31.2%。这一数据无疑展示了跨境电商市场的巨大潜力和迅猛增长趋势。 全球跨境电商的现状与未来 现状 2023年,全球跨境电商市场规模预计达到1.56万亿美元,占全球电子…...

联想至像M3070DNA打印机加粉及清零方法
基本参数: 产品类型:黑白激光多功能商用一体机(打印/复印/扫描) 网络功能:支持有线网络打印 最大处理幅面:A4 双面功能:自动 打印速度:30页/分钟(高速激光打印&…...

通过nginx去除 api url前缀 并保持后面剩余的url不变向后台请求
如 我前台浏览器向后台请求的接口是 http://127.0.0.1:5099/api/sample/sample/getbuttonlist 实际的请求接口传向 http://192.168.3.71:5099/sample/sample/getbuttonlist 方法是向config中加入下面这样一个server server {listen 5099;location /api/ {rewrite ^/a…...

AI技术在现代社会中的广泛应用及其影响
目录 前言: 一、AI技术在医疗领域的应用 二、AI技术在教育领域的应用 三、AI技术在工业领域的应用 四、AI技术在金融领域的应用 五、AI技术在生活领域的应用 前言: 随着科技的不断发展,人工智能(AI)技术逐渐成为人…...

VBA 批量变换文件名
1. 页面布局 在“main”Sheet中按照下面的格式编辑。 2. 实现代码 Private wsMain As Worksheet Private intIdx As LongPrivate Sub getExcelBookList(strPath As String)Dim fso As ObjectDim objFile As ObjectDim objFolder As ObjectSet fso = CreateObject("Scrip…...

OpenHarmony 5.0 纯血鸿蒙系统
OpenHarmony-v5.0-Beta1 版本已于 2024-06-20 发布。 OpenHarmony 5.0 Beta1 版本标准系统能力持续完善,ArkUI 完善了组件通过 C API 调用的能力;应用框架细化了生命周期管理能力,完善了应用拉起、跳转的能力;分布式软总线连接能力…...
)
计算机网络地址划分A-E(自学)
1、网络地址组成 (1)物理地址MAC(Media Access Control Address) 网卡生产商分配,全球唯一,48/64位二进制 (2)逻辑地址IP(Internet Protocol) 网络层地址,用于在不同网…...

js导入导出
好久没有学习新的知识点了,今天开始学一下前端的知识点。直接在vscode里面编写,然后从基本的前端知识开始。 JS的导入导出 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"…...
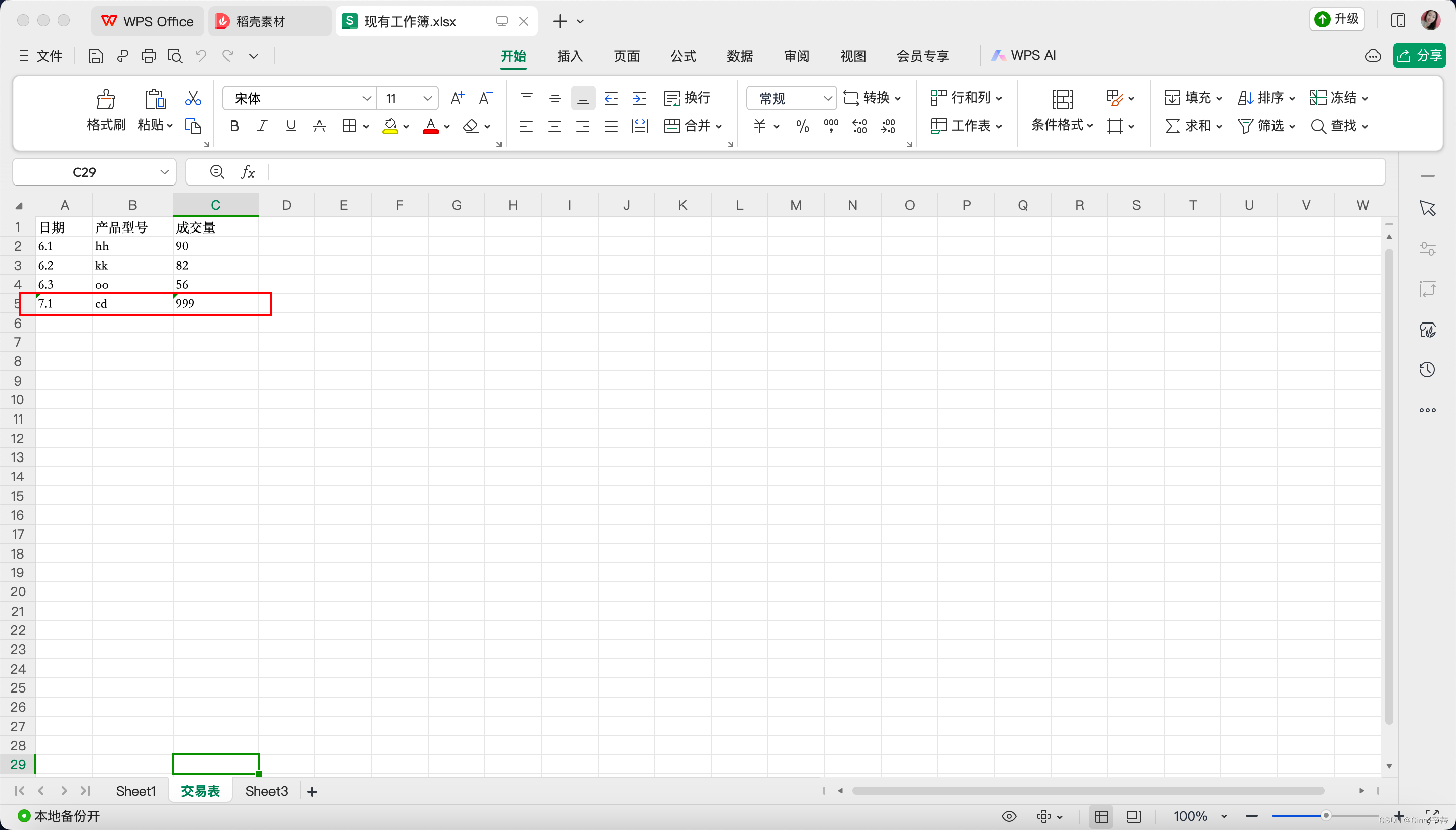
python办公自动化之excel
用到的库:openpyxl 实现效果:读取单元格的值,写入单元格 代码: import openpyxl # 打开现有工作簿 workbookopenpyxl.load_workbook(现有工作簿.xlsx) # 选择一个工作表 sheetworkbook[交易表] # 读取单元格的值 cell_valueshe…...

生命在于学习——Python人工智能原理(2.5.1)
五、Python的类与继承 5.1 Python面向对象编程 在现实世界中存在各种不同形态的事物,这些事物之间存在各种各样的联系。在程序中使用对象来映射现实中的事物,使用对象之间的关系描述事物之间的联系,这种思想用在编程中就是面向对象编程。 …...
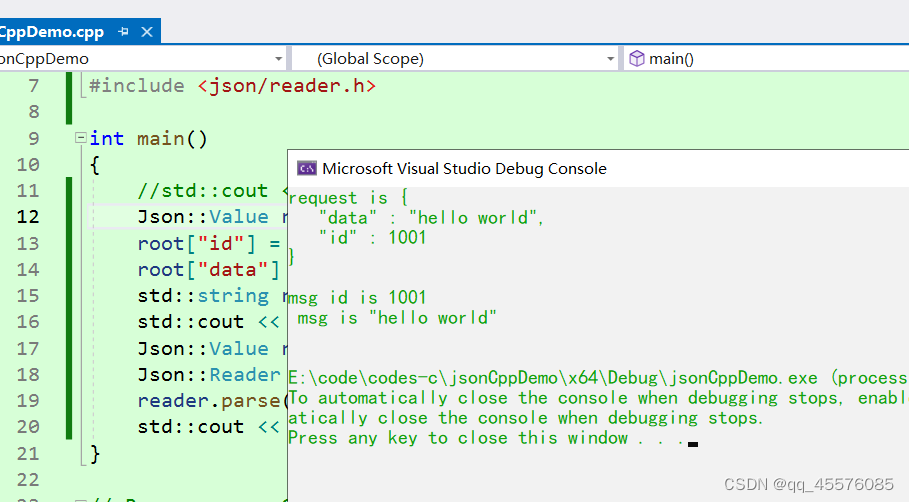
visual studio 2022配置和使用jsoncpp
下载 jsoncpp下载位置: GitHub - open-source-parsers/jsoncpp: A C library for interacting with JSON. 编译库 1、下载完成之后解压 2、在解压文件的makefiles文件下有个vs71,在vs71中有visual studio项目,不过这里的项目是visual stud…...

Spring Boot中的动态数据源切换
Spring Boot中的动态数据源切换 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天,我们将探讨如何在Spring Boot中实现动态数据源切换的技术。动态…...

npm error code EUNSUPPORTEDPROTOCOL 解决
更换包管理工具 npm i -g pnpm pnpm install pnpm run dev 参考 https://blog.csdn.net/qq_42592823/article/details/137541827...
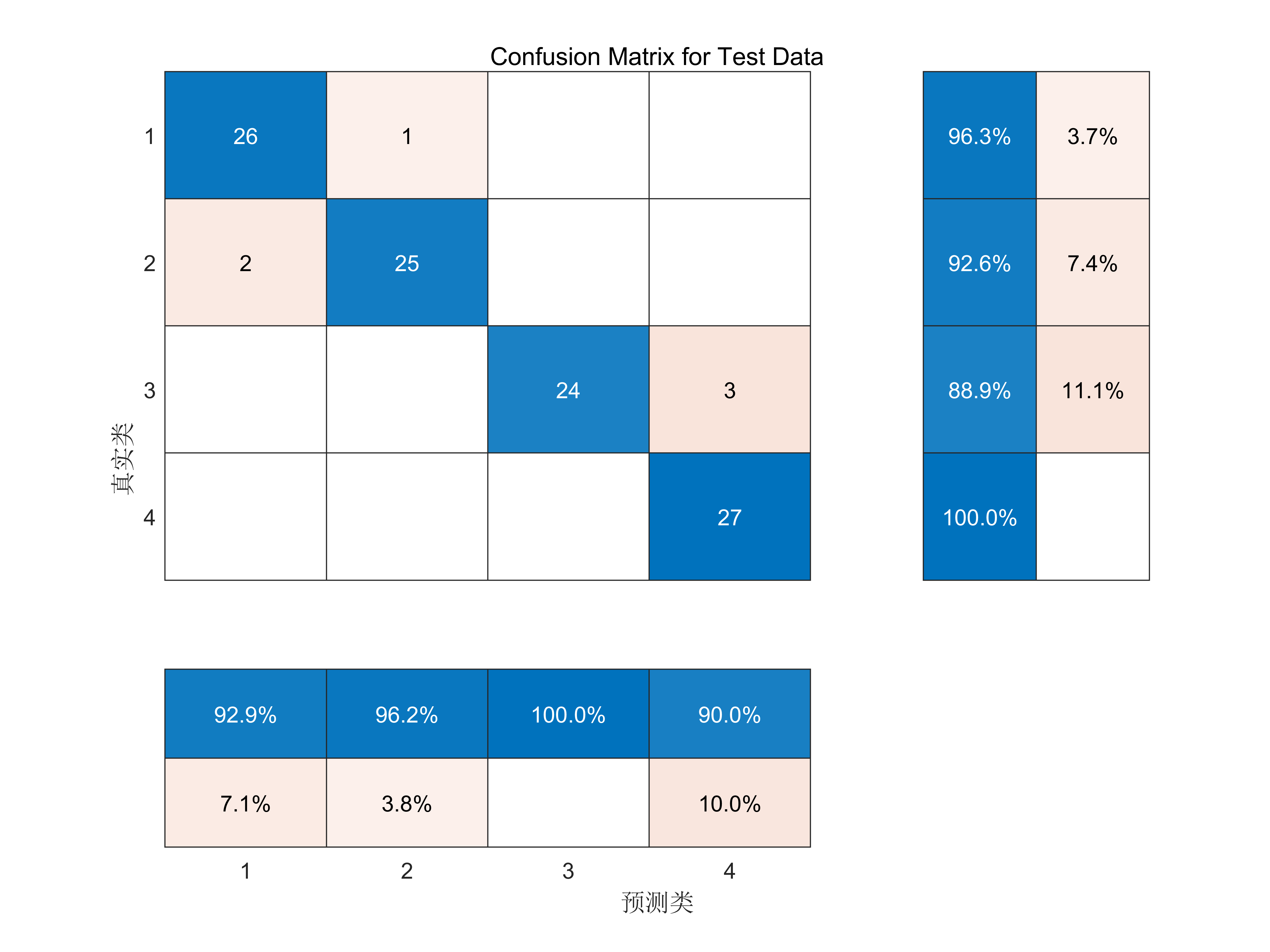
基于改进天鹰优化算法(IAO)优化支持向量机(SVM)数据分类预测(IAO-SVM)
改进天鹰优化算法(IAO)见:【智能优化算法】改进的AO算法(IAO)-CSDN博客 支持向量机(SVM)数据分类预测:基于支持向量机(SVM)的数据分类预测-CSDN博客 代码原理 基于改进天鹰优化算法(IAO)优化支持向量机(SVM…...

【数学建模】—【Python库】—【Numpy】—【学习】
目录 编辑 1. NumPy安装 2. ndarray对象 1. 创建ndarray 1.从列表或元组创建: 2.使用内置函数创建: 2. ndarray属性 3. 数组运算 1. 基本运算 2. 数学函数 3.统计函数 4. 数组索引与切片 1. 一维数组索引与切片 2.多维数组索引与切片 5.…...

C语言一些逆置算法
目录 整数逆置 数组逆置 矩阵转置 整数逆置 如7234变为4327 int Reversed(int n){int x,reversed_n0;while(n!0){xn%10; reversed_nreversed_n*10x;nn/10;}return reversed_n; }数组逆置 将数组{1,2,3,4,5,6}逆置为{6,5,4,3,2,1} void Reverse(int a[],int l,int r){w…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
