定积分定义求极限专题
文章目录
- 定积分定义求极限问题的描述
- 解决方法
- 真题实践(持续更新中,未完结)
定积分定义求极限问题的描述
在定积分定义求极限中,我们可能存在的问题
- 被积函数不会找
- 积分区间不会定(只会[0,1]的)
- 根本不知道“补系数”
- 只会f(i/n)的情况
定积分定义,简单来说就是底*高,无穷累加。
从0到n,均分变为1/n就是底,f(i/n)就是它对应的高,由于均分后已经很微小了,所以这个高只要保证在这样的一个小区间上即可。最后再累加。
上述就是定积分定义的最简单理解
∫ 0 1 f ( x ) d x = lim n → ∞ ∑ i = 1 n f ( i n ) 1 n \int \limits_{0}^{1}f\left(x\right)dx = \lim \limits_{n\rightarrow ∞}\sum \limits_{i = 1}^{n}f\left(\frac{i}{n}\right)\frac{1}{n} 0∫1f(x)dx=n→∞limi=1∑nf(ni)n1
现在待解决的问题就是如何根据后面的无穷项的数列极限,写成前面的定积分的形式。
解决方法
给出方法论:
- 找被积函数在于找变化的部分,将变化的部分写成x
- 确定积分区间,积分区间的确定,就看变化量的极限,它的第一项的极限就是下限,第n项的极限就是它的上限
- 确定底,也就是1/n需不需要补系数,用积分区间/实际项数。比如积分区间是0到1,但是根据规律发现只有偶数,那么它实际项数就是n/2,用(1-0)/(n/2),最后得到2/n,如果原先的系数是1/n,则需要将它的系数改为2/n,并在前面补系数2
补充两点:
1️⃣删去有限项不改变数列极限
2️⃣变化的部分,当然是越简单越好
没看懂很正常,真题实践会逐步掌握
真题实践(持续更新中,未完结)
真题实践部分由浅入深
1. lim n → ∞ 1 n ( s i n 1 n + s i n 2 n + s i n 3 n + . . . s i n n n ) 1.\lim \limits_{n\rightarrow ∞}\frac{1}{n}\left(sin\frac{1}{n} + sin\frac{2}{n} + sin\frac{3}{n} + ...sin\frac{n}{n}\right) 1.n→∞limn1(sinn1+sinn2+sinn3+...sinnn)
解析:
观察可知本题中的变化量是sin里面的数,并且前面给出1/n,大胆使用定积分定义。
1.括号里面的改成sinx,确定了被积函数。
2.积分区间,1/n就是就是0,n/n就是1
在这里非常值得注意的点是,积分区间的确定是根据变化部分确定的,这里可不是sin0和sin1,而是0和1
3.补系数,区间1,一共n项,就是1/n,不需要补系数
答案如下:
∫ 0 1 sin x d x \int \limits_{0}^{1}\sin xdx 0∫1sinxdx
2. lim n → ∞ ( 1 n + 1 + 1 n + 2 + 1 n + 3 + . . . 1 n + n ) 2.\lim \limits_{n\rightarrow ∞}\left(\frac{1}{n + 1} + \frac{1}{n + 2} + \frac{1}{n + 3} + ...\frac{1}{n + n}\right) 2.n→∞lim(n+11+n+21+n+31+...n+n1)
解析:
观察不难发现是分母1,2,3发生变化。我们首先要整理这个式子,让这个式子除了发生变化的量,其他均是常数,故分母同除n,提出一个1/n
lim n → ∞ 1 n ( 1 1 + 1 n + 1 1 + 2 n + 1 1 + 3 n + . . . 1 1 + n n ) \lim \limits_{n\rightarrow ∞}\frac{1}{n}\left(\frac{1}{1 + \frac{1}{n}} + \frac{1}{1 + \frac{2}{n}} + \frac{1}{1 + \frac{3}{n}} + ...\frac{1}{1 + \frac{n}{n}}\right) n→∞limn1(1+n11+1+n21+1+n31+...1+nn1)
1.确定被积函数,把1/n写成x,故被积函数就是1/(1+x)
2.确定区间,1/n是0,n/n是1,积分区间0到1
3.确定系数,区间是1,一共n项,系数1/n,不用补系数
答案如下:
∫ 0 1 1 1 + x d x \int \limits_{0}^{1}\frac{1}{1 + x}dx 0∫11+x1dx
相关文章:

定积分定义求极限专题
文章目录 定积分定义求极限问题的描述解决方法真题实践(持续更新中,未完结) 定积分定义求极限问题的描述 在定积分定义求极限中,我们可能存在的问题 被积函数不会找积分区间不会定(只会[0,1]的)根本不知道“补系数”…...
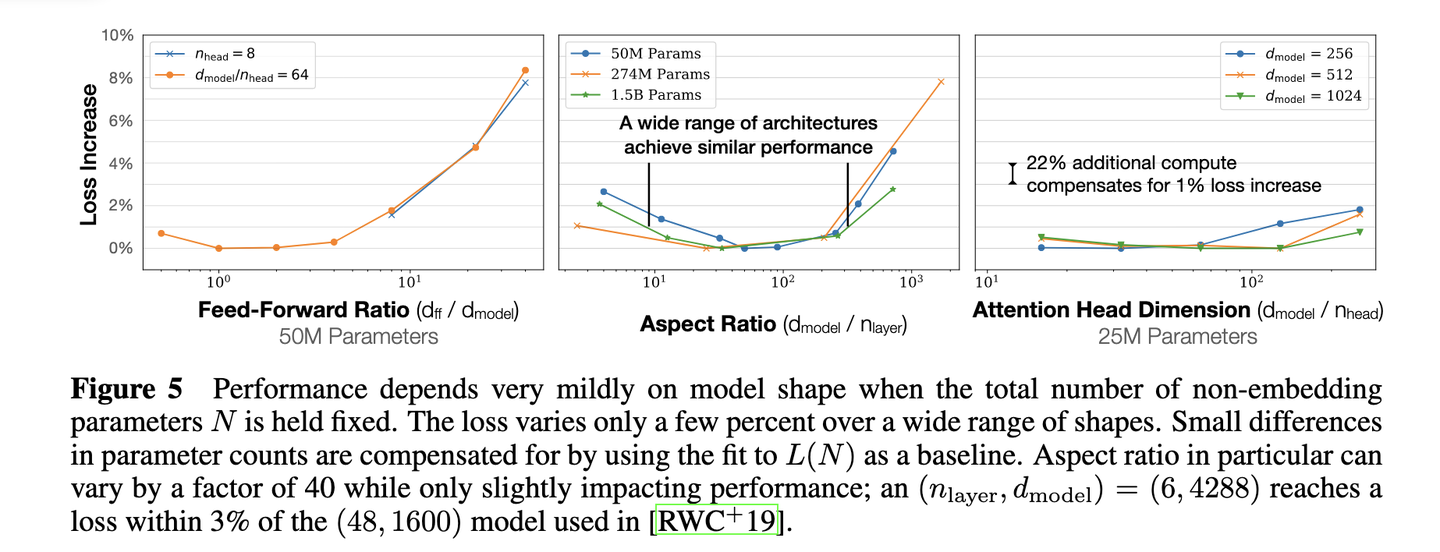
LLaMA:挑战大模型Scaling Law的性能突破
实际问题 在大模型的研发中,通常会有下面一些需求: 计划训练一个10B的模型,想知道至少需要多大的数据?收集到了1T的数据,想知道能训练一个多大的模型?老板准备1个月后开发布会,给的资源是100张A100,应该用多少数据训多大的模型效果最好?老板对现在10B的模型不满意,想…...

vue3 +elementPlus上传照片墙
获取到照片字符串然后push到fileList对应的URL中 if (formData.value.pictures) {let zz formData.value.pictures.split(",")zz.forEach((item) > {fileList.value.push({ url: item })})}对应表单 <el-form-item label"内容详情图"><el-up…...

Charles网络抓包工具安装和web抓包(一)
目录 概述 抓包工具对比 安装 下载 web抓包配置 按键说明 前言-与正文无关 生活远不止眼前的苦劳与奔波,它还充满了无数值得我们去体验和珍惜的美好事物。在这个快节奏的世界中,我们往往容易陷入工作的漩涡,忘记了停下脚步&#…...
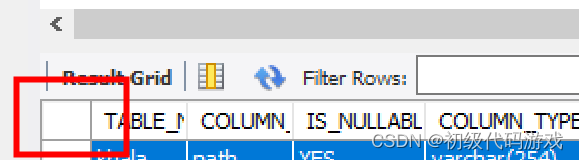
mysql workbench使用schema视图导出表和列结构到excel
目的:导出所有表和列的名字和注释 很多时候没有正规的数据库文档,为了快速交流啊,需要一个快捷的基础。数据库建表的时候可能有注释,也可能没有注释。有当然好,查看注释就能清楚很多,没有的话最好一个一个补…...
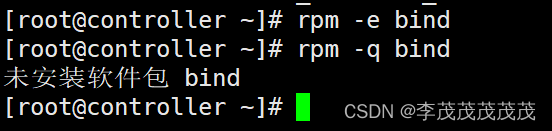
Linux操作系统--软件包管理(保姆级教程)
RPM软件包的管理 大多数linux的发行版本都是某种打包系统。软件包可以用来发布应用软件,有时还可以发布配置文件。他们比传统结构的.tar和.gz存档文件有几个优势。如它们能让安装过程尽可能成为不可分割的原子操作。 软件包的安装程序会备份它们改动过的文件。如果…...

【uniapp】HBuilderx中uniapp项目运行到微信小程序报错Error: Fail to open IDE
HBuilderx中uniapp项目运行到微信小程序报错Error: Fail to open IDE 问题描述 uniapp开发微信小程序,在HBuilderx中运行到微信开发者工具时报错Error: Fail to open IDE 解决方案 1. 查看微信开发者工具端服务端口是否开放 打开微信开发者工具选择࿱…...

Rust详解日志
详解日志 相比起监控,日志好理解的多:在某个时间点向指定的地方输出一条信息,里面记录着重要性、时间、地点和发生的事件,这就是日志。 注意,本文和 Rust 无关,我们争取从一个中立的角度去介绍何为日志 日…...

某麦网自动刷新抢票脚本——手机端(高级版)
某麦网自动刷新抢票脚本——电脑端 小白操作-抵制黄牛–需要更好用更高级关注获取 如何用Python自动抢大麦网演出票? 在数字化时代,购票已经成为我们生活的一部分,无论是音乐会、话剧、体育赛事还是各种展览,抢票几乎成了一项“…...
 —— 触发器)
【MySQL】(基础篇十八) —— 触发器
触发器 本文学习什么是触发器,为什么要使用触发器以及如何使用触发器,还介绍创建和使用触发器的语法。 MySQL语句在需要时被执行,存储过程也是如此。但是,如果你想要某条语句(或某些语句)在事件发生自动执…...

[19] Opencv_CUDA应用之 基于形状的对象检测与跟踪
Opencv_CUDA应用之 基于形状的对象检测与跟踪 形状可以用作全局特征检测具有不同形状的物体,可以是直线、多边形、圆形或者任何其他不规则形状利用对象边界、边缘和轮廓可以检测具有特定形状的对象本文将使用Canny边缘检测算法和Hough变换来检测两个规则形状,即线和圆1. Cann…...
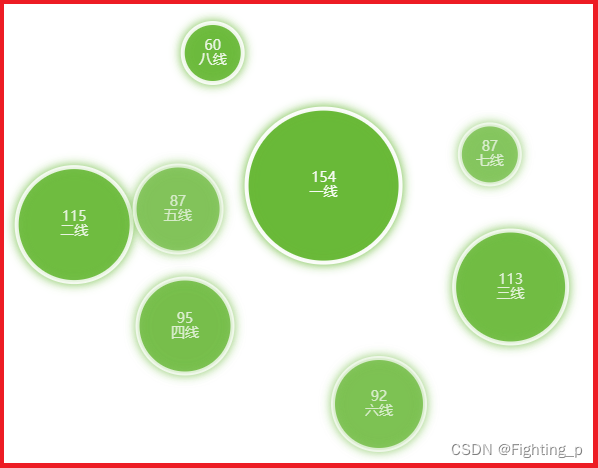
【Echarts】散点图 制作 气泡 类型图表
目录 需求主要代码效果展示注 需求 需参照设计图画出对应图表 主要代码 /**** 数据 ****/ this.dataList [...Array(8).keys()].map((item) > {return {ywlxmc: 业务类型 (item 1),sl: item > 4 ? 50 : 70} })/**** 气泡样式 ****/ const styleList [{offset: [56…...

深入理解Spring Boot的启动过程
深入理解Spring Boot的启动过程 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天,让我们一起深入探讨Spring Boot的启动过程。Spring Boot作为一…...
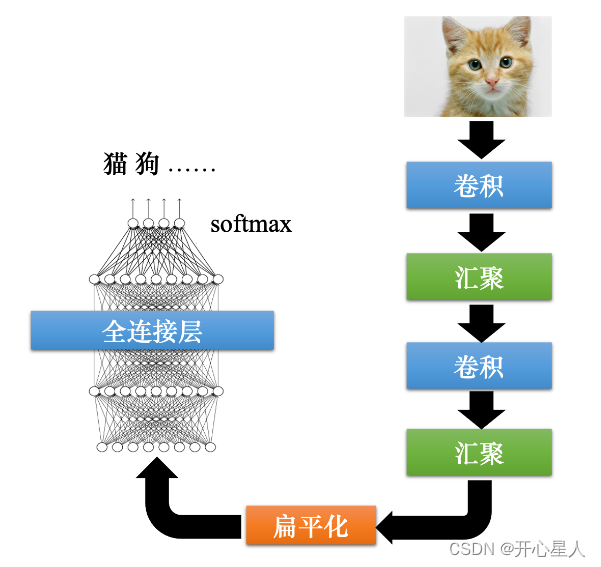
【深度学习】卷积神经网络CNN
李宏毅深度学习笔记 图像分类 图像可以描述为三维张量(张量可以想成维度大于 2 的矩阵)。一张图像是一个三维的张量,其中一维代表图像的宽,另外一维代表图像的高,还有一维代表图像的通道(channelÿ…...
游戏AI的创造思路-技术基础-深度学习(3)
继续填坑,本篇介绍深度学习中的长短期记忆网络~~~~ 目录 3.3. 长短期记忆网络(LSTM) 3.3.1. 什么是长短期记忆网络 3.3.2. 形成过程与运行原理 3.3.2.1. 细胞状态与门结构 3.3.2.2. 遗忘门 3.3.2.3. 输入门 3.3.2.4. 细胞状态更新 3.…...
)
贪心算法练习题(2024/6/24)
1K 次取反后最大化的数组和 给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组: 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。 重复这个过程恰好 k 次。可以多次选择同一个下标 i 。 以这种方式修改数组后,返回数组 可能的最…...
大厂程序员上班猝死成常态?
大家好,我是瑶琴呀,拥有一头黑长直秀发的女程序员。 近日,连续看到大厂程序员猝死、低血糖晕倒的新闻,同为程序员感到很难受。互联网加班成常态这是既定事实,尤其在这个内卷严重、经济不景气的环境中,加班…...

深度学习 —— 1.单一神经元
深度学习初级课程 1.单一神经元2.深度神经网络3.随机梯度下降法4.过拟合和欠拟合5.剪枝、批量标准化6.二分类 前言 本套课程仍为 kaggle 课程《Intro to Deep Learning》,仍按之前《机器学习》系列课程模式进行。前一系列《Keras入门教程》内容,与本系列…...

Android 12.0 通知发送过程源码分析-Framework
以下NotificationManagerService简称 NMS 1. 通知的发送: NotificationManager.notify(int id, Notification notification) 开始. 源码路径: /frameworks/base/core/java/android/app/NotificationManager.java/***发布通知以显示在状态栏中。 如果通知带有* 相同的 ID 已被…...

提防远程攻击:了解正向 Shell 和反向 Shell 确保服务器安全
前言 在当今网络安全形势日益复杂的环境中,了解正向 Shell 和反向 Shell 的工作原理和使用场景,对于保护你的服务器免受远程攻击至关重要。本文不仅深入解析这两种常见的远程控制技术,还将提供有效的防护建议,帮助你提升服务器的…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
