前缀和部分题目
前缀和
前缀和指数组的前 N项之和,是个比较基础的算法
例题
面试题 17.05. 字母与数字
给定一个放有字母和数字的数组,找到最长的子数组,且包含的字母和数字的个数相同。
返回该子数组,若存在多个最长子数组,返回左端点下标值最小的子数组。若不存在这样的数组,返回一个空数组。
示例 1:
输入: [“A”,“1”,“B”,“C”,“D”,“2”,“3”,“4”,“E”,“5”,“F”,“G”,“6”,“7”,“H”,“I”,“J”,“K”,“L”,“M”]
输出: [“A”,“1”,“B”,“C”,“D”,“2”,“3”,“4”,“E”,“5”,“F”,“G”,“6”,“7”]
示例 2:
输入: [“A”,“A”]
输出: []
提示:
array.length <= 100000
思路
使用前缀和+哈希
为字母则取1,数字为-1,即要求和为0的最大子数组。
前缀和表示第i个数及之前的所有数的和。哈希存储前缀和c第一次出现的位置i,循环时维护一个maxlen表示最大的子数组长度,start表示最长子数组起始下标。
初始化时,前缀和为0,下标为-1。遍历到i时,前缀和为sum,如果此时哈希表中没有关于前缀和为sum的记录,则更新indices[sum]=i。如果已有,则对比maxlen和i-indices[sum],如果i-indices[sum]较大,则maxlen更新为i-indices[sum],start更新为indices[sum]+1。
如果maxlen不为0,返回array中array[start]到array[start+maxlen]的部分。
代码
class Solution {
public:vector<string> findLongestSubarray(vector<string>& array) {int n=array.size();int sum=0;int maxlen=0;int start=-1;unordered_map<int,int> indices;indices[0]=-1;for(int i=0;i<n;i++){if(isalpha(array[i][0])){sum++;}else{sum--;}if(indices.find(sum)==indices.end()){indices[sum]=i;}else{if(i-indices[sum]>maxlen){maxlen=i-indices[sum];start=indices[sum]+1;}}}if(maxlen==0) return {};return vector<string>(array.begin()+start,array.begin()+start+maxlen);}
};
209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105
进阶:
如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。
思路
首先计算前缀和,presum[i]表示从0加到i-1的和,
对于遍历每个子数组的起始点nums[i],用二分搜索找到presum[j]-presum[i]大于或等于target的第一个下标j,遍历过程中维护最短子数组的长度minlen。
或者用滑动窗口做
代码
//前缀和+二分搜索
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int n=nums.size();int minlen=n+1;vector<int> presum(n+1,0);//presum[i]是从0加到i-1for(int i=0;i<n;i++){presum[i+1]=presum[i]+nums[i];}for(int i=0;i<n;i++){int l=i+1,r=n;while(l<r){int m=(l+r)/2;if(presum[m]-target<presum[i]){l=m+1;}else{r=m;}}if(presum[l]-target>=presum[i]){minlen=min(l-i,minlen);}}if(minlen>n) return 0;else return minlen;}
};
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int n=nums.size();int l=0,r=0;int sum=nums[0],minlen=n+1;while(r<n){while(sum<target&&r<n){if(++r<n) sum+=nums[r];}if(sum>=target){minlen=min(minlen,r-l+1);sum-=nums[l];l++;}else break;}return minlen<=n?minlen:0;}
};
相关文章:

前缀和部分题目
前缀和 前缀和指数组的前 N项之和,是个比较基础的算法 例题 面试题 17.05. 字母与数字 给定一个放有字母和数字的数组,找到最长的子数组,且包含的字母和数字的个数相同。 返回该子数组,若存在多个最长子数组,返回左…...
三天吃透MySQL面试八股文
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...

Giving You A guide to learning any topic faster than 95% of people
A guide to learning any topic faster than 95% of people: Richard Feynman was a physician who won the Nobel Prize in 1965. But he became known for his great lectures. Why? He was able to explain complex concepts in simple terms with these 4 steps: 1 • E…...
大白话MySQL是如何根据成本优化选择执行计划的?(中))
(七十七)大白话MySQL是如何根据成本优化选择执行计划的?(中)
上次我们讲完了全表扫描的成本计算方法,相信大家应该都理解了,其实还是比较简单的,今天我们来讲一下索引的成本计算方法,因为除了全表扫描之外,还可能多个索引都可以使用,但是当然同时一般只能用一个索引&a…...

原来CSS 也可以节流啊
Ⅰ、前言 「节流」 是为了减少请求的触发频率,不让用户点的太快,达到节省资源的目的 ;通常 我们采用 JS 的 定时器 setTimeout ,来控制点击多少秒才能在触发;其实 通过 CSS 也能达到 「节流」 的目的,下面…...

UE官方教程笔记03-功能、术语、操作简介
对官方教程视频[官方培训]03-UE功能、术语、操作简介 | 徐良安 Epic的笔记这一部分基本都是走马观花的简单介绍功能世界创建建模Mesh editingtool是一个全新的建模工具,具备大多数的主流建模软件的核心功能HOUDINI ENGINE FOR UNREALHoudini编辑器,可以用…...
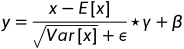
BN,LN,IN,GN的理解和用法
绿色区域表示将该区域作用域(四种方法都贯穿了w,h维度),即将该区域数值进行归一化,变为均值为0,标准差为1。BN的作用区域时N,W,H,表示一个batch数据的每一个通道均值为0,标准差为1;LN则是让每个数据的所有channel的均值…...
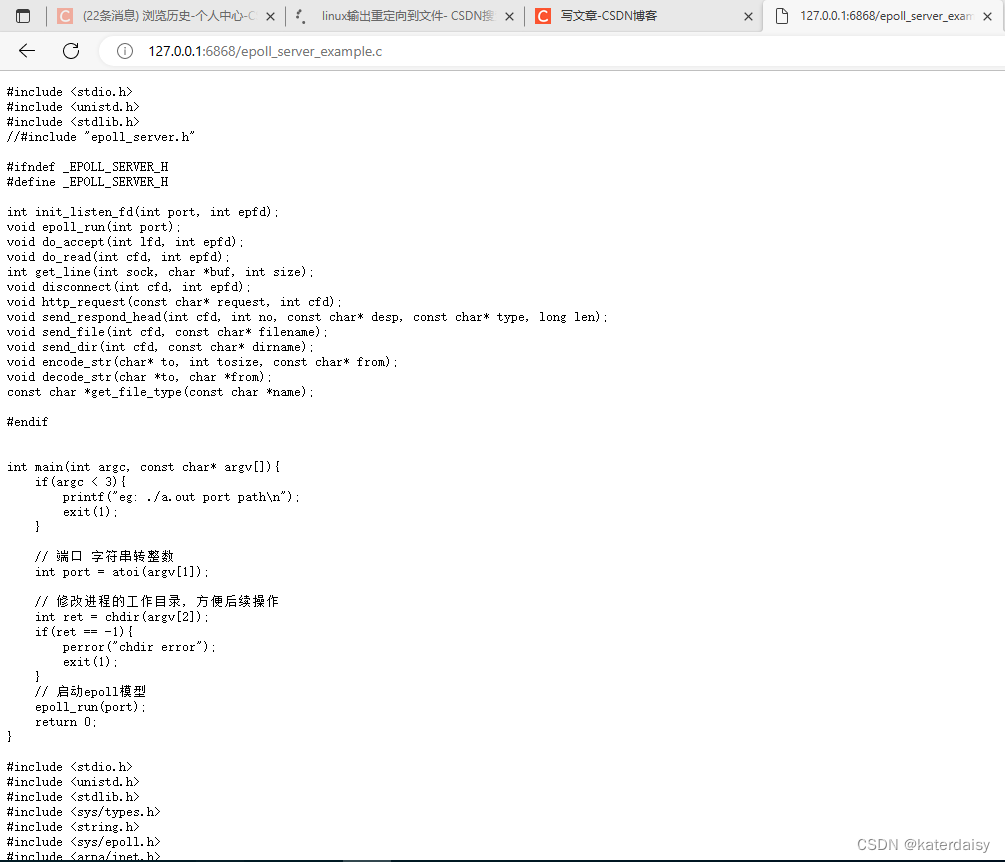
Linux:epoll模式web服务器代码,代码debug
源码: https://blog.csdn.net/weixin_44718794/article/details/107206136 修改的地方: 修改后代码: #include <stdio.h> #include <unistd.h> #include <stdlib.h> //#include “epoll_server.h” #ifndef _EPOLL_SER…...
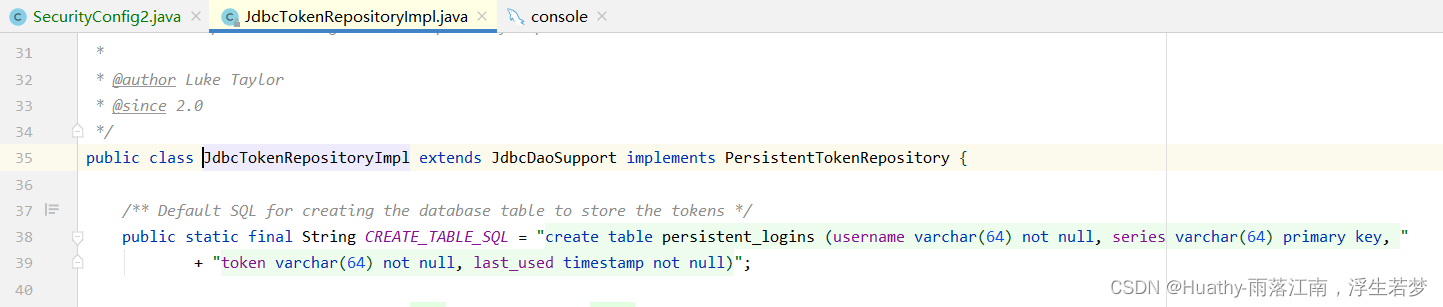
SpringSecurity学习(四)密码加密、RememberMe记住我
文章目录密码加密一、简介密码为什么要加密常见的加密解决方案PasswordEncoder详解DelegatingPasswordEncoder二、自定义加密方式1. 使用灵活的密码加密方案(BCryptPasswordEncoder)加密验证(推荐)需要在密码前指定加密类型{bcryp…...
vue专项练习
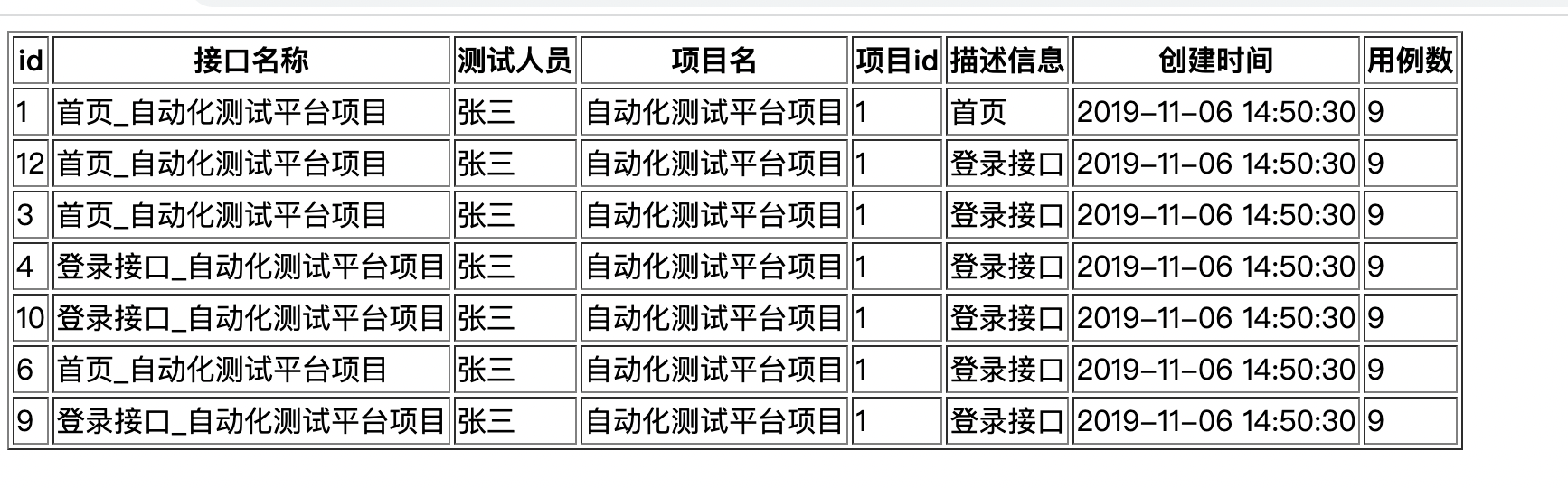
一、循环实现一个列表的展示及删除功能 1.1 列表展示 1、背景: 完成一个这样的列表展示。使用v-for 循环功能 id接口名称测试人员项目名项目ID描述信息创建时间用例数1首页喵酱发财项目a1case的描述信息2019/11/6 14:50:30102个人中心张三发财项目a1case的描述信…...

【笔试题】百度+美团
发工资 链接:https://www.nowcoder.com/questionTerminal/e47cffeef25d43e3b16c11c9b28ac7e8 来源:牛客网 小度新聘请了一名员工牛牛, 每个月小度需要给牛牛至少发放m元工资(给牛牛发放的工资可以等于m元或者大于m元, 不能低于m)。 小度有一些钞票资金…...

【8.索引篇】
索引分类 索引和数据就是位于存储引擎中: 按「数据结构」分类:Btree索引、Hash索引、Full-text索引。按「物理存储」分类:聚簇索引(主键索引)、二级索引(辅助索引)。按「字段特性」分类&#…...
MySQL InnoDB存储引擎锁与事务实现原理解析(未完成)
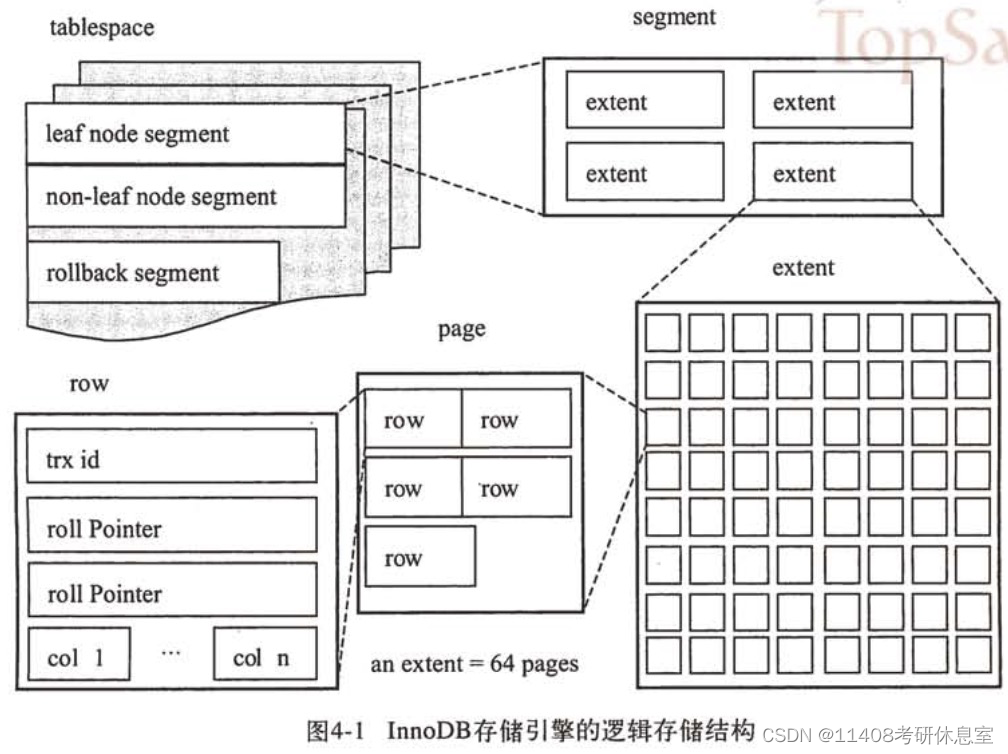
InnoDB MySQL存储引擎是基于表的,也就是说每张表可以选择不同的存储引擎。 InnoDB存储引擎的表是索引组织的,也就是数据即索引。 存储引擎文件 InnoDB引擎会包含RedoLog重做日志文件和TableSpace表空间文件。 表空间文件 默认表空间文件(…...
JAVA)
P1683 入门(洛谷)JAVA
题目描述: 不是任何人都可以进入桃花岛的,黄药师最讨厌像郭靖一样呆头呆脑的人。所以,他在桃花岛的唯一入口处修了一条小路,这条小路全部用正方形瓷砖铺设而成。有的瓷砖可以踩,我们认为是安全的,而有的瓷砖…...

yocto编译烧录和脚本解析
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、初始化构建目录二、imx-setup-release.sh脚本解析三、编译单独编译内核四、烧录总结前言 本篇文章主要讲解如何在下载好源码之后进行编译和yocto的脚本解析…...

Proteus 8.15安装包安装教程
Proteus介绍Proteus的介绍Proteus8.15安装包Proteus8.15安装教程Proteus的介绍 Proteus是英国著名的EDA工具(仿真软件),从原理图布图、代码调试到单片机与外围电路协同仿真,一键切换到PCB设计,真正实现了从概念到产品的完整设计。是世界上唯…...

Spring——AOP工作流程
AOP就是代理模式的开发简化 1.Spring容器启动 因为AOP是要将通知类作为一个bean对象交给spring进行管理的,还有经过通知类被增强的类。 此时还没有创建bean对象 2.读取所有切面配置中的切入点 在下面这段代码中,定义了两个切入点,但是只…...
、notify_one()、notify_all()的使用。)
c++11多线程之condition_variable、wait()、notify_one()、notify_all()的使用。
系列文章目录 文章目录系列文章目录前言一、基本概念1.1 std::condition_variable1.2 wait()函数1.2.1 wait()带第二个参数1.2.2 wait()不带第二个参数1.2.3 当其他线程用notify_one()或notify_all()1.3 notify函数二、代码实例总结前言 C11多线程&…...

skywalking扩展实现 —— 监控数据的动态上报
把标题名整高大上一些,来掩盖需求的奇葩。 0. 目录1. 需求背景2. 需求描述3. 优势4. 实现4.1 扩展点4.2 配置项5. 优化6. 提醒7. 补充 - 关于微服务8. 参考1. 需求背景 过去一段时间,接手了一个迭代了数年的"基于微服务架构"搭建的产品。 自…...

【GoF 23】23种设计模式与OOP七大原则概述
1. 什么是GoF 23? GoF 23也就是23种设计模式。1995年GoF(Gang of Four,四人组/四人帮)合作出版了《设计模式:可复用面向对象软件的基础》一书,一共收录了23种设计模式,从此梳理了软件设计模式领…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
