【二叉树广度优先遍历和深度优先遍历】
文章目录
- 一、二叉树的深度优先遍历
- 0.建立一棵树
- 1. 前序遍历
- 2.中序遍历
- 3. 后序遍历
- 二、二叉树的广度优先遍历
- 层序遍历
- 三、有关二叉树练习
一、二叉树的深度优先遍历
学习二叉树结构,最简单的方式就是遍历。
所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉
树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。
遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
0.建立一棵树
typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;}BTNode;int main()
{BTNode* A = (BTNode*)malloc(sizeof(BTNode));A->data = 'A';A->left = NULL;A->right = NULL;BTNode* B = (BTNode*)malloc(sizeof(BTNode));B->data = 'B';B->left = NULL;B->right = NULL;BTNode* C = (BTNode*)malloc(sizeof(BTNode));C->data = 'C';C->left = NULL;C->right = NULL;BTNode* D = (BTNode*)malloc(sizeof(BTNode));D->data = 'D';D->left = NULL;D->right = NULL;BTNode* E = (BTNode*)malloc(sizeof(BTNode));E->data = 'E';E->left = NULL;E->right = NULL;A->left = B;A->right =C;B->left = D;B->right = E;return 0;
}
结果如下:

1. 前序遍历
访问根结点的操作发生在遍历其左右子树之前。
先访问根节点,再到左子节点,然后到右子节点。
根->左->右

//后序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){return;}printf("%c ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}

2.中序遍历
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
先访问左子树,再访问根,再到右子树
左–>根–>右

由于NULL不打印出来,故结果为 D->B->E->A->C
代码如下:
//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}
代码分析:

3. 后序遍历
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
先访问左子节点,再访问右子节点,最后访问根。
左–>右–>根
分析结果如下
打印结果为: D E B C A
代码如下:
//后续遍历
void PostOrder(BTNode* root)
{if (!root){return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);
}
代码分析如下:

二叉树的前序,中序,后序遍历结果如下:

二、二叉树的广度优先遍历
层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1
层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点
以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
层序遍历就是一层一层地访问,先访问第一层, 再访问第二层。
核心思想是上一层出去带下一层进来
实现的过程不使用递归实现,使用队列实现:
借助队列先进先出的特点

队列源代码:
typedef struct BinaryTreeNode* QDataType;typedef struct QueueNode
{QDataType data;struct QueueNode* next;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;int size;
}Queue;void QueueInit(Queue* pq)
{assert(pq);pq->head = NULL;pq->tail = NULL;pq->size = 0;
}void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* del = cur;cur = cur->next;free(del);//del = NULL;}pq->head = pq->tail = NULL;pq->size = 0;
}void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->data = x;newnode->next = NULL;if (pq->tail == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;
}void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* del = pq->head;pq->head = pq->head->next;free(del);}pq->size--;
}QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head == NULL && pq->tail == NULL;
}实现层序遍历过程中二叉树借助队列源代码:
//借助队列的先进先出来实现层级递进
void LevelOrder(BTNode* root)
{//核心思路,上一层出的时候带下一层Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%c ", front->data);//访问下一层if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}
三、有关二叉树练习
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。
该完全二叉树的前序序列为( )
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
解析:
已知该树为完全二叉树,第一层只有一个节点,第二层有2个节点,第三层有4个节点…
容易知道该完全二叉树的高度是4,还原可得:
根据前序序列遍历,先根,再左子节点,再右子节点,选A
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A E
B F
C G
D H
解析:由二叉树的前序遍历可知,根节点为E。
此时已经得出答案,但我想还原这棵树
由中序遍历可知:E是根节点,那么E左边的所有节点为HFI,右边的所有节点为JKG
由前序遍历可知,E到F,说明F是E的左子节点,由中序遍历,H到F,说名H是F的左子节点。到这里可以还原二叉树的左半部分了,右半部分同理。
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,
则二叉树前序遍历序列为____。
A adbce
B decab
C debac
D abcde
解析:
由二叉树的后序遍历可知根节点为a。
由中序序列可知a的左子节点只有b,右子节点右dce
又由后序遍历往前推,可知c是a的右子节点
到这里已经可以推出整棵树了
所以该树的前序序列为abcde,选D
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,
则按层次输出(同一层从左到右)的序列为
A FEDCBA
B CBAFED
C DEFCBA
D ABCDEF
解析:
由二叉树的后序遍历可知,根节点为F,由中序遍历可知,根节点F无右子节点。
F的左节点有ABCDE
又因为前序和中序都相同,那么只有一种情况:
所以答案选A
相关文章:

【二叉树广度优先遍历和深度优先遍历】
文章目录一、二叉树的深度优先遍历0.建立一棵树1. 前序遍历2.中序遍历3. 后序遍历二、二叉树的广度优先遍历层序遍历三、有关二叉树练习一、二叉树的深度优先遍历 学习二叉树结构,最简单的方式就是遍历。 所谓二叉树遍历(Traversal)是按照某种特定的规则ÿ…...
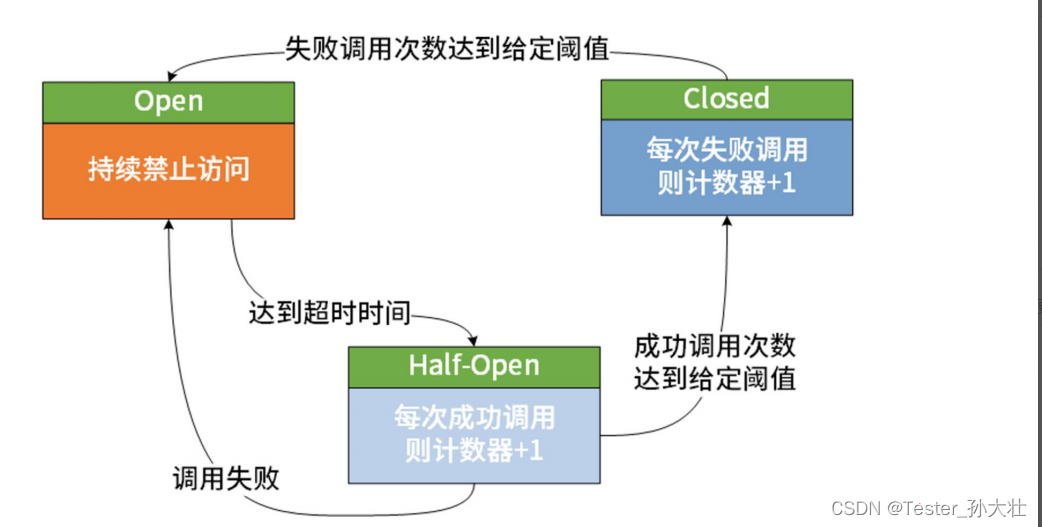
Spring Cloud微服务架构必备技术
单体架构 单体架构,也叫单体应用架构,是一个传统的软件架构模式。单体架构是指将应用程序的所有组件部署到一个单一的应用程序中,并统一进行部署、维护和扩展。在单体架构中,应用程序的所有功能都在同一个进程中运行,…...
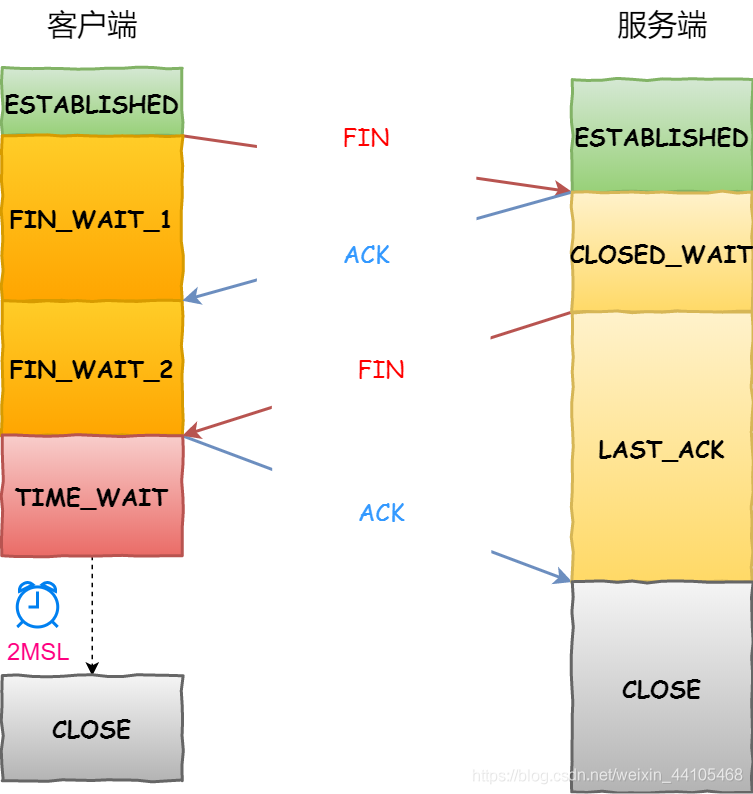
TCP三次握手与四次挥手(一次明白)
TCP基本信息 默认端口号:80 LINUX中TIME_WAIT的默认时间是30s TCP三次握手 三次握手过程:每行代表发起握手到另一方刚刚收到数据包时的状态 客户端服务端客户端状态服务端状态握手前CLOSELISTEN客户端发送带有SYN标志的数据包到服务端一次握手SYN_SENDLISTEN二次握手服务端发送…...

pyside6@Mouse events实例@QApplication重叠导致的报错@keyboardInterrupt
文章目录报错内容鼠标事件演示报错内容 在pyside图形界面应用程序开发过程中,通常只允许运行一个实例 假设您重复执行程序A,那么可能会导致一些意向不到的错误并且,从python反馈的信息不容易判断错误的真正来源 鼠标事件演示 下面是一段演示pyside6的鼠标事件mouseEvent对象…...

订单30分钟未支付自动取消怎么实现?
目录了解需求方案 1:数据库轮询方案 2:JDK 的延迟队列方案 3:时间轮算法方案 4:redis 缓存方案 5:使用消息队列了解需求在开发中,往往会遇到一些关于延时任务的需求。例如生成订单 30 分钟未支付࿰…...

< 开源项目框架:推荐几个开箱即用的开源管理系统 - 让开发不再复杂 >
文章目录👉 SCUI Admin 中后台前端解决方案👉 Vue .NetCore 前后端分离的快速发开框架👉 next-admin 适配移动端、pc的后台模板👉 django-vue-admin-pro 快速开发平台👉 Admin.NET 通用管理平台👉 RuoYi 若…...

内网渗透-基础环境
解决依赖,scope安装 打开要给cmd powershell 打开远程 Set-ExecutionPolicy RemoteSigned -scope CurrentUser; 我试了好多装这东西还是得科学上网,不然不好用 iwr -useb get.scoop.sh | iex 查看下载过的软件 安装sudo 安装git 这里一定要配置bu…...

Go语言学习的第一天(对于Go学习的认识和工具选择及环境搭建)
首先学习一门新的语言,我们要知道这门语言可以帮助我们做些什么?为什么我们要学习这门语言?就小wei而言学习这门语言是为了区块链,因为自身是php出身,因为php的一些特性只能通过一些算法模拟的做一个虚拟链,…...

C和C++到底有什么关系
C++ 读作”C加加“,是”C Plus Plus“的简称。顾名思义,C++是在C的基础上增加新特性,玩出了新花样,所以叫”C Plus Plus“,就像 iPhone 6S 和 iPhone 6、Win10 和 Win7 的关系。 C语言是1972年由美国贝尔实验室研制成功的,在当时算是高级语言,它的很多新特性都让汇编程序…...
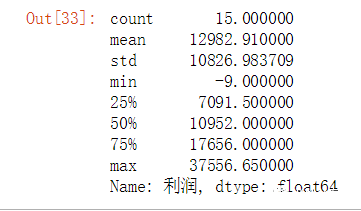
14个Python处理Excel的常用操作,非常好用
自从学了Python后就逼迫用Python来处理Excel,所有操作用Python实现。目的是巩固Python,与增强数据处理能力。 这也是我写这篇文章的初衷。废话不说了,直接进入正题。 数据是网上找到的销售数据,长这样: 一、关联公式:…...

async/await 用法
1. 什么是 async/await async/await 是 ES8(ECMAScript 2017)引入的新语法,用来简化 Promise 异步操作。在 async/await 出 现之前,开发者只能通过链式 .then() 的方式处理 Promise 异步操作。示例代码如下: import …...
好意外,发现永久免费使用的云服务器
原因就不说了,说一下过程,在百度搜pythonIDE的时候,发现了一个网站 https://lightly.teamcode.com/https://lightly.teamcode.com/ 就是这个网站,看见这个免费试用,一开始觉得没什么,在尝试使用的过程中发…...
VSCode使用技巧,代码编写效率提升2倍以上!
VSCode是一款开源免费的跨平台文本编辑器,它的可扩展性和丰富的功能使得它成为了许多程序员的首选编辑器。在本文中,我将分享一些VSCode的使用技巧,帮助您更高效地使用它。 1. 插件 VSCode具有非常丰富的插件生态系统,通过安装插…...
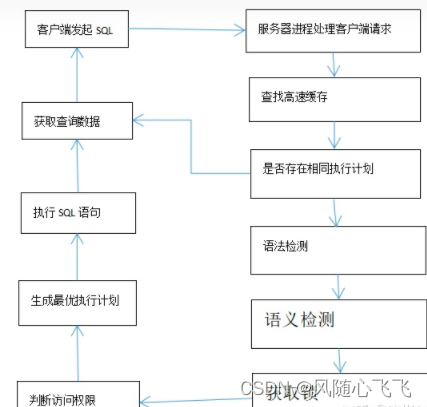
SQL执行过程详解
1 、用户在客户端执行 SQL 语句时,客户端把这条 SQL 语句发送给服务端,服务端的进程,会处理这条客户端的SQL语句。 2 、服务端进程收集到SQL信息后,会在进程全局区PGA 中分配所需内存,存储相关的登录信息等。 3 、客…...
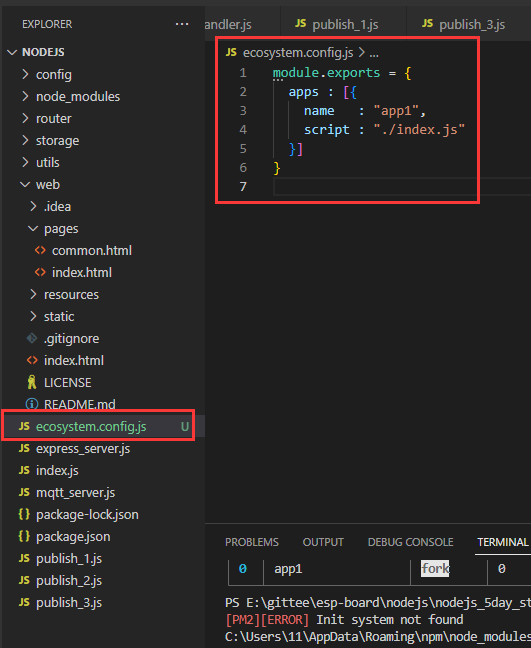
【物联网NodeJs-5天学习】第四天存储篇⑤ ——PM2,node.js应用进程管理器
【NodeJs-5天学习】第四天存储篇⑤ ——PM2,node.js应用进程管理器1. 前言2. 官方说明3. 安装PM24. PM2常用命令4.1 启动命令4.2 重新启动命令4.3 热重载命令4.4 停止命令4.5 删除命令4.6 查看进程运行状态4.4 显示某一个进程的具体信息4.8 显示日志信息4.9 终端监控…...

【C++学习】【STL】deque容器
dequeDouble Ended Queues(双向队列)deque和vector很相似,但是它允许在容器头部快速插入和删除(就像在尾部一样)。所耗费的时间复杂度也为常数阶O(1)。并且更重要的一点是,deque 容器中存储元素并不能保证所有元素都存储到连续的内…...

当 App 有了系统权限,真的可以为所欲为?
看到群里发了两篇文章,出于好奇,想看看这些个 App 在利用系统漏洞获取系统权限之后,都干了什么事,于是就有了这篇文章。由于准备仓促,有些 Code 没有仔细看,感兴趣的同学可以自己去研究研究,多多…...

vue3.js的介绍
一.vue.js简述 Vue是一套用于构建用户开源的MVVM结构的Javascript渐进式框架,尤雨溪在2015年10月27日发布了vue.js 1.0Eavangelion版本,在2016年9月30日发布了2.0Ghost in the Shell版本,目前项目由官方负责 vue的核心只关注图层࿰…...

【Three.js】shader特效 能量盾
shader特效之能量盾前言效果噪点图主要代码index.htmldepth-fs.jsdepth-vs.jsshield-fs.jsshield-vs.js相关项目前言 效果噪点图 为了可以自定义能量球的效果,这里使用外部加载来的噪点图做纹理,省去用代码写特效的过程。 主要代码 index.html <…...

【6000字长文】需求评审总是被怼?强烈推荐你试试这三招
前段时间和一个合作部门的产品新人沟通需求,结束的时候,他问了我一个问题,“你在产品新人阶段,最害怕做的事情是什么”? 我不假思索的回答说,“需求评审,是曾经最不想面对的环节,甚至在评审之前几个小时就开始心跳加速了。当然这也是产品修炼路上的必经之路,其实只要掌…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...



