Python协作运动机器人刚体力学解耦模型
🎯要点
🎯腿式或固定式机器人模型 | 🎯网格、点云和体素网格碰撞检测 | 🎯正反向运动学和动力学 | 🎯机器人刚体力学计算 | 🎯编辑参考系姿势和路径 | 🎯软件接口实体机器人模拟 | 🎯三角网格碰撞刚体模拟 | 🎯机器人比例微分积分控制、扭矩控制和速度控制模拟 | 🎯相机、激光传感器、陀螺仪、力/扭矩传感器和加速度计模拟 | 🎯集成ROS模拟 | 🎯运动规划器、约束流形上的运动规划 | 🎯快速轨迹优化 | 🎯实时运动规划 | 🎯解耦规划模型与模拟模型
📜刚体力学用例:Python自行车六自由度飞行器多连接件非线性运动方程模型


🍇Python力学动能势能
粒子 P 的线性动量定义为:
L P = m v L_P=m v LP=mv
其中 m m m是粒子 P P P的质量, v v v是粒子在惯性系中的速度。
类似地,刚体的线性动量定义为:
L B = m v ∗ L_B=m v ^* LB=mv∗
其中 m m m是刚体的质量, B B B, v ∗ v^* v∗是惯性系中 B B B质心的速度。
质点 P 绕惯性系 N 中任意点 O 的角动量定义为:
N H P / O = r × m v { }^N H ^{P / O}= r \times m v NHP/O=r×mv
其中 r r r是从点 O O O到质量 m m m的粒子的位置向量, v v v是惯性系中粒子的速度。
类似地,刚体 B 绕惯性系 N 中的点 O 的角动量定义为:
N H B / O = N H B / B ∗ + N H B ∗ / O { }^N H ^{B / O}={ }^N H ^{B / B^*}+{ }^N H ^{B^*} / O NHB/O=NHB/B∗+NHB∗/O
其中物体绕其质心的角动量为:
N H B / B ∗ = I ∗ ⋅ ω { }^N H ^{B / B^*}= I ^* \cdot \omega NHB/B∗=I∗⋅ω
质心关于 O 的角动量为:
N H B ∗ / O = r ∗ × m v ∗ { }^N H ^{B^*} / O= r ^* \times m v ^* NHB∗/O=r∗×mv∗
Python伪代码实现上述动量:
from pyx import symbols
from pyx.physics.mechanics import dynamicsymbols, ReferenceFrame
from pyx.physics.mechanics import RigidBody, Particle, Point, outer
from pyx.physics.mechanics import linear_momentum, angular_momentum
from pyx.physics.vector import init_vprinting
init_vprinting(pretty_print=False)
m, M, l1 = symbols('m M l1')
q1d = dynamicsymbols('q1d')
N = ReferenceFrame('N')
O = Point('O')
O.set_vel(N, 0 * N.x)
Ac = O.locatenew('Ac', l1 * N.x)
P = Ac.locatenew('P', l1 * N.x)
a = ReferenceFrame('a')
a.set_ang_vel(N, q1d * N.z)
Ac.v2pt_theory(O, N, a)
P.v2pt_theory(O, N, a)
最后,创建组成系统的主体。在这种情况下,系统由粒子 Pa 和刚体 A 组成。
Pa = Particle('Pa', P, m)
I = outer(N.z, N.z)
A = RigidBody('A', Ac, a, M, (I, Ac))
然后,人们可以选择评估系统各个组件的动量或整个系统本身的动量。
linear_momentum(N,A)
angular_momentum(O, N, Pa)
linear_momentum(N, A, Pa)
angular_momentum(O, N, A, Pa)
粒子 P 的动能定义为
T P = 1 2 m v 2 T_P=\frac{1}{2} m v ^2 TP=21mv2
其中 m m m是粒子 P P P的质量, v v v是粒子在惯性系中的速度。
类似地,刚体 B 的动能定义为
T B = T t + T τ T_B=T_t+T_\tau TB=Tt+Tτ
其中平动动能由下式给出:
T t = 1 2 m v ∗ ⋅ v ∗ T_t=\frac{1}{2} m v ^* \cdot v ^* Tt=21mv∗⋅v∗
旋转动能由下式给出:
T r = 1 2 ω ⋅ I ∗ ⋅ ω T_r=\frac{1}{2} \omega \cdot I ^* \cdot \omega Tr=21ω⋅I∗⋅ω
其中 m m m是刚体的质量, v ∗ v^* v∗是惯性系中质心的速度, ω \omega ω是刚体的惯性角速度, I ∗ I^* I∗是中心惯性二元。
势能定义为物体或系统因其位置或排列而拥有的能量。
物体或物体系统的拉格朗日定义为:
L = T − V L =T-V L=T−V
其中 T T T和 V V V分别是动能和势能。
Python伪代码实现:
from pyx import symbols
from pyx.physics.mechanics import dynamicsymbols, ReferenceFrame, outer
from pyx.physics.mechanics import RigidBody, Particle
from pyx.physics.mechanics import kinetic_energy, potential_energy, Point
from pyx.physics.vector import init_vprinting
init_vprinting(pretty_print=False)
m, M, l1, g, h, H = symbols('m M l1 g h H')
omega = dynamicsymbols('omega')
N = ReferenceFrame('N')
O = Point('O')
O.set_vel(N, 0 * N.x)
Ac = O.locatenew('Ac', l1 * N.x)
P = Ac.locatenew('P', l1 * N.x)
a = ReferenceFrame('a')
a.set_ang_vel(N, omega * N.z)
Ac.v2pt_theory(O, N, a)
P.v2pt_theory(O, N, a)
Pa = Particle('Pa', P, m)
I = outer(N.z, N.z)
A = RigidBody('A', Ac, a, M, (I, Ac))
然后,用户可以确定系统中任意数量实体的动能:
kinetic_energy(N, Pa)
kinetic_energy(N, Pa, A)
然后可以确定构成系统的任意数量的实体的势能:
Pa.potential_energy = m * g * h
A.potential_energy = M * g * H
potential_energy(A, Pa)
我们还可以确定该系统的拉格朗日量:
from pyx.physics.mechanics import Lagrangian
from pyx.physics.vector import init_vprinting
init_vprinting(pretty_print=False)
Lagrangian(N, Pa, A)
👉参阅更新:计算思维 | 亚图跨际
相关文章:

Python协作运动机器人刚体力学解耦模型
🎯要点 🎯腿式或固定式机器人模型 | 🎯网格、点云和体素网格碰撞检测 | 🎯正反向运动学和动力学 | 🎯机器人刚体力学计算 | 🎯编辑参考系姿势和路径 | 🎯软件接口实体机器人模拟 | Ἲ…...
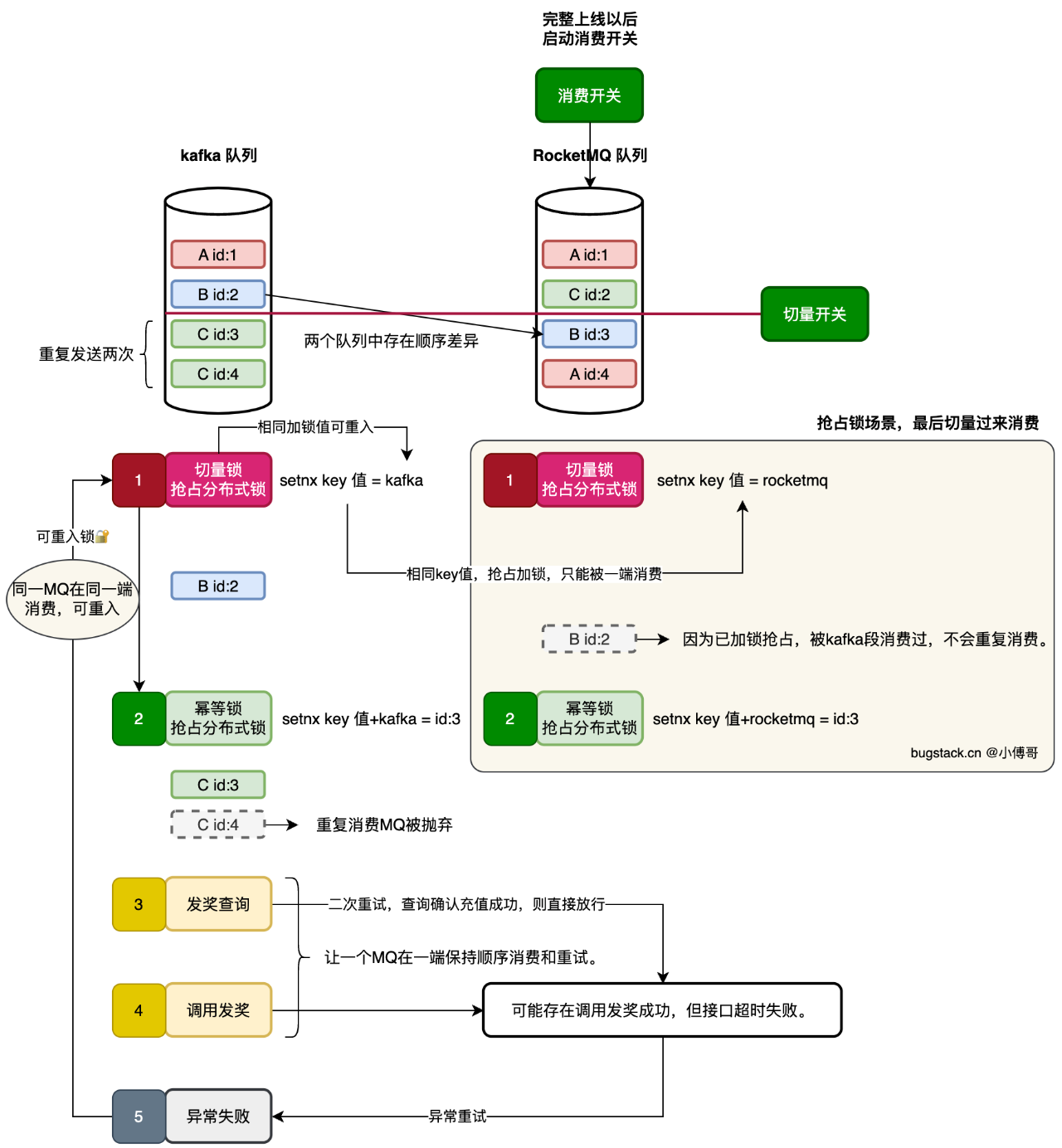
可重入锁思想,设计MQ迁移方案
如果你的MQ消息要从Kafka切换到RocketMQ且不停机,怎么做?在让这个MQ消息调用第三方发奖接口,但无幂等字段又怎么处理?今天小傅哥就给大家分享一个关于MQ消息在这样的场景中的处理手段。 这是一种比较特例的场景,需要保…...

Redis安装与使用
目录 1、介绍 1、redis的特点: 2、缓存 2、安装Redis 1、安装单机版redis 2、redis-cli命令参数 3、清空数据库的两种方式和作用域: 4、redis的增删查改命令 5、redis的查看所有分类命令 6、redis过期时间与控制键的行为 7、redis的相关工具 1、介绍 r…...

base64字符串空格问题
客户端使用的Content-Type为application/x-www-form-urlencoded时,字符串中出现了空格,base64解码时出错了,因为原来的字符有号, Spring Boot 对于Content-Type为application/x-www-form-urlencoded的HTTP请求,默认情…...

【BES2500x系列 -- RTX5操作系统】深入探索CMSIS-RTOS RTX -- 同步与通信篇 -- 消息队列和邮箱处理 --(四)
💌 所属专栏:【BES2500x系列】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! Ὁ…...
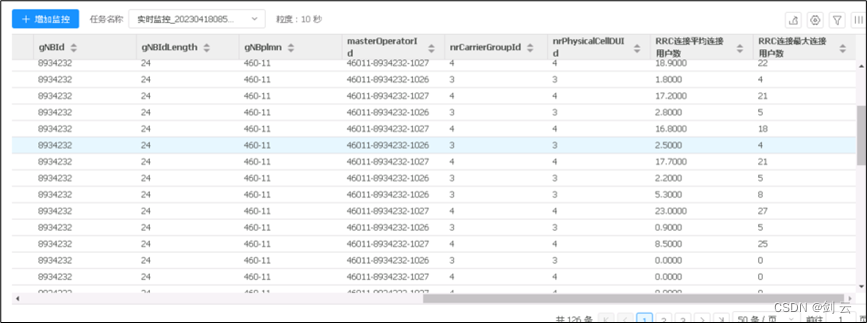
电信NR零流量小区处理
【摘要】随着目前网络建设逐步完善,5G用户的不断发展,针对零流量小区的分析及处理存在着必要性,零流量小区的出现既是用户分布及行为的直观体现,也是发展用户的一个指引,同时也能发现设备的一些故障。一个站点的能够带…...

ArcTs布局入门03——层叠布局(Stack)
如果你也对鸿蒙开发感兴趣,加入“Harmony自习室”吧! 扫描下面的二维码关注公众号。 1、概述 叠布局(StackLayout)用于在屏幕上预留一块区域来显示组件中的元素,提供元素可以重叠的布局。层叠布局通过Stack容器组件实…...
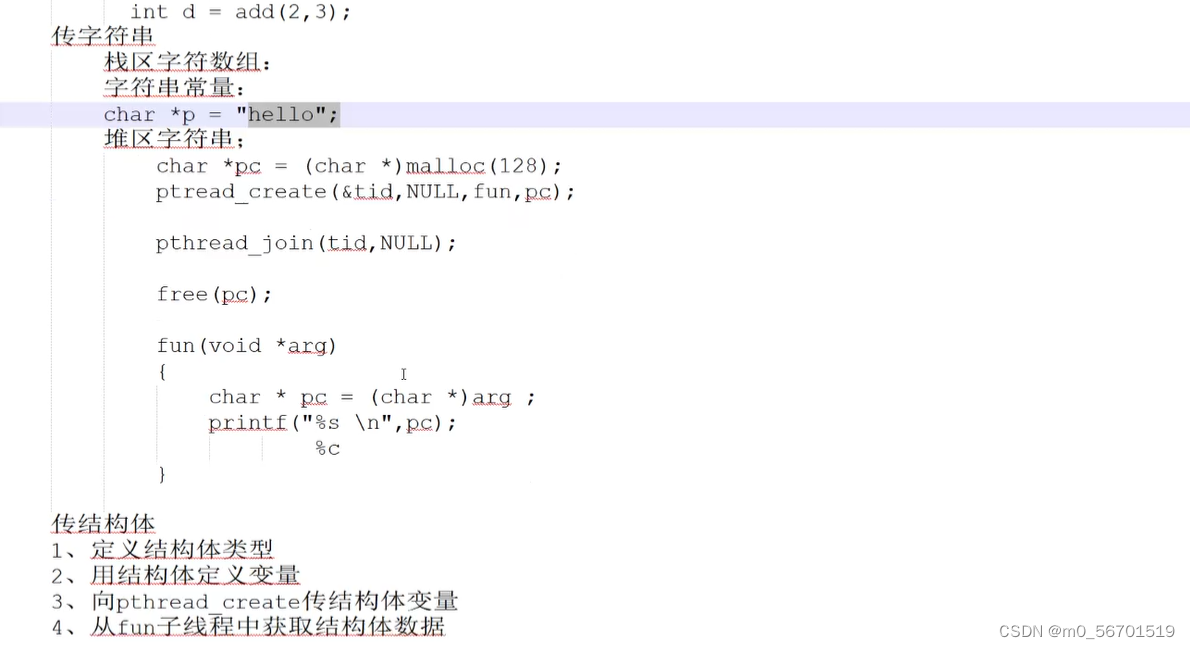
C语言之线程的学习
线程属于某一个进程 共同点:都能并发 线程共享变量,进程不共享。 多线程任务中,其中某一个线程调用了exit了,其他线程会跟着一起退出 如果是特定的线程就调用pthread_exit 失败返回的是错误号 下面也是...
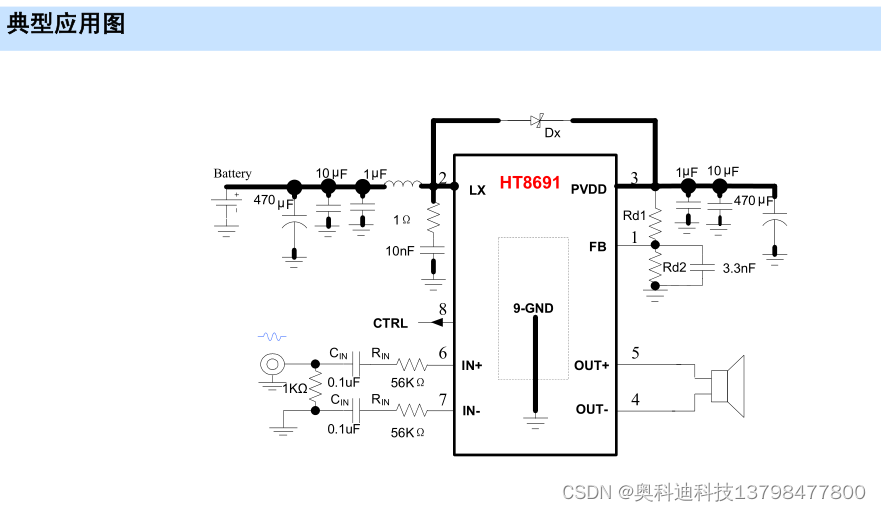
HT8691 内置升压模块的D类音频功率放大器芯片IC
一般描述 HT8691是一款内置升压模块的D类音频功率放大器。内置的升压模块可通过外置电阻调节升压值,即使是锂电池供电,在升压至6.5V时,10%THDN,4Ω负载条件下能连续输出5.5W功率;升压至7V,3Ω负载条件下则能连续输出7.0W功率。其支持外部设置…...

和小红书一起参会! 了解大模型与大数据融合的技术趋势
在过去的两年中,“大模型”无疑成为互联网行业的焦点话题,曾经炙手可热的大数据架构似乎淡出公众视野。然而,大数据领域并未停滞不前,反而快速演进,传统依赖众多开源组件的大数据平台正逐步过渡到以融合与简化为核心特…...
】7 Feeling)
【vocabulary in use (elementary)】7 Feeling
happy 高兴 sad 伤心 angry 生气 upset 丧气 cold 冷 hot 热 thirsty 口渴 hungry 饿 well 很好 ill 生病 tired 累了 surprised 惊讶 关于喜欢的表达: like to do 偶尔一次喜欢 like doing 一直喜欢的 outdoor activities 户外运动 be keep on doing 坚持做 be fo…...
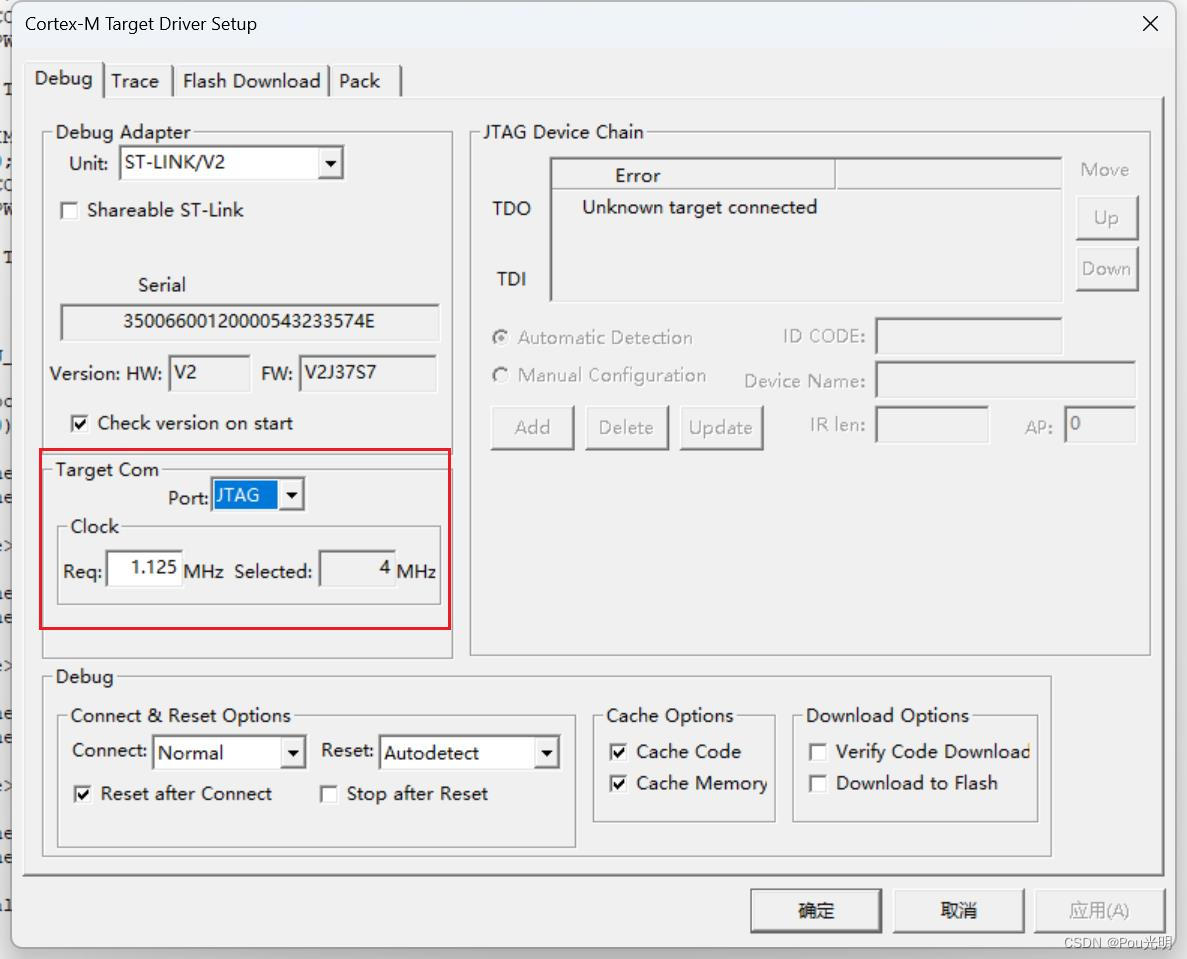
Keil5 ST-LINK setting闪退问题解决
1. 官网下载新版驱动文件 MDK uVision crashes when using ST-Link debugger 2. 解压替换 STLinkUSBDriver6.1.2.0Signed 我的库文件目录: D:\Tool\Keil5\ARM\STLink...

熟练掌握Docker及linux常用命令排查线上问题。熟悉Git, Maven等项目管理及构建工具,熟悉微服务中基于Jenkins的CI/CD
掌握Docker、Linux命令、项目管理及构建工具,以及CI/CD流程是现代软件开发和运维的关键技能。以下是对这些技能的概述和一些实践建议: ### Docker - **概述**:Docker是一个开源的容器化平台,允许开发者打包应用及其依赖到一个可移…...
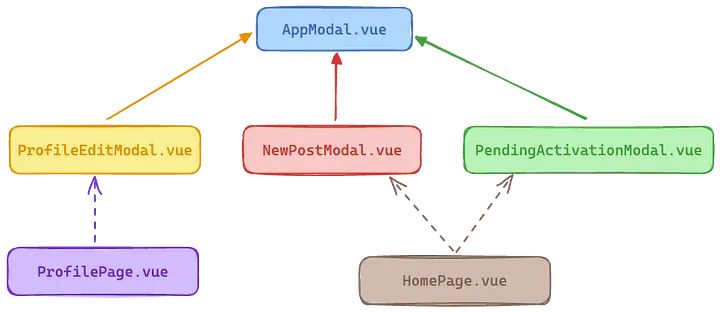
78.Vue 3 重用性模态框组件
模态框是大多数 Web 应用程序中的基本构建块。虽然最初实现起来可能看起来有点棘手,但实际上,使用 Vue 和一些 Flexbox 技巧,这不仅可行,而且非常简单。 让我们一起实现一个基础的模态框组件。 架构如下: AppModal.vue…...
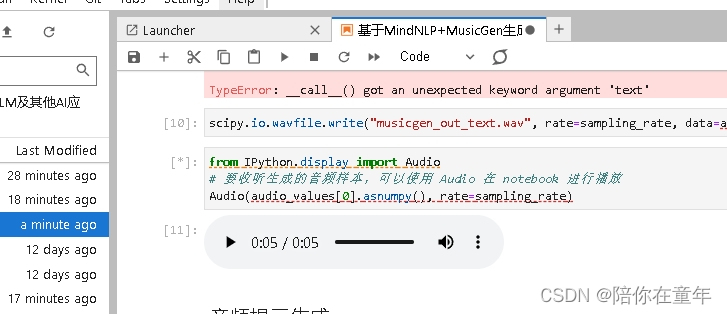
《昇思25天学习打卡营第9天|onereal》
继续学习昨天的 基于MindNLPMusicGen生成自己的个性化音乐 生成音乐 MusicGen支持两种生成模式:贪心(greedy)和采样(sampling)。在实际执行过程中,采样模式得到的结果要显著优于贪心模式。因此我们默认启…...

Wireshark - tshark支持iptables提供数据包
tshark现在的数据包获取方式有两种,分别是读文件、网口监听(af-packet原始套接字)。两种方式在包获取上,都是通过读文件的形式;存在文件io操作,在专门处理大流量的情境下, 我们复用wireshark去做…...

快团团团长如何批量退款可自定义退款金额(批量退差价)?
快团团团长如何批量退款可自定义退款金额(批量退差价)? 在售后处理中,经常会出现需要给某一商品退差价的场景,因此在批量退款时需要自定义退款金额。现快团团已支持批量退自定义金额,操作方法和注意事项如…...
MySQL——事务ACID原则、脏读、不可重复读、幻读
什么是事务 要么都成功,要么都失败 一一一一一一一 1. SQL执行:A给B转账 A 1000 ---->200 B 200 2. SQL执行:B收到A的钱 A 800 B 400 一一一一一一一 将一组SQL放在一个批次中去执行~ 事务原则:ACI…...

洗衣机水龙头要买有止逆阀的,多花几十元能省掉几万,值了
问大家一下,你家洗衣机水龙头用的是什么样的? 可能有业主会说我家买的是纯铜的,质量挺好的。 如果你家选的洗衣机水龙头仅仅是纯铜的,并没有其他的功能,你还是选做错了。 因为洗衣机水龙头…...

Android 蓝牙开发全面指南
Android 平台的蓝牙功能提供了丰富的API和工具,使开发者能够轻松实现从基本连接到复杂数据交换的各种蓝牙功能。蓝牙技术已经成为智能手机和其他设备间通信的重要方式,尤其在物联网和智能家居应用中有广泛应用。 关键词总结 Android 蓝牙开发涉及多个关…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
