ardupilot开发 --- 坐标变换 篇

Good Morning, and in case I don't see you, good afternoon, good evening, and good night!
- 0. 一些概念
- 1. 坐标系的旋转
- 1.1 轴角法
- 1.2 四元素
- 1.3 基于欧拉角的旋转矩阵
- 1.3.1 单轴旋转矩阵
- 1.3.2 多轴旋转矩阵
- 1.3.3 其他
- 2. 齐次变换矩阵
- 3. visp实践
0. 一些概念
- 相关概念:旋转矩阵、平移矩阵、单应矩阵、齐次变换矩阵。
- 坐标变换包括旋转变换和平移变换。
- 为什么要坐标变换?引入坐标变换可以解决哪些问题?应用场景?
- 已知一点p在坐标系A中的坐标,计算p在坐标系B中的坐标。
- 已知一向量v在坐标系A中的值,计算v在坐标系B中的值。
- 描述坐标系A和坐标系B之间的位姿关系(姿态和位置)。
- 一向量v绕坐标系A的xyz轴旋转 θ ϕ ψ \theta \phi \psi θϕψ角度并进行一定平移后在坐标系A中的新坐标。
- 在数学建模过程中,往往需要将不同的物量量表示在同一个坐标系内才能列出等式。
- 刚体运动学。
- 图像的投影。
1. 坐标系的旋转
描述坐标系的旋转常用的方法包括:
- 轴角法
- 旋转矩阵
- 欧拉角
- 四元数
这几种旋转表示方法有各自的优缺点和应用场景,这里不作赘叙。
1.1 轴角法
不常用,略…
1.2 四元素
待续…
1.3 基于欧拉角的旋转矩阵
轴角法和四元数,这两个可以归纳为用一次旋转来表示两个坐标系间的姿态。欧拉角则是用三次旋转来表示姿态。

欧拉角指:横滚角 ϕ \phi ϕ,俯仰角 θ \theta θ,偏航角 ψ \psi ψ。
ϕ , θ , ψ \phi, \theta, \psi ϕ,θ,ψ在不同的领域有不同的定义规则:主要的区别是旋转顺序的不同,绕原始(固定)坐标轴轴旋转还是绕新(运动)坐标轴的不同(也称外旋或内旋)。
在航天航空领域的欧拉角:
- 内旋
绕运动轴旋转得到新坐标系。 - Z–>Y–>X
原始坐标系经过Z–>Y–>X顺序旋转一定的角度得到新坐标系。 - 右手系
涉及的坐标系都遵循右手定则。
1.3.1 单轴旋转矩阵
前提:右手系
这里只给出结论,不作推导。
坐标系A分别单独绕 x , y , z x,y,z x,y,z轴旋转 ϕ , θ , ψ \phi, \theta, \psi ϕ,θ,ψ角度,欧拉旋转矩阵表达式如下:
T B A = R x ( ϕ ) = [ 1 0 0 0 c o s ϕ − s i n ϕ 0 s i n ϕ c o s ϕ ] (式 1 ) T B A = R y ( θ ) = [ c o s θ 0 s i n θ 0 1 0 − s i n θ 0 c o s θ ] (式 2 ) T B A = R z ( ψ ) = [ c o s ψ − s i n ψ 0 s i n ψ c o s ψ 0 0 0 1 ] (式 3 ) T_B^A=R_x(\phi)= \begin{bmatrix} 1&0&0\\ 0&cos{\phi}&-sin{\phi}\\ 0&sin{\phi}&cos{\phi} \end{bmatrix}(式1)\\[3mm] T_B^A=R_y(\theta)= \begin{bmatrix} cos{\theta}&0&sin{\theta}\\ 0&1&0\\ -sin{\theta}&0&cos{\theta} \end{bmatrix}(式2)\\[3mm] T_B^A=R_z(\psi)= \begin{bmatrix} cos{\psi}&-sin{\psi}&0\\ sin{\psi}&cos{\psi}&0\\ 0&0&1 \end{bmatrix}(式3) TBA=Rx(ϕ)= 1000cosϕsinϕ0−sinϕcosϕ (式1)TBA=Ry(θ)= cosθ0−sinθ010sinθ0cosθ (式2)TBA=Rz(ψ)= cosψsinψ0−sinψcosψ0001 (式3)
这些旋转矩阵的意义是:新坐标系到原始坐标系的变换矩阵,即:
[ x A y A z A ] = T B A [ x B y B z B ] \begin{bmatrix} x_A\\ y_A\\ z_A \end{bmatrix}=T_B^A \begin{bmatrix} x_B\\ y_B\\ z_B \end{bmatrix} xAyAzA =TBA xByBzB
注意:
- ϕ , θ , ψ \phi, \theta, \psi ϕ,θ,ψ满足右手定则,绕右手坐标系的正方向旋转时为正。
- ϕ , θ , ψ \phi, \theta, \psi ϕ,θ,ψ是系A旋转运动到系B的旋转量,但是得到的旋转矩阵 R x , R y , R z R_x,R_y,R_z Rx,Ry,Rz却是系B到系A的坐标变换矩阵!
即:
ϕ , θ , ψ \phi, \theta, \psi ϕ,θ,ψ:A ~> B
R x , R y , R z R_x,R_y,R_z Rx,Ry,Rz:B ~> A - 系B到系A的变换矩阵可以有多种符号表示方式,通常有:
T B A T_B^A TBA
A T B ^AT_B ATB
T A B T_{AB} TAB
都表示 B ~> A 的变换关系矩阵!注意上下标的位置!! - 旋转矩阵是正交的,因此有:
[ x B y B z B ] = T A B [ x A y A z A ] = ( T B A ) − 1 [ x A y A z A ] = ( T B A ) T [ x A y A z A ] \begin{bmatrix} x_B\\ y_B\\ z_B \end{bmatrix}=T_A^B \begin{bmatrix} x_A\\ y_A\\ z_A \end{bmatrix}=(T_B^A)^{-1} \begin{bmatrix} x_A\\ y_A\\ z_A \end{bmatrix}=(T_B^A)^{T} \begin{bmatrix} x_A\\ y_A\\ z_A \end{bmatrix} xByBzB =TAB xAyAzA =(TBA)−1 xAyAzA =(TBA)T xAyAzA
即: T A B = ( T B A ) − 1 = ( T B A ) T T_A^B=(T_B^A)^{-1}=(T_B^A)^{T} TAB=(TBA)−1=(TBA)T.
1.3.2 多轴旋转矩阵
12种常用的内旋欧拉角又可分为两个类别:
- 常规欧拉角
- 泰特 - 布赖恩角
注意: 下表中如 X 1 Y 2 Z 3 X_1Y_2Z_3 X1Y2Z3表示的是矩阵相乘顺序,相当于本文的 R x R y R z R_xR_yR_z RxRyRz,表示旋转顺序是 Z ~>Y ~>X !其中的123表示绕该轴旋转的角度代称!

在航空航天领域,常用 Z ~>Y ~>X 旋转顺序的内旋欧拉角旋转矩阵。
例如,系A分别先后绕 Z , Y , X Z,Y,X Z,Y,X轴旋转 ψ , θ , ϕ \psi,\theta,\phi ψ,θ,ϕ角度,得到新的坐标系B,则有以下等式成立:
[ x A y A z A ] = T B A [ x B y B z B ] T B A = R x ( ϕ ) R y ( θ ) R z ( ψ ) = [ c o s θ c o s ψ − c o s θ s i n ψ s i n θ c o s ϕ s i n ψ + c o s ψ s i n ϕ s i n θ c o s ϕ c o s ψ − s i n ϕ s i n θ s i n ψ − c o s θ s i n ϕ s i n ϕ s i n ψ − c o s ϕ c o s ψ s i n θ c o s ψ s i n ϕ + c o s ϕ s i n θ s i n ψ c o s ϕ c o s θ ] (式 4 ) 首旋:绕系 A 的 Z 轴旋转 ψ 角度 次旋:绕首旋得到的坐标系 A ′ 的 Y 轴旋转 θ 角度 终旋:绕次旋得到的坐标系 A ′ ′ 的 X 轴旋转 ϕ 角度 系 A → 首旋 → 系 A ′ → 次旋 → 系 A ′ ′ → 终旋 → 系 B \begin{bmatrix} x_A\\ y_A\\ z_A \end{bmatrix}=T_B^A \begin{bmatrix} x_B\\ y_B\\ z_B \end{bmatrix} \\[5mm] T_B^A=R_x(\phi)R_y(\theta)R_z(\psi)=\begin{bmatrix} cos{\theta}cos{\psi}&-cos{\theta}sin{\psi}&sin{\theta}\\ cos{\phi}sin{\psi}+cos{\psi}sin{\phi}sin{\theta}&cos{\phi}cos{\psi}-sin{\phi}sin{\theta}sin{\psi}&-cos{\theta}sin{\phi}\\ sin{\phi}sin{\psi}-cos{\phi}cos{\psi}sin{\theta}&cos{\psi}sin{\phi}+cos{\phi}sin{\theta}sin{\psi}&cos{\phi}cos{\theta} \end{bmatrix}(式4)\\[5mm] 首旋:绕系A的Z轴旋转\psi角度\\[5mm] 次旋:绕首旋得到的坐标系A'的Y轴旋转\theta角度\\[5mm] 终旋:绕次旋得到的坐标系A''的X轴旋转\phi角度\\[5mm] 系A\to 首旋 \to 系A' \to 次旋 \to 系A'' \to 终旋 \to 系B xAyAzA =TBA xByBzB TBA=Rx(ϕ)Ry(θ)Rz(ψ)= cosθcosψcosϕsinψ+cosψsinϕsinθsinϕsinψ−cosϕcosψsinθ−cosθsinψcosϕcosψ−sinϕsinθsinψcosψsinϕ+cosϕsinθsinψsinθ−cosθsinϕcosϕcosθ (式4)首旋:绕系A的Z轴旋转ψ角度次旋:绕首旋得到的坐标系A′的Y轴旋转θ角度终旋:绕次旋得到的坐标系A′′的X轴旋转ϕ角度系A→首旋→系A′→次旋→系A′′→终旋→系B
旋转矩阵是正交的,因此有:
T A B = ( T B A ) − 1 = ( T B A ) T T_A^B=(T_B^A)^{-1}=(T_B^A)^{T} TAB=(TBA)−1=(TBA)T
实质上,可以自行根据(式1)(式2)(式3)进行不同顺序的相乘,以得到特定的欧拉旋转矩阵,(式4)就是下面相乘顺序得到的结果:
T B A = R x ( ϕ ) R y ( θ ) R z ( ψ ) T_B^A=R_x(\phi)R_y(\theta)R_z(\psi) TBA=Rx(ϕ)Ry(θ)Rz(ψ)
注意,越靠右边旋转顺序越优先!!
1.3.3 其他
- 优点:简洁直观。
- 缺点:万向节死锁,意思是在某些姿态下,欧拉角的三自由度失去了一个自由度。
- 扩展结论:
- 欧拉角旋转矩阵是正交的,有 R T = R − 1 R^T=R^{-1} RT=R−1
- 三次绕固定轴旋转的最终姿态和以相反顺序三次绕运动轴旋转的最终姿态相同。
- 欧拉角+旋转矩阵才能 VS 轴角法+四元数
- 外旋欧拉旋转矩阵请自行查阅其他资料。
2. 齐次变换矩阵
将两个坐标系的旋转关系和平移关系整合成一个4x4的矩阵。
[ x b y b z b 1 ] = b T a [ x a y a z a 1 ] = [ b R a O a b 0 1 ] [ x a y a z a 1 ] \begin{bmatrix} x_b \\ y_b \\ z_b \\ 1 \end{bmatrix}={^bT_a} \begin{bmatrix} x_a \\ y_a \\ z_a \\ 1 \end{bmatrix}= \begin{bmatrix} ^bR_a&O_a^b \\ 0&1 \\ \end{bmatrix} \begin{bmatrix} x_a \\ y_a \\ z_a \\ 1 \end{bmatrix} xbybzb1 =bTa xayaza1 =[bRa0Oab1] xayaza1
b T a = [ b R a O a b 0 1 ] {^bT_a} = \begin{bmatrix} ^bR_a&O_a^b \\ 0&1 \\ \end{bmatrix} bTa=[bRa0Oab1]
其中:
b T a ^bT_a bTa称为坐标系 a 到坐标系 b 的齐次变换矩阵;
b R a ^bR_a bRa是系a到系b的旋转矩阵;
O a b O_a^b Oab是系a原点在系b中的坐标;
坐标系 a 到坐标系 b 的齐次变换矩阵为 b T a ^bT_a bTa,那么坐标系 b 到坐标系 a 的齐次变换矩阵为 a T b = ( b T a ) − 1 ^aT_b=(^bT_a)^{-1} aTb=(bTa)−1,根据齐次矩阵的性质,可知:
a T b = ( b T a ) − 1 = [ a R b − a R b O a b 0 1 ] ^aT_b=(^bT_a)^{-1}= \begin{bmatrix} ^aR_b&-^aR_bO_a^b \\ 0&1 \\ \end{bmatrix} aTb=(bTa)−1=[aRb0−aRbOab1]
3. visp实践
//! [compute cMe]
vpRxyzVector c1TOc_xyz(vpMath::rad(-10.0), vpMath::rad(0), 0); // c1 ~> c 的xyz轴旋转量 !
vpRotationMatrix c1Rc(c1TOc_xyz); // 旋转矩阵:c -> c1
vpRotationMatrix cRc1 = c1Rc.inverse(); // 旋转矩阵:c1 -> c, 旋转矩阵是正交的,因此 c1Rc^-1==c1Rc^T
vpHomogeneousMatrix cMc1(vpTranslationVector(), cRc1); // 齐次变换矩阵:c1 -> c
vpRotationMatrix c1Re { 1, 0, 0, 0, 0, 1, 0, -1, 0 }; // 旋转矩阵:e -> c1 !
vpTranslationVector e0_c1(0, -0.03, -0.07); // 平移关系:e系原点在c1系中的坐标 !
vpHomogeneousMatrix c1Me(e0_c1, c1Re); // 齐次变换矩阵:e -> c1
vpHomogeneousMatrix cMe = cMc1 * c1Me; // 齐次变换矩阵:e -> c
vpVelocityTwistMatrix cVe(cMe); // 伺服系统控制量Vc=[vx,vy,vz,wx,wy,wz]的坐标变换矩阵:e -> c,从飞机机体系FRD到相机系RDF
//! [compute cMe]
相关文章:

ardupilot开发 --- 坐标变换 篇
Good Morning, and in case I dont see you, good afternoon, good evening, and good night! 0. 一些概念1. 坐标系的旋转1.1 轴角法1.2 四元素1.3 基于欧拉角的旋转矩阵1.3.1 单轴旋转矩阵1.3.2 多轴旋转矩阵1.3.3 其他 2. 齐次变换矩阵3. visp实践 0. 一些概念 相关概念&am…...

git clone 别人项目后正确的修改和同步操作
简介 git clone主要是克隆别人的开源项目。但更高端的操作是实现本地修改的同时,能同步别人的在线修改,并且不相互干扰: 克隆原始项目:从远程仓库克隆项目到本地。添加上游仓库:将原始项目的远程仓库添加为上游仓库。…...
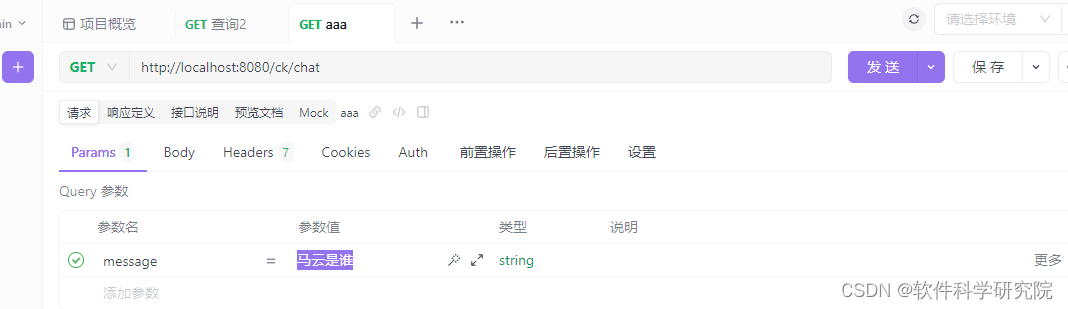
JAVA连接FastGPT实现流式请求SSE效果
FastGPT 是一个基于 LLM 大语言模型的知识库问答系统,提供开箱即用的数据处理、模型调用等能力。同时可以通过 Flow 可视化进行工作流编排,从而实现复杂的问答场景! 一、先看效果 真正实流式请求,SSE效果,SSE解释&am…...

二分查找1
1. 二分查找(704) 题目描述: 算法原理: 暴力解法就是遍历数组来找到相应的元素,使用二分查找的解法就是每次在数组中选定一个元素来将数组划分为两部分,然后因为数组有序,所以通过大小关系舍弃…...
什么美业门店管理系统好用?2024美业收银系统软件排名分享
美业SAAS系统在美容、美发、美甲等行业中十分重要,这种系统为美业提供了一种数字化解决方案,帮助企业更高效地管理业务和客户关系。 美业门店管理系统通常提供预约管理、客户管理、库存管理、报表生成等一系列功能,以满足美容院、美发沙龙等…...

【文件上传】
文件上传漏洞 FileUpload 0x01 定义 服务端未对客户端上传文件进行严格的 验证和过滤造成可上传任意文件情况;0x02 攻击满足条件: 1. 上传文件能够被Web容器解释执行 2. 找到文件位置 3.上传文件未被改变内容。(躲避安全检查&#…...

Golang 单引号、双引号和反引号的概念、用法以及区别
在 Golang(Go 语言)中,单引号 ()、双引号 (") 和反引号 () 用于不同类型的字符串和字符表示。以下是它们的概念、用法和区别: 1. 单引号 () 概念 单引号用于表示 字符(rune 类型)。一个字符表示一个…...
linux和mysql基础指令
Linux中nano和vim读可以打开记事文件。 ifdown ens33 ifup ens33 关闭,开启网络 rm -r lesson1 gcc -o code1 code1.c 编译c语言代码 ./code1 执行c语言代码 rm -r dir 删除文件夹 mysql> show databases-> ^C mysql> show databases; -------…...

JDK 为什么需要配置环境变量
前言 首先,我们要知道 Java 程序的执行过程。首先将 xxx.java 文件(使用 javac 编译指令)编译成 xxx.class 文件(字节码文件),再将字节码文件(使用 java 执行指令)解释成电脑所能认识…...
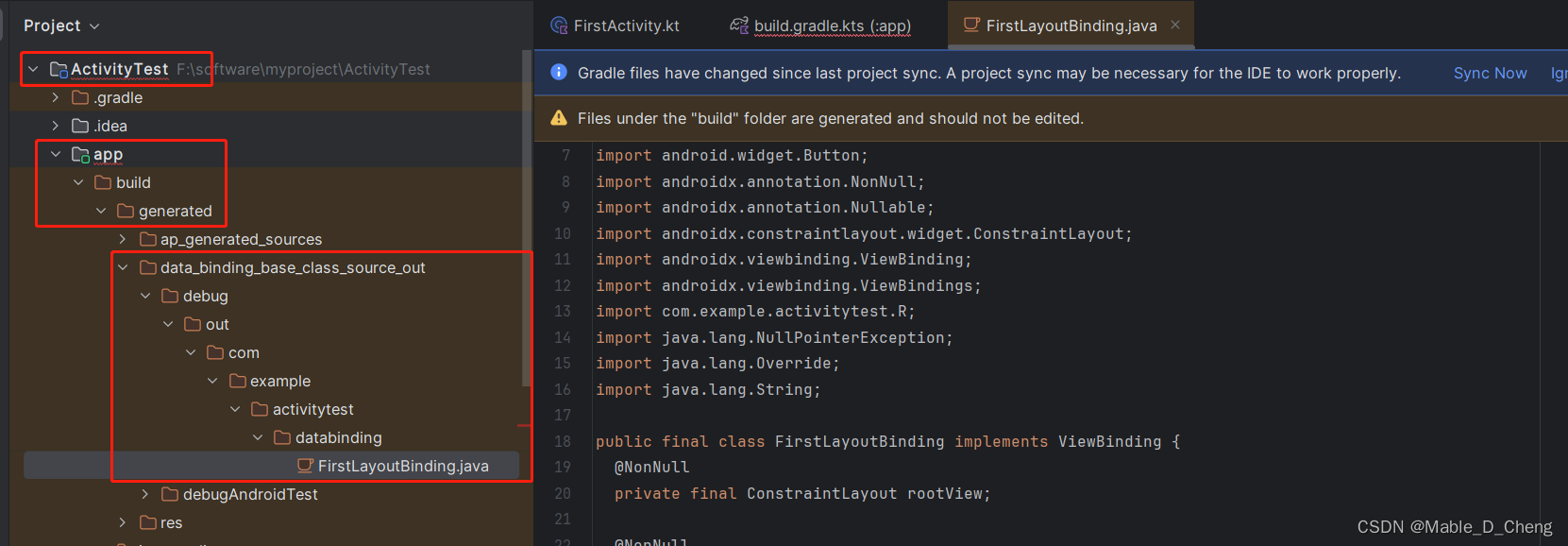
ViewBinding的使用(因为kotlin-android-extensions插件的淘汰)
书籍: 《第一行代码 Android》第三版 开发环境: Android Studio Jellyfish | 2023.3.1 问题: 3.2.4在Activity中使用Toast章节中使用到了kotlin-android-extensions插件,但是该插件已经淘汰,根据网上了解,目前使用了新的技术VewBinding替…...

IOS Swift 从入门到精通:ios 连接数据库 安装 Firebase 和 Firestore
创建 Firebase 项目 导航到Firebase 控制台并创建一个新项目。为项目指定任意名称。 在这里插入图片描述 下一步,启用 Google Analytics,因为我们稍后会用到它来发送推送通知。 在这里插入图片描述 在下一个屏幕上,选择您的 Google Analytics 帐户(如果已创建)。如果没…...

QT4-QT5(6)-const char* QString 乱码转换
我简单粗暴的给出个结论: QString GBK编码正常,可以转UTF-8编码,但会有少量乱码。 const char* 编码就不要转编码,转哪个都是乱码。 UTF-8.cpp 下 1.QString GBK->UTF-8 2.const char * GBK->UTF-8 const char *…...

报错:RuntimeError_ cuDNN error_ CUDNN_STATUS_EXECUTION_FAILED
原因:pytorch与cuda版本不对 也有可能是内存空间不足,可以更改虚拟空间大小,参考:解决电脑内存不足问题:Win10虚拟内存设置指南...

黑马点评项目总结1-使用Session发送验证码和登录login和 使用Redis存储验证码和Redis的token登录
黑马先是总结了从session实现登录,然后是因为如果使用了集群方式的服务器的话,存在集群共享session互相拷贝效率低下的问题,接着引出了速度更快的内存型的kv数据库Redis, 使用Session发送验证码和登录login 举个例子:…...

【大模型】Vllm基础学习
前言:vllm是一个大语言模型高速推理框架,旨在提高大模型的服务效率。优势是内存管理,实现的核心是pageattetion算法。仅在gpu上加速,不在cpu加速。 目录 1. PageAttention2. 实践2.1 安装2.2 离线推理2.3 适配OpenAI的api 1. Page…...

使用vue动态给同一个a标签添加内容 并给a标签设置hover,悬浮文字变色,结果鼠标悬浮有的字上面不变色
如果Vue的虚拟DOM更新机制导致样式更新不及时,你可以尝试以下几种方法来解决这个问题: 确保使用响应式数据: 确保你使用的数据是响应式的,并且任何对这些数据的更改都会触发视图的更新。在Vue中,你应该使用data对象中的…...

【ajax实战06】进行文章发布
本文章目标:收集文章内容,并提交服务器保存 一:基于form-serialize插件收集表单数据 form-serialize插件仅能收集到表单数据,除此之外的数据无法收集到 二:基于axios提交到服务器保存 三:调用alert警告…...
Codeforces Round 954 (Div. 3)(A~E)
目录 A. X Axis B. Matrix Stabilization C. Update Queries D. Mathematical Problem A. X Axis Problem - A - Codeforces 直接找到第二大的数,答案就是这个数与其他两个数的差值的和。 void solve() {vector<ll>a;for (int i 1; i < 3; i){int x;…...
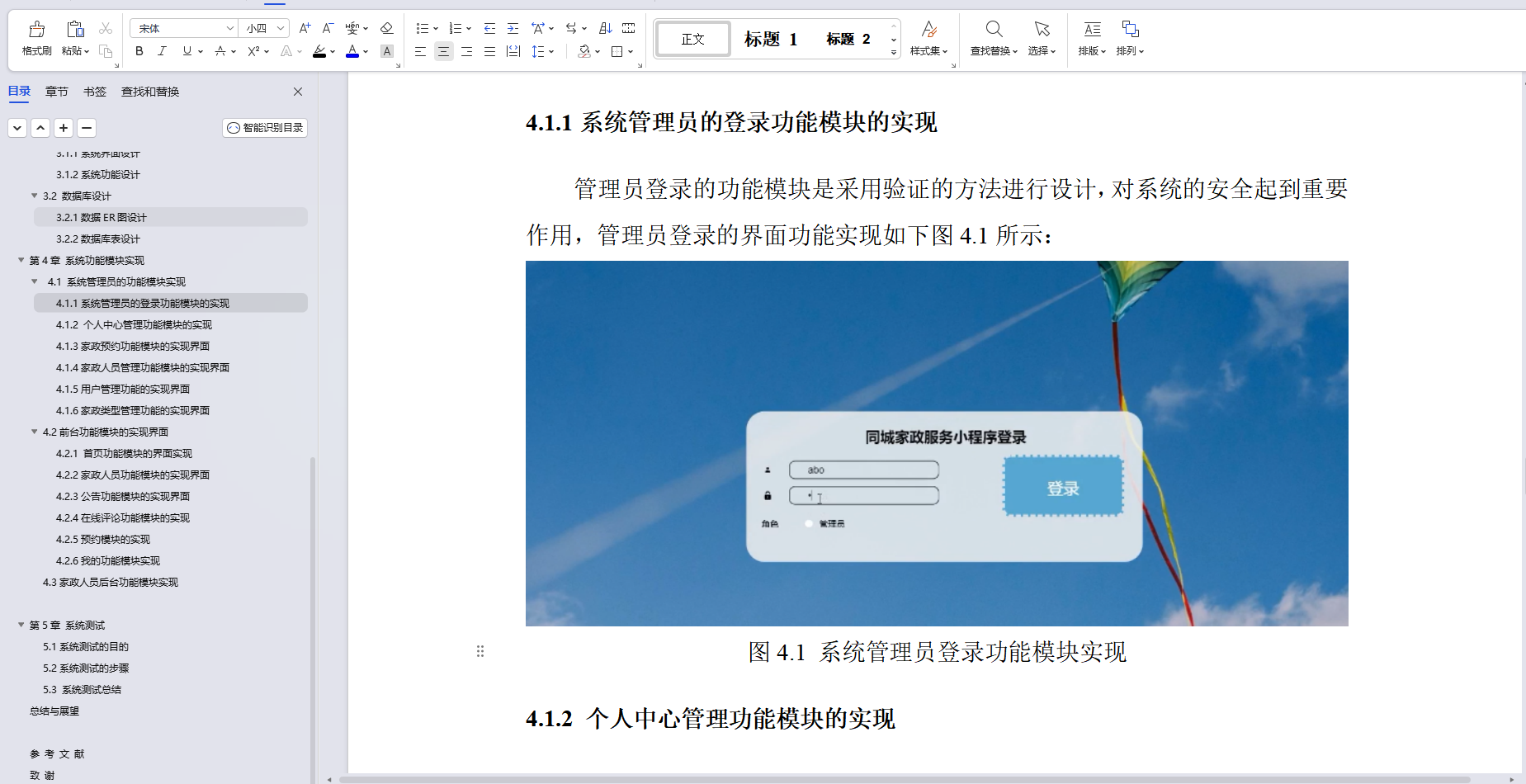
基于Java微信小程序同城家政服务系统设计和实现(源码+LW+调试文档+讲解等)
💗博主介绍:✌全网粉丝10W,CSDN作者、博客专家、全栈领域优质创作者,博客之星、平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 🌟文末获取源码数据库🌟感兴趣的可以先收藏起来,还…...
[21] Opencv_CUDA应用之使用Haar级联的对象检测
Opencv_CUDA应用之使用Haar级联的对象检测 Haar级联使用矩形特征来检测对象,它使用不同大小的矩形来计算不同的线和边缘特征。矩形包含一些黑色和白色区域,如下图所示,它们在图像的不同位置居中 类Haar特征检测算法的思想是计算矩形内白色像素和黑色像素之间的差异这个方法的…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...

若依项目部署--传统架构--未完待续
若依项目介绍 项目源码获取 #Git工具下载 dnf -y install git #若依项目获取 git clone https://gitee.com/y_project/RuoYi-Vue.git项目背景 随着企业信息化需求的增加,传统开发模式存在效率低,重复劳动多等问题。若依项目通过整合主流技术框架&…...

C++ Saucer 编写Windows桌面应用
文章目录 一、背景二、Saucer 简介核心特性典型应用场景 三、生成自己的项目四、以Win32项目方式构建Win32项目禁用最大化按钮 五、总结 一、背景 使用Saucer框架,开发Windows桌面应用,把一个html页面作为GUI设计放到Saucer里,隐藏掉运行时弹…...
