第二证券:可转债基础知识?想玩可转债一定要搞懂的交易规则!
可转债,全称是“可转化公司债券”,是上市公司为了融资,向社会公众所发行的一种债券,具有股票和债券的双重特点,投资者可以选择按照发行时约定的价格将债券转化成公司一般股票,也可作为债券持有到期后收取本息或在提前在市场流转变现。
一般状况下可转债的闭锁期(即不能转股期)为该转债发行日起的6个月内,不过具体还要看相关文件和公告的规定。
一般公司发行的可转债最短1年,最长6年,发行到期后可转债会退市,公司会换回一切的可转债,支交给投资者本金与利息。只需投资者手中还持有可转债,那么可转债到期后无需进行任何操作,系统会根据账户的持有状况,将兑付的本金和利息主动划转到账户中。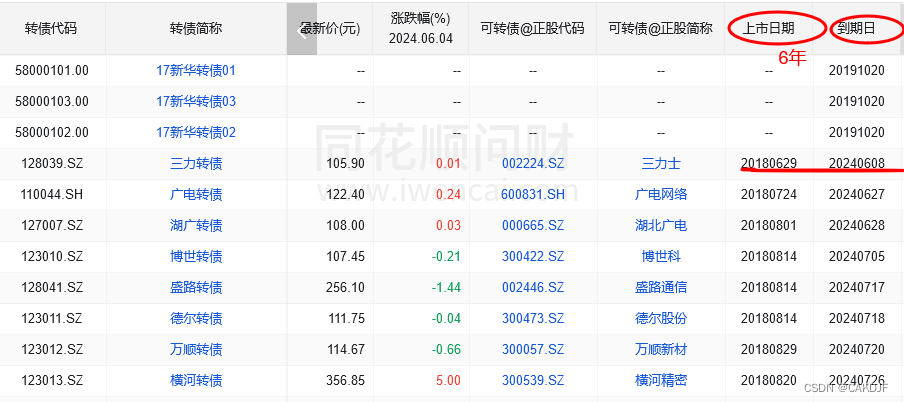
可转债买卖规则
1、买卖时刻:买卖日的9:30-11:30,13:00-15:00。
2、可转债是t+0买卖,当天买入后当天就可以卖出,并且不限次数。
3、可转债最小单位为1手,每次买入有必要是1手的整数倍,在卖出时,缺乏1手的部分,应当一次性卖出,其间1手一般为10张。
4、可转债涨跌幅限制:
上市首日涨幅限制为57.3%,跌幅限制为43.3%,除上市首日外,可转债的价格涨跌幅限制份额为20%。盘中设有暂时停牌机制,规则如下:
盘中成交价较前收盘价初次上涨或跌落到达或超越20%的,暂时停牌时刻为30分钟;
盘中成交价较前收盘价初次上涨或跌落到达或超越30%的,暂时停牌至14:57,暂时停牌时刻跨越14:57的,于当日14:57复牌。
5、注册可转债买卖权限
两年的股票买卖经历,从第一笔股票买卖的时刻开端计算;
注册权限前20个买卖日,证券账户内有10万元以上的日均资产,资产包含现金,股票,国债逆回购,基金等。如果有20万,只需要10个买卖日。
6、强制换回
正股价接连15-20天高于转股价的130%,公司将以103元的价格换回。
正股价持续约30天低于转股价的70%-80%,公司有必要以101-103的价格来换回。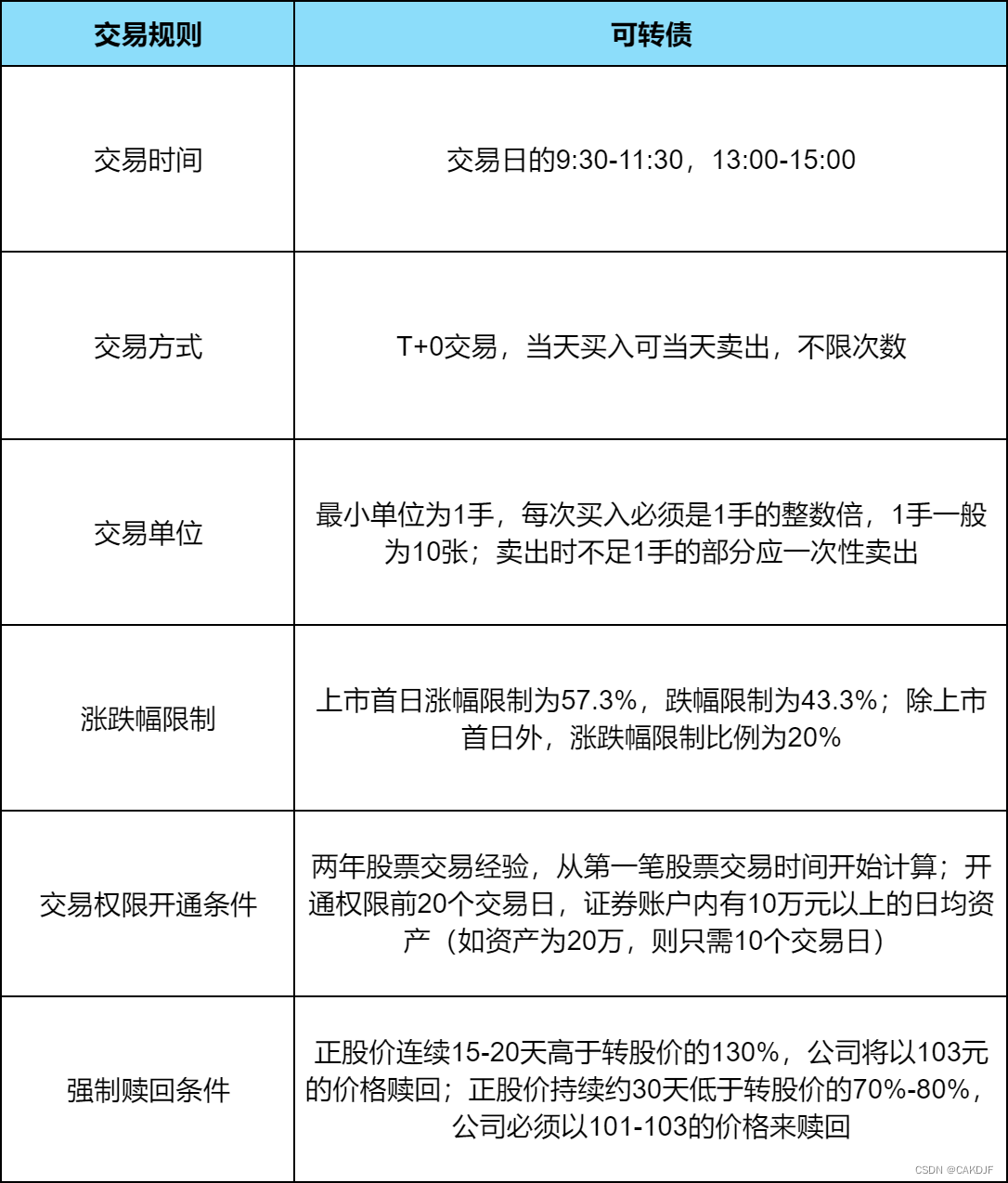
注:可转债集合竞价
1、成交量最大原则
即某一个价格买入单和卖出单能同时成交的量最大,则开盘价便是它。
2、竞价时刻:
早盘集合竞价:买卖日的9:15-9:25,9:15-9:20可挂单、可撤单,9:20-9:25可挂单、不可撤单。
尾盘集合竞价:买卖日的14:57-15:00,深交所可转债是集合竞价,可挂单不可撤单。(上交所可转债是接连竞价,可挂单可撤单。)
3、竞价规模:
沪市:不超越前收盘价的70%~150%,比如上市首日开盘价格规模为70元~150元。
深市:上市首日开盘集合竞价规模为发行价的±30%,也是就开盘价格规模为70元~130元;非上市首日开盘集合竞价规模为前收盘价的±10%;此外复盘集合竞价、收盘集合竞价规模为最近成交价的±10%。
沪市可转债如果申报价格超出有用竞价规模,视为废单。而深市则是保存起来,价格触发后可成交。
以上便是关于“可转债基础知识?想玩可转债一定要搞懂的买卖规则”的知识
相关文章:

第二证券:可转债基础知识?想玩可转债一定要搞懂的交易规则!
可转债,全称是“可转化公司债券”,是上市公司为了融资,向社会公众所发行的一种债券,具有股票和债券的双重特点,投资者可以选择按照发行时约定的价格将债券转化成公司一般股票,也可作为债券持有到期后收取本…...

原型模式的实现
1. 引言 1.1 背景 在实际编程中,有时需要频繁创建多个相似但稍有不同的对象。如果采用传统的对象创建方式,容易造成代码冗余,对象重复初始化操作也可能带来大量的的资源消耗(如时间、内存等)。这样不仅降低了灵活性,导致难以适应状态的变化,还降低了代码的可扩展性。 …...

【第二套】华为 2024 年校招-硬件电源岗
1.为了避免 50Hz 的电⽹电压⼲扰放⼤器,应该⽤那种滤波器: A.带阻滤波器 B.带通滤波器 C.低通滤波器 D.⾼通滤波器 2.PID 中的 I 和 D 的作⽤分别是? A、消除静态误差和提⾼动态性能 B、消除静态误差和减⼩调节时间 C、提⾼动态性能和减⼩超调…...
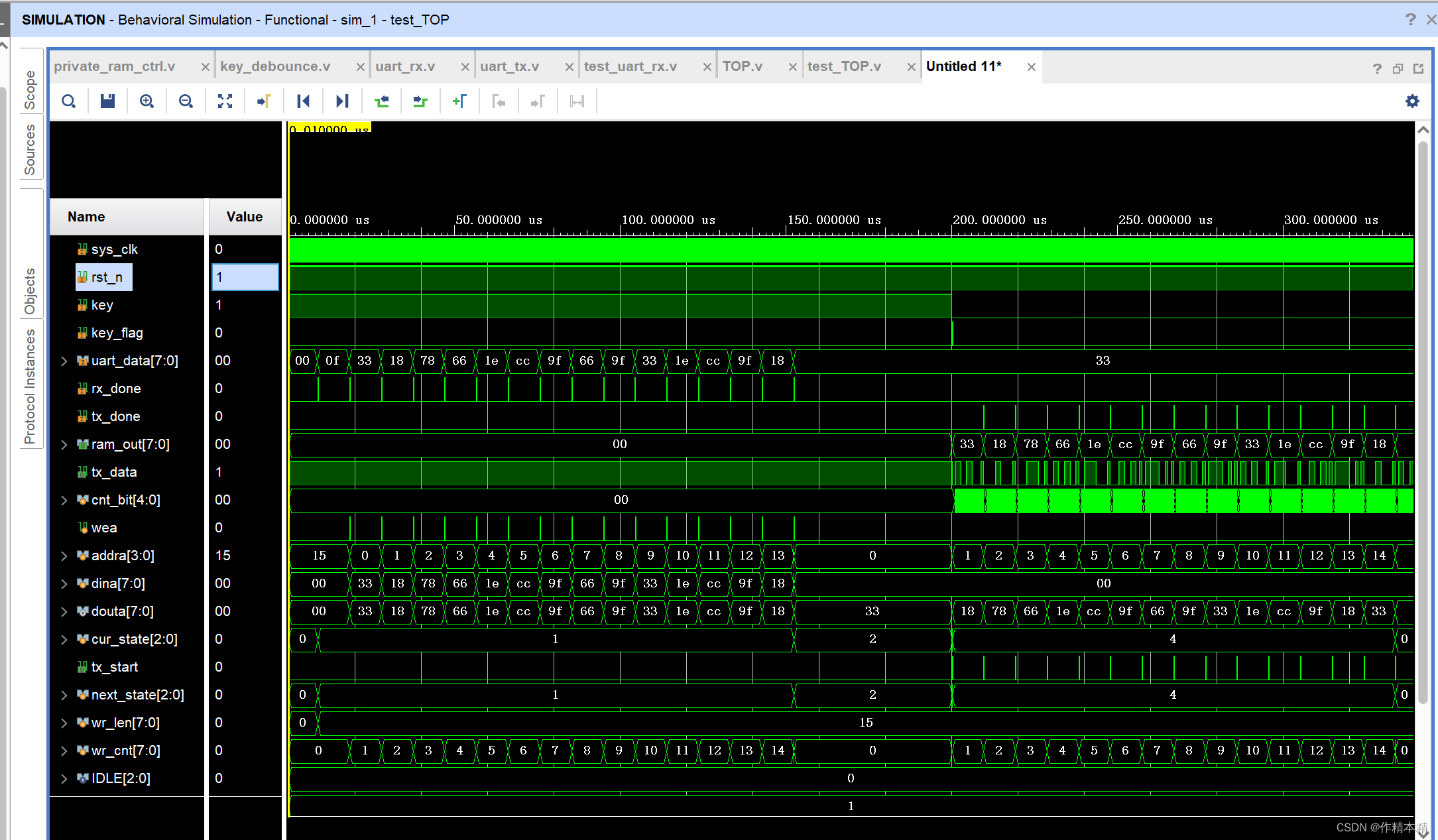
Xilinx FPGA:vivado利用单端RAM/串口传输数据实现自定义私有协议
一、项目要求 实现自定义私有协议,如:pc端产生数据:02 56 38 ,“02”代表要发送数据的个数,“56”“38”需要写进RAM中。当按键信号到来时,将“56”“38”读出返回给PC端。 二、信号流向图 三、状态…...

Spark on k8s 源码解析执行流程
Spark on k8s 源码解析执行流程 1.通过spark-submit脚本提交spark程序 在spark-submit脚本里面执行了SparkSubmit类的main方法 2.运行SparkSubmit类的main方法,解析spark参数,调用submit方法 3.在submit方法里调用doRunMain方法,最终调用r…...

粤港联动,北斗高质量国际化发展的重要机遇
今年是香港回归27周年,也是《粤港澳大湾区发展规划纲要》公布5周年,5年来各项政策、平台不断为粤港联动增添新动能。“十四五”时期的粤港澳大湾区,被国家赋予了更重大的使命,国家“十四五”《规划纲要》提出,以京津冀…...

Chrome导出cookie的实战教程
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...

视频文字转语音经验笔记
自媒体视频制作的一些小经验,分享给大家。 一、音频部分: 1、文字转语音阐述: 微软语音识别 云希-青年男, 0.5-0.8变速 。注:云泽-中年男(不支持长音频录制), 适合郑重场合&#…...

视频融合共享平台LntonCVS统一视频接入平台智慧安防应用方案
安防视频监控平台LntonCVS是一款拥有强大拓展性和灵活部署能力的综合管理平台。它支持多种主流标准协议,包括国标GB28181、RTSP/Onvif、RTMP等,同时兼容各厂家的私有协议和SDK,如海康Ehome、海大宇等。LntonCVS不仅具备传统安防视频监控功能&…...

使用Python绘制动态螺旋线:旋转动画效果
文章目录 引言准备工作前置条件 代码实现与解析导入必要的库初始化Pygame绘制螺旋线函数主循环 完整代码 引言 螺旋线是一个具有美学和数学魅力的图形。通过编程,我们可以轻松创建动态旋转的螺旋线动画。在这篇博客中,我们将使用Python和Pygame库来实现…...

Symfony实战手册:PHP框架的高级应用技巧
引言 Symfony是一个功能强大且广泛应用于PHP应用程序开发的框架,它提供了许多高级特性和工具,可以帮助开发人员更高效地构建和管理复杂的Web应用程序。以下是Symfony框架的几个关键方面及其高级应用技巧: 1. 路由和控制器 Symfony的路由组…...
TOGAF培训什么内容?参加TOGAF培训有什么好处?考试通过率多少?
TOGAF培训什么内容?参加TOGAF培训有什么好处?考试通过率多少? TOGAF培训哪些内容? 通过本课程,你将掌握TOGAF的理论和实践,理解企业架构的影响,能够评估、启动、设 计、执行新一轮企业和IT架构…...

keepalived HA nginx方案
安装 centos: yum -y install epel-release yum -y install nginx keepalivedkeepalived配置解析 /etc/keepalived/keepalived.conf ! Configuration File for keepalived # 全局变量 global_defs {router_id nginx_ha # 主从保持一致script_user root # 执行健康检查的…...
 known to git)
报错:pathspec ‘xxx‘ did not match any file(s) known to git
在 escode 中进行分支切换时报如下错误 PS > git checkout xxx error: pathspec xxx did not match any file(s) known to git远程分支已经在 gitlab 客户端手动创建,在 escode 中也使用了拉取之类的操作,但是切换分支时依然报错。 解决方案 查看分…...

sed 保持空间命令之 x 的执行逻辑
目录 1. 将模式空间和保持空间的内容互换并打印 2. 将保持空间的内容交换回模式空间 3. 使用保持空间保存状态信息 4. 交换模式空间与保持空间隔行匹配 sed 有两个内置的缓存空间: 模式空间:该空间是 sed 内置的一个缓冲区,是 sed 执行的…...

按位异或^
在 Python 中,a ^ b 表示按位异或运算符。按位异或运算符对整数的每一位进行运算,如果对应位上的两个二进制数字不同,则结果为 1,否则为 0。 示例 a 5 # 二进制: 0101 b 3 # 二进制: 0011result a ^ b print(result) # 输…...
《企业实战分享 · 常用运维中间件》
📢 大家好,我是 【战神刘玉栋】,有10多年的研发经验,致力于前后端技术栈的知识沉淀和传播。 💗 🌻 近期刚转战 CSDN,会严格把控文章质量,绝不滥竽充数,如需交流ÿ…...

PyCharm 2024.1简介
PyCharm 2024.1 是JetBrains公司发布的Python集成开发环境(IDE)的最新版本。作为一个深受开发者欢迎的工具,PyCharm以其强大的功能和高效的开发体验著称。以下是PyCharm 2024.1的主要特性和改进: 1. **性能提升**: …...

终身免费的Navicat数据库,不需要破解,官方支持
终身免费的Navicat数据库,不需要破解,官方支持 卸载了Navicat,很不爽上干货,Navicat免费版下载地址 卸载了Navicat,很不爽 公司不让用那些破解的数据库软件,之前一直使用Navicat。换了几款其他的数据库试了…...

Spring Boot中的模板引擎选择与配置
Spring Boot中的模板引擎选择与配置 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来聊聊Spring Boot中的模板引擎选择与配置。模板引擎是生成动态网页…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
