「期末复习」线性代数
第一章 行列式
 的某一行(列)的元素都是两数之和,例如第i行的元素都是两数之和:
的某一行(列)的元素都是两数之和,例如第i行的元素都是两数之和:

矩阵



相关文章:

「期末复习」线性代数
第一章 行列式 行列式是一个数,是一个结果三阶行列式的计算:主对角线的乘积全排列与对换逆序数为奇就为奇排列,逆序数为偶就为偶排列对换:定理一:一个排列的任意两个元素对换,排列改变奇偶性(和…...
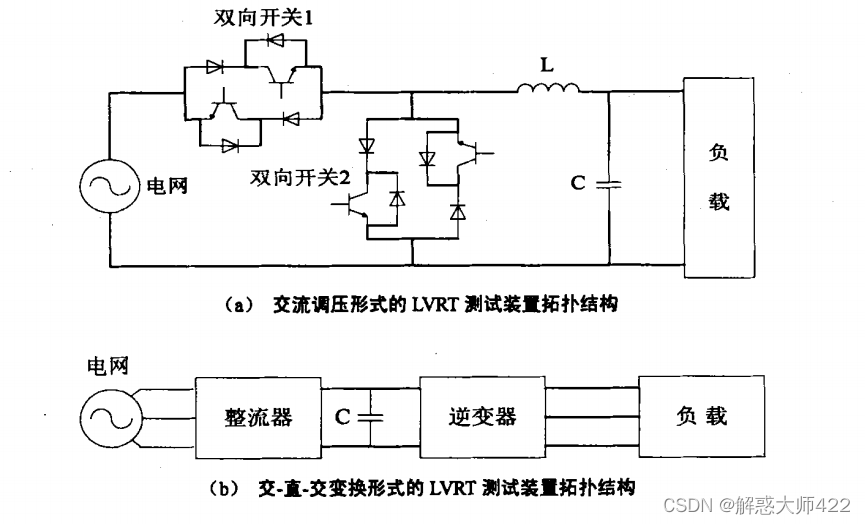
伏并网低电压穿越技术
国内光伏并网低电压穿越要求 略: 低电压穿越方法 当前,光伏电站实现低电压穿越可通过两种方式,即增加硬件设备或者改变控制策略。本节对基于储能设备、基于无功补偿设备、基于无功电流电压支撑控制策略三种实现LVRT的典型方法进行介绍。 …...
opencv的环境搭建
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...

C++智能指针
c11的三个智能指针 unique_ptr独占指针,用的最多 shared_ptr记数指针,其次 weak_ptr,shared_ptr的补充,很少用 引用他们要加上头文件#include unique_ptr独占指针: 1.只能有一个智能指针管理内存 2.当指针超出作用域…...
MongoDB--》MongoDB数据库以及可视化工具的安装与使用—保姆级教程
目录 数据库简介 MongoDB数据库的安装 MongoDB数据库的启动 MongoDB数据库环境变量的配置 MongoDB图形化管理工具 数据库简介 在使用MongoDB数据库之前,我们应该要知道我们使用它的原因: 在数据库当中,有常见的三高需求: Hi…...

JAVA 基础题
1. 面向对象有哪些特征?答:继承、封装、多态2. JDK与JRE的区别是什么?答:JDK是java开发时所需环境,它包含了Java开发时需要用到的API,JRE是Java的运行时环境,JDK包含了JRE,他们是包含…...

Flutter desktop端多屏幕展示问题处理
目前越来越多的人用Flutter来做桌面程序的开发,很多应用场景在Flutter开发端还不是很成熟,有些场景目前还没有很好的插件来支持,所以落地Flutter桌面版还是要慎重。 下面来说一下近期我遇到的一个问题,之前遇到一个需要双屏展示的…...

每天10个前端小知识 【Day 9】
👩 个人主页:不爱吃糖的程序媛 🙋♂️ 作者简介:前端领域新星创作者、CSDN内容合伙人,专注于前端各领域技术,成长的路上共同学习共同进步,一起加油呀! ✨系列专栏:前端…...

Elasticsearch的读写搜索过程
问题 Elasticsearch在读写数据的过程是什么样的?你该如何理解这个问题! Elasticsearch的写数据过程 客户端选择一个节点发送请求,这个时候我们所说的这个节点就是协调节点(coordinating node)协调节点对document进行了路由&am…...

线上服务质量的问题该如何去处理?你有什么思路?
线上服务质量的问题该如何去处理?你有什么思路? 目录:导读 发现线上故障 处理线上故障 修复线上故障 运营线上质量 就是前几天有个同学问了我一个问题:目前业内高可用部署主要采用方案? 看到这个问题,…...

IOC 配置,依赖注入的三种方式
xml 配置 顾名思义,就是将bean的信息配置.xml文件里,通过Spring加载文件为我们创建bean。这种方式出现很多早前的SSM项目中,将第三方类库或者一些配置工具类都以这种方式进行配置,主要原因是由于第三方类不支持Spring注解。 优点…...
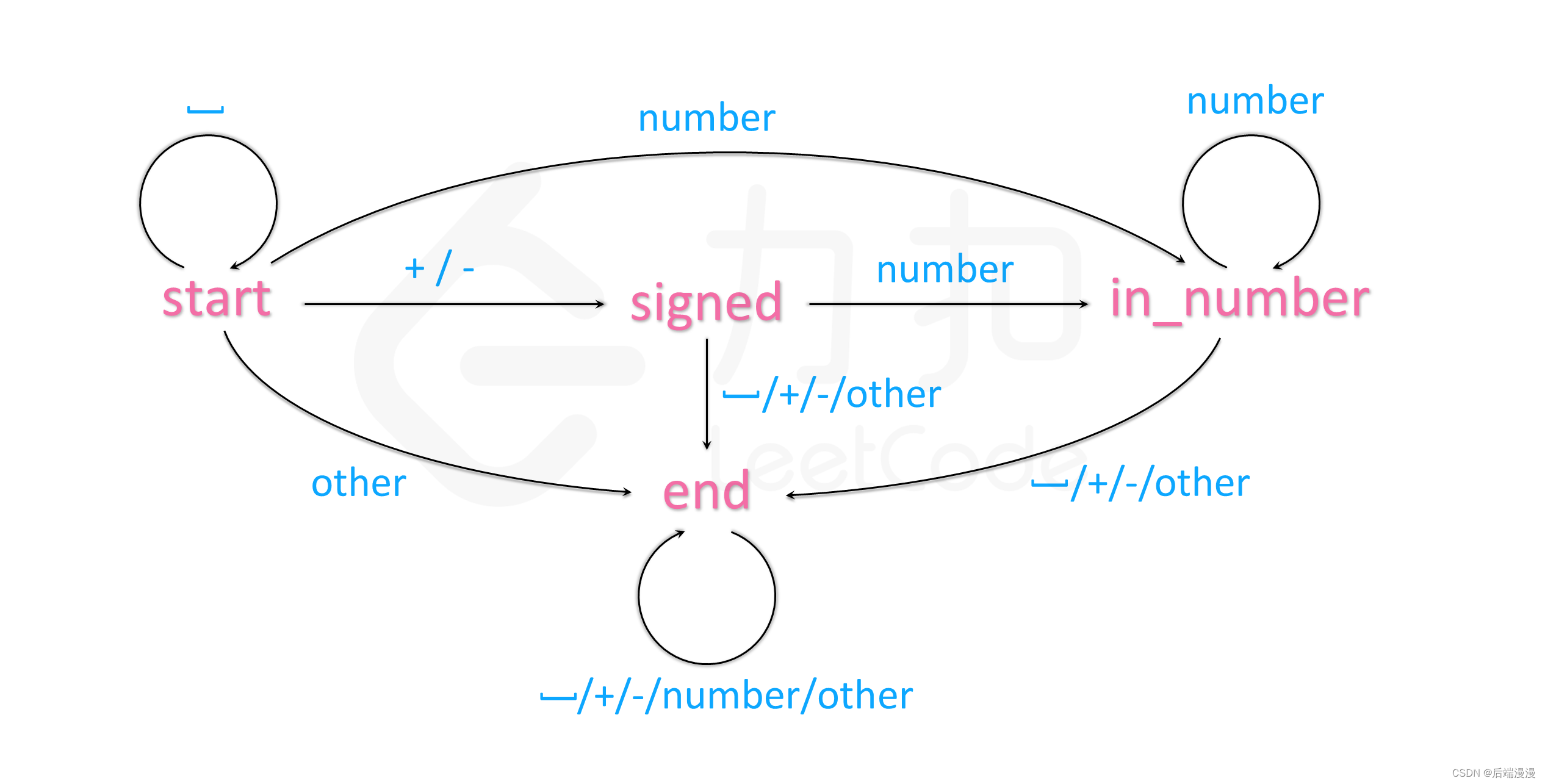
自动机,即有限状态机
文章目录一、问题来源二、题目描述三、题解中的自动机四、自动机学习五、有限状态机的使用场景一、问题来源 今天做力克题目的时候看到了字符串转换整数的一道算法题,其中又看到了题解中有自动机的概念,所以在这里对自动机做个笔记。题目链接 二、题目描…...
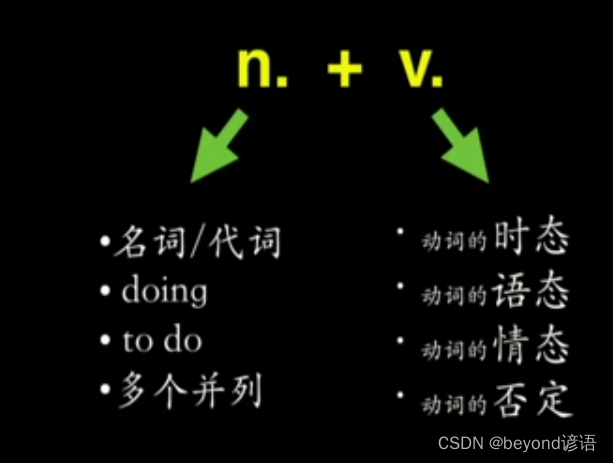
第一部分:简单句——第一章:简单句的核心——二、简单句的核心变化(主语/宾语/表语的变化)
二、简单句的核心变化 简单句的核心变化其实就是 一主一谓(n. v.) 表达一件事情,谓语动词是其中最重要的部分,谓语动词的变化主要有四种:三态加一否(时态、语态、情态、否定),其中…...

VSCode Markdown写作引入符合规范的参考文献
Markdown可以用来写论文,写论文的时候无一例外要用到参考文献,今天来谈谈怎么自动生成参考文献。之前讲了怎么导出的pdf,文章在这里 VSCode vscode-pandoc插件将中文Markdown转换为好看的pdf文档(使用eisvogel模板) …...
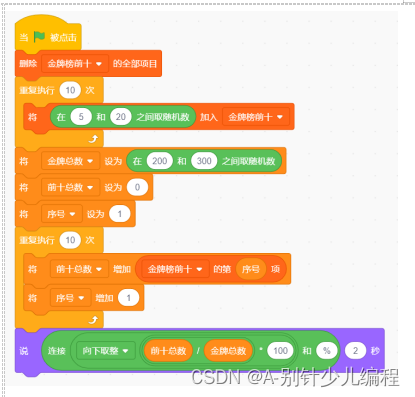
电子学会2022年12月青少年软件编程(图形化)等级考试试卷(四级)答案解析
目录 一、单选题(共15题,共30分) 二、判断题(共10题,共20分) 三、编程题(共3题,共50分) 青少年软件编程(图形化)等级考试试卷(四级) 一、单选题(共15题,共30分) 1. 运行下列程序…...

JUC并发编程学习笔记(一)——知识补充(Threadlocal和引用类型)
强引用、弱引用、软引用、虚引用 Java执行 GC(垃圾回收)判断对象是否存活有两种方式,分别是引用计数法和引用链法(可达性分析法)。 **引用计数:**Java堆中给每个对象都有一个引用计数器,每当某个对象在其它地方被引用时,该对象的…...

2022级上岸浙理工MBA的复试经验提炼和备考建议
在等待联考成绩出来的那段时间,虽然内心很忐忑,但还是为复试在积极的做准备,虽然也进行了估分大概有201分,但成绩和分数线没下来之前,只能尽量多做些一些准备把。因为笔试报了达立易考的辅导班,对于浙江理工…...

人大金仓数据库索引的应用与日常运维
索引的应用 一、常见索引及适应场景 BTREE索引 是KES默认索引,采用B树实现。 适用场景 范围查询和优化排序操作。 不支持特别长的字段。 HASH索引 先对索引列计算一个散列值(类似md5、sha1、crc32),然后对这个散列值以顺序…...

20230211英语学习
Six Lifestyle Choices to Slow Memory Decline 研究发现,生活方式真能帮助记忆“抗衰”? A combination of healthy lifestyle choices such as eating well, regularly exercising, playing cards and socialising at least twice a week may help sl…...

5G图书推荐
无线通信专业书籍推荐 1.无线通信原理:基于MATLAB的实践,作者:李珊,出版社:清华大学出版社 2.无线通信系统:原理、设计与应用,作者:肖宇,出版社:电子工业出版…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...
