Python28-5 k-means算法
k-means 算法介绍
k-means 算法是一种经典的聚类算法,其目的是将数据集分成 ( k ) 个不同的簇,每个簇内的数据点尽可能接近。算法的基本思想是通过反复迭代优化簇中心的位置,使得每个簇内的点与簇中心的距离之和最小。k-means 算法的具体步骤如下:
-
初始化:随机选择 ( k ) 个点作为初始簇中心。
-
分配簇:对于数据集中每一个点,计算其到所有簇中心的距离,并将其分配到最近的簇。
-
更新中心:重新计算每个簇的中心,即簇内所有点的平均值。
-
重复步骤2和3,直到簇中心不再发生变化或达到预设的迭代次数。
代码示例及可视化
以下是一个使用 Python 实现 k-means 算法并进行可视化的示例:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans# 生成示例数据
np.random.seed(42)
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)# 运行 k-means 算法
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)# 绘制结果
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')# 绘制簇中心
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75)
plt.title('k-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
运行结果:
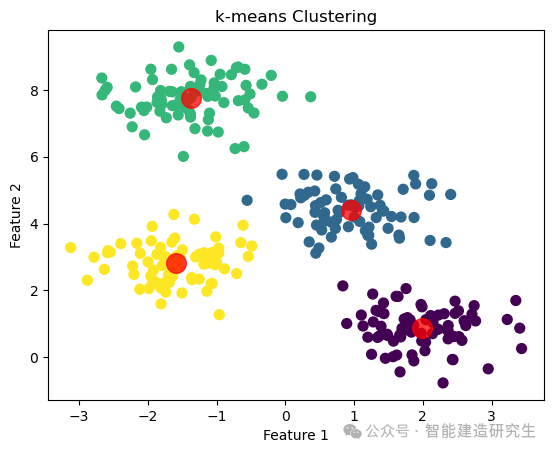
代码解释
-
数据生成:使用
make_blobs函数生成300个样本点,分成4个簇,每个簇的标准差为0.60。 -
k-means 算法:使用
KMeans类进行聚类,指定聚类数为4。通过fit方法对数据进行聚类,并用predict方法预测每个样本的簇。 -
可视化:使用 Matplotlib 绘制聚类结果。样本点根据其簇类别着色,并用红色标记簇中心。
这个示例展示了如何使用 k-means 算法对数据进行聚类,并通过可视化展示聚类结果和簇中心的位置。
以上内容总结自网络,如有帮助欢迎转发,我们下次再见!
相关文章:

Python28-5 k-means算法
k-means 算法介绍 k-means 算法是一种经典的聚类算法,其目的是将数据集分成 ( k ) 个不同的簇,每个簇内的数据点尽可能接近。算法的基本思想是通过反复迭代优化簇中心的位置,使得每个簇内的点与簇中心的距离之和最小。k-means 算法的具体步骤…...

主流国产服务器操作系统技术分析
主流国产服务器操作系统 信创 "信创",即信息技术应用创新,作为科技自立自强的核心词汇,在我国信息化建设的进程中扮演着至关重要的角色。自2016年起步,2020年开始蓬勃兴起,信创的浪潮正席卷整个信息与通信技…...
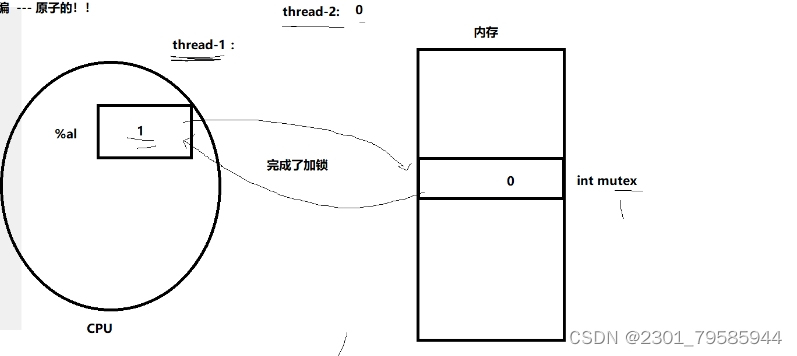
【Linux】线程封装与互斥(万字)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 文章目录 前言 C多线程的用法 对原生线程进行一次封装 理解pthread线程 Linux线程互斥 进程线程间的互斥相关背景概念 互斥量mutex 操作共享变量会有问题的售票…...

5分钟教你部署MySQL8.0环境
此方法基于Windows操作系统! 一、在MySQL官网单击downloads(下载)MySQLhttps://www.mysql.com/cn/ 选择在Windows操作系统下载 二、选择合适的版本 推荐下载第二种,安装时离线安装即可 三、安装MySQL8.0 1、找到MySQL下载完成…...

LLM应用:传统NLP任务
LLM出来以后,知乎上就出现了“传统NLP已死”的言论,但是传统NLP真的就被扔进历史的垃圾桶了吗? 其实,尽管LLM具有出色的通用能力,但仍然无法有效应对低资源领域的自然语言处理任务,如小语种翻译。为了更好地…...

基于Hadoop平台的电信客服数据的处理与分析③项目开发:搭建Kafka大数据运算环境---任务11:基础环境准备
任务描述 任务主要是安装配置基础环境,主要内容包括: 1、安装java Kafka和ZooKeeper都需要安装Java环境,推荐至少Java8及以上版本 2、安装ZooKeeper ZooKeeper是Kafka集群的必要组件 3、安装kafka Kafka版本包括使用的scala语言版本和kafka版…...

Golang中swtich中如何强制执行下一个代码块
switch 语句中的 case 代码块会默认带上 break,但可以使用 fallthrough 来强制执行下一个 case 代码块。 package mainimport ("fmt" )func main() {isSpace : func(char byte) bool {switch char {case : // 空格符会直接 break,返回 false…...
-第2节(启动和终止线程))
读书笔记-Java并发编程的艺术-第4章(Java并发编程基础)-第2节(启动和终止线程)
文章目录 4.2 启动和终止线程4.2.1 构造线程4.2.2 启动线程4.2.3 理解中断4.2.4 过期的suspend()、resume()和stop()4.2.5 安全地终止线程 4.2 启动和终止线程 在前面章节的示例中通过调用线程的start()方法进行启动,随着run()方法的执行完毕,线程也随之…...

通俗大白话理解Docker
什么是Docker Docker本质上是一种容器化技术,用于将应用程序及其所有依赖打包到一个标准化的单元中。这些单元(容器)可以在任何运行Docker的机器上运行。每个容器是相互隔离的,具有自己的文件系统、网络和进程空间。 以下是大白话…...
)
题解:CF1981C(Turtle and an Incomplete Sequence)
题解:CF1981C(Turtle and an Incomplete Sequence) Part 1:题意理解 地址链接:CF、洛谷。题面翻译:给定一个长度为 n n n 的序列 a a a,其中有一些元素未知,用 − 1 -1 −1 表示…...

Swift 中强大的 Key Paths(键路径)机制趣谈(上)
概览 小伙伴们可能不知道:在 Swift 语言中隐藏着大量看似“其貌不扬”实则却让秃头码农们“高世骇俗”,堪称卧虎藏龙的各种秘技。 其中,有一枚“不起眼”的小家伙称之为键路径(Key Paths)。如若将其善加利用ÿ…...

(十二)纹理和采样
纹理 在绘制三角形的过程中,将图片贴到三角形上进行显示的过程,就是纹理贴图的过程 uv坐标 如果如果图片尺寸和实际贴图尺寸不一致,就会导致像素不够用了的问题 纹理与采样 纹理对象(Texture):在GPU端,用来以一…...

QT创建地理信息shp文件编辑器shp_editor
空闲之余创建一个简单的矢量shp文件编辑器,加深对shp文件的理解。 一、启动程序 二、打开shp文件 三、显示shp文件的几何图形 四、双击右边表格中的feature,主窗体显示选中feature的各个节点。 五、鼠标在主窗体中选中feature的节点,按鼠标左…...
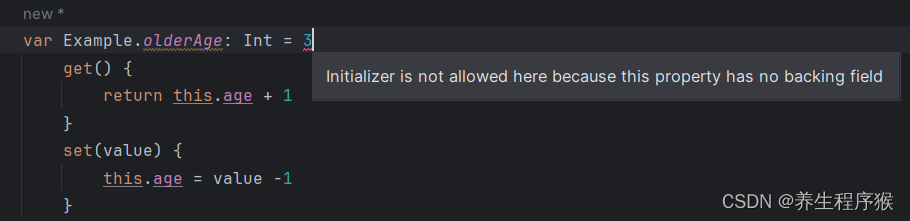
解析Kotlin中扩展函数与扩展属性【笔记摘要】
1.扩展函数 1.1 作用域:扩展函数写的位置不同,作用域就也不同 扩展函数可以写成顶层函数(Top-level Function),此时它只属于它所在的 package。这样你就能在任何类里使用它: package com.rengwuxianfun …...
【Java学习笔记】java图形界面编程
在前面的章节中,我们开发运行的应用程序都没有图形界面,但是很多应用软件,如Windows下的Office办公软件、扑克牌接龙游戏软件、企业进销存ERP系统等,都有很漂亮的图形界面。素以需要我们开发具有图形界面的软件。 Java图形界面编程…...
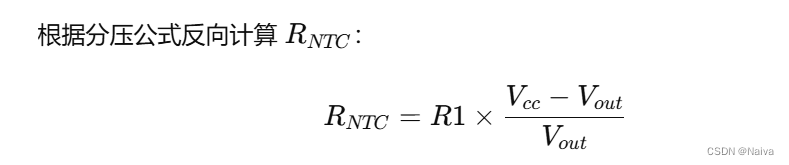
STM32入门笔记(03): ADC(SPL库函数版)(2)
A/D转换的常用技术有逐次逼近式、双积分式、并行式和跟踪比较式等。目前用的较多的是前3种。 A/D转换器的主要技术指标 转换时间 分辨率 例如,8位A/D转换器的数字输出量的变化范围为0~255,当输入电压的满刻度为5V时,数字量每变化…...
2024年7月2日 (周二) 叶子游戏新闻
老板键工具来唤去: 它可以为常用程序自定义快捷键,实现一键唤起、一键隐藏的 Windows 工具,并且支持窗口动态绑定快捷键(无需设置自动实现)。 卸载工具 HiBitUninstaller: Windows上的软件卸载工具 经典名作30周年新篇《恐怖惊魂夜…...

如何使用Spring Boot Profiles进行环境配置管理
如何使用Spring Boot Profiles进行环境配置管理 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将深入探讨如何利用Spring Boot Profiles来管理不同环境…...
)
Java错题归纳(二)
1、若有如下接口A的定义,下列哪些类下确实现了该接口:C interface A { void method1(int i); void method2(int j); } A class B implements A{ void method1( ) { } void method2( ) { } } B class B implements A { void method1(int i ) { }…...

Grafana面试题精选和参考答案
目录 Grafana是什么以及它的主要应用场景 Grafana支持的数据源 Grafana的体系结构及主要组件 Grafana如何实现数据的可视化和监控 Grafana支持的图表类型 如何在Grafana中创建和编辑仪表盘 Grafana的查询编辑器功能 Grafana支持的认证方式 Grafana的性能调优建议 Gra…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...
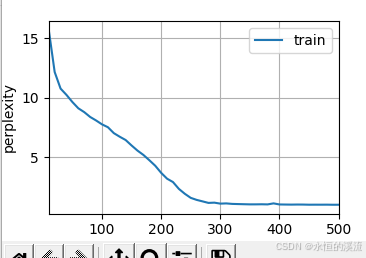
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...
