Python数据分析案例47——笔记本电脑价格影响因素分析
案例背景
博主对电脑的价格和配置一直略有研究,正好最近也有笔记本电脑相关的数据,想着来做点分析吧,写成一个案例。基本上描述性统计,画图,分组聚合,机器学习,交叉验证,搜索超参数那些。
数据介绍
这数据集室友给的,很像kaggle上的数据集,很规整,如下:
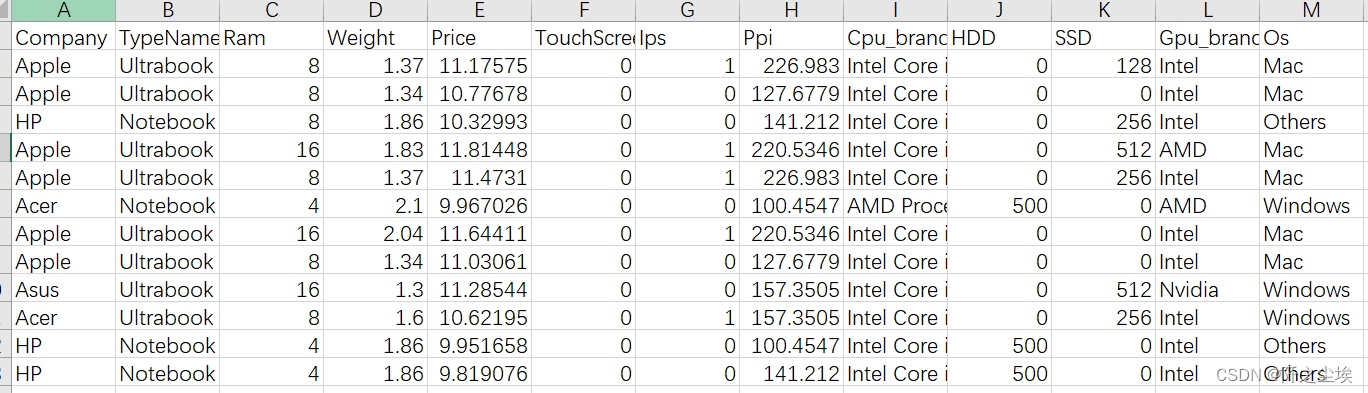
其中price是我们响应变量,其他都是X时特征变量。
需要该演示数据和全部代码文件的同学可以参考: 笔记本电脑
代码实现
数据分析四件套先导入:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as snsplt.rcParams ['font.sans-serif'] ='SimHei' #显示中文
plt.rcParams ['axes.unicode_minus']=False #显示负号读取数据,展示前五行
df=pd.read_csv('laptop_data_cleaned.csv')
df.head()
查看数据基础信息
df.info()
可以看到大概是13个变量,1273条数据,数据量不是很大。
简单整理一下变量的类别和含义的关系:
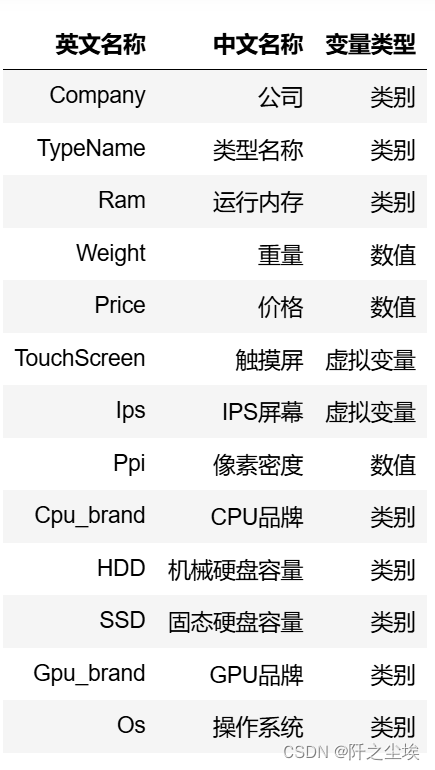
查看非数值型变量的描述性统计:
df.select_dtypes(exclude=['int','float']).describe()
数值型变量的描述性统计
df.describe()
下面进行初步分析:
类别变量画图
我们首先查看不同类别的变量的数量分布
# Select non-numeric columns
non_numeric_columns = df[['Company', 'TypeName', 'TouchScreen', 'Os','Cpu_brand','Gpu_brand' , 'Ram','HDD', 'SSD'] ].columns
f, axes = plt.subplots(3, 3, figsize=(10,10),dpi=128)
# Flatten axes for easy iterating
axes_flat = axes.flatten()
for i, column in enumerate(non_numeric_columns):if i < 9: sns.countplot(x=column, data=df, ax=axes_flat[i])axes_flat[i].set_title(f'Count of {column}')for label in axes_flat[i].get_xticklabels():label.set_rotation(90) #类别标签旋转一下,免得多了堆叠看不清# Hide any unused subplots
for j in range(i + 1, 9):f.delaxes(axes_flat[j])
plt.tight_layout()
plt.show()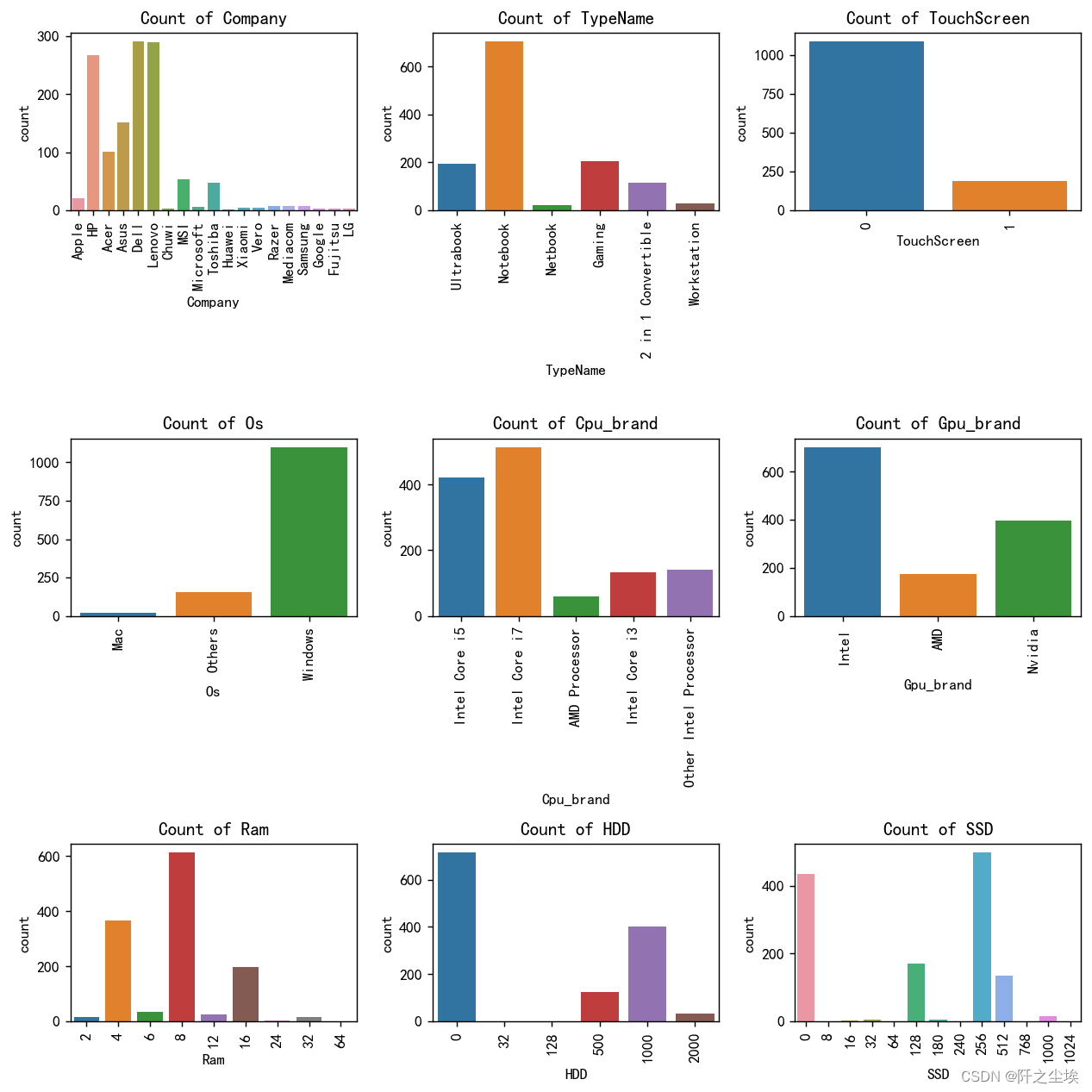
公司: 大多数笔记本电脑来自戴尔、联想和惠普品牌。 微软、三星等品牌的笔记本电脑较少。
类型名称: 超极本和笔记本是最常见的类型。 游戏本、二合一本、可转换本和工作站类型较少。
触摸屏: 大多数笔记本电脑没有触摸屏。 只有一小部分具有触摸屏功能。
操作系统: Windows 是最普遍的操作系统。 少数笔记本电脑使用 Mac 或其他操作系统。
处理器品牌: 英特尔酷睿 i5 和英特尔酷睿 i7 是最常见的 CPU 品牌。 AMD 处理器和其他英特尔处理器不太常见。
Gpu的牌子: 英特尔和 Nvidia GPU 最常用。 AMD GPU 不太常见。
内存: 8GB 和 16GB 内存是最常见的配置。 配备 4GB 和 12GB 内存的笔记本电脑较少。
机械硬盘: 大多数笔记本电脑没有机械硬盘或机械硬盘容量较小(32GB)。 少数笔记本电脑的机械硬盘容量较大(128GB、500GB、1000GB、2000GB)。
固态硬盘: 最常见的固态硬盘容量为 256GB 和 512GB。 也有一些笔记本电脑配备 128GB 或更大容量的固态硬盘,最高可达 1024GB。
关键结论:
- 数据表明,人们偏好某些品牌和配置,戴尔、联想和惠普是热门选择。
- 超极本和笔记本是主流类型,这可能是由于它们的多功能性和市场需求。
- Windows 操作系统比 Mac 和其他操作系统更受欢迎。
- 英特尔 CPU(尤其是酷睿 i5 和 i7)在市场上占据主导地位,而 AMD 则不太常见。
- 与 AMD 相比,Nvidia GPU 更受青睐。
- 8GB 和 16GB 内存的趋势表明,这些内存被认为是性能最佳的内存。
- 与硬盘相比,固态硬盘更受青睐,相当多的笔记本电脑采用 256GB 至 512GB 的固态硬盘。
数值型变量画图
画密度图
#画密度图,
num_columns = df[['Weight', 'Price','Ppi']].columns.tolist() # 列表头
dis_cols = 3 #一行几个
dis_rows = len(num_columns)
plt.figure(figsize=(3 * dis_cols, 2 * dis_rows),dpi=256)for i in range(len(num_columns)):ax = plt.subplot(dis_rows, dis_cols, i+1)ax = sns.kdeplot(df[num_columns[i]], color="skyblue" ,fill=True)ax.set_xlabel(num_columns[i],fontsize = 14)
plt.tight_layout()
#plt.savefig('训练测试特征变量核密度图',formate='png',dpi=500)
plt.show()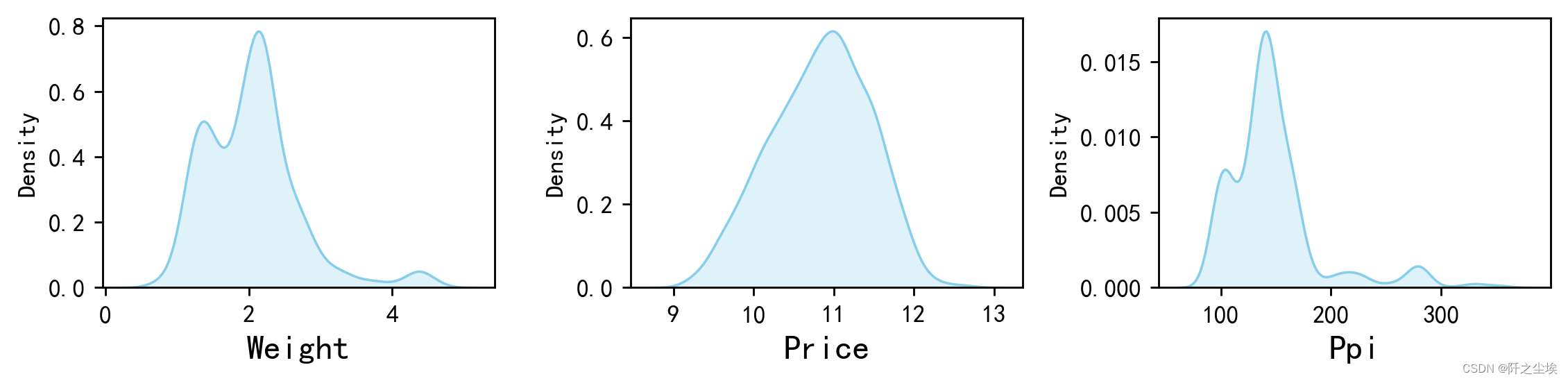
价格分布很均匀,PPI和重量有一些极大的异常点。
- 重量(Weight)的核密度图
从图中可以看出,笔记本电脑的重量主要集中在1到2.5公斤之间。 约在1.5公斤左右有一个峰值,表示大部分笔记本电脑的重量集中在这个范围。 在2.5公斤左右还有一个较小的峰值,说明有一部分笔记本电脑重量较重。 重量超过3公斤的笔记本电脑非常少见。
- 价格(Price)的核密度图
从图中可以看出,笔记本电脑的价格主要集中在10到11之间。 图中有一个明显的峰值,表示大部分笔记本电脑的价格集中在这个范围内。 价格在9到10之间和11到12之间的分布较少,但仍然有一定的密度。 价格超过12的笔记本电脑非常少见。
- PPI(Ppi)的核密度图
从图中可以看出,笔记本电脑的PPI主要集中在100左右。 在100 PPI左右有一个明显的峰值,表示大部分笔记本电脑的PPI集中在这个范围内。 图中显示了一些更高的PPI值(超过200),但这些笔记本电脑的数量较少。 PPI在200以上的笔记本电脑密度极低,几乎可以忽略不计。
总结 笔记本电脑的重量主要集中在1到2.5公斤之间,重量超过3公斤的笔记本电脑非常少见。 笔记本电脑的价格主要集中在10到11之间,价格超过12的笔记本电脑非常少见。 笔记本电脑的PPI主要集中在100左右,超过200 PPI的笔记本电脑数量极少。
画箱线图:
### 箱线图
plt.figure(figsize=(3 * dis_cols, 2.5 * dis_rows),dpi=128)
for i in range(len(num_columns)):plt.subplot(dis_rows,dis_cols,i+1)sns.boxplot(data=df[num_columns[i]], orient="v",width=0.5)plt.xlabel(num_columns[i],fontsize = 14)
plt.tight_layout()
#plt.savefig('特征变量箱线图',formate='png',dpi=500)
plt.show()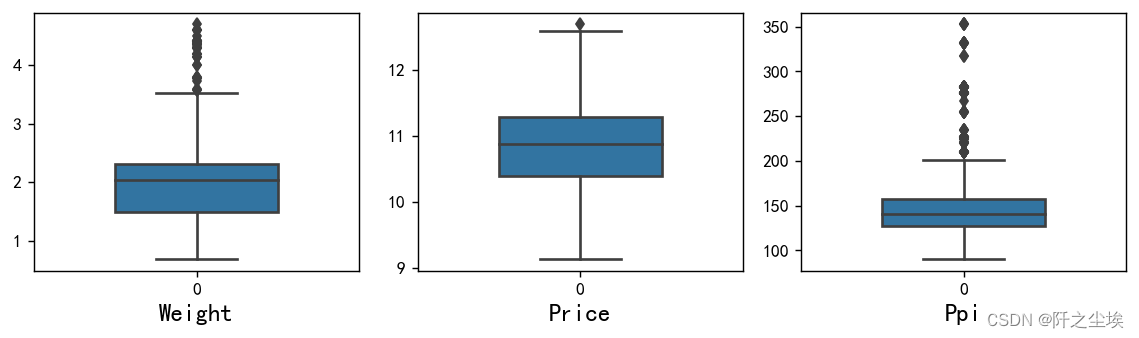
不同变量之间的分析
联合不同变量的分布,因为基本是价格影响因素,所以我们都是根据不同的类别去分析价格,所以都是分组聚合计算价格,我们直接画图
不同 的Company、TypeName、Cpu_brand、Gpu_brand的价格分布情况:
fig, axes = plt.subplots(2, 2, figsize=(14, 10), dpi=128)# 绘制第一个子图的小提琴图
sns.violinplot(ax=axes[0, 0], x='Company', y='Price', data=df)
axes[0, 0].set_title('不同牌子的电脑价格分布')
axes[0, 0].set_xlabel('牌子')
axes[0, 0].set_ylabel('价格')
axes[0, 0].set_xticklabels(axes[0, 0].get_xticklabels(), rotation=90)# 绘制第二个子图的小提琴图
sns.violinplot(ax=axes[0, 1], x='TypeName', y='Price', data=df)
axes[0, 1].set_title('不同类型的电脑价格分布')
axes[0, 1].set_xlabel('类型')
axes[0, 1].set_ylabel('价格')
axes[0, 1].set_xticklabels(axes[0, 1].get_xticklabels(), rotation=90)# 绘制第三个子图的小提琴图
sns.violinplot(ax=axes[1, 0], x='Cpu_brand', y='Price', data=df)
axes[1, 0].set_title('不同CPU的电脑价格分布')
axes[1, 0].set_xlabel('CPU')
axes[1, 0].set_ylabel('价格')
axes[1, 0].set_xticklabels(axes[1, 0].get_xticklabels(), rotation=90)# 绘制第四个子图的小提琴图
sns.violinplot(ax=axes[1, 1], x='Gpu_brand', y='Price', data=df)
axes[1, 1].set_title('不同GPU的电脑价格分布')
axes[1, 1].set_xlabel('GPU')
axes[1, 1].set_ylabel('价格')
axes[1, 1].set_xticklabels(axes[1, 1].get_xticklabels(), rotation=90)# 调整子图之间的间距
plt.tight_layout()# 显示图形
plt.show()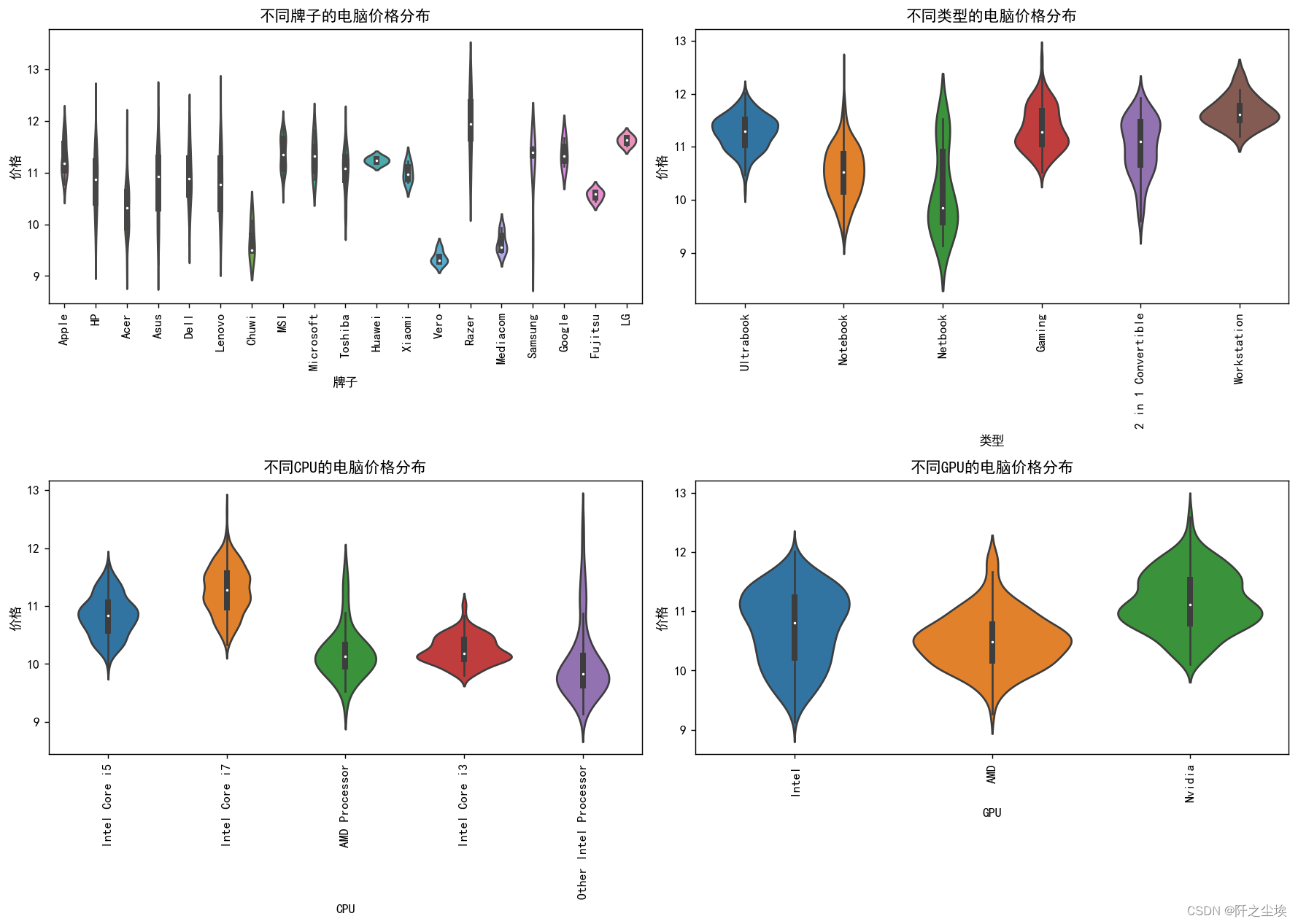
1.不同品牌的电脑价格分布
该图展示了各个品牌的笔记本电脑价格分布情况。 从图中可以看出,Microsoft、LG、Apple等品牌的电脑价格普遍较高。 华为(Huawei)、小米(Xiaomi)等品牌的价格较为集中且偏低。 Dell和Lenovo的价格分布较广,表明它们的产品线覆盖了从低端到高端的多个价格区间。 部分品牌如Chuwi、Vero等价格分布范围较小,表明它们的产品种类可能较少或集中在某一价格区间。
2.不同类型的电脑价格分布
该图展示了不同类型笔记本电脑的价格分布情况。 2 in 1 Convertible(二合一的笔记本)和Ultrabook的价格普遍较高,尤其是Ultrabook,价格范围较大且中位数较高。 Netbook的价格最低且分布范围较窄,表明这类电脑价格较为统一,主要集中在低价区间。 Gaming(游戏本)的价格分布范围较大,说明有从中端到高端不同价格的产品。 Workstation(工作站)的价格也较高且分布范围广,反映出其高性能和专业用途的特点。
3.不同CPU品牌的电脑价格分布
该图展示了不同CPU品牌的笔记本电脑价格分布情况。 Intel Core i7的电脑价格最高且分布范围广,反映出其高性能带来的高价格。 AMD Processor的价格分布较低且范围较小,说明使用AMD处理器的笔记本电脑价格较为集中且偏低。 Intel Core i5的价格分布居中且范围适中,表明这类笔记本电脑覆盖了中端市场。 其他Intel Processor的价格分布范围较大,说明使用其他Intel处理器的笔记本电脑有不同的市场定位。
4.不同GPU品牌的电脑价格分布
该图展示了不同GPU品牌的笔记本电脑价格分布情况。 使用Intel GPU的笔记本电脑价格分布范围最广,覆盖了从低端到高端的多个价格区间。 使用Nvidia GPU的价格较高且分布集中,反映出其高性能和高价位的特点。 使用AMD GPU的价格分布较宽,说明其产品线覆盖了从中低端到高端不同价格的市场。 总体来看,不同品牌、类型、CPU品牌和GPU品牌的笔记本电脑在价格上都有较明显的分布特点,反映出市场上不同定位和需求的产品特征。这些分布图可以帮助消费者在选择笔记本电脑时,更好地了解不同产品的价格定位,从而做出更加符合自身需求的选择。
研究不同的 'TouchScreen', 'Ram','HDD', 'SSD' 下的价格
fig, axes = plt.subplots(2, 2, figsize=(14, 8), dpi=128)# 绘制 TouchScreen 与 Price 的散点图
sns.scatterplot(ax=axes[0, 0], x='TouchScreen', y='Price', data=df, hue='TouchScreen',palette='brg')
axes[0, 0].set_title('TouchScreen 与 Price 的关系')
axes[0, 0].set_xlabel('TouchScreen')
axes[0, 0].set_ylabel('Price')
axes[0, 0].legend(title='TouchScreen')# 绘制 Ram 与 Price 的散点图
sns.scatterplot(ax=axes[0, 1], x='Ram', y='Price', data=df, hue='Ram', palette='viridis')
axes[0, 1].set_title('Ram 与 Price 的关系')
axes[0, 1].set_xlabel('Ram')
axes[0, 1].set_ylabel('Price')
axes[0, 1].legend(title='Ram')# 绘制 HDD 与 Price 的散点图
sns.scatterplot(ax=axes[1, 0], x='HDD', y='Price', data=df, hue='HDD', palette='plasma')
axes[1, 0].set_title('HDD 与 Price 的关系')
axes[1, 0].set_xlabel('HDD')
axes[1, 0].set_ylabel('Price')
axes[1, 0].legend(title='HDD')# 绘制 SSD 与 Price 的散点图
sns.scatterplot(ax=axes[1, 1], x='SSD', y='Price', data=df, hue='SSD', palette='coolwarm')
axes[1, 1].set_title('SSD 与 Price 的关系')
axes[1, 1].set_xlabel('SSD')
axes[1, 1].set_ylabel('Price')
axes[1, 1].legend(title='SSD')plt.tight_layout()
# 显示图形
plt.show()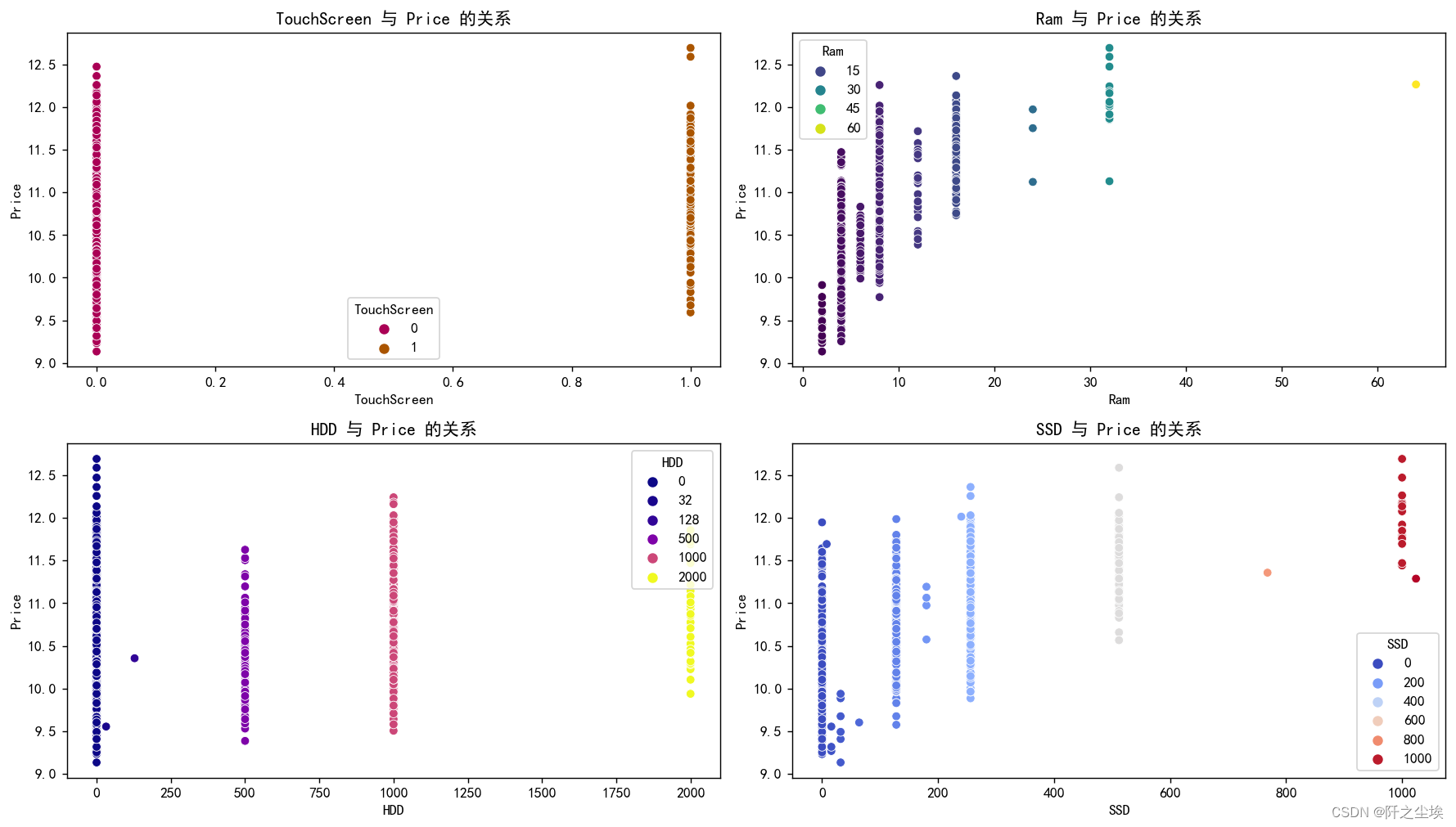
- TouchScreen 与 Price 的关系
该图展示了触摸屏(TouchScreen)与价格之间的关系。 从图中可以看出,有触摸屏的笔记本电脑(标记为1)的价格显著高于没有触摸屏的笔记本电脑(标记为0)。 这表明触摸屏功能会显著提高笔记本电脑的价格。
- Ram 与 Price 的关系
该图展示了内存大小(Ram)与价格之间的关系。 从图中可以看出,随着内存大小的增加,笔记本电脑的价格也在增加。 内存较大的笔记本电脑(如30GB及以上)的价格明显高于内存较小的笔记本电脑。 颜色深浅表示不同内存容量,可以看出内存容量越大,价格越高。
- HDD 与 Price 的关系
该图展示了硬盘容量(HDD)与价格之间的关系。 从图中可以看出,硬盘容量较大的笔记本电脑(如1000GB及以上)的价格显著高于硬盘容量较小的笔记本电脑(如0GB到500GB)。 硬盘容量为0的笔记本电脑价格分布较广,可能是因为这类笔记本电脑使用的是SSD而非HDD。 总体来说,HDD容量越大,笔记本电脑的价格也越高。
- SSD 与 Price 的关系
该图展示了固态硬盘(SSD)容量与价格之间的关系。 从图中可以看出,SSD容量较大的笔记本电脑(如1000GB)的价格明显高于SSD容量较小的笔记本电脑(如200GB及以下)。 没有SSD的笔记本电脑价格相对较低,但也有一定的分布范围。 整体上,SSD容量越大,笔记本电脑的价格越高。
总结
笔记本电脑的价格受到多个因素的影响,包括触摸屏功能、内存大小、HDD和SSD的容量。 拥有触摸屏的笔记本电脑价格普遍较高。 内存、HDD和SSD容量越大,笔记本电脑的价格越高。
数据清洗
数值型变量不需要处理,但是很多类别变量需要继续处理
df.select_dtypes(exclude=['int','float']).describe()可以看到现在5个类别变量之间的类别数量,company是19个,类别有点多,Company太多了,会造成维度较多,所以进行因子话,其他变量数量都是5,6个,可以直接进行独立热编码。
# 因子化 'Company' 列
df['Company'] = pd.factorize(df['Company'])[0].astype('int')
df['Company'].head()
可以看到数据变成了数值型变量。
# 独立热编码,然后查看变量的信息
# 独立热编码
data= pd.get_dummies(df)
data.info()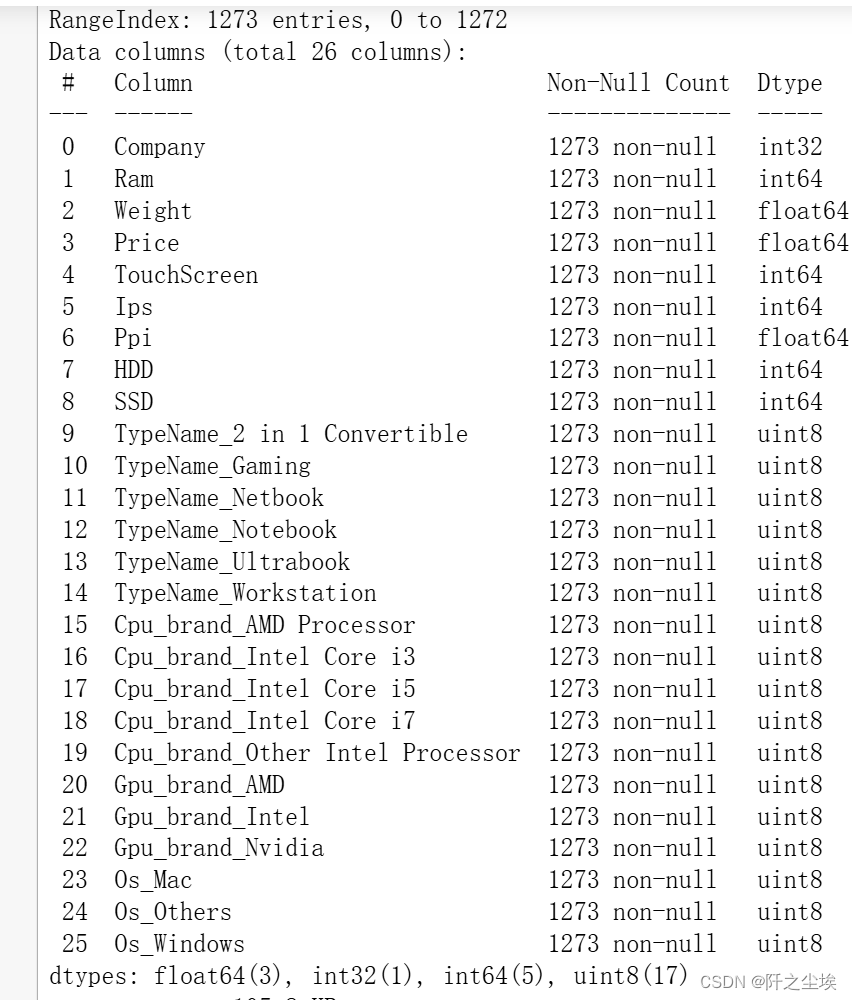
可以看到所有的数据都是数值型了,可以直接进行机器学习了。
开始机器学习
划分训练集和测试集
## 取出X和y
X=data.drop('Price',axis=1)
y=data['Price']划分训练集和验证集
#划分训练集和验证集
from sklearn.model_selection import train_test_split
X_train,X_val,y_train,y_val=train_test_split(X,y,test_size=0.2,random_state=0)数据标准化
#数据标准化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_s = scaler.transform(X_train)
X_val_s = scaler.transform(X_val)
print('训练数据形状:')
print(X_train_s.shape,y_train.shape)
print('验证数据形状:')
(X_val_s.shape,y_val.shape,)
模型选择
常见的手段了,十种模型一起训练
#采用十种模型,对比验证集精度
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import ElasticNet
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from xgboost.sklearn import XGBRegressor
from lightgbm import LGBMRegressor
from sklearn.svm import SVR
from sklearn.neural_network import MLPRegressor#线性回归
model1 = LinearRegression()#弹性网回归
model2 = ElasticNet(alpha=0.05, l1_ratio=0.5)#K近邻
model3 = KNeighborsRegressor(n_neighbors=10)#决策树
model4 = DecisionTreeRegressor(random_state=77)#随机森林
model5= RandomForestRegressor(n_estimators=500, max_features=int(X_train.shape[1]/3) , random_state=0)#梯度提升
model6 = GradientBoostingRegressor(n_estimators=500,random_state=123)#极端梯度提升
model7 = XGBRegressor(objective='reg:squarederror', n_estimators=1000, random_state=0)#轻量梯度提升
model8 = LGBMRegressor(n_estimators=1000,objective='regression', # 默认是二分类random_state=0,force_row_wise=True)#支持向量机
model9 = SVR(kernel="rbf")#神经网络
model10 = MLPRegressor(hidden_layer_sizes=(8,), random_state=7, max_iter=10000)model_list=[model1,model2,model3,model4,model5,model6,model7,model8,model9,model10]
model_name=['线性回归','惩罚回归','K近邻','决策树','随机森林','梯度提升','极端梯度提升','轻量梯度提升','支持向量机','神经网络']自定义评价函数
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error,r2_scoredef evaluation(y_test, y_predict):mae = mean_absolute_error(y_test, y_predict)mse = mean_squared_error(y_test, y_predict)rmse = np.sqrt(mean_squared_error(y_test, y_predict))mape=(abs(y_predict -y_test)/ y_test).mean()r_2=r2_score(y_test, y_predict)return mae, rmse, mape,r_2 #mse遍历,训练
df_eval=pd.DataFrame(columns=['MAE','RMSE','MAPE','R2'])
for i in range(len(model_list)):model_C=model_list[i]name=model_name[i]print(f'{name}正在训练...')model_C.fit(X_train_s, y_train)pred=model_C.predict(X_val_s)s=evaluation(y_val,pred)df_eval.loc[name,:]=list(s)
查看不同模型的数值型评价指标
df_eval
可视化:
bar_width = 0.4
colors=['c', 'b', 'g', 'tomato', 'm', 'y', 'lime', 'k','orange','pink','grey','tan','purple']
fig, ax = plt.subplots(2,2,figsize=(7,5),dpi=256)
for i,col in enumerate(df_eval.columns):n=int(str('22')+str(i+1))plt.subplot(n)df_col=df_eval[col]m =np.arange(len(df_col))#hatch=['-','/','+','x'],plt.bar(x=m,height=df_col.to_numpy(),width=bar_width,color=colors)#plt.xlabel('Methods',fontsize=12)names=df_col.indexplt.xticks(range(len(df_col)),names,fontsize=8)plt.xticks(rotation=40)if col=='R2':plt.ylabel(r'$R^{2}$',fontsize=14)else:plt.ylabel(col,fontsize=14)
plt.tight_layout()
#plt.savefig('柱状图.jpg',dpi=512)
plt.show()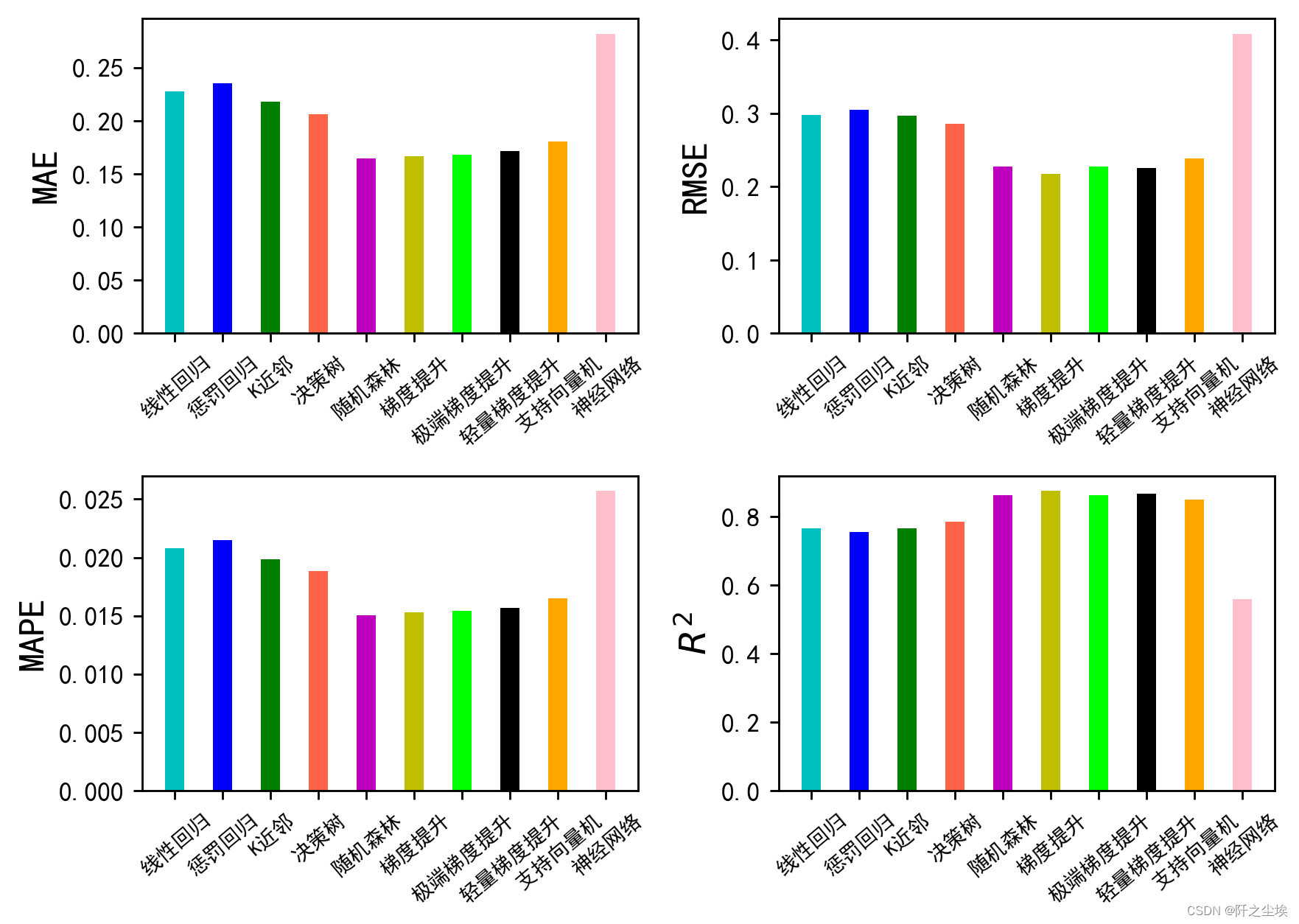 可能因为数据量不大,所以神经网络的效果不太好。基本都是树模型的效果最好,还是一样的经验,集成模型方法都是最好的,也就是XGB,LGBM,RF等。下面对他们进行交叉验证。
可能因为数据量不大,所以神经网络的效果不太好。基本都是树模型的效果最好,还是一样的经验,集成模型方法都是最好的,也就是XGB,LGBM,RF等。下面对他们进行交叉验证。
交叉验证
自定义一些交叉验证的函数
#回归问题交叉验证,使用拟合优度,mae,rmse,mape 作为评价标准
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error,r2_score
from sklearn.model_selection import KFolddef evaluation(y_test, y_predict):mae = mean_absolute_error(y_test, y_predict)mse = mean_squared_error(y_test, y_predict)rmse = np.sqrt(mean_squared_error(y_test, y_predict))mape=(abs(y_predict -y_test)/ y_test).mean()r_2=r2_score(y_test, y_predict)return mae, rmse, mape
def evaluation2(lis):array=np.array(lis)return array.mean() , array.std()def cross_val(model=None,X=None,Y=None,K=5,repeated=1):df_mean=pd.DataFrame(columns=['R2','MAE','RMSE','MAPE']) df_std=pd.DataFrame(columns=['R2','MAE','RMSE','MAPE'])for n in range(repeated):print(f'正在进行第{n+1}次重复K折.....随机数种子为{n}\n')kf = KFold(n_splits=K, shuffle=True, random_state=n)R2=[]; MAE=[] ; RMSE=[] ; MAPE=[]print(f" 开始本次在{K}折数据上的交叉验证.......\n")i=1for train_index, test_index in kf.split(X):print(f' 正在进行第{i}折的计算')X_train=X.values[train_index]y_train=y.values[train_index]X_test=X.values[test_index]y_test=y.values[test_index]model.fit(X_train,y_train)score=model.score(X_test,y_test)R2.append(score)pred=model.predict(X_test)mae, rmse, mape=evaluation(y_test, pred)MAE.append(mae)RMSE.append(rmse)MAPE.append(mape)print(f' 第{i}折的拟合优度为:{round(score,4)},MAE为{round(mae,4)},RMSE为{round(rmse,4)},MAPE为{round(mape,4)}')i+=1print(f' ———————————————完成本次的{K}折交叉验证———————————————————\n')R2_mean,R2_std=evaluation2(R2)MAE_mean,MAE_std=evaluation2(MAE)RMSE_mean,RMSE_std=evaluation2(RMSE)MAPE_mean,MAPE_std=evaluation2(MAPE)print(f'第{n+1}次重复K折,本次{K}折交叉验证的总体拟合优度均值为{R2_mean},方差为{R2_std}')print(f' 总体MAE均值为{MAE_mean},方差为{MAE_std}')print(f' 总体RMSE均值为{RMSE_mean},方差为{RMSE_std}')print(f' 总体MAPE均值为{MAPE_mean},方差为{MAPE_std}')print("\n====================================================================================================================\n")df1=pd.DataFrame(dict(zip(['R2','MAE','RMSE','MAPE'],[R2_mean,MAE_mean,RMSE_mean,MAPE_mean])),index=[n])df_mean=pd.concat([df_mean,df1])df2=pd.DataFrame(dict(zip(['R2','MAE','RMSE','MAPE'],[R2_std,MAE_std,RMSE_std,MAPE_std])),index=[n])df_std=pd.concat([df_std,df2])return df_mean,df_std训练lgbm
model = LGBMRegressor(n_estimators=200,objective='regression',random_state=1)
lgb_crosseval,lgb_crosseval2=cross_val(model=model,X=X,Y=y,K=5,repeated=6)训练xgboost
model = XGBRegressor(n_estimators=200,objective='reg:squarederror',random_state=0)
xgb_crosseval,xgb_crosseval2=cross_val(model=model,X=X,Y=y,K=5,repeated=6)
训练随机森林
model = RandomForestRegressor(n_estimators=200, max_features=int(X_train.shape[1]/3) , random_state=0)
rf_crosseval,rf_crosseval2=cross_val(model=model,X=X,Y=y,K=5,repeated=6)
四个评价指标的均值图
对三个模型的评价指标不同的交叉验证的均值
plt.subplots(1,4,figsize=(16,3))
for i,col in enumerate(lgb_crosseval.columns):n=int(str('14')+str(i+1))plt.subplot(n)plt.plot(lgb_crosseval[col], 'k', label='LGB')plt.plot(xgb_crosseval[col], 'b-.', label='XGB')plt.plot(rf_crosseval[col], 'r-^', label='RF')plt.title(f'不同模型的{col}对比')plt.xlabel('重复交叉验证次数')plt.ylabel(col,fontsize=16)plt.legend()
plt.tight_layout()
plt.show()
均值上来看LGBM的效果最好,R2大,误差指标低。
四个评价指标的方差图
plt.subplots(1,4,figsize=(16,3))
for i,col in enumerate(lgb_crosseval2.columns):n=int(str('14')+str(i+1))plt.subplot(n)plt.plot(lgb_crosseval2[col], 'k', label='LGB')plt.plot(xgb_crosseval2[col], 'b-.', label='XGB')plt.plot(rf_crosseval2[col], 'r-^', label='RF')plt.title(f'不同模型的{col}方差对比')plt.xlabel('重复交叉验证次数')plt.ylabel(col,fontsize=16)plt.legend()
plt.tight_layout()
plt.show()
方差差不多,模型的稳定性都差不多。
均值上来看LGBM的效果最好,下面对LGBM搜索超参数。
搜超参数
k折交叉验证,随机超参数搜索
#利用K折交叉验证搜索最优超参数
from sklearn.model_selection import KFold, StratifiedKFold
from sklearn.model_selection import GridSearchCV,RandomizedSearchCV超参数搜索
# Choose best hyperparameters by RandomizedSearchCV
#随机搜索的参数
param_distributions = {'max_depth': range(5, 8), 'subsample':np.linspace(0.5,1,5 ),'num_leaves': [15, 31, 63,],'colsample_bytree': [0.6, 0.7, 0.8, 1.0],'learning_rate': np.linspace(0.05,0.3,6 ), 'n_estimators':[100,200,300,400,500]}# 'min_child_weight':np.linspace(0,0.1,2 ),
kfold = KFold(n_splits=5, shuffle=True, random_state=1)
randomsearch=RandomizedSearchCV(estimator= LGBMRegressor(objective='regression',random_state=0,verbosity=-1),param_distributions=param_distributions, n_iter=100)
randomsearch.fit(X_train_s, y_train)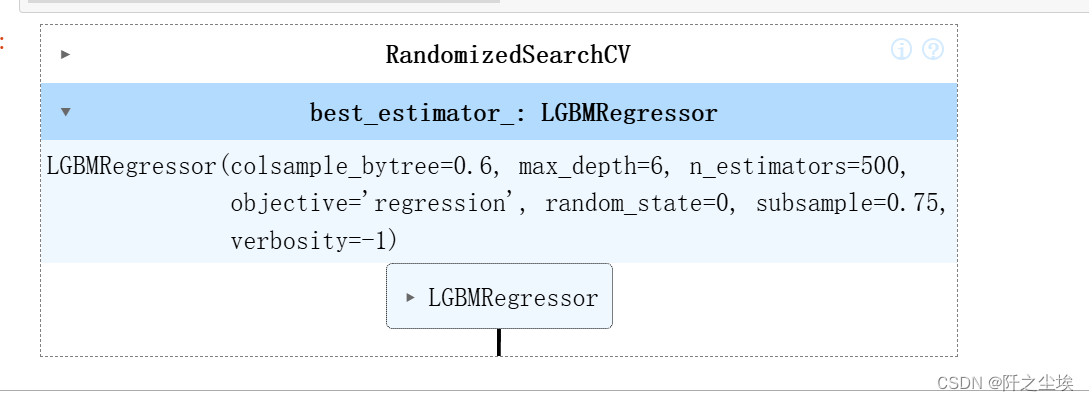
查看最好的模型参数
randomsearch.best_params_
带入最好的参数模型训练和测试:
best_estimator = randomsearch.best_estimator_
best_estimator.score(X_val_s, y_val)
#利用找出来的最优超参数在所有的训练集上训练,然后预测
model=LGBMRegressor(objective='regression',subsample=0.75,learning_rate= 0.1,n_estimators= 500,num_leaves=31,max_depth= 6,colsample_bytree=0.6,random_state=0,verbosity=-1)
model.fit(X_train_s, y_train)
model.score(X_val_s, y_val)
变量重要性排序图
最好的模型,在全部数据上给进行训练
model=LGBMRegressor(objective='regression',subsample=0.75,learning_rate= 0.1,n_estimators= 500,num_leaves=31,max_depth= 6,colsample_bytree=0.6,random_state=0,verbosity=-1)
model.fit(X.to_numpy(),y.to_numpy())
model.score(X.to_numpy(), y.to_numpy())然后取出变量重要性,排序画图
sorted_index = model.feature_importances_.argsort()[::-1]
plt.figure(figsize=(10, 8),dpi=128) # 可以调整尺寸以适应所有特征# 使用 seaborn 来绘制条形图
sns.barplot(x=model.feature_importances_[sorted_index], y=X.columns[sorted_index], orient='h')
plt.xlabel('Feature Importance') # x轴标签
plt.ylabel('Feature') # y轴标签
plt.show()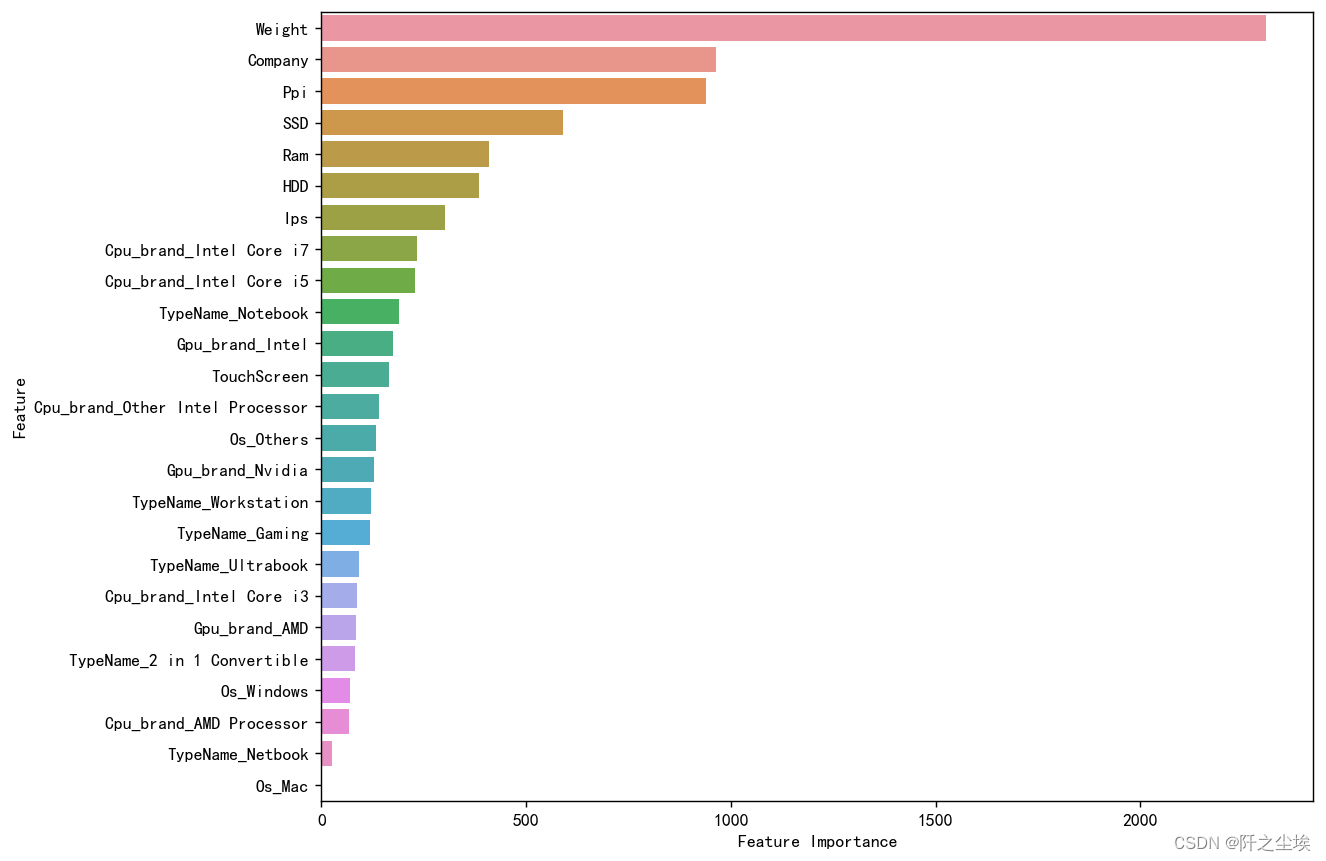
分析如下:
Weight(重量): 重量是最重要的特征,表明重量对电脑价格有显著影响。较轻的电脑通常设计更为紧凑,使用了高端材料和技术,从而增加了成本。 轻便的设计是便携设备的一个重要特征,尤其是对需要经常携带电脑的用户。
Company(公司): 品牌对价格的影响也非常大。不同品牌在设计、制造和市场定位上有显著差异,进而反映在价格上。 选择知名品牌的电脑可能提供更好的质量、售后服务和用户体验,但通常价格也更高。
Ppi(像素密度): 像素密度表示屏幕的清晰度。高像素密度的屏幕通常用于高端设备,提供更好的显示效果,但也会增加成本。 对于需要高质量显示效果的用户,如设计师和多媒体编辑,选择高PPI的屏幕是值得的。
SSD(固态硬盘): 固态硬盘的容量和存在对价格有重要影响。SSD提供更快的读写速度和更好的耐用性,因此价格较高。 选择较大容量的SSD可以显著提升电脑性能和用户体验,但也要考虑成本因素。
Ram(内存): 内存容量对价格的影响较大。较大的内存意味着更高的计算能力和多任务处理能力,因此会提高电脑价格。 对于需要处理大量数据或运行多个程序的用户,大容量内存是必不可少的。
HDD(机械硬盘): 机械硬盘容量对价格也有一定影响。尽管SSD更受欢迎,但大容量HDD依然是存储大量数据的经济选择。 对于需要大量存储空间的用户,可以选择搭配SSD和HDD的混合存储方案。
Ips(IPS屏幕): IPS屏幕提供更好的视角和颜色表现,但也会增加成本,从而提高电脑价格。 对于需要高质量显示效果的用户,IPS屏幕是一个重要特征。
Cpu_brand_Intel Core i7: Intel Core i7处理器是高端处理器,通常用于高性能电脑,对价格有显著影响。 高性能处理器意味着更高的处理速度和更强的计算能力,这在一定程度上反映了产品的高端定位。
Cpu_brand_Intel Core i5: Intel Core i5处理器虽然性能不如i7,但在主流市场上有较高的性价比,对价格也有显著影响。 对于预算有限但需要较高性能的用户,i5处理器是一个不错的选择。
TypeName_Notebook(笔记本类型): 笔记本类型对价格也有重要影响。不同类型的笔记本(如普通笔记本、游戏本、超极本等)在设计和性能上有显著差异,进而影响价格。 选择合适类型的笔记本应根据具体用途和预算进行权衡。 其他特征如显卡品牌、触摸屏、操作系统等也对价格有一定影响,但相对较低。这些特征可以根据具体需求进行选择,以获得最优的性价比和使用体验。
结论 从变量重要性图中可以看出,重量、品牌和像素密度是影响电脑价格的主要因素。这些特征显著提升了电脑的性能和用户体验,因此对价格有较大影响。其他特征如SSD、内存和处理器类型等也对价格有重要影响,应根据具体需求和预算综合考虑这些因素。
在选择电脑时,优先考虑这些关键特征,可以在保证性能的同时控制成本,获得最优的使用体验。
创作不易,看官觉得写得还不错的话点个关注和赞吧,本人会持续更新python数据分析领域的代码文章~(需要定制类似的代码可私信)
相关文章:

Python数据分析案例47——笔记本电脑价格影响因素分析
案例背景 博主对电脑的价格和配置一直略有研究,正好最近也有笔记本电脑相关的数据,想着来做点分析吧,写成一个案例。基本上描述性统计,画图,分组聚合,机器学习,交叉验证,搜索超参数…...

【加密与解密】【09】GPG Client签名流程
什么是GPG客户端 GPG客户端是实现PGP加密协议的一套客户端程序,可用于加密或签名 下载GPG客户端 建议安装命令行工具,图形工具一般不具备完整功能 https://gnupg.org/download/index.html生成私钥 此时会要求你输入名称,邮箱,…...

“2024软博会” 为软件企业提供集展示、交流、合作一站式平台
随着全球科技浪潮的涌动,软件行业正迎来前所未有的发展机遇,成为了全球新一轮竞争的“制高点”,以及未来经济发展的“增长点”。在当前互联网、大数据、云计算、人工智能、区块链等技术加速创新的背景下,数字经济已经渗透到经济社…...

【Zoom安全解析】深入Zoom的端到端加密机制
标题:【Zoom安全解析】深入Zoom的端到端加密机制 在远程工作和在线会议变得越来越普及的今天,视频会议平台的安全性成为了用户关注的焦点。Zoom作为全球领先的视频会议软件,其端到端加密(E2EE)功能保证了通话的安全性…...

7 动态规划
下面的例子不错: 对于动态规划,能学到不少东西; 你要清楚每一步都在做什么,划分细致就能够拆解清楚! xk. - 力扣(LeetCode) labuladong的算法笔记-动态规划-CSDN博客 动态规划是…...

.net 快速开发框架开源
DF.OpenAPI开源系统 前后端分离,开箱即用,java经典功能.net也具备 系统介绍 DF.OpenAPI是基于Admin.NET二开的,是一个开源的多租户后台管理系统。采用前后端分离技术(前端使用vue.js,后端使用.net 3~.net6ÿ…...

《昇思25天学习打卡营第06天|网络构建》
网络构建 神经网络模型由神经网络层和Tensor操作构成 #实验环境已经预装了mindspore2.2.14,如需更换mindspore版本,可更改下面mindspore的版本号 !pip uninstall mindspore -y !pip install -i https://pypi.mirrors.ustc.edu.cn/simple mindspore2.2.…...

【链表】- 两两交换链表中的节点
1. 对应力扣题目连接 两两交换链表中的节点 2. 实现案例代码 public class ExchangeLinkedListsPairwise {public static void main(String[] args) {// 示例链表:[1, 2, 3, 4]ListNode head new ListNode(1);head.next new ListNode(2);head.next.next new L…...
——抽象工厂模式)
java设计模式(四)——抽象工厂模式
一、模式介绍 改善在工厂方法模式中,扩展时新增产品类、工厂类,导致项目中类巨多的场面,减少系统的维护成本,且一个工厂可以生成多种产品,而不是同一种的产品,比如一个工厂既可以生产鞋子又可以衣服,而不是只能生产鞋子。 二、工厂方法模式 1、实现步骤 第一步: 定义…...

动物检测yolo格式数据集(水牛 、大象 、犀牛 、斑马四类)
动物检测数据集 1、下载地址: https://download.csdn.net/download/qq_15060477/89512588?spm1001.2101.3001.9500 2、数据集介绍 本数据集含有四种动物可以检测,分别是水牛 、大象 、犀牛 、斑马四类,数据集格式为yolo格式,…...

昇思25天学习打卡营第05天 | 数据变换 Transforms
昇思25天学习打卡营第05天 | 数据变换 Transforms 文章目录 昇思25天学习打卡营第05天 | 数据变换 TransformsCommon TransformsCompose Vision TransformsText TransformPythonTokenizerLookup Lambda Transforms数据处理模式Pipeline模式Eager模式 总结打卡 通常情况下的原始…...
Springboot+MySQL 公寓报修管理系统源码
功能结构图 效果图:...

jenkins 发布服务到linux服务器
1.环境准备 1.1 需要一台已经部署了jenkins的服务器,上面已经集成好了,jdk、maven、nodejs、git等基础的服务。 1.2 需要安装插件 pusblish over ssh 1.3 准备一台额外的linux服务器,安装好jdk 2.流程描述 2.1 配置jenkins,包括p…...
Appium+python自动化(三十九)-Appium自动化测试框架综合实践 - 代码实现(超详解)
1.简介 今天我们紧接着上一篇继续分享Appium自动化测试框架综合实践 - 代码实现。由于时间的关系,宏哥这里用代码给小伙伴演示两个模块:注册和登录。 2.业务模块封装 因为现在各种APP的层出不群,各式各样的。但是其大多数都有注册、登录。为…...

防止跨站脚本攻击XSS之Antisamy
目录 一、什么是跨站脚本攻击(XSS) 二、通常有哪些解决方案 三、常见的XSS攻击例子有哪些 3.1 存储型XSS攻击(黑产恶意截流,跳转不法网站) 3.2反射型XSS攻击: 四、什么是跨站请求伪造? 五…...

Python爬虫实战案例——王者荣耀皮肤抓取
大家好,我是你们的老朋友——南枫,今天我们一起来学习一下该如何抓取大家经常玩的游戏——王者荣耀里面的所有英雄的皮肤。 老规矩,直接上代码: 导入我们需要使用到的,也是唯一用到的库: 我们要抓取皮肤其…...

PyTorch计算机视觉实战:目标检测、图像处理与深度学习
本书基于真实数据集,全面系统地阐述现代计算机视觉实用技术、方法和实践,涵盖50多个计算机视觉问题。全书分为四部分:一部分介绍神经网络和PyTorch的基础知识,以及如何使用PyTorch构建并训练神经网络,包括输入数据缩放…...
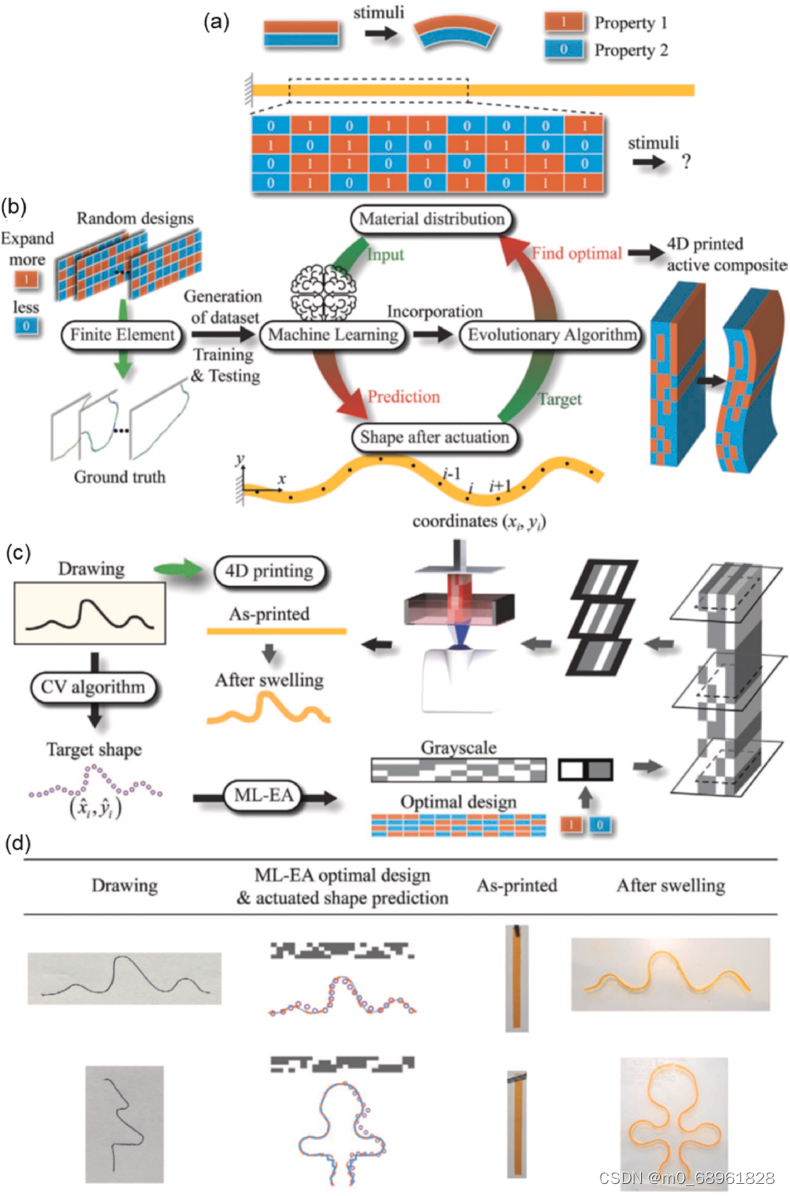
4D 生物打印:将时间维度融入,打造个性化动态组织
4D 生物打印技术将时间维度融入 3D 生物打印,赋予打印出的结构动态变化的能力,使其更接近于真实组织和器官的特性。要实现这一目标,需要使用智能生物材料和智能设计策略。 智能生物材料 目前用于 4D 生物打印的智能生物材料主要包括形状记忆…...

银行清算业务功能测试解析
银行清算业务是指银行间通过账户或有关货币当地清算系统,在办理结算和支付中用以清讫双边或多边债权债务的过程和方法。按地域划分,清算业务可分为国内联行清算和国际清算。常见的清算模式包括实时全额清算、净额批量清算、大额资金转账系统及小额定时清…...

CVE-2024-6387漏洞预警:尽快升级OpenSSH
OpenSSH维护者发布了安全更新,其中包含一个严重的安全漏洞,该漏洞可能导致在基于glibc的Linux系统中使用root权限执行未经身份验证的远程代码。该漏洞的代号为regreSSHion,CVE标识符为CVE-2024-6387。它驻留在OpenSSH服务器组件(也…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
