算法第十七期——状态规划(DP)之动态压缩
一、总述
状态压缩动态规划,就是我们俗称的状压DP,是利用计算机二进制的性质来描述状态的一种DP方式。
- 应用背景:以集合为状态,且集合可以用二进制来表示,用二进制的位运算来处理。
- 集合问题一般是指数复杂度的,例如:(1)子集问题,设元素无先后关系,那么共有
个子集;(2)排列问题,对所有元素进行全排列,共有n!个全排列。
- 状态压缩DP:集合的状态(子集或排列),如果用二进制表示状态,并用二进制的位运算来遍历和操作,又简单又快。
- 题目的数据范围不超过100
很多棋盘问题都运用到了状压,同时,状压也很经常和BFS及DP连用。
状压dp其实就是将状态压缩成2进制来保存,其特征就是看起来有点像搜索,每个格子的状态只有1或0 ,是另一类非常典型的动态规划
举个例子:有一个大小为n*n的农田,我们可以在任意处种田,现在来描述一下某一行的某种状态:
设n = 9;有二进制数 100011011(九位),每一位表示该农田是否被占用,1表示用了,0表示没用,这样一种状态就被我们表示出来了:见下表
2、位运算
用位运算做集合操作
判断a的第i位(从最低位开始数)是否等于1: 1<<( i -1 ) ) & a
把a的第i位改成1: a | ( 1<<(i-1) )
把a的第i位改成0: a &(~(1<<i) )
把a的最后一个1去掉: a& (a-1)
a = 213;b = 45 # a = 1101 0101,b = 0010 1101
print("a & b =", a & b) # AND = 5,二进制0001 0101
print("a | b =",a | b) # OR= 253,二进制1111 1101
print("a^ b =",a^ b) # XOR= 248,二进制1100 1100
print("a << 2 =", a<< 2) # a*4= 852,二进制0011 0101 0100
print("a >> 2=", a >> 2) # a/4 = 53,二进制0011 0101i = 5 # a的第i位是否为1
if((1 << (i-1)) & a): print("a[%d]=%d"%(i,1));#a的第i位是1
else: print("a[%d]=%d"%(i,O));#a的第i位是0a = 43;i = 5 #a = 0010 1011
print("a=", a |(1<<(i-1))) # 把a的第i位改成1。a=59,二进制0011 1011
print("a=", a &(~(1<<(i-1)))) # 把a的第i位改成0a = 242 # 把a最后的1去掉。 a =1111 0010
print("a=", a & (a-1)) # 去掉最后的1。=240,二进制1111 0000
3、引导题:糖果
2019年省赛
题目描述
糖果店的老板一共有 M 种口味的糖果出售。为了方便描述,我们将 M 种口味编号 1∼ M。
小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果,而是 K 颗一包整包出售。幸好糖果包装上注明了其中 K 颗糖果的口味,所以小明可以在买之前就知道每包内的糖果口味。给定 N 包糖果,请你计算小明最少买几包,就可以品尝到所有口味的糖果。
输入描述
第一行包含三个整数 N,M,K。
接下来 N 行每行 K 个整数 T1,T2,⋅⋅⋅,TK,代表一包糖果的口味。
其中,对于30%的评测用例,1<N<20。对于所有评测样例,1<N<100,1≤M<20,1K <20,1≤Ti≤M。)
输出描述
输出一个整数表示答案。如果小明无法品尝所有口味,输出 −1。
输入输出样例
输入
6 5 3 1 1 2 1 2 3 1 1 3 2 3 5 5 4 2 5 1 2输出
2
暴力法
- 对n包糖果做任意组合,找到其中一种组合,能覆盖所有口味,并且需要的糖果包数量最少。
- n包糖果的组合共有
种,暴力法只能通过30%的测试。
- 再用set()对每一种组合进行去重,看看那种组合能否覆盖所有口味。
DP
(1)定义状态dp[i]:表示得到口味组合 i(有i种口味) 所需要的最少糖果包数量。(当i=M就是答案)
(2)状态转移。往口味组合i中加入一包糖果,得到新的口味组合j,说明从i到j需要糖果包数量dp[i]+1。若原来的dp[j]大于dp[i]+1,说明原来得到j的方法不如现在的方法,更新dp[j] = dp[i]+1。
关键问题:如何表示口味组合。
1、普通方法:为每一包糖果定义一个大小为m的数组(以表示m种口味),记录它的口味。n包糖果的口味是一个n*m的二维数组,定义为kw[n][m]。
- 例:设共有m=10种口味,kw[1][ ] ={0,0,0,0,0,1,0,1,1,0},表示第一包糖果的口味有三种。
2、状态压缩:记录一包糖果的口味,用二进制数表示。
- 例:一包里面有3颗糖果,分别是“2,3,5”三种口味,用一个二进制数“10110”表示,这个二进制数的每一位表示一种口味。
- 使用状态压缩之后,原来需要用二维数组kw[n][m]才能表示n包糖果的口味,现在只需要一个一维数组kw[n] 。
- 例如kw[1] = 10110,表示第一包的口味是“2,3,5”三种。
- 状态压缩DP的代码写起来很简洁,因为可以用位运算来简化代码。
1、用状态压缩表示糖果口味
例:输入一包糖果的“2,3,5”三种口味。
把这3个口味压缩成二进制数10110,做“移位 << ”和“或 | ”操作。
- (1)定义初始值tmp = 0。(初始口味为0)
- (2)输入口味“2”。
先移位1<<(2-1),得二进制数10;然后再与tmp或,得tmp = tmp | 10 = 10。
- (3)输入口味“3”。
先移位1<<(3-1),得二进制数100;然后再与tmp或,得tmp = tmp | 100 = 110。
- (4)输入口味“5”。
先移位1<<(5-1),得二进制数10000;然后再与tmp或,得tmp = tmp | 10000 = 10110。
代码:tmp |= (1<<x-1)
2、dp[ ]中状态压缩的处理
dp[i]:i 表示口味,用状态压缩表示; dp[i]表示得到口味i的最少糖果包数量。
状态转移:同样用到二进制的“或”操作。例如tmp表示某一包的糖果口味,那么dp[i | tmp]就表示得到口味 i | tmp所需要的最少糖果包数量。
代码:
n, m, k = map (int,input (). split())
tot = (1 <<m)-1 # tot:二进制是m个1,表示所有m种口味
dp = [-1 for _ in range(1 << 20)] # 初始化为-1,因为无解时输出-1
dp[0] = 0 # 初始化为0,代表0包糖果有0种口味
kw = []
for _ in range (n):kw.append([int(i) for i in input ().split()]) # kw是二维矩阵
for c in kw: # 按行遍历每包糖果tmp = 0for x in c: tmp |= (1 <<(x-1)) # 遍历这包糖果的口味for i in range(tot+1): # 遍历所有组合if (dp[i] == -1): continue # 不存在得到口味i的最少糖果包数量newcase = i | tmp # 加上新的一包后的新的口味组合if (dp[newcase] == -1) or (dp[newcase] > dp[i] +1): # 新的口味之前没算过或者包数比之前多dp[newcase] = dp[i] +1
print(dp[tot]) # 得到所有口味tot的最少糖果包数量
第二行代码解释:例如m=5,(1<<m)=100000 ,那么(1<<m)-1 = 11111,表示五种口味。
复杂度:for循环,tot=2m;for循环n次,总复杂度O(n2m),本题n=100,m=20,约为一亿次。
例题:矩阵计数
题目描述
一个 N×M 的方格矩阵,每一个方格中包含一个字符 O 或者字符 X。
要求矩阵中不存在连续一行 3 个 X 或者连续一列 3 个 X。
问这样的矩阵一共有多少种?
输入描述
输入一行包含两个整数 N,M (1≤N,M≤5)。
输出描述
输出一个整数代表答案。
输入输出样例
输入
2 3输出
49
思路:
- 很直接的状态压缩DP。
- 把方格中的字符‘0’看成数字0,字符‘X’看成数字1。
- 把每一行看成一个m位的二进制数,例如一行字符“OOXOX”对应二进制数“00101”。
- 一行数字有
种情况,即范围[0,1<<m)内的数字。这些数字里面只有部分数字符合要求,把这些数存进一个数组 row[ ]。
- 要求:这个数字中没有连续的3个1。一个符合要求的数就是这一行的一个合法状态。
做法
- 定义状态dp[i][i][k]:第i行的合法状态为j,前一行的合法状态为k时,符合条件的矩阵有多少个。(处理比较连续三行的定义方法)
- 连续3行的情况:设第i行状态为j,前一行状态为k,再前面一行状态为p,那么j & k& p等于0,说明这3行没有一列上是3个1。这3行是一种合法状态。
- 状态的递推:
if j & k & p==0:
dp[i][i][k] += dp[i- 1][k][p]
代码
check (x) :
检查一行(用x表示这一行)里面有没有连续的3个1
dp[ ][ ][ ]:定义三维的dp
dp[i][][k]:第i行的合法状态为j,前一行的合法状态为k时,符合条件的矩阵有多少个
def check(x): #检查x中有没有连续3个1num = 0while x:if x & 1:num += 1 # 从第一位开始,发现一个1else:num = 0 # 没有1则重置为0if num == 3: return False # 有连续3个1x >>= 1 #右移一次return True # 没有连续三个1,满足要求
N,M = list(map(int, input ().split()))
s = 2**M
row = [] # 合法的行
for i in range(s): # i的范围:00000~11111if check(i): row.append(i) # 加入合法的行
dp = [[[0 for i in range(s)] for j in range(s)] for k in range (N)] # 初始化dp
for i in row :dp[0][i][0]= 1 # 初始化第0行的符合条件的矩阵数均为1
# 遍历第1~N-1行,统计满足要求的矩阵数量
for i in range(1, N): # 1~N-1# 对每一行遍历合法行的情况下,再检查连续3列(当前一行和前两行)是否合法for j in row: for k in row:for p in row:if j & k & p == 0: # 连续三列不是三个1dp[i][j][k] += dp[i - 1][k][p]
ans = 0
for j in row :ans += sum(dp[N - 1][j]) # 对最后一行求和,其中sum(dp[N - 1][j])是求最后一行的第j中合法状态的和
print(ans)
复杂度:4个for循环m
例题:回路计数
题目描述
蓝桥学院由 21 栋教学楼组成,教学楼编号 1 到 21。对于两栋教学楼 a 和 b,当 a 和 b 互质时,a 和 b 之间有一条走廊直接相连,两个方向皆可通行,否则没有直接连接的走廊。
小蓝现在在第一栋教学楼,他想要访问每栋教学楼正好一次,最终回到第一栋教学楼(即走一条哈密尔顿回路),请问他有多少种不同的访问方案?
两个访问方案不同是指存在某个i,小蓝在两个访问方法中访问完教学楼 i 后访问了不同的教学楼。
提示:建议使用计算机编程解决问题。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
Hami lton问题
- Hamilton问题是NP问题,没有多项式复杂度的解法。
- 暴力解法:枚举n个点的全排列。共n!个全排列,一个全排列就是一条路径。本题n=21,21! = 51,090,942,171,709,440,000
- 用状态压缩DP,复杂度下降为
- 参考:《算法竞赛》341页,或者csdn搜“罗勇军”找到“状态压缩DP”
状态压缩DP
- 路径起点是1,绕一圈回到1。
- 问题转化:1先到2~21中的某个点,然后再绕一圈回到1。
- 定义DP。设S是图的一个子集,用dp[S][j]表示“集合S内的Hamilton路径个数”, 即从起点1出发经过 S中所有点 ,到达 终点j 时的路径个数。
- 最后求所有的访问方案:累加所有的dp[X][2]~dp[X][21]。其中X = 1 << 22 - 2(-2是两个-1,-1是改造21个1,-1是把起点1置为0),X是除了点1以外的所有其他点。
哈密尔顿问题与DP
- 如何求dp[S][ ]? 从小问题S-j递推到大问题S。S - j 表示从集合S中去掉j,即
不包含j点的集合。
- 如何从S-j递推到S? 设k是S-j中一个点,把从1到j的路径分为两部分: ( 1→...→k)+(k→j)。以k为变量枚举S-j中所有的点
- 状态转移方程: dp[S][j]+=dp[S-j][k]
- 代码:dp[S][j] += dp[S - (1<<j)][k]

代码:
初始化:
教学楼编号1到21。教学楼a和b,当a和b互质时,a和b之间有一条走廊直接相连,两个方向皆可通行,否则没有直接连接的走廊。
from math import gcdm = 1 << 22
dp = [[0 for j in range(22)] for i in range(m)]
dist = [[False for j in range(22)] for i in range(22)] # 记录联通关系
for i in range(1, 22):for j in range(1, 22):if gcd(i, j) == 1: # 最小公因数为1,互质dist[i][j] = True
dp[2][1] = 1 # 初始化dp
for S in range(2, m - 1): # 遍历所有集合Sfor j in range(1, 22): # 从21个抽一个j出来if S >> j & 1: # 集合S中包括jfor k in range(1, 22):if S - (1 << j) >> k & 1 and dist[k][j]: # 集合S-j包括k,且k和j联通dp[S][j] += dp[S - (1 << j)][k] # 累加S-j集合
ans = 0
for i in range(2, 22): ans += dp[m - 2][i]
print(ans)
# 881012367360
复杂度:3个for循环
m=221212=924,844,032,运行时间长达5分钟,所以这是一道填空题。
相关文章:
算法第十七期——状态规划(DP)之动态压缩
一、总述 状态压缩动态规划,就是我们俗称的状压DP,是利用计算机二进制的性质来描述状态的一种DP方式。 应用背景:以集合为状态,且集合可以用二进制来表示,用二进制的位运算来处理。集合问题一般是指数复杂度的&#x…...
网络安全竞赛试题A模块第八套解析(详细))
2022年全国职业院校技能大赛(中职组)网络安全竞赛试题A模块第八套解析(详细)
2022年全国职业院校技能大赛(中职组) 网络安全竞赛试题 (8) (总分100分) 赛题说明 一、竞赛项目简介 “网络安全”竞赛共分A.基础设施设置与安全加固;B.网络安全事件响应、数字取证调查和应用安全;C.CTF夺旗-攻击;D.CTF夺旗-防御等四个模块。根据比赛实际情况,竞…...

【华为OD机试真题 JAVA】数组中是否存在满足规则的数字组合
标题:数组中是否存在满足规则的数字组合 | 时间限制:1秒 | 内存限制:262144K | 语言限制:不限 给定一个正整数数组,检查数组中是否存在满足规则的数字组合 * 规则: * A = B + 2C 输入描述: * 第一行输出数组的元素个数。 * 接下来一行输出所有数组元素,用空格…...

【OpenCV技能树】——OpenCV基础
前言: 😊😊😊欢迎来到本博客😊😊😊 目前正在进行 OpenCV技能树的学习,OpenCV是学习图像处理理论知识比较好的一个途径,至少比看书本来得实在。本专栏文章主要记录学习Op…...

人体姿态识别
自留记录论文阅读,希望能了解我方向的邻域前沿吧 粗读,持续更新 第一篇 ATTEND TO WHO YOU ARE: SUPERVISING SELF-ATTENTION FOR KEYPOINT DETECTION AND INSTANCE-AWARE ASSOCIATION 翻译:https://editor.csdn.net/md?not_checkout=1&spm=1001.2014.3001.5352&…...

ubuntu下调试驱动
使用 Ubuntu Linux 测试 Linux 驱动 1. 测试 Linux 驱动准备工作 对于一个 Linux 驱动程序,一开始可以在 Ubuntu Linux 上做前期开发和测试。对于访问硬件部分也可以在 Ubuntu Linux 用软件进行模拟,切记不能代替真实的环境!当基本开发完成后&#…...
第十四届蓝桥杯三月真题刷题训练——第 9 天
第 1 题:找素数 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 素数就是不能再进行等分的整数。比如:7,11。而 9 不是素数,因为它可以平分为 3 等份。一般认为最小的…...

操作系统复习
熟练掌握操作系统的定义,操作系统的特征,操作系统的功能熟练掌握多道程序设计的概念,单道程序设计和多道程序设计的区别,多道程序设计的优点熟悉操作系统接口的主要功能,系统调用的基本概念、类型、实现。操作系统接口…...
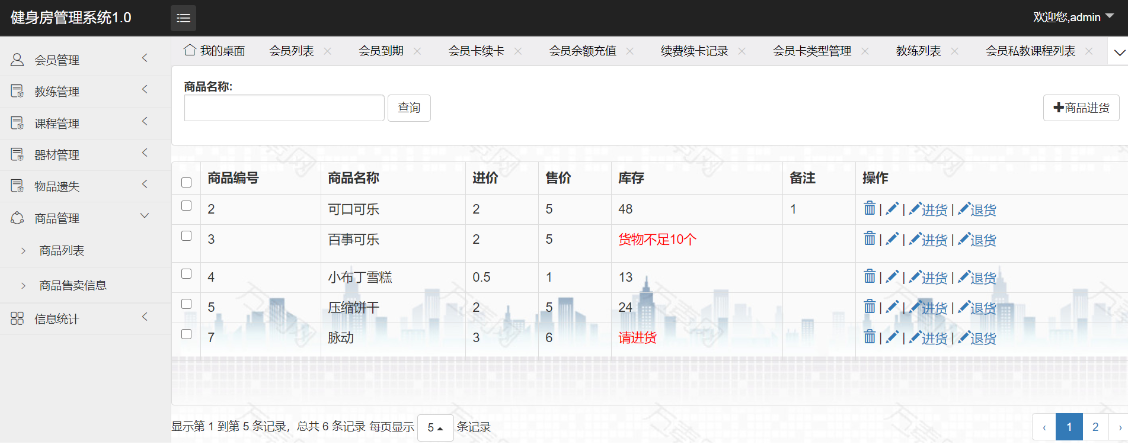
springboot健身房管理系统
springboot健身房管理系统 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍…...

C语言学习笔记——数组
前言 数组是C语言中的一种自定义数据类型,它的使用非常广泛。但是很多新手在使用数组时,经常在一些细节上出问题,导致程序崩溃或者无法编译。今天,我就来详细聊聊数组的使用和我注意到的一些细节。 一、常见的数组类型与数组的创建…...

类和对象 - 中
本文已收录至《C语言》专栏! 作者:ARMCSKGT 目录 前言 正文 构造函数 对比C和C的初始化 构造函数的使用与特性 默认构造函数 C11关于默认构造缺陷的补丁 析构函数 析构函数特性 默认析构和自定义析构 拷贝构造函数 问题聚焦 拷贝构造的定…...
Android之屏幕适配方案
在说明适配方案之前,我们需要对如下几个概念有所了解:屏幕尺寸,屏幕分辨率,屏幕像素密度。 屏幕尺寸 屏幕尺寸指屏幕的对角线的物理长度,单位是英寸,1英寸2.54厘米。 比如常见的屏幕尺寸:5.0、5…...

SpringBoot+jersey跨域文件上传
一、配置tomcat服务器 1.1、添加upload文件夹 在webapps\Root文件夹下创建用于接收上传文件的upload文件夹 1.2、修改conf\web.xml设置允许上传文件 <init-param><param-name>readonly</param-name><param-value>false</param-value></ini…...

数据结构One——绪论
本喵是FW视频封面最终版宝子,你不点个赞吗?不评个论吗?不收个藏吗? 最后的最后,关注我,关注我,关注我,你会看到更多有趣的博客哦!!! 喵喵喵&#…...
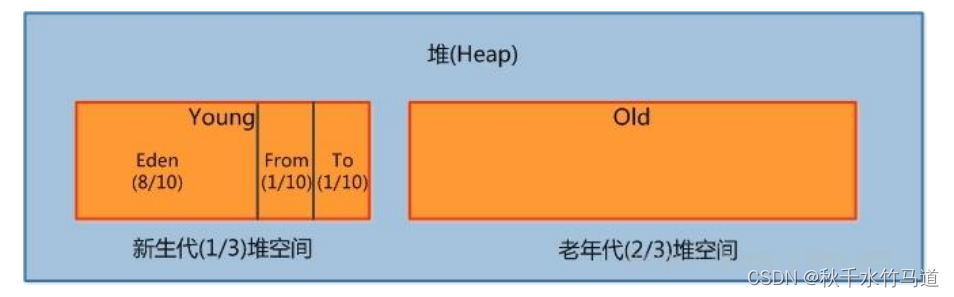
JVM篇之内存及GC
目录一、JVM内存区域1.1程序计数器1.2虚拟机栈1.3本地方法栈1.4堆1.5方法区二、JVM运行时内存2.1新生代(轻量级GC)2.2老年代(重量级GC)一、JVM内存区域 JVM 内存区域主要分为线程私有区域【程序计数器、虚拟机栈、本地方法栈】、线程共享区域【JAVA 堆、…...
的一些方式)
Linux驱动操作地址(寄存器)的一些方式
Linux驱动操作地址(寄存器)的一些方式 文章目录Linux驱动操作地址(寄存器)的一些方式1.对绝对地址赋值操作2. ioremap2.1 void __iomem *地址2.2 volatile unsigned int *地址2.3 structioremap1.对绝对地址赋值操作 对绝对地址0x100000赋值操作 *&…...

Java日志框架介绍
Log4j Apache Log4j是一个基于Java的日志记录工具。它是由Ceki Glc首创的,现在则是Apache软件基金会的一个项目。 Log4j是几种Java日志框架之一。 Log4j 2 Apache Log4j 2是apache开发的一款Log4j的升级产品。 Commons Logging Apache基金会所属的项目,是…...

编程中遇到的计算机大小端概念
概念大小端(Endian)是指在一个多字节的数据中,字节的存储顺序的规定。通俗来说,就是指数据在计算机内部存储时的顺序问题。在计算机系统中,一个数据项可能占据多个存储单元。在这种情况下,这个数据项的存储…...
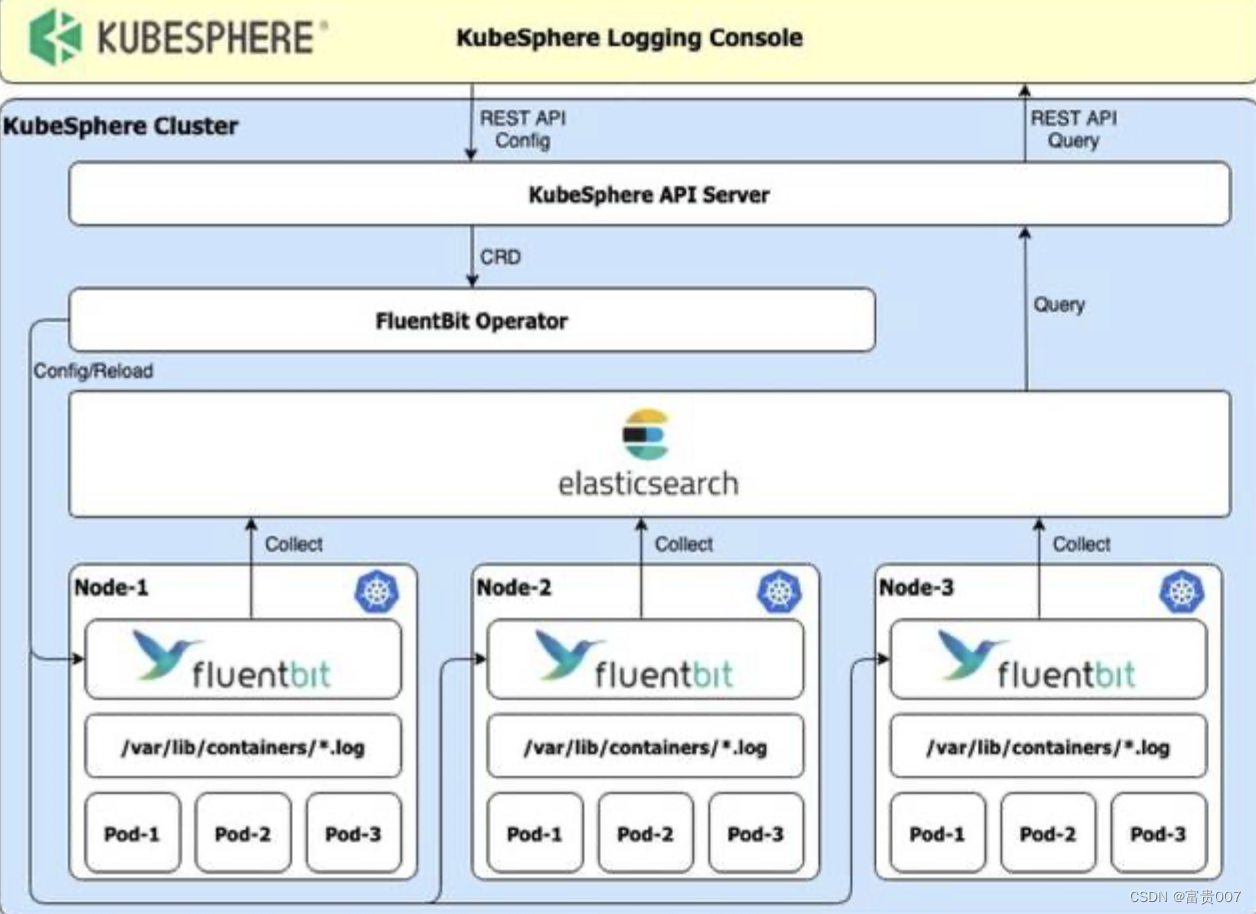
日志与可视化方案:从ELK到EFK,再到ClickHouse
EFK方案 从ELK谈起 ELK是三个开源软件的缩写,分别表示:Elasticsearch,Logstash,Kibana。新增了一个FlieBeat,它是一个轻量级的日志收集处理工具,FlieBeat占用资源少,适用于在各个服务器上搜集…...

字符函数和字符串函数(上)——“C”
各位CSDN的uu们你们好呀,今天小雅兰来给大家介绍一个全新的知识点,就是字符函数和字符串函数啦,其实其中有些函数我之前已经学习过了,比如strlen、strcpy;也有一些之前不是很熟悉的函数,比如strstr、strtok…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
