JavaScript(6)——数据类型转换
为什么需要类型转换?
JavaScript是弱数据类型:JavaScript不知道变量到底属于哪种数据类型,只有赋值了才清除
使用表单,prompt获取的数据默认为字符串类型,此时不能直接进行算数运算
隐式转换
某些运算符被执行时,系统内部自动将数据类型进行转换,这种转换被称为隐式转换。
规则:
+号两边只要有一个字符串,都会把另一个转换为字符串
除了+以外的算数运算符,比如-*/等都会将数据转换为数字类型
显式转换
隐式转换规律并不清晰,大多是靠经验总结的规律,为了避免因隐式转换带来的问题,通常根逻辑需要对数据进行显示转换。
转换为数字型
- Number(数据)
如果字符串内容里面有非数字,转换失败结果为NaN
NaN也是number类型的数据,代表非数字
- parselnt(数据)
只保留整数
- paresFloat(数据)
可以保留小数
let str = '123'let a = '123.12'let b = '321.32'console.log(Number(str))console.log(parseInt(a))console.log(parseFloat(b))console.log(parseInt('html'))console.log(parseFloat('12.12px')) 
当里面的数据是数字+字符时,转换结果为前面的数字,但不能中间插入字符
console.log(Number('pp129.1p2pxaaa'))console.log(parseFloat('12.32pp'))console.log(Number('22p.2'))
相关文章:

JavaScript(6)——数据类型转换
为什么需要类型转换? JavaScript是弱数据类型:JavaScript不知道变量到底属于哪种数据类型,只有赋值了才清除 使用表单,prompt获取的数据默认为字符串类型,此时不能直接进行算数运算 隐式转换 某些运算符被执行时&am…...

概率论与数理统计_下_科学出版社
contents 前言第5章 大数定律与中心极限定理独立同分布中心极限定理 第6章 数理统计的基本概念6.1 总体与样本6.2 经验分布与频率直方图6.3 统计量6.4 正态总体抽样分布定理6.4.1 卡方分布、t 分布、F 分布6.4.2 正态总体抽样分布基本定理 第7章 参数估计7.1 点估计7.1.1 矩估计…...

Android 复习layer-list使用
<shape android:shape"rectangle"> <size android:width"1dp" android:height"100px" /> <solid android:color"#FFFFFF" /> </shape> 通过shape画线段,通过 <item android:gravity"left|top"…...

汉光联创HGLM2200N黑白激光多功能一体机加粉及常见问题处理
基本参数: 机器型号:HGLM2200N 产品名称:A4黑白激光多功能一体机 基础功能:打印、扫描、复印 打印速度:22页/分钟 纸张输入容量:150-249页 单面支持纸张尺寸:A4、A5、A6 产品尺寸&#x…...

引领汽车软件开发走向ASPICE认证之路
亚远景科技与ASPICE认证的关系可以从以下几个方面来阐述: (要明确的是:在ASPICE行业中专业来说,ASPICE项目是没有认证,而只有评估。不过,为了方便沟通,人们常将这一评估过程称为认证。) 行业专…...

【C/C++ new/delete和malloc/free的异同及原理】
new/delete和malloc/free都是用于在C(以及C语言在malloc/free的情况下)中动态申请和释放内存的机制,但它们之间存在一些显著的异同点。以下是对这两组函数/运算符的异同点的详细分析: 相同点 目的相同:两者都用于在堆…...

Maven Archetype 自定义项目模板:高效开发的最佳实践
文章目录 前言一、Maven Archetype二、创建自定义 Maven Archetype三、定制 Archetype 模板四、手动创建 Archetype 模板项目五、FAQ5.1 如何删除自定义的模板5.2 是否可以在模板中使用空文件夹 六、小结推荐阅读 前言 在软件开发中,标准化和快速初始化项目结构能够…...

vue的ESLint 4格缩进 笔记
https://chatgpt.com/share/738c8560-5271-45c4-9de0-511fad862109 一,代码4格缩进设置 .eslintrc.js文件 module.exports { "rules": { "indent": ["error", 4] } }; 自动修复命令 npx eslint --fix "src/**/*.{…...
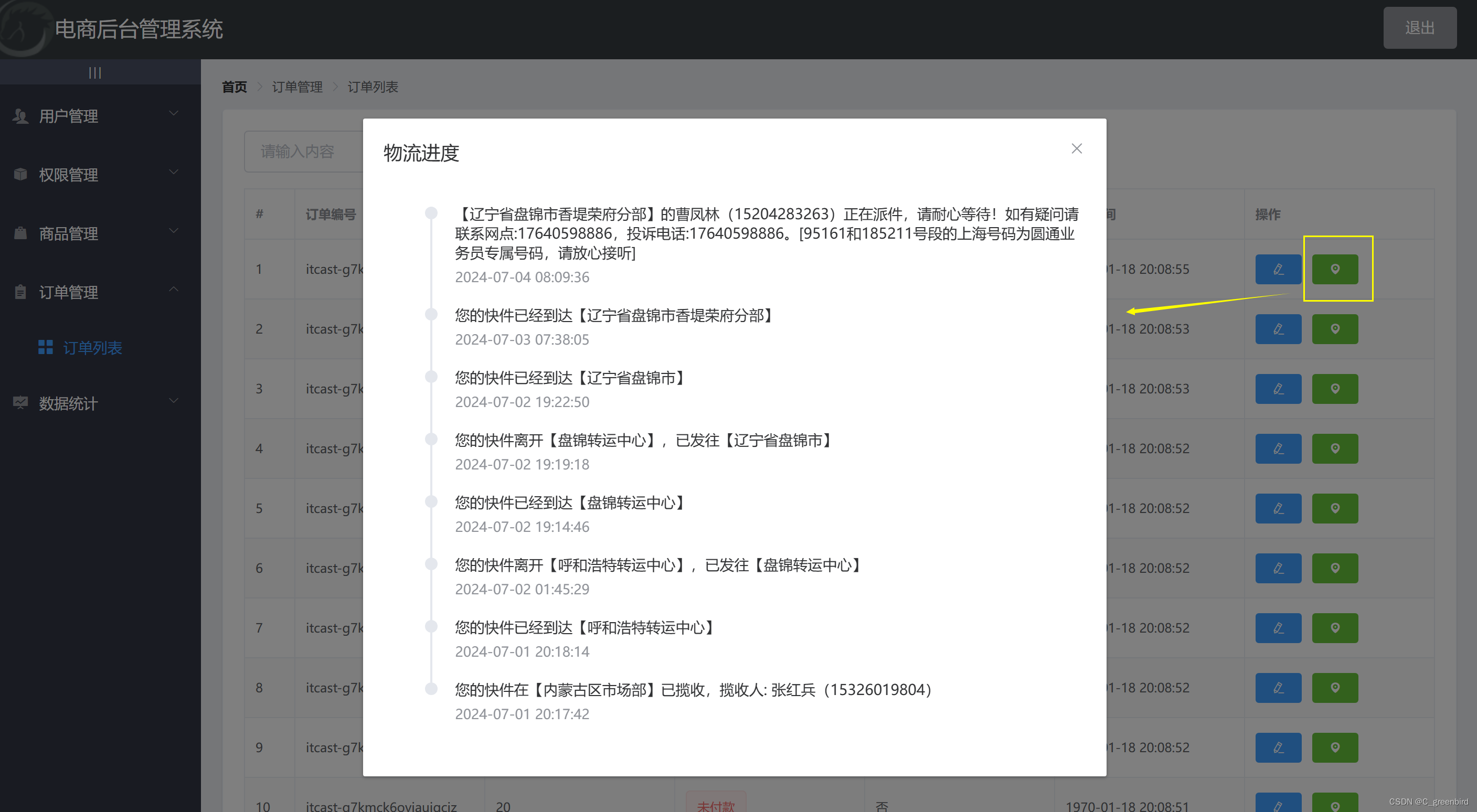
【前端项目笔记】8 订单管理
订单管理 效果展示: 在开发功能之前先创建分支order cls 清屏 git branch 查看所有分支(*代表当前分支) git checkout -b order 新建分支order git push -u origin order 将本地的当前分支提交到云端仓库origin中命名为order 通过路由方式…...

构建Yarn依赖树:深入解析与实践指南
构建Yarn依赖树:深入解析与实践指南 在现代JavaScript开发中,依赖管理是项目成功的关键。Yarn,作为Node.js生态系统中一个强大的包管理器,以其快速、可靠和安全的特性而闻名。本文将深入探讨Yarn如何构建依赖树,并提供…...

社区活动|FlowUs知识库的发展|先进技术的落地应用|下一代生产力工具你用了吗
在当今快速发展的数字化时代,技术的进步不断推动着工作方式和知识管理的革新。FlowUs,作为一款前沿的知识管理和协作平台,正站在这一变革的浪潮之巅,引领着智能工作的新潮流。 智能化的智能学习引导工具 FlowUs不仅仅是一个工具&…...

Python基础语法(与C++对比)(持续更新ing)
代码块 Python在统一缩进体系内,为同一代码块C{...}内部的为同一代码块 注释 Python 单行注释:#... 多行注释:... C 单行注释://... 多行注释: /*...*/ 数据类型 1. Python数据类型 Python中支持数字之间使用下划线 _ 分割…...

LeetCode-Leetcode 1120:子树的最大平均值
LeetCode-Leetcode 1120:子树的最大平均值 题目描述:解题思路一:递归解题思路二:0解题思路三:0 题目描述: 给你一棵二叉树的根节点 root,找出这棵树的 每一棵 子树的 平均值 中的 最大 值。 子…...

AI在软件开发中的角色:助手还是取代者?
目录 前言 一、AI工具现状:高效助手的崛起 二、AI对开发者的影响:新技能与竞争力的重塑 三、AI开发的未来:共生而非取代 写在最后 前言 随着科技的飞速发展,生成式人工智能(AIGC)在软件开发领域的应用日…...

jboss 7.2
链接: https://pan.baidu.com/s/19PSAy-Wy8DjcUMy94eqWnw 提取码: rgxf 复制这段内容后打开百度网盘手机App,操作更方便哦 --来自百度网盘超级会员v3的分享链接: https://pan.baidu.com/s/19PSAy-Wy8DjcUMy94eqWnw 提取码: rgxf 复制这段内容后打开百度网盘手机App…...
鸿蒙开发:Universal Keystore Kit(密钥管理服务)【密钥生成介绍及算法规格】
密钥生成介绍及算法规格 当业务需要使用HUKS生成随机密钥,并由HUKS进行安全保存时,可以调用HUKS的接口生成密钥。 注意: 密钥别名中禁止包含个人数据等敏感信息。 开发前请熟悉鸿蒙开发指导文档:gitee.com/li-shizhen-skin/harm…...

电气-伺服(4)CANopen
一、CAN Controller Area Network ,控制器局域网,80年的德国Bosch的一家公司研发可以测量仪器直接的实时数据交换而开发的一款串行通信协议。 CAN发展历史 二、CAN 的osi 模型 CAN特性: CAN 的数据帧 三、CANopen 什么是CANopen CANopen 的网络模型 …...

JavaFx基础知识
1.Stage 舞台 如此这样的一个框框,舞台只是这个框框,并不管里面的内容 public void start(Stage primaryStage) throws Exception {primaryStage.setScene(new Scene(new Group()));primaryStage.getIcons().add(new Image("/icon/img.png"))…...
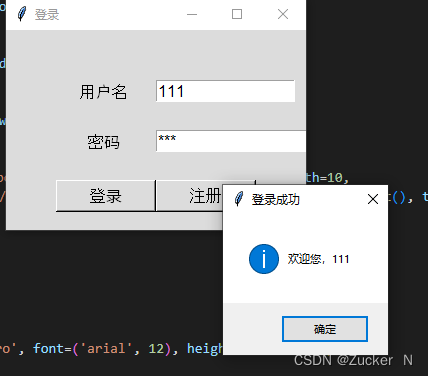
学会python——用python制作一个登录和注册窗口(python实例十八)
目录 1.认识Python 2.环境与工具 2.1 python环境 2.2 Visual Studio Code编译 3.登录和注册窗口 3.1 代码构思 3.2 代码实例 3.3 运行结果 4.总结 1.认识Python Python 是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。 Python 的设计具有很强的可读…...

Vue3+Element-plus的表单重置
作用:简化代码,重置表单数据 1.创建表单,绑定表单数据对象model,并且每一表单需要绑定prop <el-button type"primary" click"Formreset">重置</el-button> <el-form :inline"true" :model"fromModel" ref"form&q…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
