MATLAB——FFT(快速傅里叶变换)
基础知识
FFT即快速傅里叶变换,利用周期性和可约性,减少了DFT的运算量。常见的有按时间抽取的基2算法(DIT-FFT)按频率抽取的基2算法(DIF-FFT)。
1.利用自带函数fft进行快速傅里叶变换
若已知序列x=[4,3,2,6,7,8,9,0]x=[4,3,2,6,7,8,9,0]x=[4,3,2,6,7,8,9,0],求X(k)=DFT[x(n)]X(k)=DFT[x(n)]X(k)=DFT[x(n)]
代码非常简单,只有两行
x=[4,3,2,6,7,8,9,0];
xk=fft(x)

一般,对MATLAB而言,要想让它显示出结果,计算的部分不要加分号。
2.绘制128点DFT的幅频图
已知信号由15Hz幅值0.5的正弦信号和40Hz幅值2的正弦信号组成,数据采样频率为100Hz,试绘制N=128点DFT的幅频图。
关于下列代码的解释
f=(0:N-1)'*fs/N;
其中(0:N-1)'是生成了一个长度为N,间隔为1的列向量转置所得到的行向量。fs/N是指频域上的频率间隔。
若N点序列x(n)(n=0,1,…,N-1)是在采样频率fs(Hz)下获得的。它的FFT也是N点序列,即X(k)(k=0,1,…,N-1),则第K点对应实际频率值为:
f=k*fs/N
clc;
fs=100;
Ts=1/fs;%采样时间间隔
N=128;
n=0:N-1;
t=n*Ts; %x不是直接关于n的函数,因为是固定的采样时间点
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);y=fft(x,N);
f=(0:N-1)'*fs/N;
stem(f,abs(y));
运行结果
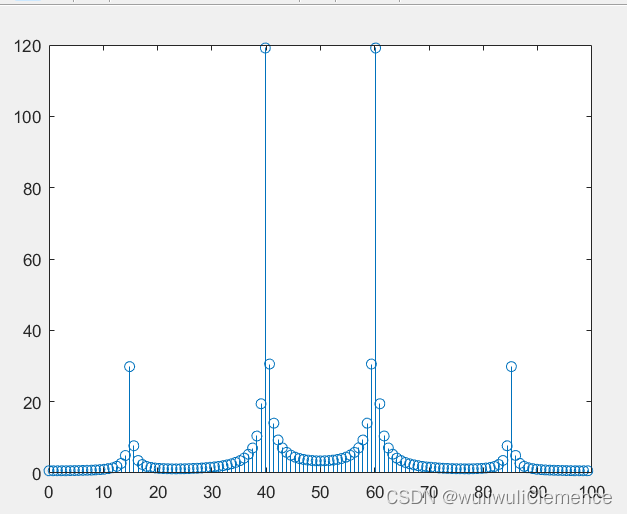
同时也可以可看到这个幅度谱是关于fN对称的。
3.利用FFT进行功率谱的噪声分析
已知带有测量噪声信号x(t)=sin(2πf1t)+sin(2πf2t)+2w(t)x(t)=sin(2πf1t)+sin(2πf2t)+2w(t)x(t)=sin(2πf1t)+sin(2πf2t)+2w(t) 其中f1=50Hz,f2=120Hz, w(t)为均值为零、方差为1的随机信号,采样频率为1000Hz,数据点数N=512。试绘制信号的功率谱图。
下面先介绍几个基本的函数和知识:
conj(Y)
conj(Y) 是 MATLAB 中的一个函数,表示对 Y 中的每个元素取其共轭复数。如果 Y 是一个实数数组,则返回其本身。在信号处理中,常常使用共轭复数进行频域变换的处理。
求功率
P=Y.*conj(Y)/512;
注意这里是点乘啊。
在信号处理中,功率可以表示为信号的平均能量。对于一个离散时间信号,其能量可以表示为其幅度平方的总和,即:
E=∑n=0N−1∣x[n]∣2E = \sum_{n=0}^{N-1} |x[n]|^2 E=n=0∑N−1∣x[n]∣2
其中,NNN 是信号的抽样点数,x[n]x[n]x[n] 是信号在时刻 nnn 的采样值。这里的 ∣x[n]∣2|x[n]|^2∣x[n]∣2 表示对 x[n]x[n]x[n] 取模长平方。
如果要计算信号的平均功率,可以将其总能量除以抽样点数,即:
P=EN=1N∑n=0N−1∣x[n]∣2P = \frac{E}{N} = \frac{1}{N} \sum_{n=0}^{N-1} |x[n]|^2 P=NE=N1n=0∑N−1∣x[n]∣2
这里的 PPP 表示信号的功率。
在代码中,YYY 表示信号的离散傅里叶变换,即频域表示,其幅度 ∣Y∣|Y|∣Y∣ 表示信号在每个频率分量上的贡献。为了计算信号的功率谱,需要将 YYY 变换为其幅度平方,即 ∣Y∣2|Y|^2∣Y∣2。由于 YYY 中包含了正频率和负频率的信息,因此需要对其进行共轭操作,即将负频率部分取共轭复数,然后再与正频率部分相乘,即 Y⋅conj(Y)Y \cdot \operatorname{conj}(Y)Y⋅conj(Y)。最后将结果除以抽样点数 NNN,即可得到功率谱 PPP:
P=Y⋅conj(Y)NP = \frac{Y \cdot \operatorname{conj}(Y)}{N} P=NY⋅conj(Y)
这里的 PPP 是一个长度为 NNN 的向量,表示信号在每个频率分量上的功率。
randn
andn是MATLAB中的一个函数,用于生成一个均值为0,方差为1的标准正态分布随机数。例如,可以使用以下代码生成一个大小为3x3的标准正态分布随机矩阵:
A = randn(3,3);
完整代码
clc;
t=0:0.001:0.6;%设置步进与时间区间
x=sin(2*pi*50*t)+sin(2*pi*120*t);%根据已知写出信号的表达式
noise=randn(1,length(t));%生成均值为零、方差为1的随机信号,也就是噪声
y=x+noise;%带有噪声的信号
subplot(121);
plot(t,y);fs=1000;
Y=fft(y,512);%512点的FFT
P=Y.*conj(Y)/512;%求功率
f=(0:255)*fs/256%由上面的分析可知,频谱关于奈奎斯特频率对称,所以取其中一半
subplot(122);
plot(f,P(1:256))%功率随频率的变化,即功率谱图,绘制出一半
运行结果:
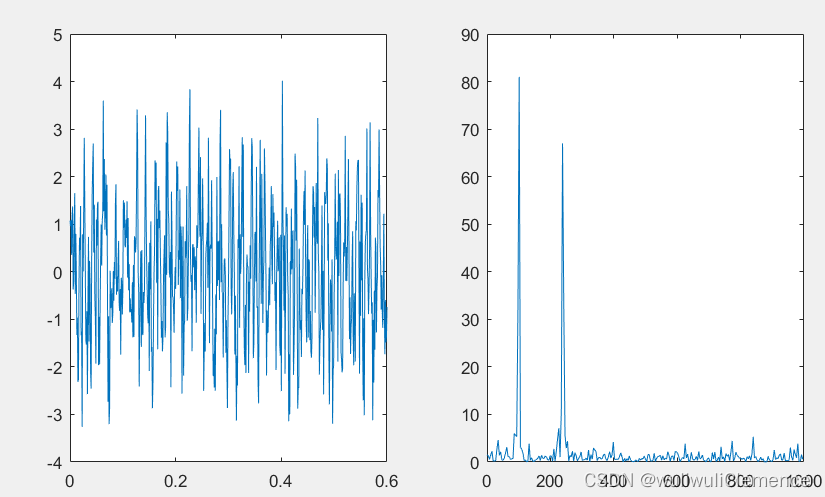
4.序列长度和FFT的长度对信号频谱的影响
已知信号 x(t)=0.5sin(2πf1t)+2sin(2πf2t)x(t)=0.5sin(2πf1t)+2sin(2πf2t)x(t)=0.5sin(2πf1t)+2sin(2πf2t)
其中f1=15Hz,f2=40Hz,采样频率为100Hz.
在下列情况下绘制其幅频谱。
有了前面的基础,这里就比较简单了
代码
nlength=32;
nfft1=32;
nfft2=128;
fs=100;
Ts=1/fs;
n=0:nlength-1;
t=n*Ts;x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);y1=fft(x,nfft1);
f1=(0:31)*fs/32;
subplot(211);
Y1=abs(y1);
plot(f1(1:16),Y1(1:16));y2=fft(x,nfft2);
f2=(0:127)*fs/128;
subplot(212);
Y2=abs(y2);
plot(f2(1:64),Y2(1:64));
运行结果
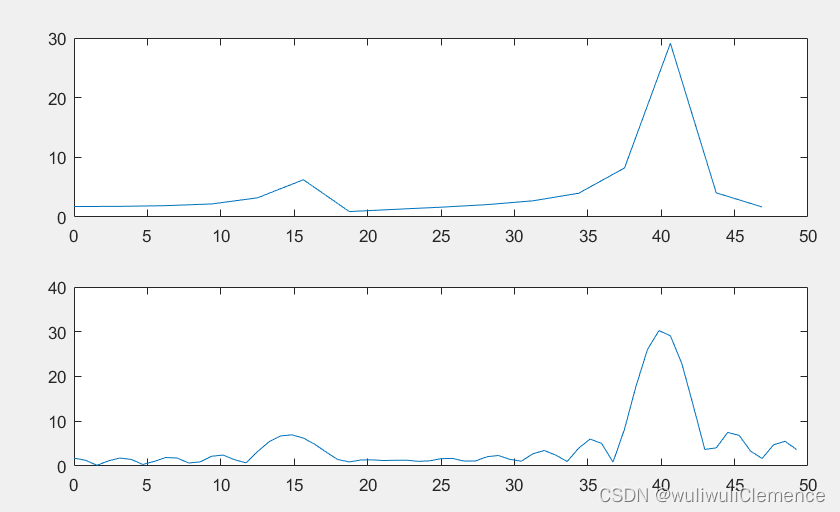
结果分析
采样点数越多,其频谱越光滑。
注意
绘制图形的时候,一定要分析清楚是频谱图,还是某一个变换,其目的在于分清谁是因变量,谁是自变量。
相关文章:

MATLAB——FFT(快速傅里叶变换)
基础知识 FFT即快速傅里叶变换,利用周期性和可约性,减少了DFT的运算量。常见的有按时间抽取的基2算法(DIT-FFT)按频率抽取的基2算法(DIF-FFT)。 1.利用自带函数fft进行快速傅里叶变换 若已知序列x[4,3,2,6…...

力扣-进店却未进行过交易的顾客
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1581. 进店却未进行过交易的顾客二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行…...
一文解决vscode中借助CMake配置使用Opencv过程中的所有问题
vscode中借助CMake配置使用opencv过程中的问题 vscode编译工程的完整过程 编写好CMakeLists.txtvscode中 ctrlshiftp 选择cmake configurevscode中 ctrlshiftp 选择cmake build CMake问题 1. set OpenCV_FOUND to FALSE so package “OpenCV” is considered to be NOT FOU…...

Golang每日一练(leetDay0004)
10. 正则表达式匹配 Regular Expression Matching 给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 . 和 * 的正则表达式匹配。 . 匹配任意单个字符* 匹配零个或多个前面的那一个元素 所谓匹配,是要涵盖 整个 字符串 s的,而不是部分…...

手机忘记密码解锁的 6 大软件方法
您可能想要解锁手机的原因有很多。也许您正在海外旅行并想使用当地的 SIM 卡,或者您可能刚买了一部二手手机并且需要删除之前所有者的个人数据。您可能想知道如何获得可以免费解锁任何手机的软件。Android 用户可以使用他们的指纹、面部识别或 PIN。您也可以通过快速…...

MySQL数据库的基础语法总结(1)
MySql一.数据库,数据表的基本操作1.数据库的基本操作2. 数据表的基本操作2.1 数据库的数据类型2.1.1 整数类型2.1.2 浮点数类型和定点数类型2.1.3 字符串类型2.1.4 日期与时间类型2.2 数据表的基本操作2.2.1 创建一个数据表2.2.2 查看数据表2.2.3 查看表的基本信息的MySQL指令2…...

Linux之进程创建
本节目录1.fork函数初识2.fork函数返回值3.写时拷贝1.fork函数初识 在Linux中,fork函数是一个非常重要的函数,它从已存在的进程中创建一个新进程。新进程叫做子进程,而原进程叫做父进程。 #include <unistd.h> pid_t fork(void); 返回…...

DCL 管理用户与权限控制
目录 DCL 查询用户 案例 权限控制 案例 DCL DCL英文全称是Data Control Language(数据控制语言),用来管理数据库用户、控制数据库的访问权限。 查询用户 1、查询用户 select * from mysql.user; 2、创建用户 CREATE USER 用户名主机名 IDENTIFIED BY 密码;…...
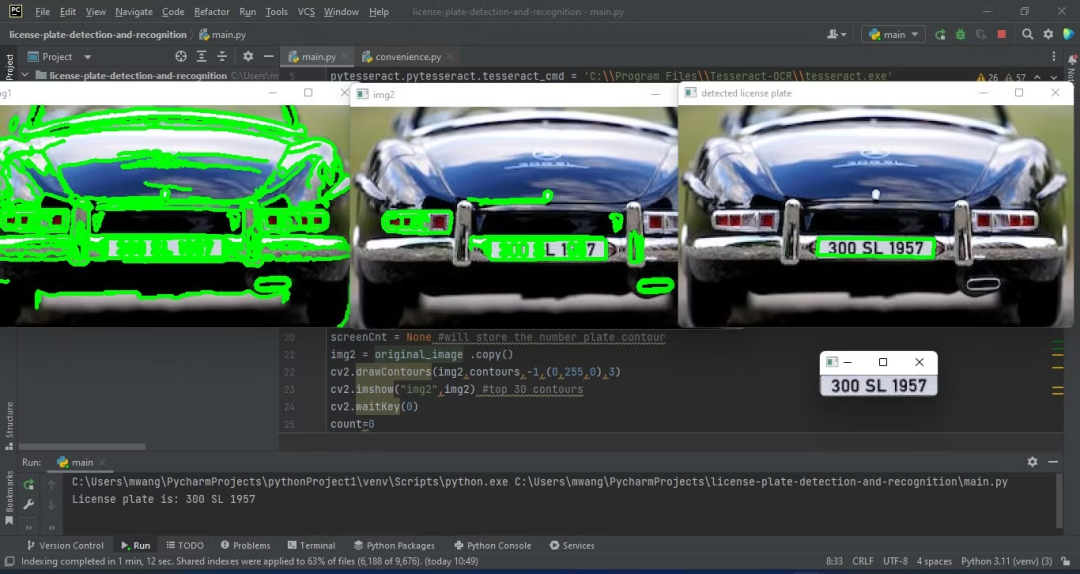
如何使用 Python 检测和识别车牌(附 Python 代码)
文章目录创建Python环境如何在您的计算机上安装Tesseract OCR?技术提升磨砺您的Python技能车牌检测与识别技术用途广泛,可以用于道路系统、无票停车场、车辆门禁等。这项技术结合了计算机视觉和人工智能。 本文将使用Python创建一个车牌检测和识别程序。…...

[Python题解] CodeForces 1804 D. Accommodation
✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。 🍎个人主页:小嗷犬的个人主页 🍊个人网站:小嗷犬的技术小站 🥭个人信条:为天地立心&…...

【设计模式】访问者模式
访问者模式 访问者模式被称为是最复杂的设计模式,比较难理解并且使用频率不高。 在 GoF 的《设计模式》⼀书中,访问者者模式(Visitor Design Pattern)是这么定义的: Allows for one or more operation to be applied to a set o…...

蓝桥杯刷题冲刺 | 倒计时27天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.递增序列2.等差素数列3.七段码4.亲戚5.连通块中点的数量1.递增序列 题目 链接:&am…...

RV1126_python人脸识别Retinaface+MobilefaceNet
RV1126_python人脸识别Retinaface+MobilefaceNet RV1126 具备RKNN 模块支持大部分如Pytorch、MXNet、Caffe、tensorflow、keras、onnx等常见框架,而且量化部署使用RKNN-toolkit非常方便。以下介绍通过RV1126实现的人脸识别过程。 首先人脸识别需要先做人脸检测>>人脸校正…...

HBase---HBase基础语法
HBase基础语法 文章目录HBase基础语法基本操作进入 HBase 客户端命令行查看命名空间查看命名空间下的表创建命名空间创建表查看表描述禁用/启用删除表新增列族删除列族更改列族存储版本的限制put 增加数据get 查看数据get条件查询删除指定列族下的指定列删除指定行全表扫描全表…...

2023年,PMP有多少含金量呢?
其实围绕以PMP含金量为中心的这个类似的小问题我好像也已经写了不少文章了。首先我肯定PMP的含金量,不管有多少质疑,这的确是事实。因为就是看中了他的价值考的,并且在项目的执行上收获了很多。 具体的可以看我接下来谈的PMP的价值&#x…...

vue动态路由
import Vue from vue import Router from vue-router import layout from ../components/layout Vue.use(Router) // 动态路由 export const asyncRouterMap = [ { path: /home, component: layout, name: home, meta: { title: 首页, icon: el-ic…...

被骗进一个很隐蔽的外包公司,入职一个月才发现,已经有了社保记录,简历污了,以后面试有影响吗?...
职场的套路防不胜防,一不留神就会掉坑,一位网友就被“骗”进了外包公司,他说公司非常隐蔽,入职一个月才发现是外包,但已经有了社保记录,简历污了,不知道对以后面试有影响吗?楼主说&a…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 -租车骑绿岛(Java) | 机试题+算法思路+考点+代码解析 【2023】
租车骑绿岛 题目 部门组织绿岛骑行团建活动。租用公共双人自行车骑行,每辆自行车最多坐两人、做大载重M。 给出部门每个人的体重,请问最多需要租用多少双人自行车。 输入 第一行两个数字m、n,自行车限重m,代表部门总人数n。 第二行,n个数字,代表每个人的体重。体重都…...

【Java|基础篇】用思维导图理解逻辑控制
文章目录顺序结构分支结构if单分支语句if else双分支语句if else if else多分支语句switch语句循环语句for循环while循环do while循环continuebreak总结顺序结构 顺序结构是指代码按照从上往下的顺序依次执行 分支结构 选择语句是条件成立时,才会执行的语句.共有三种.分为是if…...
Go单元测试基础
Go单元测试基础1.go test工具2.单元测试函数3.go test -v/go test -run4.跳过某些测试用例5.子测试6.表格驱动测试7.并行测试8.使用工具生成测试代码9.测试覆盖率1.go test工具 Go语言中的测试依赖go test命令。编写测试代码和编写普通的Go代码过程是类似的,并不需…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
