相关分析 - 肯德尔系数
肯德尔系数(Kendall’s Tau)是一种非参数统计方法,用于衡量两个变量之间的相关性。它是由统计学家莫里斯·肯德尔(Maurice Kendall)在1938年提出的。肯德尔系数特别适用于有序数据,可以用来评估两个有序变量之间的单调关系。
文章目录
- 肯德尔系数的定义
- 肯德尔系数的解释
- 肯德尔系数的计算步骤
- 肯德尔系数的优点和缺点
- 应用场景
- python 实现
- 解释
- 自定义实现
肯德尔系数的定义
肯德尔系数 τ \tau τ 的计算基于配对比较的概念。假设有两个变量 X X X 和 Y Y Y,每个变量有 n n n 个观测值。肯德尔系数 τ \tau τ 的定义如下:
τ = C − D n ( n − 1 ) 2 \tau = \frac{C - D}{\frac{n(n-1)}{2}} τ=2n(n−1)C−D
其中:
- C C C 是和谐配对的数量,即在 X X X 和 Y Y Y 中同时增加或减少的配对数量。
- D D D 是不和谐配对的数量,即在 X X X 和 Y Y Y 中一个增加另一个减少的配对数量。
- n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1) 是所有可能的配对数量。
肯德尔系数的解释
肯德尔系数 τ \tau τ 的取值范围在 -1 到 1 之间:
- τ = 1 \tau = 1 τ=1 表示完全正相关,即所有配对都是和谐的。
- τ = − 1 \tau = -1 τ=−1 表示完全负相关,即所有配对都是不和谐的。
- τ = 0 \tau = 0 τ=0 表示没有相关性,即和谐配对和不和谐配对的数量相等。
肯德尔系数的计算步骤
- 列出所有配对:对于 n n n 个观测值,列出所有可能的配对。
- 比较配对:对于每一对 ( X i , Y i ) (X_i, Y_i) (Xi,Yi) 和 ( X j , Y j ) (X_j, Y_j) (Xj,Yj),判断是和谐的还是不和谐的。
- 计算和谐和不和谐配对的数量:统计和谐配对和不和谐配对的数量。
- 计算肯德尔系数:使用上述公式计算肯德尔系数 τ \tau τ。
肯德尔系数的优点和缺点
优点:
- 适用于有序数据:肯德尔系数特别适用于有序数据,能够捕捉变量之间的单调关系。
- 不受异常值影响:肯德尔系数对异常值不敏感,因此在存在异常值的情况下比皮尔逊相关系数更稳健。
缺点:
- 计算复杂度:对于大数据集,计算所有配对的复杂度较高。
- 解释性:肯德尔系数的解释不如皮尔逊相关系数直观。
应用场景
肯德尔系数常用于社会科学、生物学、心理学等领域的研究中,特别是在需要评估两个有序变量之间关系的情况下。例如,在心理学研究中,可以使用肯德尔系数来评估两个评分者对同一组被试的评分一致性。
python 实现
首先,确保已经安装了scipy库。如果没有安装,可以使用以下命令进行安装:
pip install scipy
然后,可以使用以下代码来计算肯德尔系数:
import scipy.stats as stats# 示例数据
x = [1, 2, 3, 4, 5]
y = [1, 3, 2, 5, 4]# 计算肯德尔系数
tau, p_value = stats.kendalltau(x, y)print(f"肯德尔系数 (tau): {tau}")
print(f"p值: {p_value}")
在这个示例中,定义了两个有序变量x和y,然后使用stats.kendalltau函数来计算之间的肯德尔系数和对应的p值。
解释
tau:肯德尔系数,表示两个变量之间的相关性。p_value:p值,用于检验肯德尔系数是否显著。通常,如果p值小于0.05,则认为肯德尔系数是显著的。
自定义实现
如果想要自己实现肯德尔系数的计算,可以按照以下步骤进行:
def kendall_tau(x, y):n = len(x)if n != len(y):raise ValueError("x and y must have the same length")concordant = 0discordant = 0for i in range(n):for j in range(i + 1, n):if (x[i] < x[j] and y[i] < y[j]) or (x[i] > x[j] and y[i] > y[j]):concordant += 1elif (x[i] < x[j] and y[i] > y[j]) or (x[i] > x[j] and y[i] < y[j]):discordant += 1tau = (concordant - discordant) / (0.5 * n * (n - 1))return tau# 示例数据
x = [1, 2, 3, 4, 5]
y = [1, 3, 2, 5, 4]# 计算肯德尔系数
tau = kendall_tau(x, y)
print(f"肯德尔系数 (tau): {tau}")
在这个自定义实现中,定义了一个kendall_tau函数,该函数计算两个列表x和y之间的肯德尔系数。函数首先检查两个列表的长度是否相同,然后计算和谐配对和不和谐配对的数量,最后计算肯德尔系数。
相关文章:

相关分析 - 肯德尔系数
肯德尔系数(Kendall’s Tau)是一种非参数统计方法,用于衡量两个变量之间的相关性。它是由统计学家莫里斯肯德尔(Maurice Kendall)在1938年提出的。肯德尔系数特别适用于有序数据,可以用来评估两个有序变量之…...

【咨询】企业数字档案馆(室)建设方案-模版范例
导读:本模版来源某国有大型医药行业集团企业数字档案馆(室)建设方案(一期300W、二期250W),本人作为方案的主要参与者,总结其中要点给大家参考。 目录 1、一级提纲总览 2、项目概述 3、总体规…...

selfClass 与 superClass 的区别
在 Objective-C 中,[self class] 和 [super class] 都用于获取对象的类信息,但它们在运行时的行为略有不同。理解它们的区别有助于更好地掌握 Objective-C 的消息传递机制和继承关系。让我们详细解释这两个调用的区别。 [self class] 当你在一个对象方…...
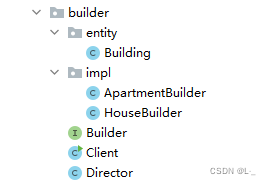
秒懂设计模式--学习笔记(6)【创建篇-建造者模式】
目录 5、建造者模式5.1 介绍5.2 建造步骤的重要性5.3 地产开发商的困惑5.4 建筑施工方5.5 工程总监5.6 项目实施5.7 建造者模式的各角色定义5.8 建造者模式 5、建造者模式 5.1 介绍 建造者模式(Builder)又称为生成器模式,主要用于对复杂对象…...
领略超越王勃的AI颂扬艺术:一睹其惊艳夸赞风采
今日,咱也用国产AI技术,文心一言3.5的文字生成与可灵的图像创作,自动生成一篇文章,提示语文章末下载。 【玄武剑颂星际墨侠】 苍穹为布,星辰织锦,世间万象,皆入我玄武剑公众号之浩瀚画卷。此号…...

Linux走进网络
走进网络之网络解析 目录 走进网络之网络解析 一、认识计算机 1.计算机的发展 2.传输介质 3.客户端与服务器端的概念 交换机 路由器 二、计算机通信与协议 1. 协议的标准化 2. 数据包的传输过程 OSI 协议 ARP协议 3. TCP/IP:四层模型 4. TCP三次握手和四次挥手…...

go语言Gin框架的学习路线(六)
gin的路由器 Gin 是一个用 Go (Golang) 编写的 Web 框架,以其高性能和快速路由能力而闻名。在 Gin 中,路由器是框架的核心组件之一,负责处理 HTTP 请求并将其映射到相应的处理函数上。 以下是 Gin 路由器的一些关键特性和工作原理的简要解释…...

Java面经知识点汇总版
Java面经知识点汇总版 算法 14. 最长公共前缀(写出来即可) Java 计算机基础 数据库 基础 SQL SELECT first_name, last_name, salary FROM employees WHERE department Sales AND salary > (SELECT AVG(salary)FROM employeesWHERE department Sal…...

详细分析Sql Server中的declare基本知识
目录 前言1. 基本知识2. Demo3. 拓展Mysql4. 彩蛋 前言 实战探讨主要来源于触发器的Demo 1. 基本知识 DECLARE 语句用于声明变量 声明的变量可以用于存储临时数据,并在 SQL 查询中多次引用 声明变量:使用 DECLARE 语句声明一个或多个变量变量命名&a…...

Perl 语言入门:编写并执行你的第一个脚本
摘要 Perl 是一种高级、通用的、解释型、动态编程语言,以其强大的文本处理能力而闻名。本文将指导初学者如何编写和执行他们的第一个 Perl 脚本,包括 Perl 的基本概念、脚本的基本结构、运行 Perl 脚本的方法以及一些简单的 Perl 语法。 引言 Perl&am…...

python库 - missingno
missingno 是一个用于可视化和分析数据集中缺失值的 Python 库。它提供了一系列简单而强大的工具,帮助用户直观地理解数据中的缺失模式,从而更好地进行数据清洗和预处理。missingno 库特别适用于数据分析和数据科学项目,尤其是在处理缺失数据…...

VPN的限制使得WinSCP无法直接连接到FTP服务器解决办法
由于VPN的限制使得WinSCP无法直接连接到FTP服务器,并且堡垒机的文件上传限制为500M,因此我们需要找到一种绕过这些限制的方法。以下是几个可行的方案: 方法1:通过分割文件上传 分割文件: 使用文件分割工具(…...

PCI DSS是什么?
PCI DSS,全称为Payment Card Industry Data Security Standard(支付卡行业数据安全标准),是由支付卡行业安全标准委员会(PCI Security Standards Council)制定的一套安全标准,旨在保护信用卡信息…...

DeepMind的JEST技术:AI训练速度提升13倍,能效增强10倍,引领绿色AI革命
谷歌旗下的人工智能研究实验室DeepMind发布了一项关于人工智能模型训练的新研究成果,声称其新提出的“联合示例选择”(Joint Example Selection,简称JEST)技术能够极大地提高训练速度和能源效率,相比其他方法ÿ…...

如何使用 pytorch 创建一个神经网络
我已发布在:如何使用 pytorch 创建一个神经网络 SapientialM.Github.io 构建神经网络 1 导入所需包 import os import torch from torch import nn from torch.utils.data import DataLoader from torchvision import datasets, transforms2 检查GPU是否可用 dev…...
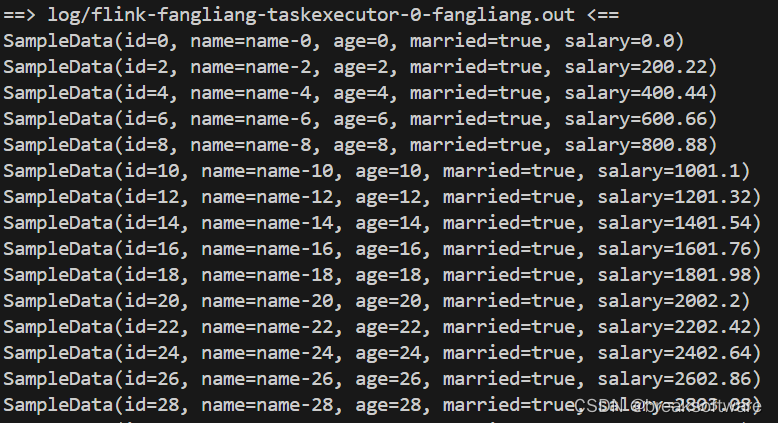
Java版Flink使用指南——定制RabbitMQ数据源的序列化器
大纲 新建工程新增依赖数据对象序列化器接入数据源 测试修改Slot个数打包、提交、运行 工程代码 在《Java版Flink使用指南——从RabbitMQ中队列中接入消息流》一文中,我们从RabbitMQ队列中读取了字符串型数据。如果我们希望读取的数据被自动化转换为一个对象&#x…...

CV每日论文--2024.7.8
1、DisCo-Diff: Enhancing Continuous Diffusion Models with Discrete Latents 中文标题:DisCo-Diff:利用离散潜伏增强连续扩散模型 简介:这篇文章提出了一种新型的离散-连续潜变量扩散模型(DisCo-Diff),旨在改善传统扩散模型(DMs)存在的问…...

【AI大模型】赋能儿童安全:楼层与室内定位实践与未来发展
文章目录 引言第一章:AI与室内定位技术1.1 AI技术概述1.2 室内定位技术概述1.3 楼层定位的挑战与解决方案 第二章:儿童定位与安全监控的需求2.1 儿童安全问题的现状2.2 智能穿戴设备的兴起 第三章:技术实现细节3.1 硬件设计与选择传感器选择与…...

云服务器linux系统安装配置docker
在我们拿到一个纯净的linux系统时,我需要进行一些基础环境的配置 (如果是云服务器可以用XShell远程连接,如果连接不上可能是服务器没开放22端口) 下面是配置环境的步骤 sudo -s进入root权限:退出使用exit sudo -i进入…...
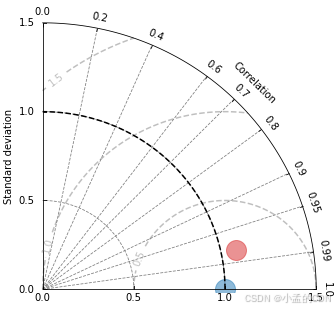
泰勒雷达图2
matplotlib绘制泰勒雷达图 import matplotlib.pyplot as plt import numpy as np from numpy.core.fromnumeric import shape import pandas as pd import dask.dataframe as dd from matplotlib.projections import PolarAxes import mpl_toolkits.axisartist.floating_axes a…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
