Studying-代码随想录训练营day31| 56.合并区间、738.单调递增的数字、968.监控二叉树、贪心算法总结
第31天,贪心最后一节(ง •_•)ง💪,编程语言:C++
目录
56.合并区间
738.单调递增的数字
968.监控二叉树
贪心算法总结
56.合并区间
文档讲解:代码随想录合并区间
视频讲解:手撕合并区间
题目:

学习:本题属于区间问题,同样是找到重合的区间,与用最少数量的箭引爆气球和无重叠区间问题解法是相同的。
本题可以先对区间进行排序,便于找到重叠区间,可以依照每个区间的左边界从小到大排序。之后比较后续区间的左边界,与前一个区间的右边界的关系,判断是否重叠。如果不重叠,则加入答案数组中,如果重叠则更新最大右边界。
代码:
//时间复杂度O(nlogn)快速排序时间复杂度
//空间复杂度O(logn)快速排序空间复杂度
class Solution {
public:static bool camp(vector<int>& a, vector<int>& b) {return a[0] < b[0];}vector<vector<int>> merge(vector<vector<int>>& intervals) {//先进行排序,按照开始节点进行排序sort(intervals.begin(), intervals.end());vector<vector<int>> result; //返回数组//初始化左右边界int left = intervals[0][0];int right = intervals[0][1];for(int i = 1; i < intervals.size(); i++) {if(intervals[i][0] <= right) {right = max(right, intervals[i][1]);}else {result.push_back({left, right});right = intervals[i][1];left = intervals[i][0];}}//把最后一个点加入result.push_back({left, right});return result;}
};本题还可以不设置单独的left,right来作为左边边界,而是使用back()来作为右边界进行更新。同时由于我们提前进行了排序,左边界又能够保证是按从小到大顺序进入的。
代码:
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {//使用lambda表达式sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){return a[0] < b[0];});vector<vector<int>> result; //返回数组//使用back()来确定result.push_back(intervals[0]); //初始化区间for(int i = 1; i < intervals.size(); i++) {if(intervals[i][0] <= result.back()[1]) {result.back()[1] = max(result.back()[1], intervals[i][1]);}else {result.push_back(intervals[i]);}}return result;}
};738.单调递增的数字
文档讲解:代码随想录单调递增的数字
视频讲解:手撕单调递增的数字
题目:

学习:本题重点在于需要比较每个位上的大小,来判断是否是单调递增的。贪心的方法就在于如果数不是单调递增的该如何处理。假设出现 num[i - 1] > num[i] 的情况,也就是前一位比后一位大的情况。由于需要单调递增,且不允许增大数,因此我们的贪心逻辑是,一旦出现num[i - 1] > num[i]的情况,我们就将前一位num[i - 1]--,同时将num[i]及以后的位变为9,这样就既能保证单调递增,数又是最大的。
本题我们需要从后往前遍历,我们需要利用后面比较的结果。以332为例子,如果从前往后遍历,将得到329,显然答案不对。如果从后往前遍历则是299,显然最终答案应该是这个。
写代码的时候可以注意两个关键点:
- 可以利用to_string()函数将数字变换为字符串,方便进行遍历处理。最后可以通过stoi()函数将字符串重新转变为int型变量。
- 可以设置一个flag位,确定后续要变9的位置,显然,我们只要找到最后一个需要减1的位置,后面的位就是需要置为9的。
代码:
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:int monotoneIncreasingDigits(int n) {//从后往前遍历,遇到前面的数大的情况,进行“前减一,后置9”的操作string str = to_string(n); //为了方便遍历,将int型变量转换为字符串(★)int flag = str.size(); //记录需要后置为9的位置//找到最后一个不单调的位置for(int i = str.size() - 1; i > 0; i--) {if(str[i] < str[i - 1]) {flag = i; //记录需要变9的位置str[i - 1]--; //进行减1} }for(int i = flag; i < str.size(); i++) {str[i] = '9'; //进行变9}return stoi(str);}
};968.监控二叉树
文档讲解:代码随想录监控二叉树
视频讲解:手撕监控二叉树
题目:

学习:本题的关键在于,思考如何放置摄像头才能使得摄像头的数量最小。从例子中我们可以发现,摄像头均没有放在叶子节点上。我们知道摄像头能够覆盖上中下三层,如果摄像头放在叶子节点上就必然会使得有一层是浪费的。虽然头节点放摄像头也会使得浪费一层,但是相较于头节点,叶子节点显然更多,因此叶子节点不放摄像头数量节省下来的是指数阶的。
本题的贪心就在于,局部最优:让叶子节点的父节点安装摄像头,摄像头数量最少;整体最优:全部摄像头数量所用最少。
理解了上述的贪心逻辑,我们还需要解决如下两个问题:1.二叉树的遍历;2.如何隔两个节点放一个摄像头。
1.二叉树的遍历顺序,显然我们要保证叶子节点的父节点有摄像头,且要尽可能的少放摄像头,我们需要从底往上,判断当前位置是否被覆盖,是否放置摄像头。因此需要采用后序遍历的方式。
2.如何隔两个节点放一个摄像头,对于一个节点来说,可能存在3种状态:没有被覆盖,该处有摄像头,该处没有摄像头但是被覆盖。而对于一个节点是否要安装一个摄像头,我们就需要判断左右孩子处于什么状态,如果左右孩子有一个处于没有被覆盖的状态,我们就需要在当前节点安装一个摄像头,并告诉其父节点自身有摄像头。
基于以上需求,我们可以设置3个数字来表示,当前节点的状态:
- 0:该节点无覆盖
- 1:本节点有摄像头
- 2:本节点有覆盖。
然后通过递推关系,来判断当前节点应该处于什么状态。如果处于1状态,我们就需要记录一个摄像头。
接下来我们就需要进行遍历过程中,递归三部曲的设置了:
1.确定返回值和参数列表:由于我们需要使用三个数字来表示当前节点的状态,因此我们返回值需设置为int型,参数列表传入root。
2.确定终止条件:由于我们需要左右孩子的情况,来判断当前节点处于的状态,因此我们需要遍历到最后的空节点(解决只有左右一个孩子的情况),而对于空节点应该处于什么状态,我们需要进行确定。为了让叶子节点不放摄像头,而叶子节点的父节点放摄像头,则叶子节点应该处于无覆盖的情况,且不能放置摄像头,因此空节点应该处于的是有覆盖的情况,这样才能推出叶子节点是无覆盖的。
3.单层递归逻辑:采用的是后序遍历,而后我们需要处理的“中”逻辑有四种情况:
- 左右节点都有覆盖:则此时中间节点就应该是无覆盖的情况
- 左右节点至少有一个无覆盖的情况:则中间节点应该安装一个摄像头。
- 左右节点至少有一个有摄像头:则中间节点处于有覆盖的情况。
- 头结点没有覆盖:头节点我们需要单独进行处理,因为头节点可能处于没有覆盖的情况。
基于以上,我们可以写出代码:
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:int result = 0; //定义全局变量,记录摄像头的个数//遍历树,1.确定返回值和参数列表//我们使用0,1,2来表示当前节点的三种状态:无覆盖(0)、有摄像头(1)、有覆盖(2);int traversal(TreeNode* root) {//确定终止条件if(root == nullptr) {return 2; //为了让叶子节点的父节点安装摄像头,空节点应设置为有覆盖,这样遍历到叶子节点默认左右孩子为有覆盖自身为无覆盖。}//采用后续遍历的方式,进行单层递归逻辑int left = traversal(root->left); //左int right = traversal(root->right); //右//中:分为三种情况//1.左右孩子均为有覆盖if(left == 2 && right == 2) {return 0; //则当前节点返回无覆盖}//2.左右孩子有一个是无覆盖(包含了5种情况)// left == 0 && right == 0 左右节点无覆盖// left == 1 && right == 0 左节点有摄像头,右节点无覆盖// left == 0 && right == 1 左节点有无覆盖,右节点摄像头// left == 0 && right == 2 左节点无覆盖,右节点覆盖// left == 2 && right == 0 左节点覆盖,右节点无覆盖if(left == 0 || right == 0) {result++; //则该节点需要有一个摄像头return 1;}//3.在上一个情况筛选的基础上,左右孩子有一个是有摄像头的if(left == 1 || right == 1) {return 2; //返回有覆盖}return -1; //在没有写else的情况下,需要加一个return,但实际上该return不会运行到}int minCameraCover(TreeNode* root) {//头节点单独处理判断if(traversal(root) == 0) { //如果头节点没有被覆盖result++;}return result;}
};贪心算法总结
文档讲解:代码随想录贪心算法总结
贪心算法一句话:没有套路,多加练习,手动模拟。
贪心算法的题目可以分为:

题目之间并没有明显的顺序关系,重点还是要多加联系。
一个系列的结束,标志着另一个系列的开始,动态规划!继续加油💪
相关文章:

Studying-代码随想录训练营day31| 56.合并区间、738.单调递增的数字、968.监控二叉树、贪心算法总结
第31天,贪心最后一节(ง •_•)ง💪,编程语言:C 目录 56.合并区间 738.单调递增的数字 968.监控二叉树 贪心算法总结 56.合并区间 文档讲解:代码随想录合并区间 视频讲解:手撕合并区间 题目…...

springboot装修接单平台-计算机毕业设计源码25005
摘要 随着装修行业的快速发展和数字化趋势,传统的装修接单方式已显不足以满足用户需求,因此建立一个便捷高效的平台具有重要意义。通过利用Java语言的跨平台特性和强大的编程能力,结合SpringBoot框架的快速开发特性和Mysql数据库的稳定性&…...

matlab仿真 信道(下)
(内容源自详解MATLAB/SIMULINK 通信系统建模与仿真 刘学勇编著第四章内容,有兴趣的读者请阅读原书) 之前的内容还剩下simulink的仿真过程。 3.simulink中的AWGN模块仿真 系统框图如图所示,TX和RX 模块需要单独实现…...
华宇携TAS应用中间件亮相2024年山东江信智能信创产品推介会
信创产业是数据、网络安全的基础,也是“新基建”的重要内容,将成为拉动经济发展的重要抓手之一。 7月5日,以“信守时代机遇,创造辉煌未来”为主题的山东江信智能信创产品推介会在济南举办。本次产品推介会汇聚了国内众多信息技术…...
)
单向链表的数据存储(申请堆空间)
函数功能: 0.排序(逆置和顺序排序) 1.回显 2.头插 3.位插 4.尾插 5.尾删 6.头删 7.位删 8.查找 (按值或按位查找) 9.修改 (按值或按位修改) 10.退出 main.c …...

MySQL8之mysql-community-common的作用
在MySQL 8中,mysql-community-common是一个软件包,它提供了MySQL服务器和客户端库所需的一些共同文件。具体来说,mysql-community-common的作用包括但不限于以下几点: 1. 提供基础配置和错误信息 错误信息和字符集包:…...

Emacs有什么优点,用Emacs写程序真的比IDE更方便吗?
Emacs 是一个功能强大的文本编辑器和应用程序框架,它拥有众多的优点,这些优点使得它在某些情况下成为编程的强大工具。然而,是否用 Emacs 写程序比 IDE 更方便,这很大程度上取决于个人的工作习惯和偏好。 Emacs 的主要优点包括&a…...

如何切换手机的ip地址
在数字时代的浪潮中,智能手机已成为我们日常生活中不可或缺的一部分。然而,随着网络安全问题的日益凸显,保护个人隐私和数据安全变得尤为重要。其中,IP地址作为网络身份的重要标识,其安全性与隐私性备受关注。本文将详…...

前端画图引擎ZRender,echarts的渲染器,你知道吗?
Zrender是一个轻量级的Canvas和SVG渲染库,它提供了一个高性能的图形绘制和交互的解决方案,用于在Web页面上创建丰富的数据可视化和交互式图形。 可能大部分小伙伴不知道这个类库,本文给大家科普一下。 一、Zrender是谁? 该项目…...

web前端开发——标签一
今天我来针对web前端开发讲解标签一 Html标签_标题&段落&换行 注释标签:Ctrl/ Ctrl/ ,用户可能会获取到注释标签 注释的原则: •和代码逻辑一致 •尽量使用中文 •正能量 标题标签:<h1></h1> h1-h6 标题标签有6…...

【深度学习】探讨最新的深度学习算法、模型创新以及在图像识别、自然语言处理等领域的应用进展
深度学习作为人工智能领域的重要分支,近年来在算法、模型以及应用领域都取得了显著的进展。以下将探讨最新的深度学习算法与模型创新,以及它们在图像识别、自然语言处理(NLP)等领域的应用进展。 一、深度学习算法与模型创新 新型…...
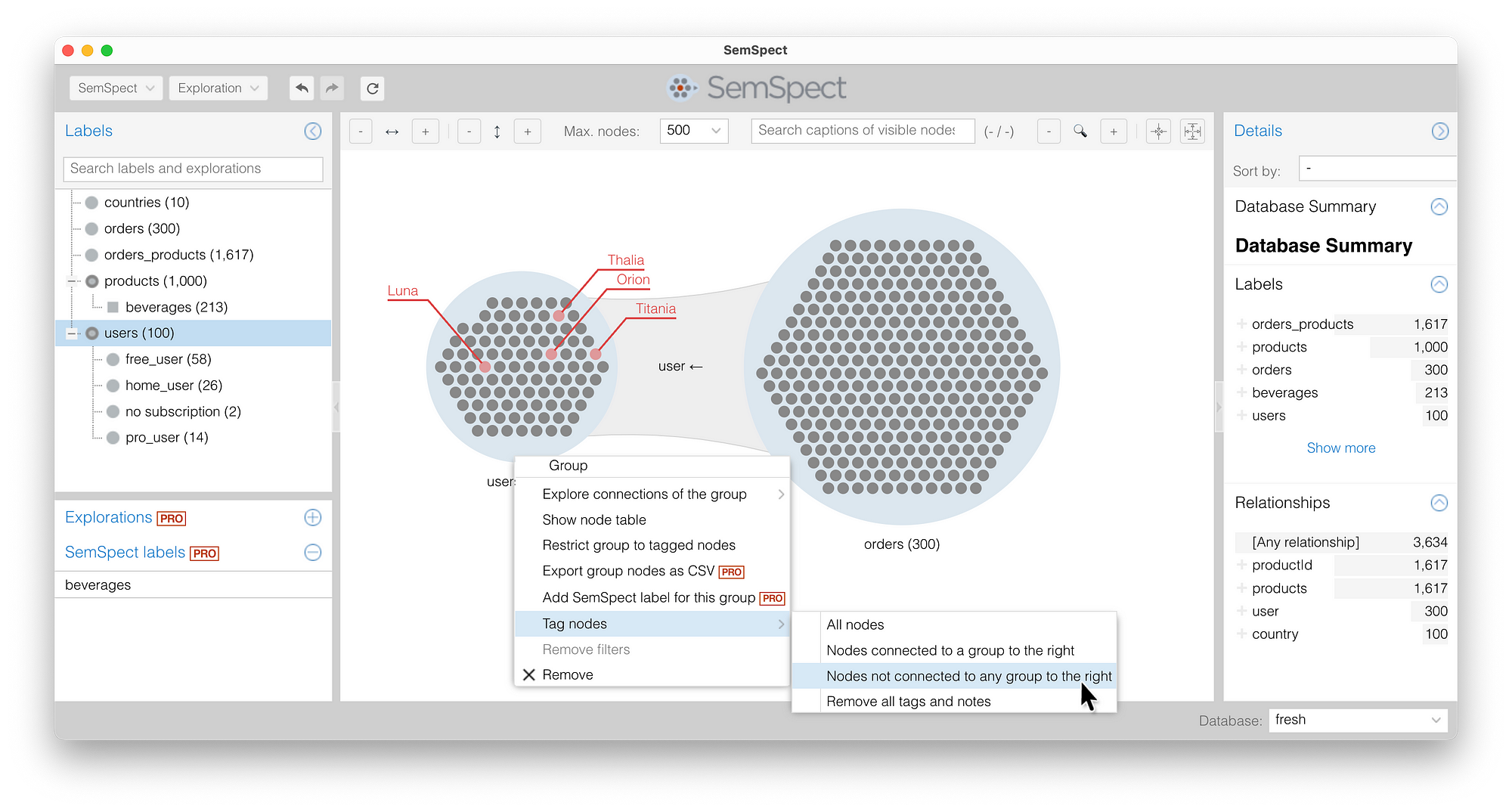
使用 mongo2neo4j 和 SemSpect 通过各种方式进行图探索
用于可视化和探索每个 MEAN 堆栈背后的数据图的 ETL 您是否正在努力回答有关 MEANS Web 服务数据的紧急问题?哪里有 BI 可以快速回答“上个季度哪些亚洲的artisan.plus 用户触发了订单?”这个问题,而无需编写查询?使用 mongo2neo4…...

淘宝卖家难免遇到的商品问题 在淘宝买的东西出问题了,该如何维权
很多朋友对于淘宝卖家难免遇到的商品问题和在淘宝买的东西出问题了,该如何维权不太懂,今天就由小编来为大家分享,希望可以帮助到大家,下面一起来看看吧! [1] 淘宝买东西,过了售后期,有质量问题怎…...
encoder)
ffmpeg 安装 h264(x264)encoder
#下载并安装x264 # 切换root用户 sudo -i # 输入密码cd ~ mkdir FFmpeg7#下载并安装x264 git clone https://code.videolan.org/videolan/x264.git cd x264 mkdir build./configure --help # 报缺少asm 时 可加入--disable-asm # --prefix/home/llh/ffmpeg/build/ 指定安装目录…...

Java项目:基于SSM框架实现的健康综合咨询问诊平台【ssm+B/S架构+源码+数据库+毕业论文】
一、项目简介 本项目是一套基于SSM框架实现的健康综合咨询问诊平台 包含:项目源码、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过严格调试,eclipse或者idea 确保可以运行! 该系统功能完善、界面美观、操作简单、…...

SpringBoot源码阅读(4)——事件
从监听器到事件 SpringApplication运行中触发事件,多播器发送事件到监听器,监听器处理事件。 SpingApplication中事件都是经过SpringApplicationRunListeners类传送到各个监听器。 以starting事件为例 void starting(ConfigurableBootstrapContext boo…...
EDI安全:如何在2024年保护您的数据免受安全和隐私威胁
电子数据交换(EDI)支持使用标准化格式在组织之间自动交换业务文档。这种数字化转型彻底改变了业务通信,消除了对纸质交易的需求并加速了交易。然而,随着越来越依赖 EDI 来传输发票、采购订单和发货通知等敏感数据,EDI …...

RabbitMQ快速入门 - 图像化界面的简单操作
目录 1、RabbitMQ的安装 2、RabbitMQ基本介绍 3、简单案例 4、数据隔离 1、RabbitMQ的安装 官网链接:rabbitmq官网 (官网很详细,也可以在官网学习啦~) 基础入门:自主学习:最新版本:安装我…...

新版亚组交互效应函数(P for interaction)newscitb5 1.3版本发布--用于一键生成交互效应表
在SCI文章中,交互效应表格(通常是表五)能为文章锦上添花,增加文章的信服力,增加结果的可信程度,还能进行数据挖掘。什么是亚组,通常就是特殊类型人群,比如男女,种族等&am…...

gpt讲 Observable 对象
什么是 Observable? Observable 是一种用于处理异步数据流的数据类型。它可以发出多个值,这些值可以是同步或者异步产生的,并且可以在时间上发生变化。在 Angular 中,HttpClient 返回的响应对象、事件流以及许多其他异步任务都可…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
