【深度学习】第3章——回归模型与求解分析
一、回归分析
1.定义
分析自变量与因变量之间定量的因果关系,根据已有的数据拟合出变量之间的关系。
2.回归和分类的区别和联系

3.线性模型

4.非线性模型

5.线性回归※
面对回归问题,通常分三步解决
第一步:选定使用的model,即确定函数模型是一次函数 还是二次函数,甚至是更高的三次四次或者五次函数。
第二步:确定模型的损失函数loss function。
均方误差损失函数(MSE)的公式如下:
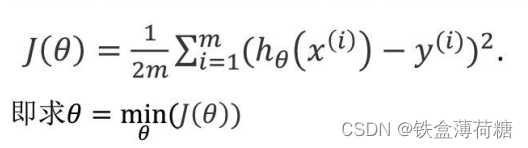
第三步:采用梯度下降,优化损失函数 (可以使用梯度下降的前提是损失函数可微分)。
二、多元回归与多项式回归
1.Sklearn的一元线性回归
在scikit-learn中,所有的估计器都带有fit( )方法和predict( )方法
fit()用来拟合模型,predict()利用拟合出来的模型对样本进行预测。
例如:
from sklearn.linear_model import LinearRegression# 创建并拟合模型
model = LinearRegression()
X = [[6], [8], [10], [14], [18]]
y = [[7], [9], [13], [17.5], [18]]
model.fit(X, y)# 预测12英寸披萨的价格
predict方法的输入应当是一个2D数组,而不是一个单独的整数。
#例如:predicted = model.predict([[12], [16]])
#predicted_price_12 = predicted[0][0] # 15.0
#predicted_price_16 = predicted[1][0] # 20.0predicted_price = model.predict([[12]])[0][0]
print('预测12英寸披萨价格: $%.2f' % predicted_price)2.多元线性回归
from sklearn.linear_model import LinearRegressionX = [[6, 2], [8, 1], [10, 0], [14, 2], [18, 0]]
# 特征数据集,包含两个特征:披萨尺寸和其他因素(例如配料数量)
y = [[7], [9], [13], [17.5], [18]]
# 目标数据集,披萨价格model = LinearRegression()
# 创建线性回归模型实例
model.fit(X, y)
# 使用特征数据X和目标数据y训练模型X_test = [[8, 2], [9, 0], [11, 2], [16, 2], [12, 0]]
# 测试数据集,包含待预测的披萨尺寸和其他因素
y_test = [[11], [8.5], [15], [18], [11]]
# 测试目标数据集,对应测试数据集的实际披萨价格predictions = model.predict(X_test)
# 使用训练好的模型预测测试数据集的披萨价格for i, prediction in enumerate(predictions):# 遍历预测结果print('Predicted: %s, Target: %s' % (prediction, y_test[i]))# 输出预测价格和实际目标价格print('R-squared: %.2f' % model.score(X_test, y_test))
# 计算并输出模型在测试数据集上的R-squared值,表示模型的拟合优度
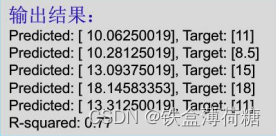
其中,model.score(X_test, y_test)是在计算模型在 X_test 数据集上预测的 y_test 值与实际 y_test 值之间的拟合优度,即R-squared 值(决定系数),它表示目标变量的方差有多少可以通过特征变量来解释。

3.多项式回归

三、损失函数的正则化



from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score# 加载数据集
data = load_iris()
X, y = data.data, data.target# 定义模型
model = LogisticRegression(max_iter=200)# 定义正则化参数的网格
param_grid = {'C': [0.01, 0.1, 1, 10, 100]
}# 使用 GridSearchCV 进行超参数搜索
grid_search = GridSearchCV(model, param_grid, cv=5, scoring='accuracy')
grid_search.fit(X, y)# 输出最佳参数和最佳分数
print("Best parameters found: ", grid_search.best_params_)
print("Best cross-validation score: ", grid_search.best_score_)# 使用最佳参数训练模型
best_model = grid_search.best_estimator_
best_model.fit(X, y)# 预测并计算准确率
y_pred = best_model.predict(X)
print("Training accuracy: ", accuracy_score(y, y_pred))
四、逻辑回归
逻辑回归可以被理解为是一个被logistic函数归一化后的线性回归,也可以被视为一种广义线性模型。
1.逻辑回归中的损失函数优化方法

相关文章:

【深度学习】第3章——回归模型与求解分析
一、回归分析 1.定义 分析自变量与因变量之间定量的因果关系,根据已有的数据拟合出变量之间的关系。 2.回归和分类的区别和联系 3.线性模型 4.非线性模型 5.线性回归※ 面对回归问题,通常分三步解决 第一步:选定使用的model,…...

Maven的基本使用
引入依赖 1.引入Maven仓库存在的依赖,直接引入,刷新Maven <dependency><groupId>org.springframework</groupId><artifactId>spring-webmvc</artifactId><version>5.2.12.RELEASE</version> </dependency…...

【笔记】finalshell中使用nano编辑器GNU
ctrl O 保存 enter 确定 ctrl X 退出 nano编辑 能不用就不用吧 因为我真用不习惯 nano编辑的文件也可以用vim编辑的...

markdown文件转pdf
步骤:md转html转pdf pom引入 <!--markdown 转pdf--><dependency><groupId>com.vladsch.flexmark</groupId><artifactId>flexmark-all</artifactId><version>0.64.8</version></dependency><dependency&g…...
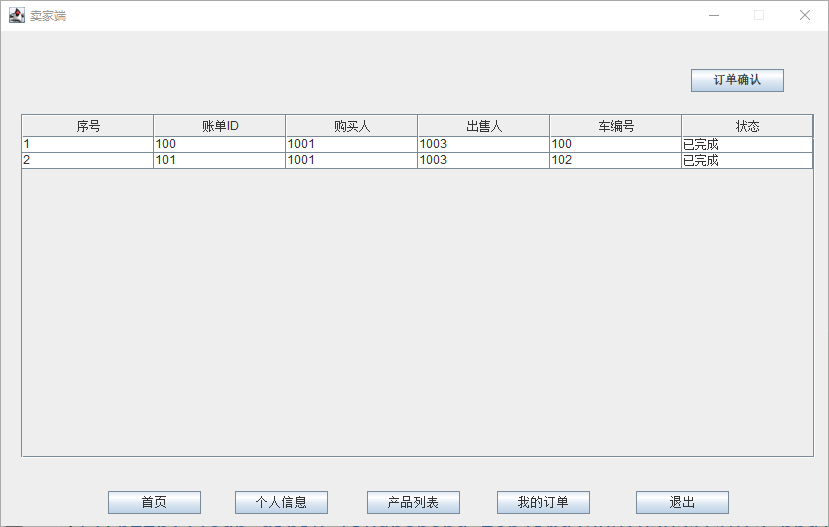
课设:二手车交易管理系统(Java+MySQL)
简易数据库课程设计~分享 技术栈 本项目使用以下技术栈构建: Java: 作为主要编程语言,负责业务逻辑的实现。MySQL: 用于数据存储,管理用户、车辆和订单信息。JDBC: 用于Java与MySQL数据库之间的连接和操作。Swing GUI: 提供用户图形界面&am…...

vue3实现无缝滚动 列表滚动 vue3-seamlessscroll
vue3框架内使用无缝滚动,使用一个插件比较合适(gitee地址): vue3-seamless-scroll: Vue3.0 无缝滚动组件 具体更多配置请看: 组件配置 | vue3-scroll-seamless 1. 安装: npm install vue3-seamless-sc…...

Python酷库之旅-第三方库Pandas(012)
目录 一、用法精讲 28、pandas.HDFStore.keys函数 28-1、语法 28-2、参数 28-3、功能 28-4、返回值 28-5、说明 28-6、用法 28-6-1、数据准备 28-6-2、代码示例 28-6-3、结果输出 29、pandas.HDFStore.groups函数 29-1、语法 29-2、参数 29-3、功能 29-4、返回…...

SpringCloud集成nacos之jasypt配置中心的密码加密的自动解密
目录 1.引入相关的依赖 2.nacos的yaml的相关配置,配置密码和相关算法 3.配置数据源连接 3.1 数据库连接配置 4.连接数据库配置类详解(DataSourceConfig)。 5.完整的配置类代码如下 1.引入相关的依赖 <dependency><groupId>…...

Python 中将字典内容保存到 Excel 文件使用详解
概要 在数据处理和分析的过程中,经常需要将字典等数据结构保存到Excel文件中,以便于数据的存储、共享和进一步分析。Python提供了丰富的库来实现这一功能,其中最常用的是pandas和openpyxl。本文将详细介绍如何使用这些库将字典内容保存到Excel文件中,并包含具体的示例代码…...

libaom 编码器 aomenc 使用文档介绍
使用方法:./aomenc <选项> -o 目标文件名 源文件名 使用 --help 查看完整的选项列表。 选项: --help 显示使用选项并退出-c <参数>, --cfg<参数> 使用配置文件-D, --debug 调试模式(使输出确定性)-o <参数&g…...

速盾:cdn 缓存图片
现如今,互联网已经成为我们日常生活中不可或缺的一部分。在我们使用互联网时,经常会遇到图片加载缓慢、文章打开慢等问题。为了解决这些问题,CDN(内容分发网络)应运而生。CDN 是一种通过将数据缓存在世界各地的服务器上…...
移动应用开发课设——原神小助手文档(2)
2023年末,做的移动应用开发课设,分还算高,项目地址:有帮助的话,点个赞和星呗~ GitHub - blhqwjs/-GenShin_imp: 2023年移动应用开发课设 本文按照毕业论文要求来写,希望对大家有所帮助。 接上文:…...

智能聊天机器人:使用PyTorch构建多轮对话系统
使用PyTorch构建多轮对话系统的示例代码。这个示例项目包括一个简单的Seq2Seq模型用于对话生成,并使用GRU作为RNN的变体。以下是代码的主要部分,包括数据预处理、模型定义和训练循环。 数据预处理 首先,准备数据并进行预处理。这部分代码假…...

昇思25天学习打卡营第16天 | 文本解码原理-以MindNLP为例
基于 MindSpore 实现 BERT 对话情绪识别 上几章我们学习过了基于MindSpore来实现计算机视觉的一些应用,那么从这期开始要开始一个新的领域——LLM 首先了解一下什么是LLM LLM 是 “大型语言模型”(Large Language Model)的缩写。LLM 是一种…...

Unity之Text组件换行\n没有实现+动态中英互换
前因:文本中的换行 \n没有换行而是打印出来了,解决方式 因为unity会默认把\n替换成\\n 面板中使用富文本这个选项啊 没有用 m_text.text m_text.text.Replace("\\n", "\n"); ###动态中英文互译 using System.Collections; using…...

vue3+ el-tree 展开和折叠,默认展开第一项
默认第一项展开: 展开所有项: 折叠所有项: <template><el-treestyle"max-width: 600px":data"treeData"node-key"id":default-expanded-keys"defaultExpandedKey":props"defaultProps"…...

ProFormList --复杂数据联动ProFormDependency
需求: (1)数据联动:测试数据1、2互相依赖,测试数据1<测试数据2,测试数据2>测试数据1。 (2)点击添加按钮,添加一行。 (3)自定义操作按钮。 ࿰…...

Git、Github、tortoiseGit下载安装调试全套教程
一、Git 1.下载安装Git 编辑器可默认Vim,可换成别的,此处换成VScode,换成VScode或别的都需要单独下载和调用 (1)Git安装:https://www.cnblogs.com/xiuxingzhe/p/9300905.html 超级完整的 Git的下载、安…...

老师怎么快速发布成绩?
期末考试的钟声刚刚敲响,成绩单的发放却成了老师们的一大难题。每当期末成绩揭晓,老师们便要开始一项繁琐的任务——将每一份成绩单逐一私信给家长。这不仅耗费了大量的时间和精力,也让本就忙碌的期末工作变得更加繁重。然而,随着…...

央视揭露:上百元的AI填报高考志愿真的靠谱吗?阿里云新增两位AI圈“代言人”!|AI日报
文章推荐 MiniMax闫俊杰:国内模型远不及GPT-4;OpenAI隐瞒黑客曾入侵其内部系统|AI日报 今日热点 月之暗面、智联招聘成为阿里云新“代言人”,使用阿里云强大算力和大模型服务平台提升模型推理效率 7月8日,阿里云官…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...

手动给中文分词和 直接用神经网络RNN做有什么区别
手动分词和基于神经网络(如 RNN)的自动分词在原理、实现方式和效果上有显著差异,以下是核心对比: 1. 实现原理对比 对比维度手动分词(规则 / 词典驱动)神经网络 RNN 分词(数据驱动)…...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...
