《RWKV》论文笔记
原文出处
[2305.13048] RWKV: Reinventing RNNs for the Transformer Era (arxiv.org)
原文笔记
What
RWKV(RawKuv):Reinventing RNNs for the Transformer Era
本文贡献如下:
提出了 RWKV 网络架构,结合了RNNS 和Transformer 的优点,同时缓解了它们已知的限制
我们提出了一种新的线性注意力机制
展示了 RWKV 在处理涉及大规模模型和长距离依赖关系的任务时的性能、效率和扩展能力
RWKV的突出卖点:
O(1)推理复杂度真的非常香
- 单 token 推理时间恒定,总推理时间随序列长度线性增加
- 内存占用恒定,不随序列长度增加
- 推理时间和内存占用随模型尺寸线性增长
优势是数量级级别的,这意味着:
- 大模型的硬件限制和部署成本将大幅降低,CPU及非 NV 加速卡均可部署
- 服务器上部署大模型的成本将大幅降低,普通台式机和笔记本将能在本地部署大模型手机端部署也成为可能
RWKV 将推动大模型进行一次架构迁移!
Why
Transformer具有出色的序列建模能力,一次处理一整句话,或一整段话,可以并行训练,但是同样面临着计算复杂度高,内存占用大,计算成本高的难题
传统的Transformer的总推理时间随序列长度二次增加(在序列特别长的情况下有可能三次增加)
自注意力机制的二次复杂度使其成为涉及长序列和受限资源的任务的计算和内存密集型。这刺激了增强 Transformer 可扩展性的研究,有时牺牲了一些其有效性
循环神经网络 (RNN) 在内存和计算需求方面表现出线性缩放,内存占用小,计算量小,(因为他每次只处理一部的数据)但由于并行化和可扩展性的限制,难以与 Transformer 匹配相同的性能。
RNN在训练长序列时容易出现梯度消失问题
RNN 在训练过程中对前一步结果依赖,无法在时间维度上进行并行化,限制了其可扩展性(无法获得很大的rnn模型)
RWKV 背后的动机是平衡计算效率和神经网络的表达能力。它提供了一种处理具有数十亿个参数的大规模模型的解决方案,以降低计算成本表现出具有竞争力的性能。实验表明,RWKV 解决了 AI 中的缩放和部署挑战,特别是对于顺序数据处理,指向更可持续和高效 AI 模型。
Challenge
Idea
model
容我再整理整理
原文翻译
Abstract
Transformers 彻底改变了几乎所有自然语言处理 (NLP) 任务,但受到内存和计算复杂性的影响,这些复杂性随序列长度呈二次方扩展。相比之下,循环神经网络 (RNN) 在内存和计算需求方面表现出线性缩放,但由于并行化和可扩展性的限制,难以与 Transformer 匹配相同的性能。我们提出了一种新颖的模型架构,即感知加权键值 (RWKV),它将变压器的高效并行训练与 RNN 的有效推理相结合。
我们的方法利用了线性注意力机制,并允许我们将模型制定为 Transformer 或 RNN,从而在训练期间并行化计算并在推理过程中保持恒定的计算和内存复杂性。到目前为止,我们将我们的模型扩展到多达 14 亿个参数,是迄今为止训练的最大密集 RNN,发现 RWKV 的性能与类似大小的 Transformer 相当,这表明未来的工作可以利用这种架构来创建更有效的模型。这项工作为协调序列处理任务中计算效率和模型性能之间的权衡迈出了重要的一步。
Introduction
深度学习极大地推动了人工智能,影响了一系列科学和工业用途。这些通常涉及复杂的顺序数据处理任务比如自然语言理解任务,会话AI,时间序列分析,和间接顺序格式,如图像和图表(Brown等人,2020;Ismail Fawaz等人,2019;Wu等人,2020;Albalak等人,2022)。这些技术中占主导地位包括 RNN 和 Transformers (Vaswani et al., 2017),每种都有特定的优点和缺点。RNN 需要更少的内存,特别是对于处理长序列。然而,它们在训练过程中在时间维度上存在梯度消失问题和非并行性,限制了它们的可扩展性(Hochreiter,1998;Le 和 Zuidema,2016)。
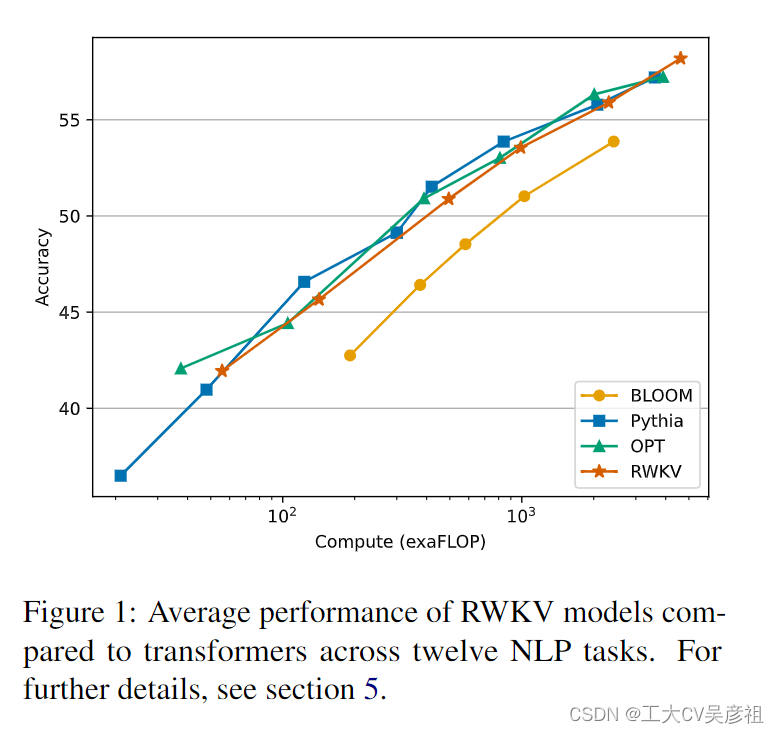
Transformers 已经成为一种强大的替代方案,擅长管理局部和远程依赖项并支持并行训练(Tay 等人,2022 年)。诸如GPT-3 (Brown et al., 2020)、ChatGPT (OpenAI, 2022;Kocón et al., 2023),LLAMA (Touvron et al., 2023) 和 Chinchilla (Hoffmann et al., 2022) 展示了 Transformer 在 NLP 中的潜力。然而,自注意力机制的二次复杂度使其成为涉及长序列和受限资源的任务的计算和内存密集型。这刺激了增强 Transformer 可扩展性的研究,有时牺牲了一些其有效性(Wang 等人,2020;Zaheer 等人,2020;Dao 等人,2022a)。
为了应对这些挑战,我们引入了感知加权键值 (RWKV) 模型,结合了 RNN 和 Transformer 的优势,同时规避了关键缺陷。RWKV 通过高效的线性缩放缓解了与 Transformer (Katharopoulos et al., 2020) 相关的内存瓶颈和二次缩放,同时保持 Transformer 的表达能力,例如并行训练和鲁棒可扩展性。RWKV 用线性注意力的变体重新制定注意力机制,用更有效的通道定向注意力替换传统的点积令牌交互。这种实现,没有近似,提供了最低的计算和内存复杂性;见表 1。
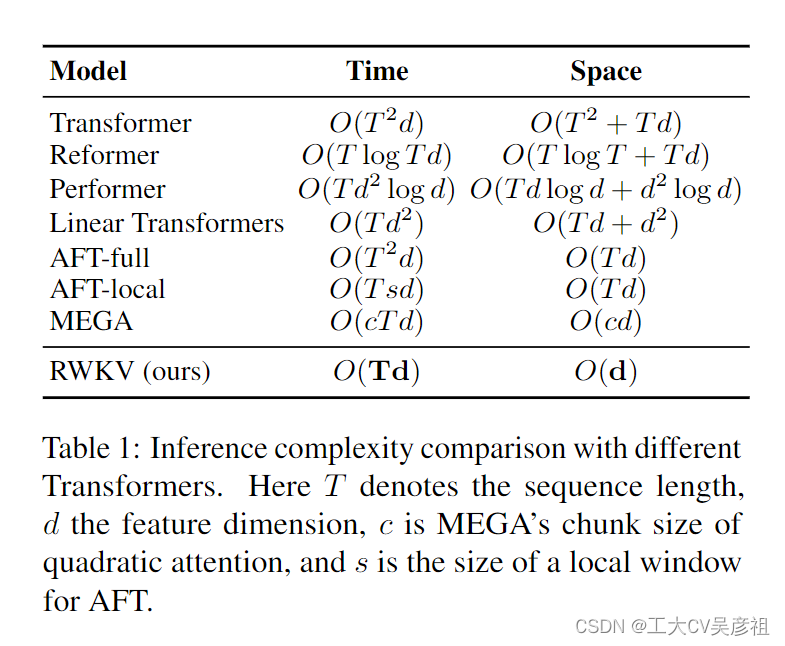
RWKV 背后的动机是平衡计算效率和神经网络的表达能力。它提供了一种处理具有数十亿个参数的大规模模型的解决方案,以降低计算成本表现出具有竞争力的性能。实验表明,RWKV 解决了 AI 中的缩放和部署挑战,特别是对于顺序数据处理,指向更可持续和高效 AI 模型。我们在本文中的贡献如下:
- RWKV 的引入,一种新颖的架构,结合了 RNN 和 Transformer 优势,同时减轻了它们的局限性。
- 详细的实验,展示了 RWKV 在大规模模型的基准数据集上的性能和效率。
- 预训练模型的释放,从 1690 万个参数到 14 亿个参数,在 Pile 上训练(Gao 等人,2020;Biderman 等人,2022)。
2 Background
在这里,我们简要回顾了 RNN 和 Transformer 的基本原理。
2.1 Recurrent Neural Networks (RNNs)
LSTM (Hochreiter and Schmidhuber, 1997) 和 GRU (Chung et al., 2014) 等流行的 RNN 架构的原理可以概括为以下公式(如 LSTM 所示,其他架构可以类似地推理):
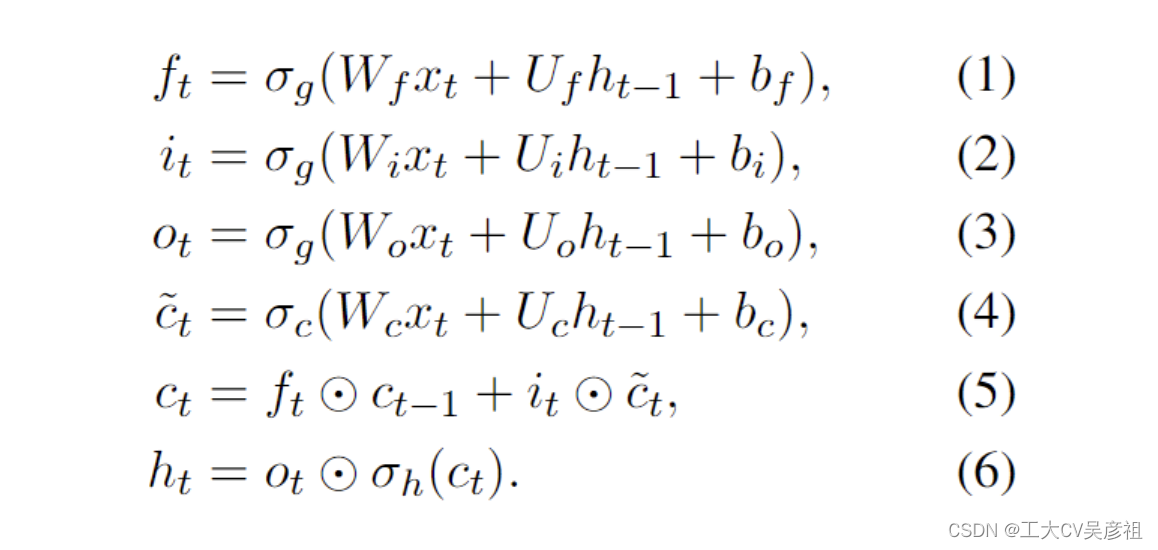
尽管RNN可以分解为两个线性块(W和U)和一个特定于RNN的块(1)-(6),如Bradbury等人所述。(2017),依赖于先前时间步长的数据依赖禁止并行化这些典型的RNN。
2.2 Transformers and AFT
由Vaswani等人(2017)介绍,Transformers是一类神经网络,已经成为几个NLP任务的主要架构。Transformer 不是像 RNN 那样逐步操作序列,而是依靠注意力机制来捕获所有输入和输出tokens之间的关系:
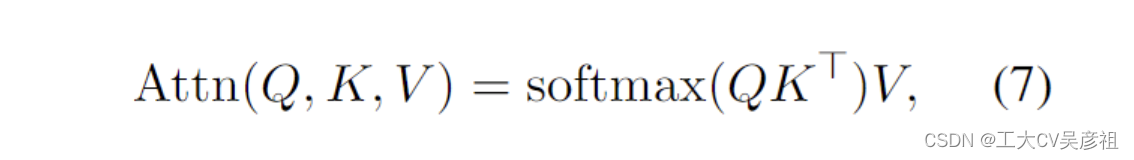
其中为方便起见,省略了多头和比例因子 1√dkis。核心 QK⊤ 乘法是一个在序列中的每个令牌之间成对注意力分数的集合,可以分解为向量操作:
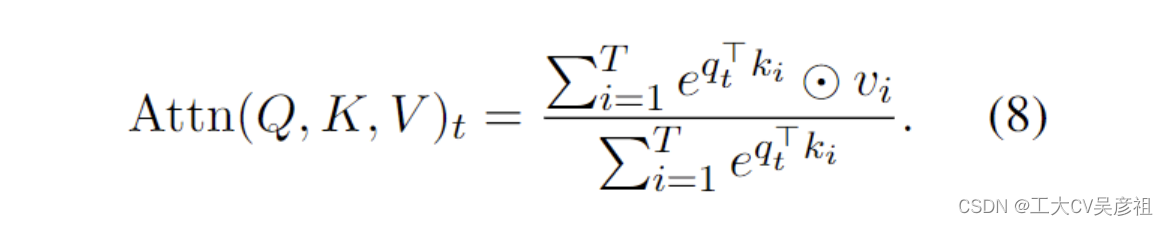
AFT (Zhai et al., 2021),表述为
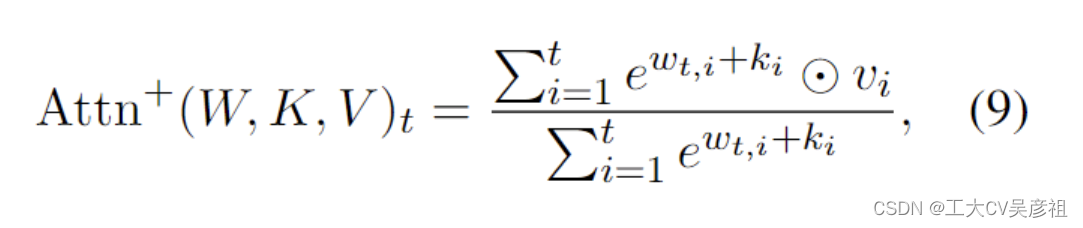
其中 {wt,i} ∈ RT ×T 是学习的成对位置偏差,每个 wt,i 是一个标量。
受 AFT 的启发,RWKV 采用类似的方法。但是,为简单起见,它修改了交互权重,使其可以转化为 RNN。RWKV 中的每个 wt,i 是一个通道时间衰减向量乘以相对位置并从当前时间向后跟踪,因为它衰减:
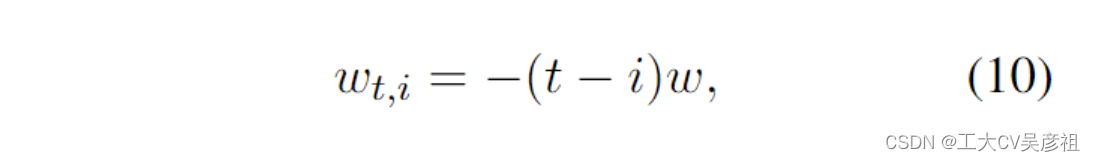
其中 w ∈ (R≥0)^d,d 是通道数。我们要求 w 是非负的,以确保 e^wt,i ≤ 1 并且每通道权重在时间上向后衰减。
距离当前token越远的token它就会衰减的越多,越近的token它就会衰减的越少,但实际情况比这个还要复杂一点,后边有个图来可视化这一部分(channel的信息衰减))
3 RWKV
RWKV模型架构由四个基本元素构成,这四个基本元素本质上都是时间混合的和通道混合的:
R:Receptance向量充当过去信息的接收器(作为过去信息的接受程度的接受向量)
W:Weight表示位置权重衰减向量,即模型中的可训练参数(可训练的模型参数)
K:键向量,类似于传统注意力机制中的K。(用每一个token自身的一个值来对位置向量进行调制)
V:值向量,类似于传统注意力机制中的V。
这些核心元素在每个时间步乘法交互,如图 2 所示。

3.1 Architecture
RWKV 模型由堆叠的残差块组成。每个块由一个时间混合和一个通道混合子块组成,实现循环结构以利用过去的信息。
该模型使用了独特的类似注意力的分数更新过程,其中包括一个随时间变化的 softmax 操作,以提高数值稳定性和减轻消失梯度(对于严格的证明,请参见附录 H)。它确保梯度沿着最相关的路径传播。此外,架构中包含的层归一化 (Ba et al., 2016) 有助于稳定梯度,有效地解决梯度消失和爆炸的问题。这些设计元素不仅增强了深度神经网络的训练动态,而且促进了多层的堆叠,通过捕获不同抽象级别的复杂模式,从而比传统的 RNN 模型具有更好的性能(另见附录 I)。
3.1.1 Token Shift
在该架构中,计算中涉及的所有线性投影向量(R, K, V,通道混合中的R ', K ')都是通过当前时间步输入和前一个时间步输入之间的线性插值产生的,促进令牌移位。
时间混合计算的向量是块当前输入和先前输入的线性组合的线性投影:

通道混合输入也是如此:

使用 PyTorch (Paszke et al., 2019) 库 asnn 在每个块的时间维度上实现令牌移位作为一个简单的偏移量。ZeroPad2d((0,0,1,-1))。
(在模型参数较小的时候与Transofrmer的效果还是有一定差距的)
3.1.2 WKV Operator
我们模型中的 W KV 算子的计算与 Attention Free Transformer (AFT) 中使用的方法并行(Zhai 等人,2021 年)。然而,与 W 是一个成对矩阵的 AFT 不同,我们的模型将 W 视为由相对位置修改的通道向量。在我们的模型中,这种循环行为由 W KV 向量的时间相关更新定义,形式化如下等式:

为了规避 W 的任何潜在退化,我们引入了一个单独关注当前标记的向量 U。有关这方面的更多信息可以在附录 I 中找到。
3.1.3 Output Gating
使用 sigmoid 在时间混合和通道混合块中实现输出门控,接受度,σ(r)。W KV 算子后输出向量 ot 由下式给出:

3.2 Transformer-like Training
RWKV 可以使用一种称为时间并行模式的技术有效地并行化,让人想起 Transformer。在单个层中处理一批序列的时间复杂度为 O(BT d2),主要由矩阵乘法 Wλ 组成,其中 λ ∈ {r, k, v, o}(假设 B 序列、Tmaximum 标记和 d 个通道)。相比之下,更新注意力分数wkvt涉及串行扫描(更多细节见附录D),复杂度为O(BT d)。矩阵乘法可以类似于 Wλ 并行化,其中传统 Transformer 中的 λ ∈ {Q, K, V, O}。逐元素 W KV 计算依赖于时间,但可以很容易地沿其他两个维度并行化 (Lei et al., 2018)3。
3.3 RNN-like Inference
循环网络通常利用状态 t 的输出作为状态 t + 1 的输入。在语言模型的自回归解码推理中也可以观察到这种用法,其中每个令牌必须在传递到下一步之前计算。RWKV 利用了这种类似 RNN 的结构,称为时间顺序模式。在这种情况下,RWKV 可以方便地在推理过程中递归制定用于解码,如附录 D 所示。
下略
相关文章:

《RWKV》论文笔记
原文出处 [2305.13048] RWKV: Reinventing RNNs for the Transformer Era (arxiv.org) 原文笔记 What RWKV(RawKuv):Reinventing RNNs for the Transformer Era 本文贡献如下: 提出了 RWKV 网络架构,结合了RNNS 和Transformer 的优点,同…...
——显色指数(Ra))
相机光学(二十九)——显色指数(Ra)
显指Ra是衡量光源显色性的数值,表示光源对物体颜色的还原能力。显色性是指光源对物体颜色的呈现能力,即光源照射在同一颜色的物体上时,所呈现的颜色特性。通常用显色指数(CRI)来表示光源的显色性,而显指Ra是…...

【Swoole 的生命周期,文件描述符,协程数量,以及默认值】
目录 Swoole 的生命周期 Swoole 文件描述符(FD)缓存 Swoole设置协程的数量 Swoole 默认值 Swoole 是一个基于 PHP 的高性能网络通信引擎,它采用 C 编写,提供了协程和高性能的网络编程支持。Swoole 支持多种网络服务器和客户端…...

“不要卷模型,要卷应用”之高考志愿填报智能体
摘要:李总的发言深刻洞察了当前人工智能领域的发展趋势与核心价值所在,具有高度的前瞻性和实践性。“大家不要卷模型,要卷应用”这一观点强调了在当前人工智能领域,应该更加注重技术的实际应用而非单纯的技术竞赛或模型优化。个性…...

k8s离线部署芋道源码后端
目录 概述实践Dockerfilek8s部署脚本 概述 本篇将对 k8s离线部署芋道源码后端 进行详细的说明,对如何构建 Dockerfile,如何整合 Nginx,如何整合 ingress 进行实践。 相关文章:[nacos在k8s上的集群安装实践] k8s离线部署芋道源码前…...
图论·Day01
P3371 P4779 P3371 【模板】单源最短路径(弱化版) 注意的点: 边有重复,选择最小边!对于SPFA算法容易出现重大BUG,没有负权值的边时不要使用!!! 70分代码 朴素板dijsk…...

hutool ExcelUtil 导出导入excel
引入依赖 <dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>5.8.15</version></dependency>文件导入 public void savelist(String filepath,String keyname){ExcelReader reader Exce…...

打卡第7天-----哈希表
继续坚持✊,我现在看到leetcode上的题不再没有思路了,真的是思路决定出路,在做题之前一定要把思路梳理清楚。 一、四数相加 leetcode题目编号:第454题.四数相加II 题目描述: 给定四个包含整数的数组列表 A , B , C , …...
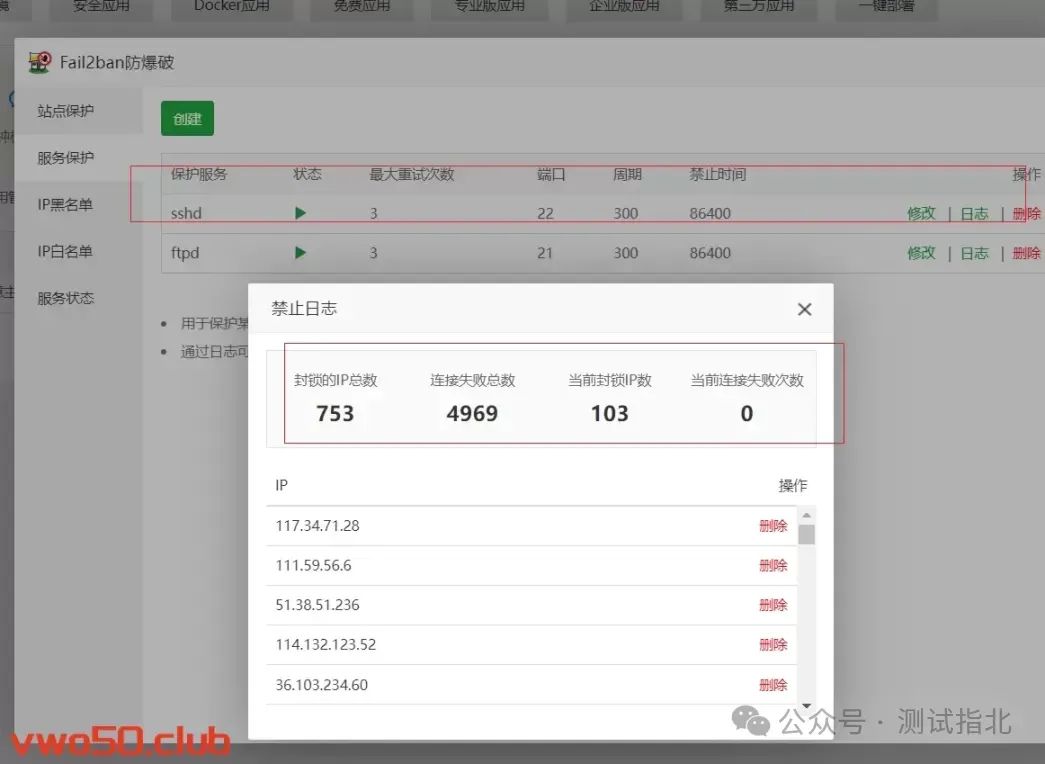
【Linux】WEB网站网络防火墙(WAF软件)Fail2ban:保护服务器免受恶意攻击的必备工具
随着互联网的迅速发展,服务器的安全性日益成为用户和管理员关注的焦点。恶意攻击者不断寻找机会侵入服务器,窃取敏感信息、破坏数据或者滥用系统资源。为了抵御这些威胁,许多安全工具应运而生,其中一款备受推崇的工具就是 Fail2ba…...

妙笔生词智能写歌词软件:创新助力还是艺术之殇?
在音乐创作日益普及和多样化的当下,各种辅助工具层出不穷,妙笔生词智能写歌词软件便是其中之一。那么,它到底表现如何呢? 妙笔生词智能写歌词软件(veve522)的突出优点在于其便捷性和高效性。对于那些灵感稍…...

力扣hot100-普通数组
文章目录 题目:最大子数组和方法1 动态规划方法2 题目:合并区间题解 题目:轮转数组方法1-使用额外的数组方法2-三次反转数组 题目:除自身以外数组的乘积方法1-用到了除法方法2-前后缀乘积法 题目:最大子数组和 原题链…...

深入浅出Transformer:大语言模型的核心技术
引言 随着自然语言处理(NLP)领域的不断发展,Transformer模型逐渐成为现代大语言模型的核心技术。无论是BERT、GPT系列,还是最近的T5和Transformer-XL,这些模型的背后都离不开Transformer架构。本文将详细介绍Transfor…...

MacOS隐藏文件打开指南
MacOS隐藏文件打开指南 方法一: 直接按下键盘上的【commandshift.】,这时候就可以在mac系统中就会自动显示隐藏的文件夹了 方法二: 在终端查看 ls -la...

grafana数据展示
目录 一、安装步骤 二、如何添加喜欢的界面 三、自动添加注册客户端主机 一、安装步骤 启动成功后 可以查看端口3000是否启动 如果启动了就在浏览器输入IP地址:3000 账号密码默认是admin 然后点击 log in 第一次会让你修改密码 根据自定义密码然后就能登录到界面…...

53-4 内网代理6 - frp搭建三层代理
前提:53-3 内网代理5 - frp搭建二级代理-CSDN博客 三级网络代理 在办公区入侵后,发现需要进一步渗透核心区网络(192.168.60.0/24),并登录域控制器的远程桌面。使用FRP在EDMZ区、办公区与核心区之间建立三级网络的SOCKS5代理,以便访问核心区的域控制器。 VPS上的FRP服…...

SQLite 命令行客户端 + HTA 实现简易UI
SQLite 命令行客户端 HTA 实现简易UI SQLite 客户端.hta目录结构参考资料 仅用于探索可行性,就只实现了 SELECT。 SQLite 客户端.hta <!DOCTYPE html> <html> <head><meta http-equiv"Content-Type" content"text/html; cha…...

TikTok小店推出“百万英镑俱乐部”,实力宠卖家!
TikTok Shop近期在英国市场重磅推出了“百万英镑俱乐部”激励计划,这一举措旨在通过一系列诱人福利,助力商家在TikTok平台上实现销售飞跃。该计划不仅彰显了TikTok Shop对于商家成长的深切关怀,更以实际行动诠释了“实力宠卖家”的承诺。 我…...

路径规划 | 基于蚁群算法的三维无人机航迹规划(Matlab)
目录 效果一览基本介绍程序设计参考文献 效果一览 基本介绍 基于蚁群算法的三维无人机航迹规划(Matlab)。 蚁群算法(Ant Colony Optimization,ACO)是一种模拟蚂蚁觅食行为的启发式算法。该算法通过模拟蚂蚁在寻找食物时…...
.Net C#执行JavaScript脚本
文章目录 前言一、安装二、执行 JavaScript 脚本三、与脚本交互四、JS 调用 C# 方法五、多线程使用总结 前言 ClearScript 是一个 .NET 平台下的开源库,用于在 C# 和其他 .NET 语言中执行脚本代码。它提供了一种方便和安全的方法来将脚本与应用程序集成,…...

企业应对策略:全面防御.DevicData-P-xxxxxx勒索病毒
引言 在数字化时代,网络安全已成为不可忽视的重要议题。随着互联网的普及,各种网络威胁层出不穷,其中勒索病毒以其独特的攻击方式和巨大的破坏性,给个人用户和企业带来了严重的经济损失和数据安全风险。在众多勒索病毒中ÿ…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
