算法·高精度
高精度算法
- 分为四则运算加减乘除
适用条件
- 都高精度了,肯定时long long都会爆的情况——一般与阶乘有关
注意事项
- 用数组模拟位运算,最后在一起考虑进位
- 注意
res[i+1]+=res[i]/10;是"+="不是=
- 注意
- 两数相加,相乘数组的新长度会变,要正确计算!
- 加法:
len=max(lena,lenb)+1 - 乘法:
len=lena+lenb+1
- 加法:
- 位运算的公式
- 加法:
a[i] += b[i]; - 乘法:
res[i+j-1]+=a[i]*b[j];模拟乘法运算,一个数字乘以行的情况
- 加法:
- 对于阶乘:
- 最好是定义一个类bigInt,便于组织代码
for(int i=2;i<=n;i++){ x*i }利用循环模拟,不建议递归
加法模板
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
string stra, strb;
int a[5009];
int b[5009];
void solve() {cin >> stra >> strb;int lena = stra.size(), lenb = strb.size();for (int i = lena-1; i >= 0; i--) {a[lena - i] = stra[i]-'0';}/*for (int i = lena; i >= 1; i--) {cout << a[i];}cout << endl;*/for (int i = lenb - 1; i >= 0; i--) {b[lenb - i] = strb[i]-'0';}/*for (int i = lenb; i >= 1; i--) {cout << b[i];}cout << endl;*/int len = max(lena, lenb) + 2;for (int i = 1; i <= len; i++) {a[i] += b[i];}//for (int i = len; i >= 1; i--) {// cout << a[i] << " ";//}//cout << endl;for (int i = 1; i <= len; i++) {a[i + 1] += a[i] / 10;a[i] %= 10;}/*for (int i = len; i >= 1; i--) {cout << a[i] << " ";}*/for (; a[len]==0&&len>0;len--);if (len <=1) {cout << 0;return;}for (int i = len; i >= 1; i--) {cout << a[i];}
}
乘法模板
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
string stra, strb;
int a[5009];
int b[5009];
int res[5009];
void solve() {cin >> stra >> strb;int lena = stra.size(), lenb = strb.size();for (int i = lena-1; i >= 0; i--) {a[lena - i] = stra[i]-'0';}for (int i = lenb - 1; i >= 0; i--) {b[lenb - i] = strb[i]-'0';}int len = lena + lenb + 2;for (int i = 1; i <= lena; i++) {for (int j = 1; j <= lenb; j++) {res[i + j - 1] += a[i] * b[j];}}/*for (int i = 1; i <= 10; i++) {cout << res[i] << " ";}cout << endl;*/for (int i = 1; i <= len; i++) {res[i + 1] += res[i] / 10;res[i] %= 10;}/*for (int i = 1; i <= 10; i++) {cout << res[i] << " ";}*//*for (int i = len; i >= 1; i--) {cout << a[i] << " ";}*/for (; res[len]==0&&len>0;len--);if (len <1) {cout << 0;return;}for (int i = len; i >= 1; i--) {cout << res[i];}
}
阶乘模板
using namespace std;
using ll = long long;
int t,n,a,ct;
class bigInt {
public://构造一个类,避免重复开辟新空间int a[5009];int len;bigInt() {memset(a, 0, sizeof(a));a[1] = 1;len = 1;}void operator*(int b) {for (int i = 1; i <= len; i++) {a[i] *= b;}len += b/10+1;//扩容不是固定的+2!!!for (int i = 1; i <= len; i++) {a[i + 1] += a[i] / 10;a[i] %= 10;}for (; a[len]==0; len--);}void print() {for (int i = len; i >= 1; i--) {cout << a[i];}}
};
bigInt number;
void solve() {cin >> t;while (t--) {cin >> n >> a;if (n == 0) {//特判0!=1(也可以不特判)cout << (a == 1 ? 1 : 0); continue;}for (int i = 2; i <= n; i++) {number* i;//原地对number不断发生阶乘运算//你也可以定义=运算符,但是我懒}number.print();cout << endl;}
}
以下均为例题
阶乘数码
题目描述
求 n ! n! n! 中某个数码出现的次数。
输入格式
第一行为 t ( t ≤ 10 ) t(t \leq 10) t(t≤10),表示数据组数。接下来 t t t 行,每行一个正整数 n ( n ≤ 1000 ) n(n \leq 1000) n(n≤1000) 和数码 a a a。
输出格式
对于每组数据,输出一个整数,表示 n ! n! n! 中 a a a 出现的次数。
样例 #1
样例输入 #1
2
5 2
7 0
样例输出 #1
1
2
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int t,n,a,ct;
class bigInt {
public:int a[5009];int len;bigInt() {memset(a, 0, sizeof(a));a[1] = 1;len = 1;}void operator*(int b) {for (int i = 1; i <= len; i++) {a[i] *= b;}len += b/10+1;//扩容不是固定的+2!!!for (int i = 1; i <= len; i++) {a[i + 1] += a[i] / 10;a[i] %= 10;}for (; a[len]==0; len--);}void print() {for (int i = len; i >= 1; i--) {cout << a[i];}}
};
bigInt number;
void solve() {cin >> t;while (t--) {cin >> n >> a;if (n == 0) {cout << (a == 1 ? 1 : 0); continue;}memset(number.a, 0, sizeof(number.a));number.a[1] = 1;number.len = 1;ct = 0;//初始化for (int i = 2; i <= n; i++) {number* i;//不断发生变换}/*number.print();cout << endl;*/for (int i = 1; i <= number.len; i++) {if (number.a[i] == a) {ct++;}}cout << ct<<endl;}
}
signed main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}
相关文章:

算法·高精度
高精度算法 分为四则运算加减乘除 适用条件 都高精度了,肯定时long long都会爆的情况——一般与阶乘有关 注意事项 用数组模拟位运算,最后在一起考虑进位 注意res[i1]res[i]/10; 是""不是 两数相加,相乘数组的新长度会变&…...

Docker搭建kafka+zookeeper以及Springboot集成kafka快速入门
参考文章 【Docker安装部署KafkaZookeeper详细教程】_linux arm docker安装kafka-CSDN博客 Docker搭建kafkazookeeper 打开我们的docker的镜像源配置 vim /etc/docker/daemon.json 配置 { "registry-mirrors": ["https://widlhm9p.mirror.aliyuncs.com"…...

【cocos2dx】【iOS工程】如何保存用户在游戏内的绘画数据,并将数据以图像形式展示在预览界面
【cocos2dx】【iOS工程】如何保存用户在应用内的操作数据,并将数据以图像形式展示在预览界面 设备/引擎:Mac(11.6)/Mac Mini 开发工具:Xcode(15.0.1) 开发需求:如何保存用户在应用…...

拥抱应用创新,拒绝无谓的模型竞争
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

【源码+文档+调试讲解】旅游资源网站
摘 要 本论文主要论述了如何使用JAVA语言开发一个旅游资源网站 ,本系统将严格按照软件开发流程进行各个阶段的工作,采用B/S架构,面向对象编程思想进行项目开发。在引言中,作者将论述旅游资源网站的当前背景以及系统开发的目的&…...

Monaco 多行提示的实现方式
AI 代码助手最近太火爆,国内有模型厂商都有代码助手,代码助手是个比较典型的 AI 应用,主要看前端,后端的模型都差不多,国内外都有专门的代码模型。现在都是集中在 VSCode 和 Idea的插件,本文通过 Monaco 实…...

SpringMVC的架构有什么优势?——表单和数据校验(四)
#SpringMVC的架构有什么优势?——表单和数据校验(四) 前言 关键字: 机器学习 人工智能 AI chatGPT 学习 实现 使用 搭建 深度 python 事件 远程 docker mysql安全 技术 部署 技术 自动化 代码 文章目录 - - - - - 表单数据…...

Linux实战记录
踩坑实录: day2: 最坑:安装UB居然不知道创建文件夹。 1.虚拟机上不了网:多重置几次 网卡 2.Winscp链接主机: 用户名 就是 linux terminal中的 第一个用户名!...

时间、查找、打包、行过滤与指令的运行——linux指令学习(二)
前言:本节内容标题虽然为指令,但是并不只是讲指令, 更多的是和指令相关的一些原理性的东西。 如果友友只想要查一查某个指令的用法, 很抱歉, 本节不是那种带有字典性质的文章。但是如果友友是想要来学习的,…...

android CameraX构建相机拍照
Android CameraX 是一个 Jetpack 支持库,旨在简化相机应用的开发工作。它提供了一致且易用的API接口,适用于大多数Android设备,并可向后兼容至Android 5.0(API级别21)。 CameraX解决了在多种设备上实现相机功能时所遇…...

【普中】基于51单片机的矩阵电子密码锁LCD1602液晶显示 proteus仿真+程序+设计报告+讲解视频
【普中】基于51单片机的矩阵电子密码锁LCD1602液晶显示设计 1.主要功能:讲解视频:2.仿真3. 程序代码4. 设计报告5. 设计资料内容清单&&下载链接资料下载链接: 【普中】基于51单片机的矩阵电子密码锁LCD1602液晶显示设计 ( proteus仿真…...

工厂水电燃气表流量计等能耗计量仪表非侵入式拍照抄表的方案
在企业园区、工厂等企事业单位,传统的手动抄表方式已逐渐不能满足现代化、信息化管理的需求。为了提高抄表工作的效率,减少人工操作的误差,同时保障数据的安全性和实时性,我们提出了拍照采集抄表方案。本方案旨在通过拍照的方式&a…...

LLM大模型应用中的安全对齐的简单理解
LLM大模型应用中的安全对齐的简单理解 随着人工智能技术的不断发展,大规模语言模型(如GPT-4)的应用越来越广泛。为了保证这些大模型在实际应用中的性能和安全性,安全对齐(Safe Alignment)成为一个重要的概…...

clickhouse-jdbc-bridge rce
clickhouse-jdbc-bridge 是什么 JDBC bridge for ClickHouse. It acts as a stateless proxy passing queries from ClickHouse to external datasources. With this extension, you can run distributed query on ClickHouse across multiple datasources in real time, whic…...

java中Comparator函数的用法实例?
在Java中,Comparator接口用于比较两个对象的顺序,常用于集合的排序。自Java 8开始,Comparator接口得到了增强,提供了许多默认方法,使得排序逻辑更加灵活和强大。下面将通过几个实例来展示Comparator的用法。 示例1&am…...

mysql实战入门-基础篇
目录 1、MySQL概述 1.1、数据库相关概念 1.2、MySQL数据库 1.2.1、版本 1.2.2、下载 1.2.3、安装 输入MySQL中root用户的密码,一定记得记住该密码 1.2.4、启动停止 1.2.5、客户端连接 1.2.6、数据模型 2、SQL 2.1、SQL通用语法 2.2、SQL分类 2.3、DDL 2.3.1、数据…...
阶段三:项目开发---民航功能模块实现:任务24:航空实时监控
任务描述 内 容:地图展示、飞机飞行轨迹、扇区控制。航空实时监控,是飞机每秒发送坐标,经过终端转换实时发送给塔台,为了飞机位置的精准度,传输位置的密度很大,在地图位置显示不明显。本次为了案例展示效…...

手机容器化 安装docker
旧手机-基于Termux容器化 1、安装app 在手机上安装Termux或ZeroTermux(Termux扩展) 1.1 切换源 注:可以将termux进行换源,最好采用国内源,例如:清华源等 更新包列表和升级包(可选࿰…...
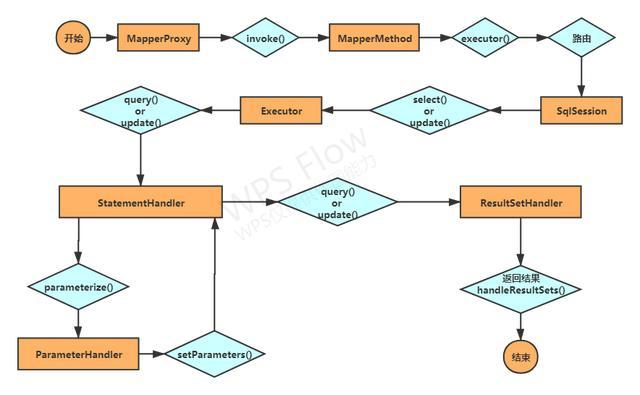
科普文:深入理解Mybatis
概叙 (1) JDBC JDBC(Java Data Base Connection,java数据库连接)是一种用于执行SQL语句的Java API,可以为多种关系数据库提供统一访问,它由一组用Java语言编写的类和接口组成.JDBC提供了一种基准,据此可以构建更高级的工具和接口,使数据库开发人员能够编写数据库应用程序。 优点…...

称重传感器有哪些种类
有关称重传感器的知识,称重传感器是众多传感器产品中的一种,也是很常用的传感器之一,那么称重传感器有哪些种类,称重传感器的分类方式是什么样的,一起来了解下。 称重传感器的分类 主要有六种称重传感器类型…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
