堆结构的两个应用
堆排序
堆结构很大的一个用处,就是用于堆排序了,堆排序的时间复杂度是O(n∗log2n)O(n*log_2n)O(n∗log2n)量级的,在众多排序算法中所处的地位也是高手级别的了。
但很多人在使用堆排序的时候,首先认为我必须得有一个堆数据结构才行,如下面代码这样:
//堆的结构定义
typedef int HDataType;
typedef struct Heap
{HDataType* a;//堆数据在物理上使用数组进行存储int size;//标记堆数据的有效个数int capacity;//标记堆空间的容量大小
}Hp;
Hp hp;//定义一个堆数据结构
HeapInit(&hp);//初始化堆int a[] = { 27,15,19,18,28,34,65,49,25,37 };
for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
{//为了进行堆排序,先将要排序的数据都push进堆数据结构中HeapPush(&hp, a[i]);
}
//此时,堆数据结构中存着一份要排序的数据,数组a里面存着一份要排序的数据int i = 0;
while (!HeapEmpty(&hp))
{//不断取堆顶元素,放进数组a中,当堆为空时,数组a就有序了a[i++] = HeapTop(&hp);HeapPop(&hp);
}
HeapDestroy(&hp);
这种堆排序方法也能排序,但未免有些不尽人意,没能充分利用堆的优势。
虽然时间复杂度达到了O(n∗log2n)O(n*log_2n)O(n∗log2n),但额外的空间复杂度是O(n)O(n)O(n),因为需要先创建一个堆数据结构出来,用于存放要排序的数据。
如果是像C++的STL那样堆结构通过容器封装,可以直接拿来用的话还好说;但像C语言那样没有现成的堆数据结构可以用,那要想进行堆排序的话,还得自己先写一个堆数据结构出来,劳神费力,搞得复杂了。
所以,有没有什么更好的方法呢?
其实,细心观察不难发现,堆数据结构中的数据在物理上是使用数组进行存储的,而我们需要进行排序的数据也是存放在一个a数组中的,那我们是不是直接可以在a数组中进行堆排序了。
我们可以将a数组从逻辑上看成一棵完全二叉树,需要将其进行调整,以符合堆的结构。此时会涉及到堆的两种调整方式,这两种调整方式都能将一棵完全二叉树调整成堆结构:一个是向上调整建堆,一个是向下调整建堆。具体详情可参看阿顺的这篇博文堆的结构与实现。博文里面对于向上调整建堆和向下调整建堆都给出了时间复杂度的相应计算,最后发现,向下调整建堆的时间复杂度是O(n)O(n)O(n),向上调整建堆的时间复杂度是O(n∗log2n)O(n*log_2n)O(n∗log2n),所以通过比较,我们自然会选择时间复杂度更优的那个,也就是向下调整建堆了。
//向下调整建堆:O(n)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{AdjustDown(a, n, i);
}
此时,a数组已然从一棵完全二叉树蜕变成了一个堆结构。
好了,有了堆结构,如何在a数组上进行操作,将其变得有序呢?这似乎又是个难题。
细心的同学此时又发现,在阅读堆的结构与实现时看到,在介绍堆的向下调整时,首先说到了,堆的删除操作。在删除堆顶数据时,并不是像顺序表一样进行的是覆盖删除,而是用到了一种巧妙的交换操作。堆的删除操作与堆的向下调整天生不可分割 。沿着这个思路,是否能将这种交换操作延伸到堆排序中呢?
答案是肯定的。
//end等于数组数组最后一个元素的下标
int end = n - 1;
while (end > 0)
{//将堆顶数据和堆的最后一个数据进行交换Swap(&a[0], &a[end]);//end此时代表的是数组中的数据个数(n-1)个,将最后一个数据排除在外AdjustDown(a, end, 0);//end减一,end又成了最后一个要调整的数据的下标--end;
}
所以整个思想转换成代码如下:
void HeapSort(int* a, int n)
{//先向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}//O(N*logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}
void HeapSortTest()
{int a[] = { 27,15,19,18,28,34,65,49,25,37 };HeapSort(a, sizeof(a) / sizeof(int));
}
要注意的是,通过以上思路分析,可以发现,要想排升序,需要建大堆,排降序,需要建小堆。
Top-K问题
Top-K问题在实际生活中,还是很常见的。比如说:中国排名前10的大学,世界前500强企业,王者荣耀国服李白等等。
但很多时候,对于Top-K问题,能想到的最简单直接的方式就是排序了。结合问题所需是前K个最小的数据,还是前K个最大的数据,来决定是排升序还是排降序。但是,如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的处理方式还是用堆来解决。
根据上面对于堆排序的讲解,我们这里就可以很好的理解Top-K问题了。
有老铁说,我先用a数组中的前k个数据建个堆,再通过循环将前k个数据之后的数据,一个个都和堆顶数据进行比较,根据问题需求先进行替换,再进行堆的调整,最后这一折腾下来,堆中不就保留了我所想要的数据了吗。
但是,我想说的是,在了解上面的堆排序之后,我们能不能就在原地操作呢?
没错,我们就是要主观地认为,a数组中前k个数据就是我们想要的数据。先将前k个数据调整成堆,在通过循环将前k个数据之后的数据,一个个都和堆顶数据(a[0])进行比较,根据问题需求先进行替换,再进行堆顶数据的向下调整,最后循环完毕,a数组中的前k个数据也就是我们所需要的了。
根据思路,可以写出代码如下:
void TopKFind(int* a, int n, int k)
{assert(a != NULL);int* KMinHeap = a;//先将前k个数据调整成堆for (int i = (k - 1 - 1) / 2; i >= 0; --i){AdjustDown(KMinHeap, k, i);}//将之后的数据与堆顶数据进行比较for (int i = k; i < n; ++i){//此处寻找的是前k个最大的数据if (KMinHeap[0] < a[i]){KMinHeap[0] = a[i];AdjustDown(KMinHeap, k, 0);}}
}
最后,需要注意的是,寻找前k个最小的数据,需要建大堆,寻找前k个最大的数据,需要建小堆。至于是要前k个最小的数据,还是前k个最大的数据,可以根据自己的需求,将判断条件略做更改即可。
相关文章:

堆结构的两个应用
堆排序 堆结构很大的一个用处,就是用于堆排序了,堆排序的时间复杂度是O(n∗log2n)O(n*log_2n)O(n∗log2n)量级的,在众多排序算法中所处的地位也是高手级别的了。 但很多人在使用堆排序的时候,首先认为我必须得有一个堆数据结构…...

Java中的 static
1 static 静态变量 1.1 静态变量的使用 static变量也称作静态变量,也叫做类变量 静态变量被所有的对象所共享,在内存中只有一个副本 当且仅当在类初次加载时会被初始化 静态变量属于类 通过类名就可以直接调用静态变量 也可以通过对象名.静态变量…...

基于Vision Transformer的图像去雾算法研究与实现(附源码)
基于Vision Transformer的图像去雾算法研究与实现 0. 服务器性能简单监控 \LOG_USE_CPU_MEMORY\文件夹下的use_memory.py文件可以实时输出CPU使用率以及内存使用率,配合nvidia-smi监控GPU使用率 可以了解服务器性能是否足够;运行时在哪一步使用率突然…...

服务器相关常用的命令
cshell语法 https://www.doc88.com/p-4985161471426.html domainname命令 1)查看当前系统域名 domainname2)设置并查看当前系统域名 domainname example.com3)显示主机ip地址 domainname -Iwhich命令 which 系统命令在 PATH 变量指定的…...
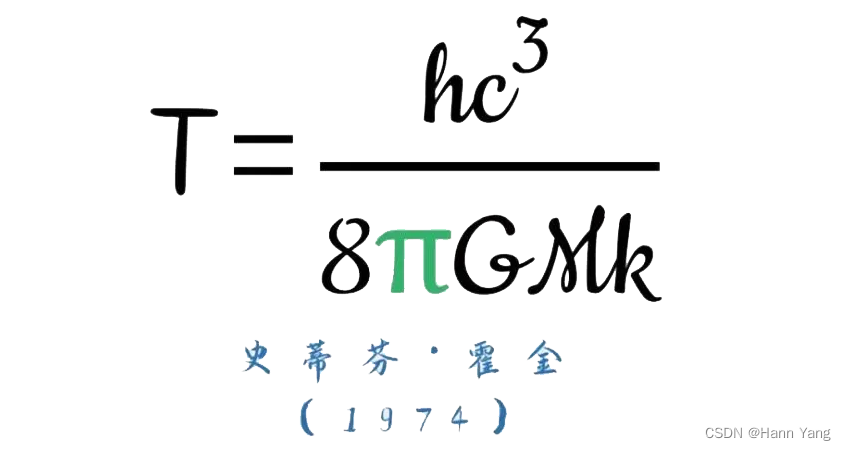
今天是国际数学日,既是爱因斯坦的生日又是霍金的忌日
目录 一、库函数计算 π 二、近似值计算 π 三、无穷级数计算 π 四、割圆术计算 π 五、蒙特卡罗法计算 π 六、计算800位精确值 从2020年开始,每年的3月14日又被定为国际数学日,是2019年11月26日联合国教科文组织第四十届大会上正式宣布…...

Qt Quick - StackLayout 堆布局
StackLayout 堆布局一、概述二、attached 属性三、例子1. 按钮切换 StackLayout 页面一、概述 StackLayout 其实就是说,在同一个时刻里面,只有一个页面是展示出来的,类似QStackWidget 的功能,主要就是切换界面的功能。这个类型我…...
C/C++网络编程笔记Socket
https://www.bilibili.com/video/BV11Z4y157RY/?vd_sourced0030c72c95e04a14c5614c1c0e6159b上面链接是B站的博主教程,源代码来自上面视频,侵删,这里只是做笔记,以供复习和分享。上一篇博客我记录了配置环境并且跑通了࿰…...

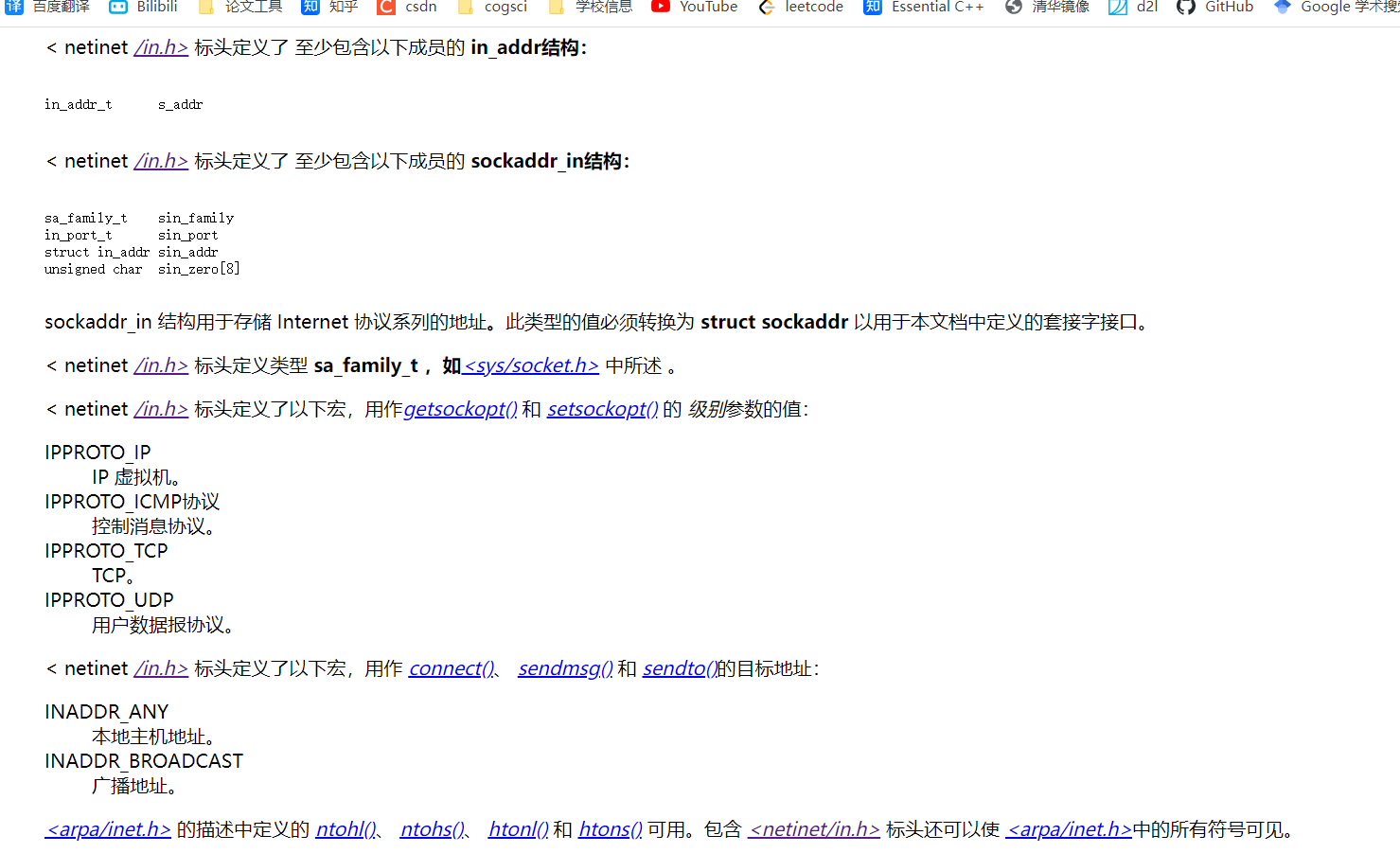
RK3568平台开发系列讲解(网络篇)什么是Socket套接字
🚀返回专栏总目录 文章目录 一、什么是socket ?二、socket 理解为电话机三、socket 的发展历史四、套接字地址格式4.1、通用套接字地址格式4.2、IPv4 套接字格式地址4.3、IPv6 套接字地址格式4.4、几种套接字地址格式比较沉淀、分享、成长,让自己和他人都能有所收获!😄 …...
网络安全竞赛试题——渗透测试解析(详细))
2022年全国职业院校技能大赛(中职组)网络安全竞赛试题——渗透测试解析(详细)
渗透测试 任务环境说明: 服务器场景:Server9服务器场景操作系统:未知(关闭连接)系统用户名:administrator密码:123456通过本地PC中渗透测试平台Kali对靶机场景进行系统服务及版本扫描渗透测试,以xml格式向指定文件输出信息(使用工具Nmap),将以xml格式向指定文件输出…...

尚融宝03-mybatis-plus基本CRUD和常用注解
目录 一、通用Mapper 1、Create 2、Retrieve 3、Update 4、Delete 二、通用Service 1、创建Service接口 2、创建Service实现类 3、创建测试类 4、测试记录数 5、测试批量插入 三、自定义Mapper 1、接口方法定义 2、创建xml文件 3、测试条件查询 四、自定义Serv…...

vue多行显示文字展开
这几天项目里面有一个需求,多行需要进行展开文字,类似实现这种效果 难点就在于页面布局 一开始就跟无头苍蝇似的,到处百度 ,后面发现网上的都不适合自己,最终想到了解决方案 下面是思路: 需求是超过3行&a…...
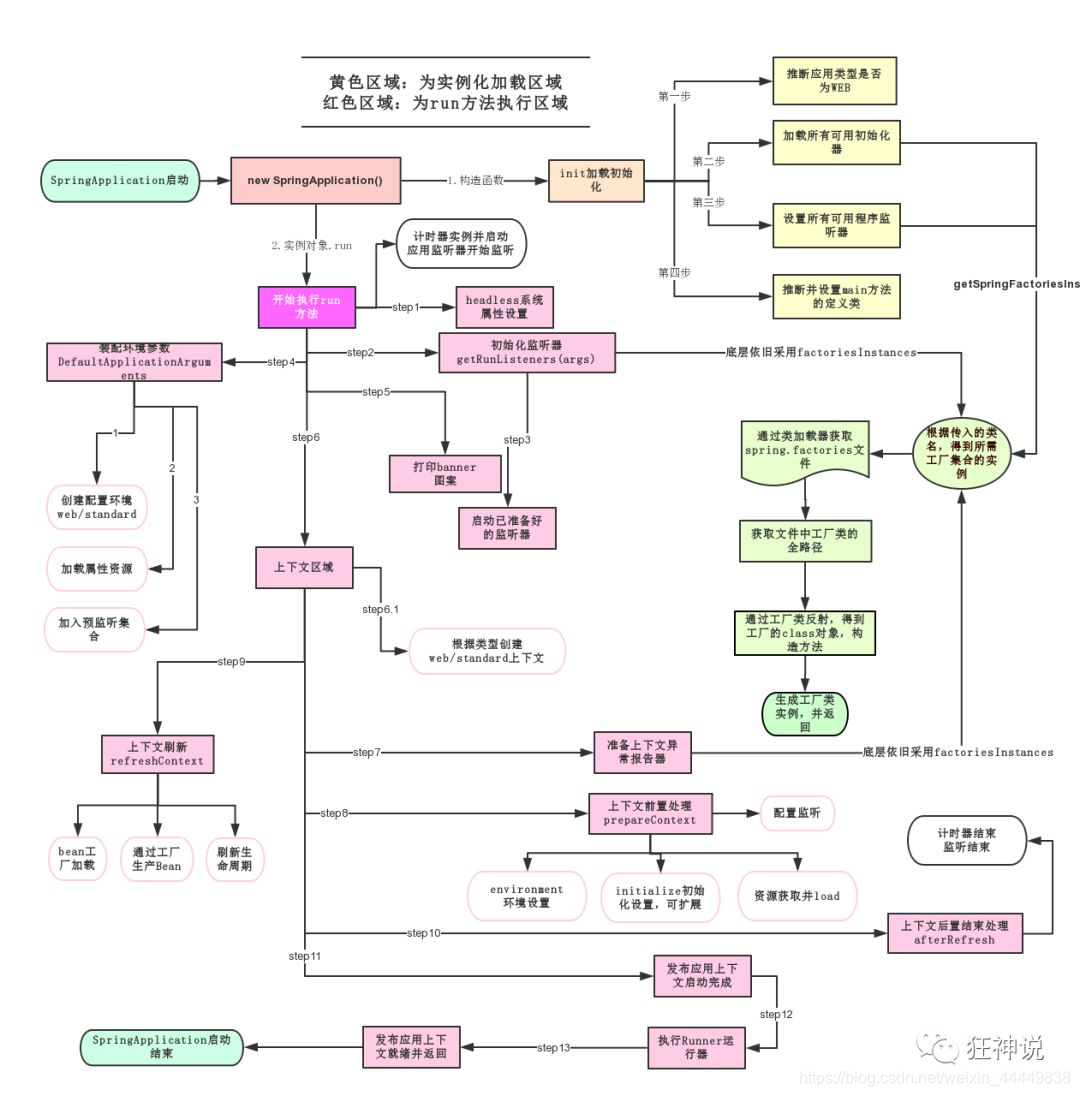
SpringBoot:SpringBoot 的底层运行原理解析
声明原文出处:狂神说 文章目录1. pom.xml1 . 父依赖2 . 启动器 spring-boot-starter2. 主启动类的注解1. 默认的主启动类2. SpringBootApplication3. ComponentScan4. SpringBootConfiguration5. SpringBootApplication 注解6. spring.factories7. 结论8. 简单图解3…...

哪些场景会产生OOM?怎么解决?
文章目录 堆内存溢出方法区(运行时常量池)和元空间溢出直接内存溢出栈内存溢出什么时候会抛出OutOfMemery异常呢?初看好像挺简单的,其实深究起来考察的是对整个JVM的了解,而这个问题从网上可以翻到一些乱七八糟的答案,其实在总结下来基本上4个场景可以概括下来。 堆内存溢出…...

金三银四、金九银十 面试宝典 Spring、MyBatis、SpringMVC面试题 超级无敌全的面试题汇总(超万字的面试题,让你的SSM框架无可挑剔)
Spring、MyBatis、SpringMVC 框架 - 面试宝典 又到了 金三银四、金九银十 的时候了,是时候收藏一波面试题了,面试题可以不学,但不能没有!🥁🥁🥁 一个合格的 计算机打工人 ,收藏夹里…...
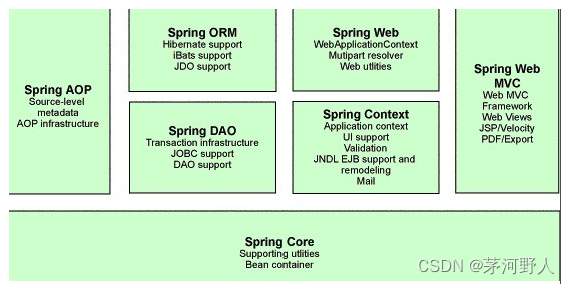
JAVA开发(Spring框架详解)
javaweb项目几乎已经离不开spring框架了,spring 是一个典型的分层架构框架,它包含一系列的功能并被分为多个功能模块,springboot对spring框架又做了一层封装,以至于很多人对原来的spring框架越来越不了解。 要谈Spring的历史&…...

自学大数据第八天~HDFS命令(二)
嗨喽,好久不见,最近抽空复习了一下hadoop,书读百遍,其意自现这句话还真是; 继续学习HDFS常用命令 改变文件 拥有者~chown hdfs dfs -chown -R hadoop /user/hadoop使用 -R 将使改变在目录结构下递归进行。命令的使用者必须是超级用户。 改变文件所属组-chgrp hdfs dfs -chgr…...
贪心算法(几种常规样例)
贪心算法(几种常规样例) 贪心算法,指在对问题进行求解的时候,总是做出当前看来是最好的选择。也就是说不从整体上最优上考虑,算法得到的结果是某种意义上的局部最优解 文章目录贪心算法(几种常规样例&…...

【数据结构】基础知识总结
系列综述: 💞目的:本系列是个人整理为了数据结构复习用的,由于牛客刷题发现数据结构方面和王道数据结构的题目非常像,甚至很多都是王道中的,所以将基础知识进行了整理,后续会将牛客刷题的错题一…...
宣布推出 .NET 社区工具包 8.1!
我们很高兴地宣布 .NET Community Toolkit 8.1 版正式发布!这个新版本包括呼声很高的新功能、bug 修复和对 MVVM 工具包源代码生成器的大量性能改进,使开发人员在使用它们时的用户体验比以往更好! 就像在我们之前的版本中一样,我…...

ChatGPT解开了我一直以来对自动化测试的疑惑
目录 前言 与ChatGPT的对话 什么是自动化测试,我该如何做到自动化测试,或者说需要借助什么工具可以做到自动化测试? 自动化测试如何确保数据的准确性 自动化测试是怎么去验证数据的 如何通过断言验证数据 自动化测试有哪些验证工具可以验证数据 总结 前言…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...
