MT3046 愤怒的象棚


思路:
a[]存愤怒值;b[i]存以i结尾的,窗口里的最大值;c[i]存以i结尾的,窗口里面包含✳的最大值。
(✳为新大象的位置)
例:1 2 3 4 ✳ 5 6 7 8 9
则ans的计算公式=b3+b4+c4+c5+c6+b7+b8+b9;
b3为max[1 2 3]; b4为max[2 3 4];
c4为max[3 4 ✳]; c5为max[4 ✳ 5]; c6为max[✳ 5 6];
b7为max[5 6 7]; b8为max[6 7 8]; b9为max[7 8 9];
由此可以归纳得到一个公式:n个数,每个窗口长度为m,遍历到i时,ans可以分成三段:①[b(m)+b(m+1)+...+b(i-1)] + ②[c(i-1)+c(i)+...+c(i+m-2)] + ③[b(i+m-1)+...+b(n)]
(求max[]使用单调队列来求,求ans用前缀和)
ans=sumb[i-1]+sumc[i+m-2]-sumc[i-2]+sumb[n]-sumb[i+m-2]
但是还有ans某部分不存在的情况:
当i<=m时,此时①不存在,即ans=sumc[i+m-2]+sumb[n]-sumb[i+m-2]
若i>=n-m+2时,此时③不存在,,即ans=sumb[i-1]+sumc[n]-sumc[i-2]
当i>m&&i<n-m+2时,ans=sumb[i-1]+sumc[i+m-2]-sumc[i-2]+sumb[n]-sumb[i+m-2]
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 5e6 + 10;
int n, m, A, ans = 0;
int a[N], b[N], c[N];
int sumc[N], sumb[N];
void getmax(int n, int m)
{deque<int> q;for (int i = 1; i <= n; i++){if (!q.empty() && q.front() <= i - m)q.pop_front();while (!q.empty() && a[i] >= a[q.back()])q.pop_back();q.push_back(i);if (i >= m){b[i] = a[q.front()];sumb[i] = sumb[i - 1] + b[i];}}
}
void getmax2(int n, int m)
{deque<int> q;for (int i = 1; i <= n; i++){if (!q.empty() && q.front() <= i - m)q.pop_front();while (!q.empty() && a[i] >= a[q.back()])q.pop_back();q.push_back(i);if (i >= m){c[i] = max(A, a[q.front()]);sumc[i] = sumc[i - 1] + c[i];}}
}int main()
{cin >> n >> m >> A;for (int i = 1; i <= n; i++){cin >> a[i];}getmax(n, m); // 求b[]getmax2(n, m - 1); // 求c[]for (int i = 1; i <= n + 1; i++){if (i <= m){ans = max(ans, sumc[i + m - 2] + sumb[n] - sumb[i + m - 2]);}else if (i >= n - m + 2){ans = max(ans, sumb[i - 1] + sumc[n] - sumc[i - 2]);}else{ans = max(ans, sumb[i - 1] + sumc[i + m - 2] - sumc[i - 2] + sumb[n] - sumb[i + m - 2]);}}cout << ans;return 0;
}相关文章:

MT3046 愤怒的象棚
思路: a[]存愤怒值;b[i]存以i结尾的,窗口里的最大值;c[i]存以i结尾的,窗口里面包含✳的最大值。 (✳为新大象的位置) 例:1 2 3 4 ✳ 5 6 7 8 9 则ans的计算公式b3b4c4c5c6b7b8b9…...
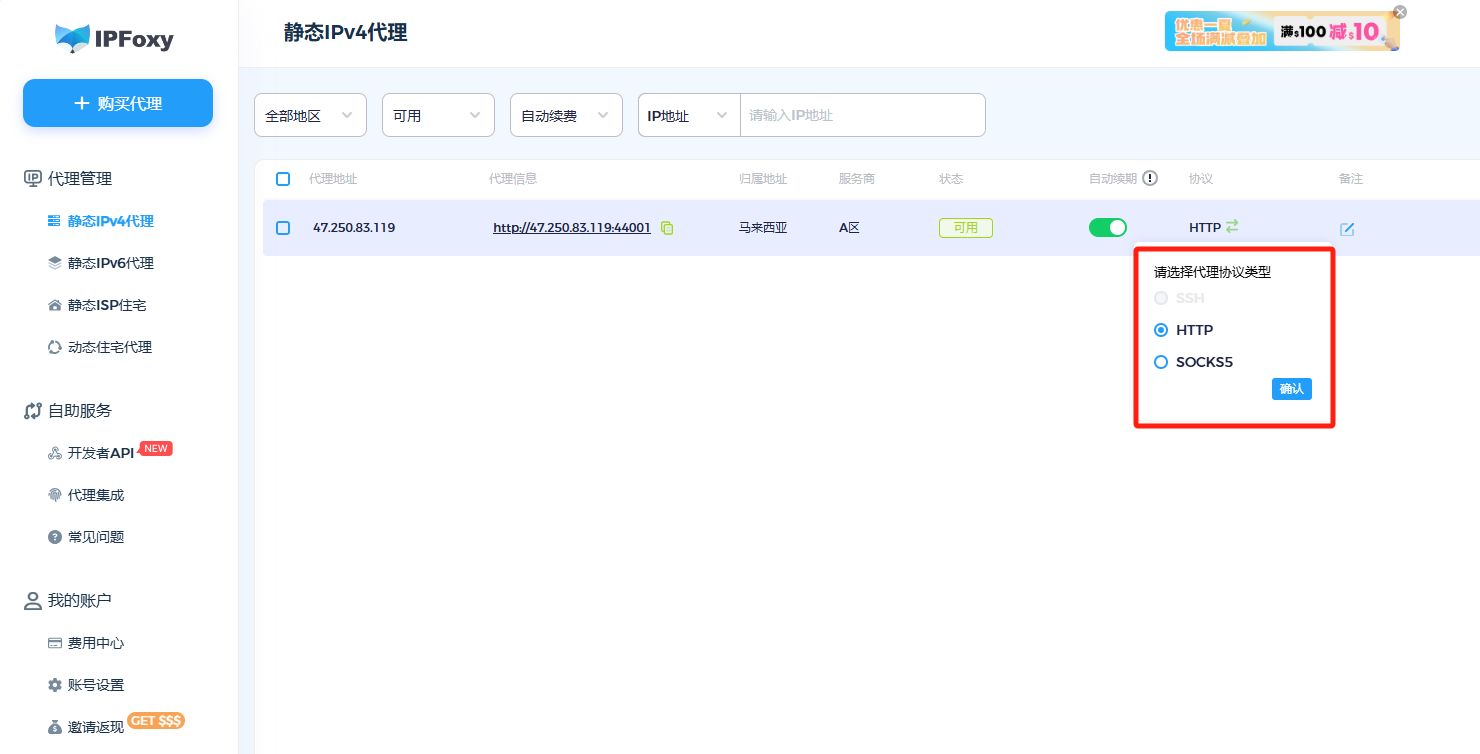
深入了解代理IP常见协议:区别与选择
代理服务器在网络使用中扮演着重要的角色,是您设备和互联网之间的中间层。它不仅可以增强网络访问的安全性和隐私保护,还可以提供许多灵活的应用。使用代理时,不同的协议类型对数据交换具有不同的规则和特征。常见的代理协议包括HTTP代理、HT…...

【Linux 线程】线程的基本概念、LWP的理解
文章目录 一、ps -L 指令🍎二、线程控制 一、ps -L 指令🍎 🐧 使用 ps -L 命令查看轻量级进程信息;🐧 pthread_self() 用于获取用户态线程的 tid,而并非轻量级进程ID;🐧 getpid() 用…...
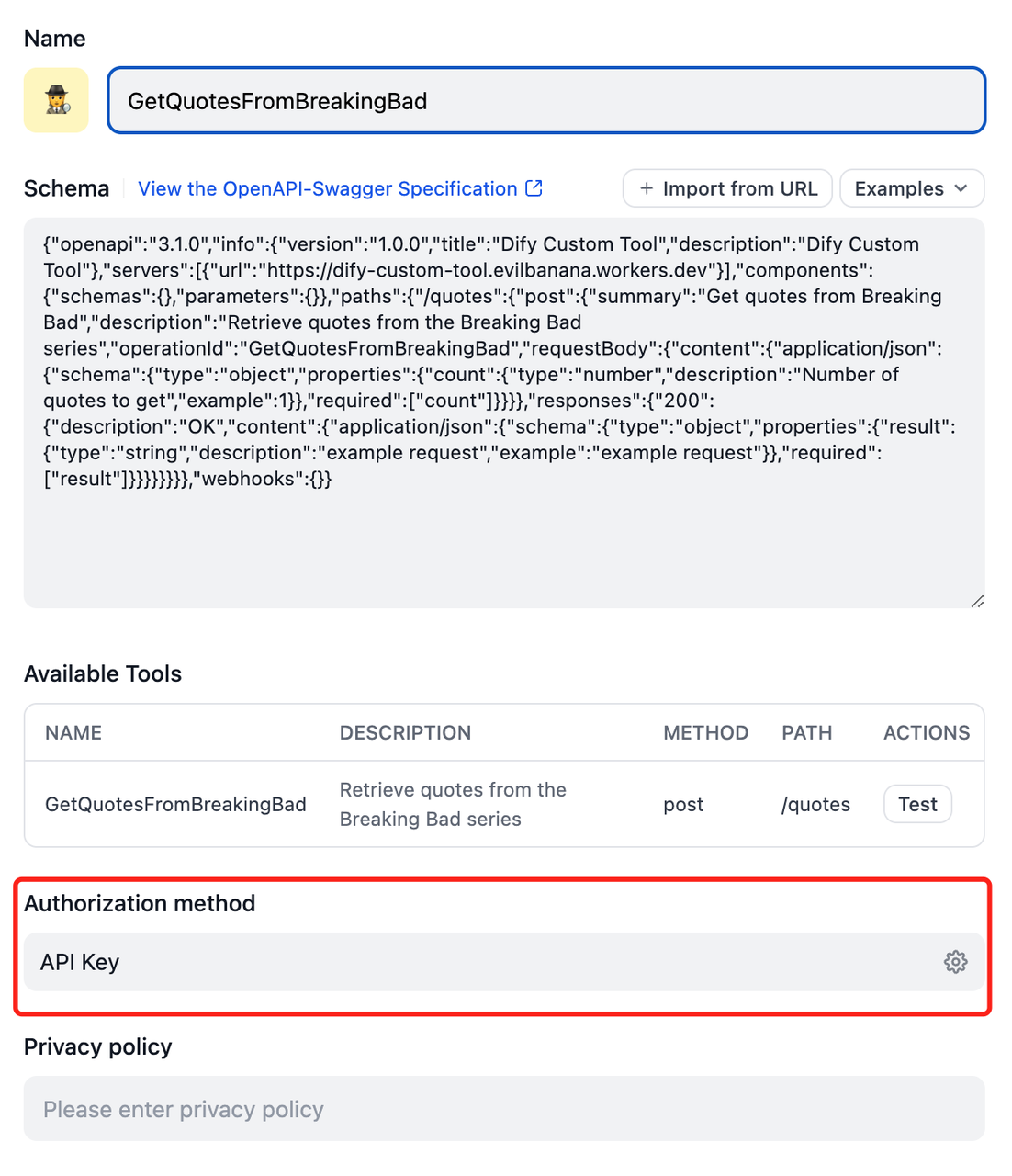
Dify中的工具
Dify中的工具分为内置工具(硬编码)和第三方工具(OpenAPI Swagger/ChatGPT Plugin)。工具可被Workflow(工作流)和Agent使用,当然Workflow也可被发布为工具,这样Workflow(工…...

在Visutal Studio 2022中完成D3D12初始化
在Visutal Studio 2022中完成DirectX设备初始化 1 DirectX121.1 DirectX 简介1.2 DirectX SDK安装2 D3D12初始化2.1 创建Windwos桌面项目2.2 修改符合模式2.3 下载d3dx12.h文件2.4 创建一个异常类D3DException,定义抛出异常实例的宏ThrowIfFailed3 D3D12的初始化步骤3.1 初始化…...

MobaXterm工具
MobaXterm 是一个增强型的 Windows 终端。其为 Windows 桌面提供所有重要的远程网络终端工具(如 SSH、X11、RDP、VNC、FTP、SFTP、Telnet、Serial、Mosh、WSL 等),和 Unix 命令(如 bash、ls、cat、sed、grep、awk、rsync 等&#…...

二分图练习
对于二分图我们可以用染色法 #include<bits/stdc.h> using namespace std;#define int long long const int N 2e65; int e[N],ne[N],h[N],idx 0; int colo[N]; int num 0;void add(int x,int y){e[idx] y;ne[idx] h[x];h[x] idx; } void dfs(int nod,int c){colo…...

创新设计策略:提升大屏幕可视化设计效果的关键方法
随着科技的不断发展和数据量的快速增长,数据可视化大屏在各个行业中的应用越来越广泛,可以帮助人们更好地理解和分析数据,可视化大屏设计也因此成了众多企业的需求。但很多设计师对可视化大屏设计并不了解,也不知道如何制作可视化…...

论文 | Chain-of-Thought Prompting Elicits Reasoningin Large Language Models 思维链
这篇论文研究了如何通过生成一系列中间推理步骤(即思维链)来显著提高大型语言模型进行复杂推理的能力。论文展示了一种简单的方法,称为思维链提示,通过在提示中提供几个思维链示例来自然地激发这种推理能力。 主要发现࿱…...

[机器学习]-人工智能对程序员的深远影响——案例分析
机器学习和人工智能对未来程序员的深远影响 目录 机器学习和人工智能对未来程序员的深远影响1. **自动化编码任务**1.1 代码生成1.2 自动调试1.3 测试自动化 2. **提升开发效率**2.1 智能建议2.2 项目管理 3. **改变编程范式**3.1 数据驱动开发 4. **职业发展的新机遇**4.1 AI工…...

AI学习环境 没有更好的替代 - (Google)Drive + Colab
在开始正题前,请容许我做一番回顾,并夹带一点点私货(谷歌扛旗的开源精神还没有死,并且会是未来的举足轻重的力量) 卧龙凤雏,一时瑜亮。一切的缘起应该是世纪初的门户网站乱战。 彼时,谷歌是从…...

【观成科技】Websocket协议代理隧道加密流量分析与检测
Websocket协议代理隧道加密流量简介 攻防场景下,Websocket协议常被用于代理隧道的搭建,攻击者企图通过Websocket协议来绕过网络限制,搭建一个低延迟、双向实时数据传输的隧道。当前,主流的支持Websocket通信代理的工具有…...

DangerWind-RPC-framework---三、服务端下机
当一台机器下线时,面临很多问题:如何将其从注册中心下线?如何清理释放资源?客户端拉取服务列表时也使用了本地缓存,如何及时更新本地缓存? 服务端机器的优雅下线需要使用ShutdownHook,这相当于添…...

基于Make的c工程No compilation commands found报错
由于安装gcc时只安装了build-essential,没有将其添加到环境变量中,因此打开Make工程时,CLion会产生如下错误: 要解决这个问题,一个方法是将GCC添加到环境变量中,但是这个方法需要修改至少两个配置文件&…...

c++:面向对象的继承特性
什么是继承 (1)继承是C源生支持的一种语法特性,是C面向对象的一种表现 (2)继承特性可以让派生类“瞬间”拥有基类的所有(当然还得考虑权限)属性和方法 (3)继承特性本质上是为了代码复用 (4)类在C编译器的内部可以理解为结构体,派…...

skywalking-2-客户端-php的安装与使用
skywalking的客户端支持php,真的很棒。 官方安装文档:https://skywalking.apache.org/docs/skywalking-php/next/en/setup/service-agent/php-agent/readme/ 前置准备 本次使用的php版本是8.2.13: php -v PHP 8.2.13 (cli) (built: Nov 21 2023 09:5…...

图文讲解IDEA如何导入JDBC驱动包
前言 学习JDBC编程,势必要学会如何导入驱动包,这里笔者用图文的方式来介绍 视频版本在这里 50秒教你怎么导入驱动包然后进行JDBC编程的学习_哔哩哔哩_bilibili 忘记录音频了,大伙凑合着看 下载驱动包 https://mvnrepository.com/artifact/mysql/mysql-connector-java 去中…...
java.lang.NullPointerException: null cannot be cast to non-null type kotlin.Int
java.lang.NullPointerException: null cannot be cast to non-null type kotlin.Int fun main(args: Array<String>) {var any1: Any?any1 nullval n1 any1 as? Int ?: -2024println(n1)kotlin.runCatching {var any2: Any?any2 nullval n2 any2 as Intprintln(…...

scrapy写爬虫
Scrapy是一个用于爬取网站数据并提取结构化信息的Python框架 一、Scrapy介绍 1.引擎(Engine) – Scrapy的引擎是控制数据流和触发事件的核心。它管理着Spider发送的请求和接收的响应,以及处理Spider生成的Item。引擎是Scrapy运行的驱动力。…...

Mybatis study
一、Mybatis Plus mybatis-plus指定实体类字段不查询 加标签 TableField(exist false) Spring Data Jpa学习 干我们这行,啥时候懈怠,就意味着长进的停止,长进的停止就意味着被淘汰,只能往前冲,直到凤凰涅槃的一天&am…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

【Qt】控件 QWidget
控件 QWidget 一. 控件概述二. QWidget 的核心属性可用状态:enabled几何:geometrywindows frame 窗口框架的影响 窗口标题:windowTitle窗口图标:windowIconqrc 机制 窗口不透明度:windowOpacity光标:cursor…...

Springboot 高校报修与互助平台小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,高校报修与互助平台小程序被用户普遍使用,为…...

基于Java项目的Karate API测试
Karate 实现了可以只编写Feature 文件进行测试,但是对于熟悉Java语言的开发或是测试人员,可以通过编程方式集成 Karate 丰富的自动化和数据断言功能。 本篇快速介绍在Java Maven项目中编写和运行测试的示例。 创建Maven项目 最简单的创建项目的方式就是创建一个目录,里面…...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...

[10-1]I2C通信协议 江协科技学习笔记(17个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17...
