力扣 hot100 -- 动态规划(下)
目录
💻最长递增子序列
AC 动态规划
AC 动态规划(贪心) + 二分
🏠乘积最大子数组
AC 动规
AC 用 0 分割
🐬分割等和子集
AC 二维DP
AC 一维DP
⚾最长有效括号
AC 栈 + 哨兵
💻最长递增子序列
300. 最长递增子序列 - 力扣(LeetCode)
子序列:不用连续
子串:要求连续
AC 动态规划
时间 O(n^2)
/*
dp[i] : 第 i 个元素结尾的最长子序列长度(下标0开始)
dp[i] = max(dp[i], dp[j] + 1)
初始化 : dp[i] = 1
*/
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n + 1, 1);for (int i = 1; i < n; ++i)for (int j = 0; j < i; ++j) if (nums[j] < nums[i])dp[i] = max(dp[i], dp[j] + 1);int ans = 1;for (auto x : dp)ans = max(ans, x);return ans;}
};AC 动态规划(贪心) + 二分
二分实现 O(logn) 查找,为了使用二分,我们需要让 dp[] 数组有序,所以需要改变 dp[] 数组的含义(状态)
贪心策略:tails 中存储的元素越小,上升的子序列越长
举例解释
nums[] = {7, 8, 9, 1, 2, 3, 4, 5};
遍历完 7 8 9 后 tails[] = {7, 8, 9};
接着遍历到 1,那么二分查找 tails[],找到第一个比 tails 大的位置,即 7,替换后变成
tails[] = {1, 8, 9};
如果没有比当前 nums[] 值大的元素,直接加到后面
最后输出 tails[] 长度,就是最长上升子序列长度
时间 O(nlogn)
/*
tails[i] : 长度 i+1 子序列的尾部元素
1)nums[] 中当前元素 x > tails.back(), x 插入 tails 最后
2)否则, 二分查找 tails[] 中第一个 > x 的元素, 替换成 x
最后返回 tails[] 大小
*/
class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> tails;tails.push_back(nums[0]);for (auto x : nums) {if (x > tails.back()) {tails.push_back(x);continue;}int l = 0, r = tails.size() - 1;while (l < r) {int mid = (l + r) >> 1;if (tails[mid] < x)l = mid + 1;elser = mid;}tails[l] = x;}return tails.size();}
};
// 检验二分边界
// tails[]: 1 3 5 -- x: 3/4
// tails[]: 1 3 5 7 -- x: 3/4/5🏠乘积最大子数组
152. 乘积最大子数组 - 力扣(LeetCode)
注意是“连续子数组”
AC 动规
1)滚动
本题,dp[i] 都是基于 dp[i -1] 得到的,所以可以将一维数组变成一个变量,即 “滚动数组”
2)坑
遍历数组,更新 3 个 dp 变量时,maxDp 基于上一个 maxDp 没问题
但是 maxDp 更新后,minDp 还是基于上一个 maxDp
所以需要一个临时变量保存上一个 maxDp
然后 dp 可以直接基于新的 maxDp
3)坑2
题目保证 32 位,也就是 10^9,但是,样例里有一组 10^19 次方的....
所以,有 4 个地方要加 double,防止类型不匹配 或 heap flow(堆溢出)
时间 O(n)
/*
滚动数组,一维数组变变量
maxDp[i] : 第 i 个元素结尾的最大值
minDp[i] : 第 i 个元素结尾的最小值
dp[i] : 只选前 i 的元素的最大值
*/
class Solution {
public:int maxProduct(vector<int>& nums) {int n = nums.size();if (n == 1)return nums[0];double maxDp = nums[0], minDp = nums[0], dp = nums[0];for (int i = 1; i < n; ++i) {double t = maxDp; // 临时变量maxDp = max(max((double)nums[i], maxDp*nums[i]), minDp*nums[i]);minDp = min(min((double)nums[i], t*nums[i]), minDp*nums[i]);dp = max(dp, maxDp); // 上一个 dp 和 新的 maxDp 取较大值}return (double)dp;}
};AC 用 0 分割
用 0 分割成多个连续的子数组,对每个子数组:
1)偶数个负数,直接相乘(负数数量 0, 2, 4, 6...)
2)奇数个负数:
a. 左到右相乘,直到最后一个负数之前
b. 右到左,直到最后一个负数之前
取 a. b. 的 max()
3)实际遍历中,先左到右遍历,后右到左遍历,单次遍历中,只需要动态更新最大值(包含了偶数,奇数个负数的两种情况)
时间 O(n)
class Solution {
public:int maxProduct(vector<int>& nums) {double ans = nums[0];double t = 1; // 临时变量保存乘积// 左到右for (int i = 0; i < nums.size(); ++i) {t *= nums[i];ans = max(ans, t);if (t == 0)t = 1; // 用 0 分割子数组}// 右到左t = 1;for (int i = nums.size() - 1; i >= 0; --i) {t *= nums[i];ans = max(ans, t);if (t == 0)t = 1;}return (int)ans;}
};🐬分割等和子集
416. 分割等和子集 - 力扣(LeetCode)
AC 二维DP
01背包画表格类似这样
坑:
和为奇数,直接返回 false,否则打表会发现,出现了一些奇怪的错误
含义:
dp[i][j] : 只从 [0, i] 区间里选,每个数最多选 1 次,和为 j
递推式:
选第 i 个:dp[i - 1][j - nums[i]]
不选第 i 个:dp[i - 1][j]
第 i 个数 == 总和的一半
dp[i][j] = dp[i - 1][j - nums[i]] || dp[i - 1][j] || (nums[i] == sum/2)
初始化:
根据递推式,只需初始化第 0 行,即只从 [0, 0] 区间选,和为 nums[0] 的 == 1,其他为 0
输出:
dp[n - 1][sum / 2]:表示从 [0, n - 1] 选, 和为总和一半, 即等和子集
O(n * sum/2)
// dp[i][j] = dp[i - 1][j - nums[i]] || dp[i - 1][j] || (nums[i] == sum/2)
// 输出 dp[n - 1][sum / 2]
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0, n = nums.size();for (auto x : nums)sum += x;if (sum % 2 == 1)return false; // 和为奇数// n 行, 每一行就是 vector<int>(), 这一行表示总和 0 ~ sum/2, 初始化为 0vector<vector<int>> dp(n, vector<int>(sum / 2 + 1, 0));if (nums[0] <= sum/2)dp[0][nums[0]] = 1; // 从 [0, 0] 选, 和为nums[0]for (int i = 1; i < n; ++i)for (int j = 0; j <= sum/2; ++j) {dp[i][j] = dp[i - 1][j] || (nums[i] == sum/2);if (j >= nums[i]) // 防止越界dp[i][j] = dp[i][j] || dp[i - 1][j - nums[i]];}return dp[n - 1][sum / 2];}
};
AC 一维DP
考虑到递推式 dp[i][j] 都是来源于 dp[i - 1][...],可以将二维变成一维,优化空间👇
那么为什么要逆序遍历子集的和 j 呢,因为,dp[j] 都是基于上一行的,旧的(未被修改的) dp[j] 和 dp[j - nums[i]]
如果顺序遍历,dp[j - nums[i]] 会被多次修改,也就是取了多个元素,而题目规定只能取一个
顺序遍历适合完全背包,而不是 01 背包

// dp[j] :和为 j
// dp[j] = dp[j - nums[i]] || dp[j] || (nums[i] == sum/2)
// 输出 dp[sum / 2]
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0, n = nums.size();for (auto x : nums)sum += x;if (sum % 2 == 1)return false; // 和为奇数// 和的一半 +1 个元素vector<int> dp(sum / 2 + 1, 0);if (nums[0] <= sum/2)dp[nums[0]] = 1; // 从 [0, 0] 选, 和为nums[0]for (int i = 1; i < n; ++i)for (int j = sum/2; j >= 0; --j) {dp[j] = dp[j] || (nums[i] == sum/2);if (j >= nums[i]) // 防止越界dp[j] = dp[j] || dp[j - nums[i]];}return dp[sum / 2];}
};
⚾最长有效括号
32. 最长有效括号 - 力扣(LeetCode)
AC 栈 + 哨兵
求连续的最长有效括号
如果不连续,栈就会被清空最后一个元素,再插入新的下标,即更新了栈顶的元素
初始插入 -1(哨兵),防止先遇到右括号,栈为空就 pop 导致的栈溢出
时间 O(n)
class Solution {
public:int longestValidParentheses(string s) {int ans = 0;if (s.size() == 0) return 0;stack<int> st;st.push(-1); // 防止溢出, 为后面的连续准备for (int i = 0; i < s.size(); ++i) {if (s[i] == '(') // 左括号st.push(i); else { // 右括号st.pop();if (st.empty())st.push(i);else ans = max(ans, i - st.top()); // 连续的长度}}return ans;}
};相关文章:

力扣 hot100 -- 动态规划(下)
目录 💻最长递增子序列 AC 动态规划 AC 动态规划(贪心) 二分 🏠乘积最大子数组 AC 动规 AC 用 0 分割 🐬分割等和子集 AC 二维DP AC 一维DP ⚾最长有效括号 AC 栈 哨兵 💻最长递增子序列 300. 最长递增子序列…...
【计算机毕业设计】018基于weixin小程序实习记录
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

力扣之有序链表去重
删除链表中的重复元素,重复元素保留一个 p1 p2 1 -> 1 -> 2 -> 3 -> 3 -> null p1.val p2.val 那么删除 p2,注意 p1 此时保持不变 p1 p2 1 -> 2 -> 3 -> 3 -> null p1.val ! p2.val 那么 p1,p2 向后移动 p1 …...

Apache配置与应用(优化apache)
Apache配置解析(配置优化) Apache链接保持 KeepAlive:决定是否打开连接保持功能,后面接 OFF 表示关闭,接 ON 表示打开 KeepAliveTimeout:表示一次连接多次请求之间的最大间隔时间,即两次请求之间…...
怎么将3张照片合并成一张?这几种拼接方法很实用!
怎么将3张照片合并成一张?在我们丰富多彩的日常生活里,是否总爱捕捉那些稍纵即逝的美好瞬间,将它们定格为一张张珍贵的图片?然而,随着时间的推移,这些满载回忆的宝藏却可能逐渐演变成一项管理挑战ÿ…...
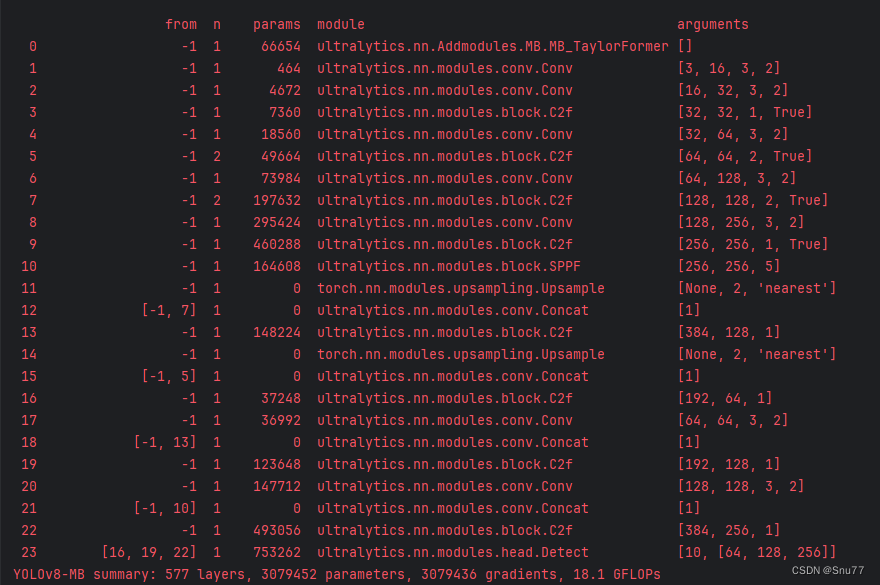
YOLOv10改进 | 图像去雾 | MB-TaylorFormer改善YOLOv10高分辨率和图像去雾检测(ICCV,全网独家首发)
一、本文介绍 本文给大家带来的改进机制是图像去雾MB-TaylorFormer,其发布于2023年的国际计算机视觉会议(ICCV)上,可以算是一遍比较权威的图像去雾网络, MB-TaylorFormer是一种为图像去雾设计的多分支高效Transformer…...
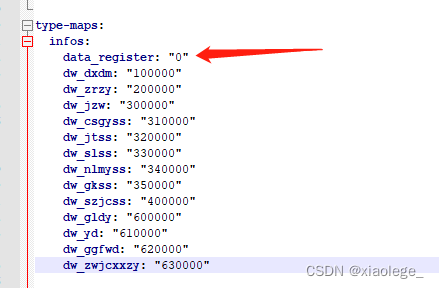
spring boot读取yml配置注意点记录
问题1:yml中配置的值加载到代码后值变了。 现场yml配置如下: type-maps:infos:data_register: 0ns_xzdy: 010000ns_zldy: 020000ns_yl: 030000ns_jzjz: 040000ns_ggglyggfwjz: 050000ns_syffyjz: 060000ns_gyjz: 070000ns_ccywljz: 080000ns_qtjz: 090…...

电子电气架构 --- 关于DoIP的一些闲思 下
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...

Java getSuperclass和getGenericSuperclass
1.官方API对这两个方法的介绍 getSuperclass : 返回表示此 Class 所表示的实体(类、接口、基本类型或 void)的超类的 Class。如果此 Class 表示 Object 类、一个接口、一个基本类型或 void,则返回 null。如果此对象表示一个数组类ÿ…...

ARM功耗管理标准接口之ACPI
安全之安全(security)博客目录导读 思考:功耗管理有哪些标准接口?ACPI&PSCI&SCMI? Advanced Configuration and Power Interface Power State Coordination Interface System Control and Management Interface ACPI可以被理解为一…...

2024年网络监控软件排名|10大网络监控软件是哪些
网络安全,小到关系到企业的生死存亡,大到关系到国家的生死存亡。 因此网络安全刻不容缓,在这里推荐网络监控软件。 2024年这10款软件火爆监控市场。 1.安企神软件: 7天免费试用https://work.weixin.qq.com/ca/cawcde06a33907e6…...

通过Arcgis从逐月平均气温数据中提取并计算年平均气温
通过Arcgis快速将逐月平均气温数据生成年平均气温数据。本次用2020年逐月平均气温数据操作说明。 一、准备工作 (1)准备Arcmap桌面软件; (2)准备2020年逐月平均气温数据(NC格式)、范围图层数据&…...

每日一题~abc356(对于一串连续数字 找规律,开数值桶算贡献)
添加链接描述 题意:对于给定的n,m 。计算0~n 每一个数和m & 之后,得到的数 的二进制中 1的个数的和。 一位一位的算。最多是60位。 我们只需要计算 在 1-n这些数上,有多少个数 第i位 为1. 因为是连续的自然数,每一位上1 的…...

商业合作方案撰写指南:让你的提案脱颖而出的秘诀
作为一名策划人,撰写一份商业合作方案需要细致的规划和清晰的表达。 它是一个综合性的过程,需要策划人具备市场洞察力、分析能力和创意思维。 以下是能够帮助你撰写一份有效的商业合作方案的关键步骤和要点: 明确合作目标:设定…...

【MySQL】锁(黑马课程)
【MySQL】锁 0. 锁的考察点1. 概述1. 锁的分类1.1 属性分类1.2 粒度分类 2. 全局锁2.1 全局锁操作2.2.1 备份问题 3. 表级锁3.1 表锁3.2 语法3.3 表共享读锁(读锁)3.4 表独占写锁(写锁)3.5 元数据锁(meta data lock, MDL)3.6 意向…...
1.10编程基础之简单排序--02:奇数单增序列
OpenJudge - 02:奇数单增序列http://noi.openjudge.cn/ch0110/02/ 描述 给定一个长度为N(不大于500)的正整数序列,请将其中的所有奇数取出,并按升序输出。 输入 共2行: 第1行为 N; 第2行为 N 个正整数,其间用空格间隔。 输出 增序输出的奇数序列,数据之间以逗号间隔。数…...

【leetcode78-81贪心算法、技巧96-100】
贪心算法【78-81】 121.买卖股票的最佳时机 class Solution:def maxProfit(self, prices: List[int]) -> int:dp[[0,0] for _ in range(len(prices))] #dp[i][0]第i天持有股票,dp[i][1]第i天不持有股票dp[0][0] -prices[0]for i in range(1, len(prices)):dp[…...

IEC62056标准体系简介-4.IEC62056-53 COSEM应用层
为在通信介质中传输COSEM对象模型,IEC62056参照OSI参考模型,制定了简化的三层通信模型,包括应用层、数据链路层(或中间协议层)和物理层,如图6所示。COSEM应用层完成对COSEM对象的属性和方法的访问ÿ…...

嵌入式应用开发之代码整洁之道
前言:本系列教程旨在如何将自己的代码写的整洁,同时也希望小伙伴们懂如何把代码写脏,以备不时之需,同时本系列参考 正点原子 , C代码整洁之道,编写可读的代码艺术。 #好的代码的特点 好的代码应该都有着几…...

iwconfig iwpriv学习之路
iwconfig和iwpriv是两个常用的wifi调试工具,最近需要使用这两个工具完成某款wifi芯片的定频测试,俗话说好记性不如烂笔头,于是再此记录下iwconfig和iwpriv的使用方式。 -----再牛逼的梦想,也抵不住傻逼般的坚持! ----2…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...

