链接服务器“XX”的OLEDB访问接口“MSOLEDBSQL”返回了消息“登录超时已过期” 解决方法
目录
- 1. 问题所示
- 2. 原理分析
- 3. 解决方法
1. 问题所示
出现如下问题：
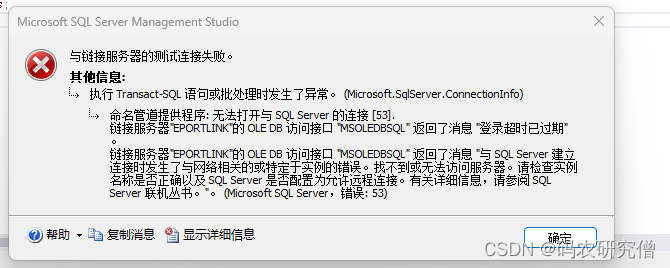
与链接服务器的测试连接失败。执行Transact-SQL 语句或批处理时发生了异常。命名管道提供程序：无法打开与SQL SERVER的链接[53]链接服务器“XX”的OLEDB访问接口“MSOLEDBSQL”返回了消息“登录超时已过期”链接服务器“XX”的OLEDB访问接口“MSOLEDBSQL”返回了消息与SQL Server建立连接时发生了与网络相关的或特定于实例的错误。找不到或无法访问服务器。请检查实例名称是否正确以及SQL Server是否配置为允许远程连接。有关信息，请参阅SQL SERVER联机丛书。
截图如下所示：
2. 原理分析
按照错误的Bug进行一个个排查
-
命名管道提供程序：无法打开与SQL SERVER的链接[53]
相关文章：
链接服务器“XX”的OLEDB访问接口“MSOLEDBSQL”返回了消息“登录超时已过期” 解决方法
目录 1. 问题所示2. 原理分析3. 解决方法1. 问题所示 出现如下问题： 与链接服务器的测试连接失败。执行Transact-SQL 语句或批处理时发生了异常。命名管道提供程序：无法打开与SQL SERVER的链接[53]链接服务器“XX”的OLEDB访问接口“MSOLEDBSQL”返回了消息“登录超时已过期…...
【AI伦理与社会责任】讨论人工智能在隐私保护、偏见消除、自动化对就业的影响等伦理和社会问题。
人工智能（AI）作为第四次产业革命的核心技术，在推动社会进步和经济发展的同时，也引发了一系列伦理和社会问题。以下从隐私保护、偏见消除以及自动化对就业的影响三个方面进行详细讨论。 一、隐私保护 人工智能技术的广泛应用涉及…...
Qt编程技巧小知识点（1）TCP缓存区数据读取
文章目录 Qt编程技巧小知识点（1）TCP缓存区数据读取小结 Qt编程技巧小知识点（1）TCP缓存区数据读取 TCP的socket对内存进行读取（使用socket->readall()）的时候输出的内容有时会进行局部倒置，其…...
vue 搭建 pinia
文章目录 环境设置存储读取数据【 storeToRefs】借助storeToRefs将store中的数据转为ref对象，方便在模板中使用【getters】当state中的数据，需要经过处理后再使用时，可以使用getters配置【$subscribe】通过 store 的 $subscribe() 方法侦听 s…...
什么是CLR
CLR，全称为Common Language Runtime，即公共语言运行时，是微软为.NET产品构建的运行环境，与Java的JVM（Java虚拟机）类似，可以看作是.NET的虚拟机。CLR的主要作用和特点如下： 主要作用…...
Spring MVC -01
Spring 的 MVC 框架 Spring的MVC框架是Spring框架的一部分，它提供了用于开发Web应用程序的一组组件和设计模式。MVC是Model-View-Controller的缩写，是一种设计模式，用于将应用程序的逻辑与用户界面分离。 在Spring的MVC框架中，Mo…...
山海鲸可视化——天地图画面和热力图
山海鲸引入天地图目前只有 iframe 的方式引入 首先我们创建一个文件夹 ——index.html ——index.js ——data.js 大家都是大佬，我就不详细介绍了，上代码都能看得懂 首先是index.html <!DOCTYPE html> <html lang"zh-CN"> <…...
Python 利用pandas处理CSV文件（DataFrame的基础用法）
前面介绍过通过Python标准库中的CSV模块处理CSV文件： Python 利用CSV模块处理数据 相比CSV模块，pandas的功能更加强大，本文将简单介绍如何通过pandas来处理CSV文件。 文章目录 一、pandas简介二、用法示例2.1 读取CSV文件2.1.1 read_csv参数…...
c++ 的（引用）和*（指针）
在C中，&（引用）和*（指针）在函数参数中的使用有各自的特点和用途。下面是它们的具体使用方式以及它们之间的一些区别： 引用（&） 使用方式: 引用作为函数参数时，可…...
人工智能算法工程师(中级)课程6-sklearn机器学习之聚类问题与代码详解
大家好，我是微学AI，今天给大家介绍一下人工智能算法工程师(中级)课程6-sklearn机器学习之聚类问题与代码详解。在机器学习领域，聚类是一种无监督学习方法，旨在将相似的数据点划分为同一类别。sklearn是一个广泛应用于机器学习的Py…...
Objective-C 中的 isa 不再是简单的结构体指针
了解 Objective-C 中的 isa 指针内存结构 在 Objective-C 中，isa 指针是对象和类之间的重要桥梁。它不仅帮助运行时系统识别对象的类型，还参与了一些内存和性能优化。本文将深入讲解 isa 指针的内存结构，包括其在早期和现代实现中的演变。 …...
中介子方程五十二
XXFXXaXnXaXXαXLXyXXWXuXeXKXXiXyXΣXXΣXXVXuXhXXWXηXXiXhXXpXiXXpXXbXXpXXiXpXXhXiXXηXWXXhXuXVXXΣXXΣXyXiXXKXeXuXWXXyXLXαXXaXnXaXXFXXaXnXaXXαXLXyXXWXuXeXKXXiXyXΣXXΣXXVXuXhXXWXηXXiXhXXpXiXXpXXbXXpXXiXpXXhXiXXηXWXXhXuXVXXΣXXΣXyXiXXKXeXuXWXXyXLXαXXa…...
LabVIEW在半导体自动化测试中的应用
半导体制造的复杂性和精密度要求极高，每一个生产步骤都需要严格的控制和监测。自动化测试设备在半导体制造中起到了关键作用，通过精密测量和数据分析，确保产品质量和生产效率。本文介绍如何使用LabVIEW结合研华硬件，开发一个用于半…...
政安晨：【Keras机器学习示例演绎】（五十三）—— 使用 TensorFlow 决策森林进行分类
目录 简介 设置 准备数据 定义数据集元数据 配置超参数 实施培训和评估程序 实验 1：使用原始特征的决策森林 检查模型 实验 2：目标编码决策森林 创建模型输入 使用目标编码实现特征编码 使用预处理器创建梯度提升树模型 训练和评估模型 实验…...
51单片机：电脑通过串口控制LED亮灭(附溢出率和波特率详解)
一、功能实现 1.电脑通过串口发送数据：0F 2.点亮4个LED 二、注意事项 1.发送和接受数据的文本模式 2.串口要对应 3.注意串口的波特率要和程序中的波特率保持一致 4.有无校验位和停止位 三、如何使用串口波特率计算器 1.以本程序为例 2.生成代码如下 void Uar…...
Java中的消息中间件选择与比较
Java中的消息中间件选择与比较 大家好，我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编，也是冬天不穿秋裤，天冷也要风度的程序猿！ 在分布式系统中，消息中间件是一种关键组件，它能帮助不同…...
react基础语法，模板语法，ui渲染，jsx，useState状态管理
创建一个react应用 这里使用create-react-app的脚手架构建项目（结构简洁，基于webpack-cli）， npx create-react-app [项目名称] 使用其他脚手架构建项目可以参考：react框架，使用vite和nextjs构建react项目…...
OJ-0710
示例1 input 4 100 200 300 5001 21 32 4output700100 200 500 300 示例2 input 4 100 200 300 500 1 2 1 3 1 4output1100100 200500300 示例3 input 6 100 200 300 400 300 550 1 2 1 3 1 4 2 5 2 6output1050100 200 300600 300400 import java.util.ArrayList; im…...
人工智能在自动驾驶中的目标检测研究
摘要 随着自动驾驶技术的快速发展，视觉识别作为核心技术之一，扮演着至关重要的角色。本文旨在探讨人工智能如何通过视觉识别在自动驾驶中进行目标检测。我们将详细讨论目标检测的基本原理、常用算法、最新进展、已有的开源项目及其在自动驾驶中的应用和…...
【合并两个有序数组】
合并两个有序数组 一、题目二、普通解法三、双指针 一、题目 二、普通解法 先合并后排序 补充:js合并数组方法详见https://blog.csdn.net/ACCPluzhiqi/article/details/131702269?fromshareblogdetail js排序方法见http://t.csdnimg.cn/wVCOP 时间复杂度：O(mn)…...
多云管理“拦路虎”：深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言：多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时，基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套：跨云网络构建数据…...
Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明：server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...
Swift 协议扩展精进之路：解决 CoreData 托管实体子类的类型不匹配问题（下）
概述 在 Swift 开发语言中，各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过，在涉及到多个子类派生于基类进行多态模拟的场景下，…...
生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端（Windows 使用 Git Bash，Mac/Linux 使用 Terminal）执行命令： ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明： -t rsa&#x…...
C# SqlSugar：依赖注入与仓储模式实践
C# SqlSugar：依赖注入与仓储模式实践 在 C# 的应用开发中，数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护，许多开发者会选择成熟的 ORM（对象关系映射）框架，SqlSugar 就是其中备受…...
免费数学几何作图web平台
光锐软件免费数学工具，maths,数学制图，数学作图，几何作图，几何，AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
CVPR2025重磅突破：AnomalyAny框架实现单样本生成逼真异常数据，破解视觉检测瓶颈！
本文介绍了一种名为AnomalyAny的创新框架，该方法利用Stable Diffusion的强大生成能力，仅需单个正常样本和文本描述，即可生成逼真且多样化的异常样本，有效解决了视觉异常检测中异常样本稀缺的难题，为工业质检、医疗影像…...
企业大模型服务合规指南：深度解析备案与登记制度
伴随AI技术的爆炸式发展，尤其是大模型（LLM）在各行各业的深度应用和整合，企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者，还是积极拥抱AI转型的传统企业，在面向公众…...
Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中，如何展示好看的实验结果图像非常重要！！！ 1、灰度原始图像 灰度图像每个像素点只有一个数值，代表该点的亮度（或…...
多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式，给定一个隐函数关系： F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标： 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...