蓝桥杯刷题冲刺 | 倒计时26天
作者:指针不指南吗
专栏:蓝桥杯倒计时冲刺🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾
文章目录
- 1.路径
- 2.特别数的和
- 3.MP3储存
- 4.求和
1.路径
-
题目
链接: 路径 - 蓝桥云课 (lanqiao.cn)
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝学习了最短路径之后特别高兴,他定义了一个特别的图,希望找到图 中的最短路径。
小蓝的图由 2021 个结点组成,依次编号 1 至 2021。
对于两个不同的结点 a, b,如果 a 和 b 的差的绝对值大于 21,则两个结点 之间没有边相连;如果 a 和 b 的差的绝对值小于等于 21,则两个点之间有一条 长度为 a 和 b 的最小公倍数的无向边相连。
例如:结点 1 和结点 23 之间没有边相连;结点 3 和结点 24 之间有一条无 向边,长度为 24;结点 15 和结点 25 之间有一条无向边,长度为 75。
请计算,结点 1 和结点 2021 之间的最短路径长度是多少。
提示:建议使用计算机编程解决问题。
-
第一次
#include<bits/stdc++.h> using namespace std;const int N=2030;int g[N][N];int gcd(int a,int b) {return b?gcd(b,a%b):a; }int gcs(int a,int b) {return a*b/gcd(a,b); }int main() {for(int i=1;i<2019;i++)for(int j=i+1;j<=2019;j++){if(j-i>21) g[i][j]=-1;else g[i][j]=gcs(i,j);}// 只会一个存储,emmm ,这个周末补上 图论 算法return 0; } -
正确题解
#include<iostream> #include<cstring> //memset()原型 using namespace std; const int N=3000; const int INF=0x3f; //这里可以理解为无穷大 int graph[N][N]; //邻接矩阵存储图 int dist[N]; //记录最短路径值 bool visited[N]; //判断节点是否访问int gcd(int a,int b){ //最大公约数 return b==0?a:gcd(b,a%b); } int lem(int a,int b){ //最小公倍数 return a*b/gcd(a,b); }int dijkstra(int n){//初始化 memset(dist,INF,sizeof(dist));memset(visited,false,sizeof(visited));dist[1]=0;for(int i=1;i<=n;++i){int k=-1;for(int j=1;j<=n;++j){ //获取距离源点最近点 if(!visited[j]&&(k==-1||dist[j]<dist[k])){k=j;}}visited[k]=true;for(int j=1;j<=n;++j){if(dist[k]+graph[k][j]<dist[j]){dist[j]=dist[k]+graph[k][j]; }}}if(dist[n]==INF) return -1;return dist[n]; } int main(){int n=2021; //节点数 //初始化 memset(graph,INF,sizeof(graph));//构图 for(int i=1;i<=n;++i){for(int j=1;j<=n;++j){if(abs(i-j)<=21){graph[i][j]=lem(i,j);}}}//求出最短路径,输出结果 cout<<dijkstra(n)<<endl;return 0; } -
反思
掌握了 新的方法来求解 最大公约数
到后面 ,看题解,有点看不懂了,没有学 图论 ,真是走不动路啊
2.特别数的和
-
题目
链接: 特别数的和 - 蓝桥云课 (lanqiao.cn)
小明对数位中含有 2、0、1、9 的数字很感兴趣(不包括前导 0),在 1 到 40 中这样的数包括 1、2、9、10 至 32、39 和 40,共 28 个,他们的和是 574。
请问,在 1 到 n 中,所有这样的数的和是多少?
输入描述
输入一行包含一个整数n(1≤n≤ 10410^4104)。
输出描述
输出一行,包含一个整数,表示满足条件的数的和。
示例
输入
40输出
574 -
我的题解
#include<bits/stdc++.h> using namespace std;int check(int x) {int t=x;while(t>0){int k=t%10;if(k==2||k==0||k==1||k==9)return x;t/=10;}return 0; }int main() {int n;cin>>n;int sum=0;for(int i=1;i<=n;i++){sum+=check(i);}cout<<sum;return 0; } -
反思
希望在 蓝桥杯 可以遇到 这么简单的题 qwq
3.MP3储存
-
题目
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
如果一个 MP3 文件占用磁盘的大小是 4MB,小蓝的硬盘还剩下 100GB 的空间,请问他还可以放多少个这样的 MP3 文件?
-
我的题解
#include<bits/stdc++.h> using namespace std;int main() {cout<<1024*100/4;return 0; } -
知识补充
1B(Byte 字节)=8bit,
1KB (Kilobyte 千字节)=1024B,
1MB (Megabyte 兆字节 简称“兆”)=1024KB,
1GB (Gigabyte 吉字节 又称“千兆”)=1024MB,
1TB (Trillionbyte 万亿字节 太字节)=1024GB,其中1024=2^10 ( 2 的10次方) -
反思
补充一下很基础的计算机知识,有点陌生了
4.求和
-
题目
链接: 求和 - 蓝桥云课 (lanqiao.cn)
给定 n 个整数 a*1,a2,⋅⋅⋅,*a n ,求它们两两相乘再相加的和,即:
S=a1⋅a2+a1⋅a3+⋯+a n−2⋅a n−1++ a n−1⋅a n
输入格式
输入的第一行包含一个整数 n。
第二行包含 n 个整数 a*1,a2,⋯,*a n。
输出格式
输出一个整数 S*,表示所求的和。请使用合适的数据类型进行运算。
样例输入
4 1 3 6 9样例输出
117 -
第一次
#include<bits/stdc++.h> using namespace std;typedef long long LL;const int N=2*1e6+10;int a[N];int main() {LL sum=0;int n;scanf("%d",&n);for(int i=0;i<n;i++)scanf("%d",&a[i]);for(int i=0;i<n-1;i++)for(int j=i+1;j<n;j++)sum+=a[i]*a[j];cout<<sum;return 0; }简单暴力,只能过 60%
-
第二次,优化
#include<bits/stdc++.h> using namespace std;typedef long long LL;const int N=2*1e6+10;int a[N];int main() {LL sum=0,ans=0;int n;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);sum+=a[i];}for(int i=0;i<n;i++){sum-=a[i]; //“a[1]*a[2]"到"a[n]*(a[n-1]+a[n-2]+....+a[1])"求和ans+=a[i]*sum; //在这里优化:运用乘法分配律}cout<<ans;return 0; } -
反思
学会 连乘的优化

相关文章:

蓝桥杯刷题冲刺 | 倒计时26天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.路径2.特别数的和3.MP3储存4.求和1.路径 题目 链接: 路径 - 蓝桥云课 (lanqiao.cn…...

嵌入式软件开发之Linux 用户权限管理
目录 Ubuntu 用户系统 权限管理 权限管理命令 权限修改命令 chmod 文件归属者修改命令 chown Ubuntu 用户系统 Ubuntu 是一个多用户系统,我们可以给不同的使用者创建不同的用户账号,每个用户使用各自的账号登陆,使用用户账号的目的一是方便…...

2023-03-15 RabbitMQ
RabbitMQ整合 官网erlang版本 : 20.3.8.x 官方rabbitMq版本: rabbitmq-server-generic-unix-3.7.14.tar.xz 1.安装 1.1 安装erlang 1.安装环境 yum -y install make gcc gcc-c kernel-devel m4 ncurses-devel openssl-devel2.在/usr/local/下创建erlangapp文件…...
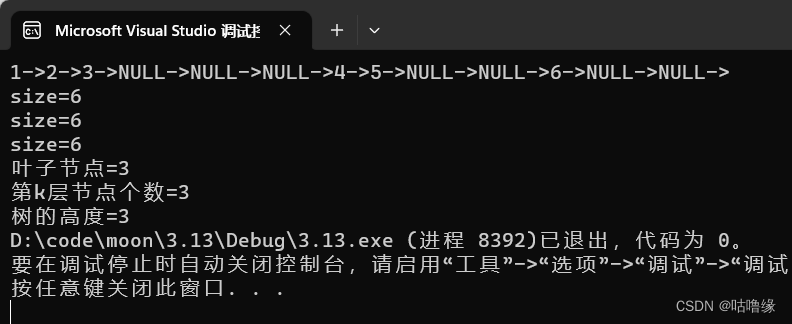
二叉树链式结构的实现
文章目录1.二叉树的遍历1.1前序、中序以及后序遍历1.2代码测试1.3层序遍历1.4二叉树遍历习题2.节点个数以及高度2.1二叉树节点个数2.2叶子节点个树2.3第k层节点个数2.4树的高度1.二叉树的遍历 1.1前序、中序以及后序遍历 学习二叉树结构,最简单的方式就是遍历。所…...

蓝桥杯刷题冲刺 | 倒计时28天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.卡片2.数字三角形3.购物单4.回文日期1.卡片 题目 链接: 卡片 - 蓝桥云课 (lanqiao…...

一文带你吃透操作系统
文章目录1. 进程、线程管理2. 内存管理3. 进程调度算法4. 磁盘调度算法5. 页面置换算法6. 网络系统7. 锁8. 操作系统知识点文章字数大约1.9万字,阅读大概需要65分钟,建议收藏后慢慢阅读!!!1. 进程、线程管理 进程和线程…...

计算机网络英文简称汇总
分类名词全拼汉译概述B2CBusiness-to-Consumer商对客概述P2PPeer-to-Peer对等概述C/SClient-Server服务器-客户机概述ITUInternational Telecommunication Union国际电信联盟概述IEEEInstitute of Electrical and Electronics Engineers电气与电子工程师协会概述ICCCInternatio…...
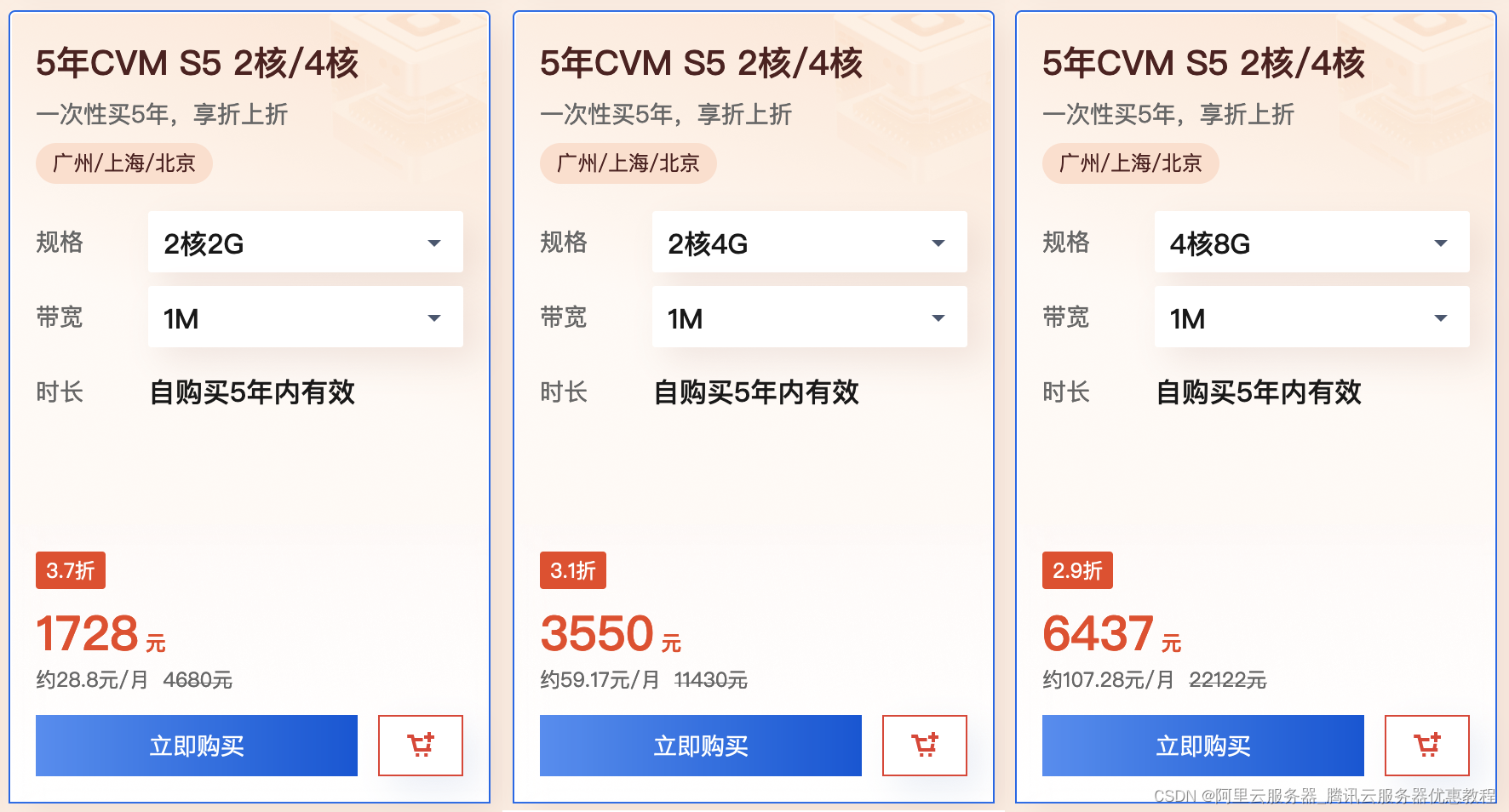
腾讯云云服务器标准型S5性能配置简单测评
腾讯云服务器标准型S5实例CPU采用Intel Xeon Cascade Lake或者Intel Xeon Cooper Lake处理器,主频2.5GHz,睿频3.1GHz,标准型S5云服务器基于全新优化虚拟化平台,配有全新的Intel Advanced Vector Extension (AVX-512) 指令集&#…...

RK3568平台开发系列讲解(Linux系统篇)消息队列
🚀返回专栏总目录 文章目录 一、创建消息队列二、发送和接收消息三、内核结构沉淀、分享、成长,让自己和他人都能有所收获!😄 📢消息队列在如下两个方面上比管道有所增强: 消息队列中的数据是有边界的,发送端和接收端能以消息为单位进行交流,而不再是无分隔的字节流…...

2021电赛国一智能送药小车(F题)设计报告
2021电赛国一智能送药小车(F题)设计报告 【写在前面的话】 电赛是一个很奇妙的过程,可能有些人觉得电赛的门槛太高,那便意味着,当你决定要参加电赛的那一刻起,这一段路、这些日子就注定不会太轻松…...

刚工作3天就被裁了....
前言 还有谁?刚上三天班就被公司公司的工作不适合我,叫我先提升一下。 后面我也向公司那边讨要了一个说法,我只能说他们那边的说辞让我有些不服气。 现在之所以把这件事上记录一下,一是记录一下自己的成长轨迹,二是…...
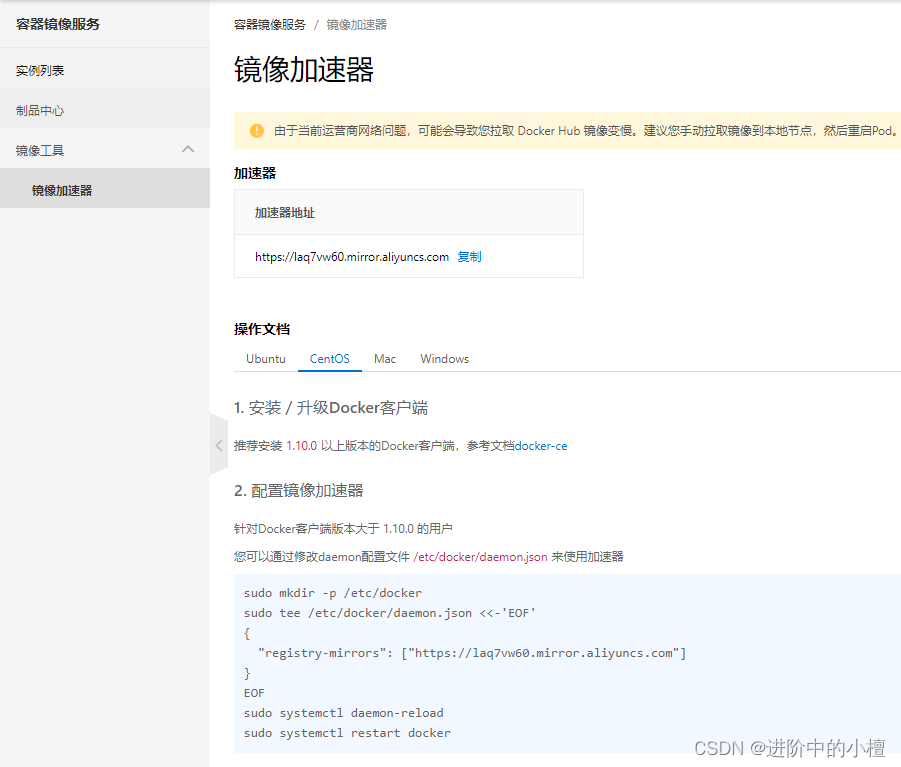
docker安装elasticsearch与head教程完整版—.NET Core Web Api与elasticsearch打造全站全文搜索引擎
默认已经有docker环境 下载与安装 elasticsearch ,从hub.docker里面可以看到最新版本的镜像,选择你想要的版本 本教程是以 7.17.7 为案例,为啥不适用最新的,首先个人一般需用最新的版本,如果有亢很难填,其次…...

蓝桥冲刺31天之315
没有一个冬天不可逾越 也没有一个春天不会来临 所有美好的食物,都会有一个等待的过程 低谷时蛰伏,静默时沉淀 做三四月的事,在八九月自有答案 目录 A:0的个数 题目描述: 输入格式 输出格式 样例输入 样例输出 评测用例规模与…...
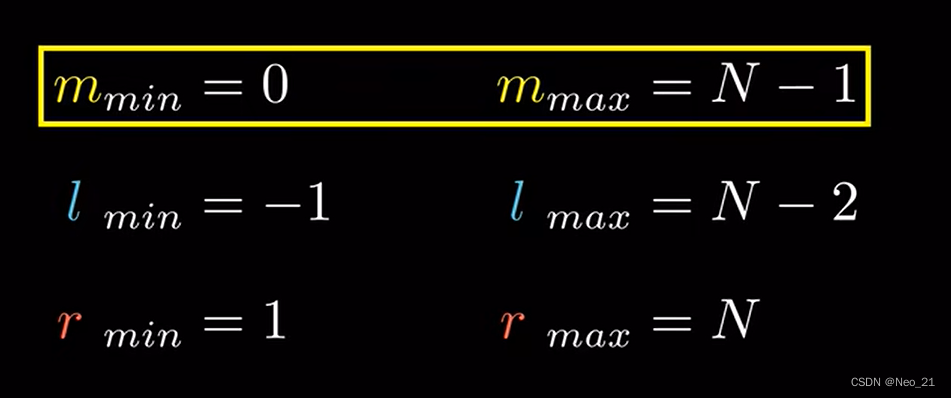
常见排序算法
/懂了和写出来是两码事啊啊......orz./ Talk is cheap, show me the code 一、快速排序 直接背模板就能过: 当xq[lr>>1]的边界情况 此时x取的是序列中间靠左的位置(如果序列个数为奇,则取正中间,如果为偶,则取中间靠左),此时如果元素个数为2, 则中间靠左就…...
C语言实现学生成绩管理系统思考
学生成绩管理系统思考 作业要求: 目录 思路 基本函数 学习理解大佬的代码: 完成作业: 思路 学生成绩管理系统,首先要初始化系统, 用C语言做学生实验管理系统要求实现对某班学生3门课程(包括语文、数…...
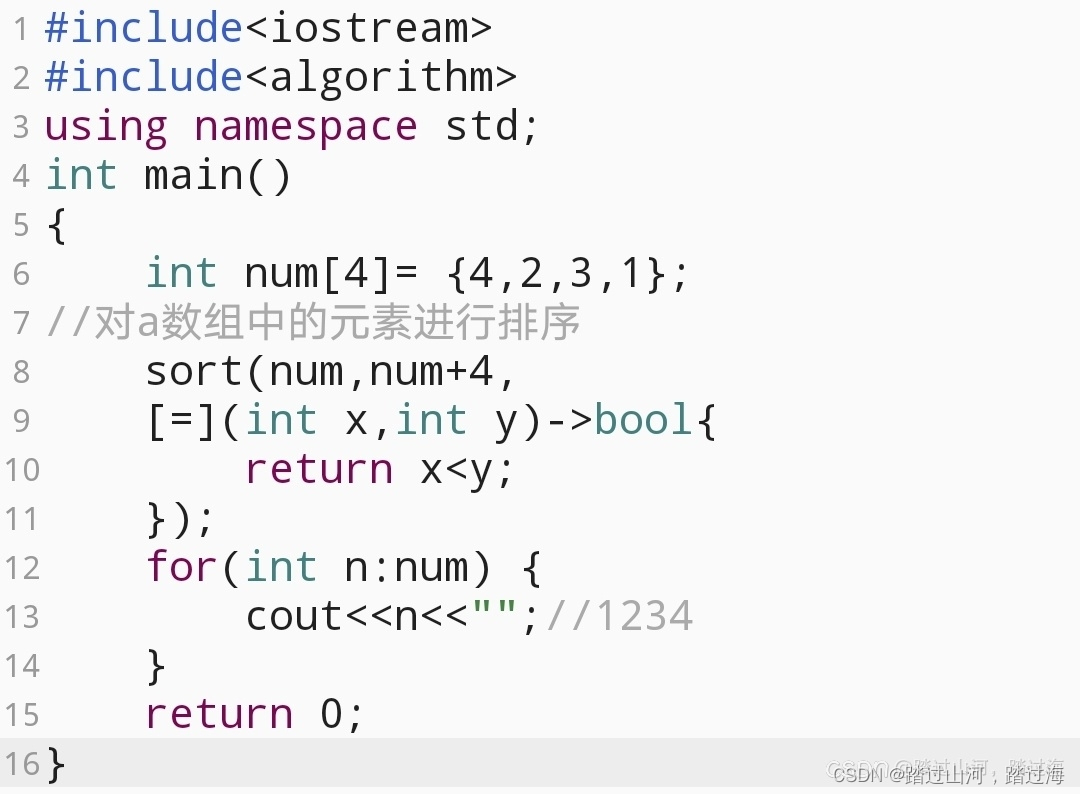
C++11中Lambda新特性
1.定义 lambda匿名函数的语法格式: [外部变量访问方式说明符](参数)mutablenoexcept/throw()->返回值类型 {函数体; };其中各部分的含义分别为: a.[外部变量方位方式说明符] []方括号用于向编译器表明当前是一个lambda表达式,其不能被省略…...
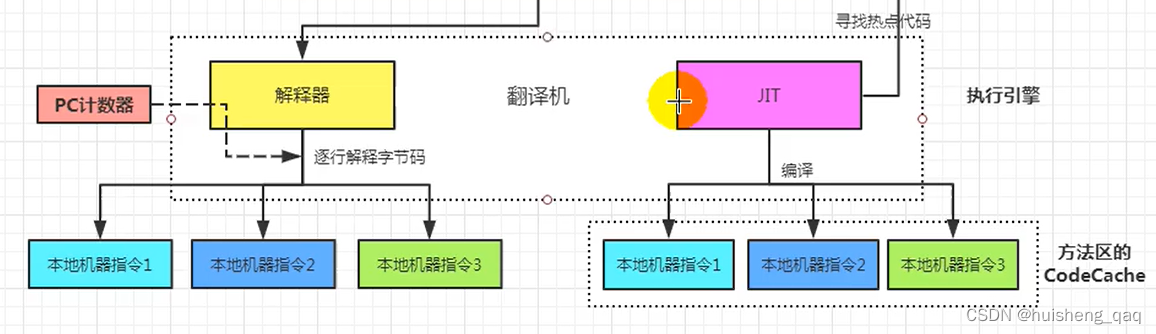
【jvm系列-01】初识虚拟机与java虚拟机
初识虚拟机与java虚拟机一,虚拟机与java虚拟机1,虚拟机2,java虚拟机3,jvm整体结构图4,jvm的架构模型5,jvm的生命周期6,jvm的种类划分6.1,Sun Classic Vm6.2,Exact VM6.3&…...

「Python 基础」数据库应用编程
Python 定义了一套 DB-API,任何数据库要连接到 Python,只需要提供符合 Python 标准的数据库驱动即可; 文章目录1. 连接 SQLite1. 建表、插入数据2. 查询数据2. 连接 MySQL1. 安装驱动2. 演示连接3. SQLAlchemy1. 安装2. DBSession3. add4. qu…...
一个nginx的小项目,不写代码,实现在局域网内访问其他电脑的网页
准备工作 下载nginx //官网 https://nginx.org/en/download.html //直接下载 https://nginx.org/download/nginx-1.23.3.zip解压 下载一个html项目,或者自己随便写一个 我是直接下载的,然后使用的是第一个01 https://gitee.com/StarPort/HTML_CSSTe…...

23.3.14打卡 2022年江西省大学生程序设计竞赛(正式赛)ABL
就写了签到, 其他题没写, 这场好像3题就银了 纪念一下3.14原粥率日 比赛链接:https://ac.nowcoder.com/acm/contest/43898 A题 Special Adjustment Method 题意 给出非负整数x, y, z 你可以让其中两个数字-1, 另外一个2, 使得x2y2z2x^2y^{2}z^{2}x2y2z2最大 题解 这题很容…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
