08.C2W3.Auto-complete and Language Models
往期文章请点这里
目录
- N-Grams: Overview
- N-grams and Probabilities
- N-grams
- Sequence notation
- Unigram probability
- Bigram probability
- Trigram Probability
- N -gram probability
- Quiz
- Sequence Probabilities
- Probability of a sequence
- Sequence probability shortcomings
- Approximation by N gram probabilities
- Quiz
- Starting and Ending Sentences
- Start of sentence token \<s\>
- End of sentence token \</s\> -motivation
- End of sentence token \</s\> -solution
- Example-bigram
- Quiz
- The N-gram Language Model
- Count matrix
- Probability matrix
- Language model
- Log probability
- Generative Language model
- Language Model Evaluation
- Test data
- Perplexity
- Perplexity for bigram models
- Log perplexity
- Example
- Out of Vocabulary Words
- Out of vocabulary words
- Using \<UNK\> in corpus
- How to create vocabulary V
- Quiz
- Smoothing
- Missing N-grams in training corpus
- Smoothing
- Backoff
- Interpolation
- Quiz
往期文章请点这里
N-Grams: Overview
● Create language model (LM) from text corpus to
○ Estimate probability of word sequences
○ Estimate probability of a word following a sequence of words
● Apply this concept to autocomplete a sentence with most likely suggestions

语言模型在自然语言处理(NLP)和人工智能领域有着广泛的应用,以下是它们在特定领域中的应用:
语音识别(Speech Recognition):
语音识别系统将人类的语音转换成书面文本。语言模型在这个过程中起到关键作用,因为它们帮助系统理解语音片段中单词的上下文和语法结构。通过语言模型,系统能够更准确地预测一个单词序列的可能性,从而提高语音到文本转换的准确性。

拼写检查与纠正(Spelling Correction):
语言模型可以用来检测和纠正文本中的拼写错误。由于语言模型知道哪些单词序列在特定语言中是常见的或符合语法规则的,它们可以识别出不符合这些规则的单词,提示或自动更正为正确的拼写。例如,如果用户错误地输入了“recieve”,语言模型可以识别出这不是一个常见单词,并建议更正为“receive”。

辅助交流(Augmentative and Alternative Communication, AAC):
辅助交流设备或系统帮助那些有语言障碍或沟通困难的人表达自己。语言模型可以集成到这些系统中,提供个性化的预测和建议,帮助用户更快地构建句子和表达思想。例如,对于使用特殊设备进行交流的用户,语言模型可以预测他们可能想要表达的下一个单词或短语,从而提高交流效率。

主要目标:
●Process text corpus to N-gram language model
●Out of vocabulary words
●Smoothing for previously unseen N-grams
●Language model evaluation
N-grams and Probabilities
N-grams
N-gram 是自然语言处理中用于描述文本数据的一种统计模型。简单来说,一个 N-gram 是由 N 个连续的词(words)组成的序列。在这个序列中,每个词被称作一个“gram”,并且这个序列可以被用来捕捉文本中的局部上下文信息。
以下是不同 N 值的 N-gram 的一些例子:
对于 Unigram(1-gram):N=1,它只包含一个词。例如,“cat”就是一个 unigram。
对于 Bigram(2-gram):N=2,它包含两个连续的词。例如,“cat sat”就是一个 bigram。
对于 Trigram(3-gram):N=3,它包含三个连续的词。例如,“cat sat on”就是一个 trigram。
N-gram 模型在语言模型中非常重要,因为它们可以用来预测文本序列中下一个词出现的概率。例如,在一个 bigram 模型中,给定第一个词,模型可以预测第二个词出现的概率。这种模型对于诸如拼写检查、语法分析、机器翻译和语音识别等应用至关重要。
然而,N-gram 模型也存在一些局限性,比如当 N 值较大时,模型可能会遇到数据稀疏问题,因为大量的词序列在训练数据中可能只出现很少的次数或从未出现过。此外,N-gram 模型通常忽略了词序之外的上下文信息,如句法和语义。
理解 N-gram 的关键是认识到它们提供了一种简单但有效的方式来捕捉和表示文本数据中的局部依赖关系。
另外一个例子:
Corpus: I am happy because I am learning
Unigrams: {I , am, happy, because, learning}
Bigrams: {I am, am happy , happy because …}这里I happy不是Bigrams,必须要连续的两个词;I am在语料库中出现两次,只会记录一次
Trigrams: {I am happy , am happy because , …}
Sequence notation
假设现有语料库中有500个单词:

则单词序列可以表示为:
w 1 m = w 1 w 2 ⋯ w m w_1^m=w_1w_2\cdots w_m w1m=w1w2⋯wm
例如第一个到第三个单词的序列:
w 1 3 = w 1 w 2 w 3 w_1^3=w_1w_2w_3 w13=w1w2w3
语料库中最后三个词可以表示为:
w m − 2 m = w m − 2 w m − 1 w m w_{m-2}^m=w_{m-2}w_{m-1}w_m wm−2m=wm−2wm−1wm
Unigram probability
假设语料库为:I am happy because I am learning
语料库大小 m = 7 m=7 m=7
对于单词I: P ( I ) = 2 7 P(I)=\cfrac{2}{7} P(I)=72
对于单词happy: P ( h a p p y ) = 1 7 P(happy)=\cfrac{1}{7} P(happy)=71
Unigram probability公式为:
P ( w ) = C ( w ) m P(w)=\cfrac{C(w)}{m} P(w)=mC(w)
Bigram probability
假设语料库为:I am happy because I am learning
则前一个单词是I,后一个单词是am的概率为: P ( a m ∣ I ) = C ( I a m ) C ( I ) = 2 2 = 1 P(am|I)=\cfrac{C(I\space am)}{C(I)}=\cfrac{2}{2}=1 P(am∣I)=C(I)C(I am)=22=1
前一个单词是I,后一个单词是happy的概率为: P ( h a p p y ∣ I ) = C ( I h a p p y ) C ( I ) = 0 2 = 0 P(happy|I)=\cfrac{C(I\space happy)}{C(I)}=\cfrac{0}{2}=0 P(happy∣I)=C(I)C(I happy)=20=0
前一个单词是am,后一个单词是learning的概率为: P ( l e a r n i n g ∣ a m ) = C ( a m l e a r n i n g ) C ( a m ) = 1 2 P(learning|am)=\cfrac{C(am\space learning)}{C(am)}=\cfrac{1}{2} P(learning∣am)=C(am)C(am learning)=21
Bigram probability公式为:
P ( y ∣ x ) = C ( x y ) ∑ w C ( x w ) = C ( x y ) C ( x ) P(y|x)=\cfrac{C(x\space y)}{\sum_wC(x\space w)}=\cfrac{C(x\space y)}{C(x)} P(y∣x)=∑wC(x w)C(x y)=C(x)C(x y)
Trigram Probability
假设语料库为:I am happy because I am learning
前两个单词是I am,后一个单词是happy的概率为: P ( h a p p y ∣ I a m ) = C ( I a m h a p p y ) C ( I a m ) = 1 2 P(happy|I\space am)=\cfrac{C(I\space am\space happy)}{C(I\space am)}=\cfrac{1}{2} P(happy∣I am)=C(I am)C(I am happy)=21
Trigram Probability公式为:
P ( w 3 ∣ w 1 2 ) = C ( w 1 2 w 3 ) C ( w 1 2 ) P(w_3|w_1^2)=\cfrac{C(w_1^2w_3)}{C(w_1^2)} P(w3∣w12)=C(w12)C(w12w3)
N -gram probability
直接给公式:
P ( w N ∣ w 1 N − 1 ) = C ( w 1 N − 1 w N ) C ( w 1 N − 1 ) P(w_N|w_1^{N-1})=\cfrac{C(w_1^{N-1}w_N)}{C(w_1^{N-1})} P(wN∣w1N−1)=C(w1N−1)C(w1N−1wN)
分子: C ( w 1 N − 1 w N ) = C ( w 1 N ) C(w_1^{N-1}w_N)=C(w_1^{N}) C(w1N−1wN)=C(w1N)
Quiz
Corpus:
In every place of great resort the monster was the fashion. They sang of it in the cafes, ridiculed it in the papers, and rep res ented it on the stage. ” (Jules Verne, Twenty Thousand Leagues under the Sea)
In the context of our corpus, what is the probability of word “papers” following the phrase “it in the”.
Answer: 1/2
解析:it in the总共出现了2次,后面接papers出现了1次
Sequence Probabilities
Probability of a sequence
给定一个句子,其出现概率如何计算?
根据链式法则:
P ( A , B , C , D ) = P ( A ) P ( B ∣ A ) P ( C ∣ A , B ) P ( D ∣ A , B , C ) P(A, B,C, D)= P(A)P(B|A)P(C|A, B)P(D|A, B, C) P(A,B,C,D)=P(A)P(B∣A)P(C∣A,B)P(D∣A,B,C)
根据条件概率:
P ( B ∣ A ) = P ( A , B ) P ( A ) ⇒ P ( A , B ) = P ( A ) P ( B ∣ A ) P(B|A)=\cfrac{P(A,B)}{P(A)}\xRightarrow{} P(A,B)=P(A)P(B|A) P(B∣A)=P(A)P(A,B)P(A,B)=P(A)P(B∣A)
则某句话出现的概率为:
P(the teacher drinks tea)=P(the)P(teacher|the)P(drinks |the teacher)P(tea |the teacher drinks)
Sequence probability shortcomings
最大的问题:Corpus almost never contains the exact sentence we’re interested in or even its longer subsequences!
例如上面的例子中最后一项:
P ( t e a ∣ t h e t e a c h e r d r i n k s ) = C ( t h e t e a c h e r d r i n k s t e a ) C ( t h e t e a c h e r d r i n k s ) P(tea |the\space teacher\space drinks)=\cfrac{C(the\space teacher\space drinks\space tea)}{C(the\space teacher\space drinks)} P(tea∣the teacher drinks)=C(the teacher drinks)C(the teacher drinks tea)
可以预想到分子和分母项在语料中出现的次数估计为0,会使得P(the teacher drinks tea)计算依赖相乘的结果也为0
Approximation by N gram probabilities
为了避免上面提到的情况,将条件概率中的条件限制为前一个单词:
P ( t e a ∣ t h e t e a c h e r d r i n k s ) ≈ P ( t e a ∣ d r i n k s ) P(tea |the\space teacher\space drinks)\approx P(tea|drinks) P(tea∣the teacher drinks)≈P(tea∣drinks)
P ( t h e t e a c h e r d r i n k s t e a ) = P ( t h e ) P ( t e a c h e r ∣ t h e ) P ( d r i n k s ∣ t h e t e a c h e r ) P ( t e a ∣ t h e t e a c h e r d r i n k s ) ≈ P ( t h e ) P ( t e a c h e r ∣ t h e ) P ( d r i n k s ∣ t e a c h e r ) P ( t e a ∣ d r i n k s ) P(the\space teacher\space drinks\space tea)=P(the)P(teacher|the)P(drinks |the\space teacher)P(tea |the\space teacher\space drinks)\\ \approx P(the)P(teacher|the)P(drinks |teacher)P(tea |drinks) P(the teacher drinks tea)=P(the)P(teacher∣the)P(drinks∣the teacher)P(tea∣the teacher drinks)≈P(the)P(teacher∣the)P(drinks∣teacher)P(tea∣drinks)
当然,还可以根据Markov assumption: only last N words matter
Bigram某个单词出现概率:
P ( w n ∣ w 1 n − 1 ) ≈ P ( w n ∣ w n − 1 ) P(w_n | w_1^{n-1}) \approx P(w_n | w_{n-1}) P(wn∣w1n−1)≈P(wn∣wn−1)
N-gram某个单词出现概率:
P ( w n ∣ w 1 n − 1 ) ≈ P ( w n ∣ w n − N + 1 n − 1 ) P(w_n | w_1^{n-1}) \approx P(w_n|w_{n-N+1}^{n-1}) P(wn∣w1n−1)≈P(wn∣wn−N+1n−1)
Bigram整个句子出现概率:
P ( w 1 n ) ≈ P ( w 1 ) P ( w 2 ∣ w 1 ) ⋯ P ( w n ∣ w n − 1 ) P(w_1^n)\approx P(w_1)P(w_2|w_1)\cdots P(w_n|w_{n-1}) P(w1n)≈P(w1)P(w2∣w1)⋯P(wn∣wn−1)
Quiz
Given these conditional probabilities
P(Mary)=0.1;
P(likes)=0.2;
P(cats)=0.3
P(Mary|likes) =0.2;
P(likes|Mary) =0.3;
P(cats|likes)=0.1;
P(likes|cats)=0.4
Approximate the probability of the following sentence with bigrams: “Mary likes cats”
Answer:0.003
解析:P(Mary likes cats)=P(Mary)P(likes|Mary)P(cats|likes)=0.1×0.3×0.1=0.003
Starting and Ending Sentences
Start of sentence token <s>
P ( t h e t e a c h e r d r i n k s t e a ) ≈ P ( t h e ) P ( t e a c h e r ∣ t h e ) P ( d r i n k s ∣ t e a c h e r ) P ( t e a ∣ d r i n k s ) P(the\space teacher\space drinks\space tea) \approx P(the)P(teacher|the)P(drinks |teacher)P(tea |drinks) P(the teacher drinks tea)≈P(the)P(teacher∣the)P(drinks∣teacher)P(tea∣drinks)
可以看到第一个单词没有前置词,无法使用Bigram来计算条件概率,因此,我们通常会加上一个特殊项,使得上面的公式右边每一项都变成Bigram,the teacher drinks tea就变成了<s> the teacher drinks tea,概率计算变成:
P ( < s > t h e t e a c h e r d r i n k s t e a ) ≈ P ( t h e ∣ < s > ) P ( t e a c h e r ∣ t h e ) P ( d r i n k s ∣ t e a c h e r ) P ( t e a ∣ d r i n k s ) P(<s>\space the\space teacher\space drinks\space tea) \approx P(the|<s>)P(teacher|the)P(drinks |teacher)P(tea |drinks) P(<s> the teacher drinks tea)≈P(the∣<s>)P(teacher∣the)P(drinks∣teacher)P(tea∣drinks)
对于Trigram:
P ( t h e t e a c h e r d r i n k s t e a ) ≈ P ( t h e ) P ( t e a c h e r ∣ t h e ) P ( d r i n k s ∣ t h e t e a c h e r ) P ( t e a ∣ t e a c h e r d r i n k s ) P(the\space teacher\space drinks\space tea)\approx P(the)P(teacher|the)P(drinks| the\space teacher)P(tea|teacher\space drinks) P(the teacher drinks tea)≈P(the)P(teacher∣the)P(drinks∣the teacher)P(tea∣teacher drinks)
需要加上两个<s>,得到:<s> <s> the teacher drinks tea
进一步推广到N-gram,则需要添加N-1个<s>
End of sentence token </s> -motivation
第一个动机:
对于公式:
P ( y ∣ x ) = C ( x , y ) ∑ w C ( x , w ) = C ( x , y ) C ( x ) P(y|x)=\cfrac{C(x,y)}{\sum_wC(x,w)}=\cfrac{C(x,y)}{C(x)} P(y∣x)=∑wC(x,w)C(x,y)=C(x)C(x,y)
当我们计算最后一个词的时候,上面公式的分母不一定相等,即: ∑ w C ( x , w ) ≠ C ( x ) \sum_wC(x,w)\neq C(x) ∑wC(x,w)=C(x)
例如有语料库:
<s> Lyn drinks chocolate
<s> John drinks
数一下drinks后面带有单词出现的次数是1:
∑ w C ( d r i n k s , w ) = 1 \sum_wC(drinks,w)=1 ∑wC(drinks,w)=1
drinks单独出现的次数是2:
∑ w C ( d r i n k s ) = 2 \sum_wC(drinks)=2 ∑wC(drinks)=2
第二个动机:
假如有语料库:
<s> yes no
<s> yes yes
<s> no no
先生成长度为2的句子:
<s> yes yes
<s> yes no
<s> no no
<s> no yes
以第一个<s> yes yes为例,计算其出现概率:
P ( < s > y e s y e s ) = P ( y e s ∣ < s > ) × P ( y e s ∣ y e s ) = C ( < s > , y e s ) ∑ w C ( < s > , w ) × C ( y e s , y e s ) ∑ w C ( y e s , w ) = 2 3 × 1 2 = 1 3 P(<s>\space yes\space yes)=P(yes|<s>)\times P(yes|yes)\\ =\cfrac{C(<s>,yes)}{\sum_wC(<s>,w)}\times\cfrac{C(yes,yes)}{\sum_wC(yes,w)}\\ =\cfrac{2}{3}\times\cfrac{1}{2}=\cfrac{1}{3} P(<s> yes yes)=P(yes∣<s>)×P(yes∣yes)=∑wC(<s>,w)C(<s>,yes)×∑wC(yes,w)C(yes,yes)=32×21=31
同理,可以计算得到<s> yes no出现概率为:1/3;<s> no no出现概率为:1/3;<s> no yes 出现概率为:0;
也就是说所有长度为2的句子出现概率总和为: ∑ 2 w o r d P ( ⋯ ) = 1 / 3 + 1 / 3 + 1 / 3 + 0 = 1 \sum_{2\space word}P(\cdots)=1/3+1/3+1/3+0=1 ∑2 wordP(⋯)=1/3+1/3+1/3+0=1
同理可以计算长度为3的句子:

这个结果是不符合我们的假设的,正常来说,根据语料库生成所有句子的可能性加起来应该为1,而不是某个长度的句子生成概率为1:
∑ 2 w o r d P ( ⋯ ) + ∑ 3 w o r d P ( ⋯ ) + ⋯ = 1 \sum_{2\space word}P(\cdots)+\sum_{3\space word}P(\cdots)+\cdots=1 2 word∑P(⋯)+3 word∑P(⋯)+⋯=1
End of sentence token </s> -solution
解决方法就是在句末加</s>,例如:<s> the teacher drinks tea </s>,出现概率为:
P ( t h e ∣ < s > ) P ( t e a c h e r ∣ t h e ) P ( d r i n k s ∣ t e a c h e r ) P ( t e a ∣ d r i n k s ) P ( < / s > ∣ t e a ) P(the|<s>)P(teacher|the)P(drinks |teacher)P(tea |drinks)P(</s>|tea) P(the∣<s>)P(teacher∣the)P(drinks∣teacher)P(tea∣drinks)P(</s>∣tea)
注意:和句首不一样,即使是N-gram也只需要加一个</s>,例如Trigram:
the teacher drinks tea=> <s> <s> the teacher drinks tea </s>
对于动机1:
<s> Lyn drinks chocolate </s>
<s> John drinks </s>
数一下drinks后面带有单词出现的次数是2:
∑ w C ( d r i n k s , w ) = 2 \sum_wC(drinks,w)=2 ∑wC(drinks,w)=2
drinks单独出现的次数是2:
∑ w C ( d r i n k s ) = 2 \sum_wC(drinks)=2 ∑wC(drinks)=2
Example-bigram
假设语料库为:
<s> Lyn drinks chocolate </s>
<s> John drinks tea </s>
<s> Lyn eats chocolate </s>
以下是一些单词出现概率计算结果:
P ( J o h n ∣ < s > ) = 1 3 P ( < / s > ∣ t e a ) = 1 1 P(John|<s>)=\cfrac{1}{3}\quad P(</s>|tea)=\cfrac{1}{1} P(John∣<s>)=31P(</s>∣tea)=11
P ( c h o c o l a t e ∣ e a t s ) = 1 1 P ( L y n ∣ < s > ) = 2 3 P(chocolate |eats )=\cfrac{1}{1}\quad P(Lyn |<s>)=\cfrac{2}{3} P(chocolate∣eats)=11P(Lyn∣<s>)=32
对于第一句话出现概率为:
P ( s e n t e n c e ) = 2 3 × 1 2 × 1 2 × 2 2 = 1 6 P(sentence)=\cfrac{2}{3}\times\cfrac{1}{2}\times\cfrac{1}{2}\times\cfrac{2}{2}=\cfrac{1}{6} P(sentence)=32×21×21×22=61
可以看到,计算结果要比3个句子情况下出现概率为1/3的概率要低,剩余概率可以分布到语料库中使用bigram生成的其他句子中,这就是模型的泛化方式。
Quiz
Question:
Given these conditional probabilities
P(Mary)=0.1;
P(likes)=0.2;
P(cats)=0.3
P(Mary|<s>)=0.2;
P(</s>|cats)=0.6
P(likes|Mary) =0.3;
P(cats|likes)=0.1
Approximate the probability of the following sentence with bigrams: “<s> Mary likes cats </s>”
Answer: 0.0036
解析:P(Mary|<s>)P(likes|Mary)P(cats|likes)P(</s>|cats)=0.2×0.3×0.1×0.6
The N-gram Language Model
Count matrix
在N-gram的公式中:
P ( w n ∣ w n − N + 1 n − 1 ) = C ( w n − N + 1 n − 1 , w n ) C ( w n − N + 1 n − 1 ) P(w_n|w_{n-N+1}^{n-1})=\cfrac{C(w_{n-N+1}^{n-1},w_n)}{C(w_{n-N+1}^{n-1})} P(wn∣wn−N+1n−1)=C(wn−N+1n−1)C(wn−N+1n−1,wn)
分子: C ( w n − N + 1 n − 1 , w n ) C(w_{n-N+1}^{n-1},w_n) C(wn−N+1n−1,wn)
Count matrix计算了在语料库中出现的所有共现次数。
它的行值是非重复语料库前一词
列是所有非重复语料当前词
Bigram count matrix实例:
Corpus:<s> I study I learn </s>

上面的study I在语料库出现1次
Probability matrix
上面以及计算了分子,再计算出分母后就得到概率矩阵
Divide each cell by its row sum
s u m ( r o w ) = ∑ w ∈ V C ( w n − N + 1 n − 1 , w n ) = C ( w n − N + 1 n − 1 ) sum(row)=\sum_{w\in V}C(w_{n-N+1}^{n-1},w_n)=C(w_{n-N+1}^{n-1}) sum(row)=w∈V∑C(wn−N+1n−1,wn)=C(wn−N+1n−1)
根据Count matrix计算每行的求和

然后计算概率得到Probability matrix:

Language model
通过Probability matrix,Language model可以计算:
○ Sentence probability
○ Next word prediction
例如,根据上一节的Probability matrix,计算<s> I learn </s>这个句子的概率:
P ( s e n t e n c e ) = P ( I ∣ < s > ) P ( l e a r n ∣ I ) P ( < / s > ∣ l e a r n ) = 1 × 0.5 × 1 = 0.5 P(sentence)=P(I|<s>)P(learn|I)P(</s>|learn)=1\times0.5\times1=0.5 P(sentence)=P(I∣<s>)P(learn∣I)P(</s>∣learn)=1×0.5×1=0.5
Log probability
同样的,这里也出现了多个概率相乘的情况,需要使用对数计算防止下溢。
P ( w 1 n ) ≈ ∏ i = 1 n P ( w i ∣ w i − 1 ) P(w_1^n ) \approx\prod_{i=1}^{n} P(w_i | w_{i-1}) P(w1n)≈i=1∏nP(wi∣wi−1)
取对数后:
log ( P ( w 1 n ) ) ≈ ∑ i = 1 n log ( P ( w i ∣ w i − 1 ) ) \log(P(w_1^n ) )\approx\sum_{i=1}^{n}\log( P(w_i | w_{i-1})) log(P(w1n))≈i=1∑nlog(P(wi∣wi−1))
Generative Language model
实例:

可以看到,生成语言模型算法大概步骤如下:
- Choose sentence start
- Choose next bigram starting with previous word
- Continue until </s> is picked
Language Model Evaluation
Test data
| For smaller corpora | For large corpora (typical for text) | |
|---|---|---|
| Train | 80% Train | 98% |
| Validation | 10% Validation | 1% |
| Test | 10% Validation | 1% |
●split method
对于连续的文本

对于Random short sequences

Perplexity
Perplexity(困惑度)是自然语言处理中用来衡量语言模型好坏的一个指标,特别是在评估语言模型对文本的预测能力时。Perplexity的公式通常表示为:
markdown
PP ( W ) = P ( w 1 , w 2 , . . . , w m ) − 1 m \text{PP}(W) = P(w_1 ,w_2 ,...,w_m)^{-\frac{1}{m}} PP(W)=P(w1,w2,...,wm)−m1
其中:
P ( w 1 , w 2 , . . . , w m ) P(w_1 ,w_2 ,...,w_m) P(w1,w2,...,wm)是语言模型对观测到的词序列的概率的乘积
m m m 是词序列中的词的总数。
具体来说, P ( w 1 , w 2 , . . . , w N ) P(w_1 ,w_2 ,...,w_N) P(w1,w2,...,wN) 可以展开为:
P ( w 1 , w 2 , . . . , w N ) = ∏ i = 1 N P ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) P(w_1, w_2, ..., w_N) = \prod_{i=1}^{N} P(w_i | w_1, w_2, ..., w_{i-1}) P(w1,w2,...,wN)=i=1∏NP(wi∣w1,w2,...,wi−1)
这里:
w i w_i wi表示序列中的第 i i i 个词。
P ( w i ∣ w − 1 , w 2 , . . . , w i − 1 ) P(w_ i ∣w-1 ,w_2 ,...,w_{i−1} ) P(wi∣w−1,w2,...,wi−1) 是给定前 i − 1 i−1 i−1 个词的情况下,第 i i i 个词出现的概率。
Perplexity的计算公式中的 P − 1 N P^{-\frac{1}{N}} P−N1 表示的是所有词的概率的几何平均值的倒数。几何平均值可以看作是所有概率乘积的N次方根,而取倒数是为了将平均值转换为原始概率的尺度。
困惑度越低,表示语言模型对数据的预测越准确,即模型对词序列的预测越不困惑。在实践中,一个低困惑度的语言模型意味着它能够更好地预测下一个词,从而生成更自然、更连贯的句子。
Smaller perplexity = better model
Character level models PP < word based models PP
Perplexity for bigram models
P P ( W ) = ∏ i = 1 m ∏ j = 1 ∣ s i ∣ 1 P ( w j ( i ) ∣ w j − 1 ( i ) ) m PP(W)=\sqrt[m]{\prod_{i=1}^m\prod_{j=1}^{|s_i|}\cfrac{1}{P(w_j^{(i)}|w_{j-1}^{(i)})}} PP(W)=mi=1∏mj=1∏∣si∣P(wj(i)∣wj−1(i))1
w j ( i ) w_j^{(i)} wj(i)表示第i个句子中的第j个词
concatenate all sentences in W
然后计算bigram模型的困惑度,需要计算所有句子的bigram概率的乘积,然后取幂次-1/m
P P ( W ) = ∏ i = 1 m 1 P ( w i ∣ w i − 1 ) m PP(W)=\sqrt[m]{\prod_{i=1}^m\cfrac{1}{P(w_i|w_{i-1})}} PP(W)=mi=1∏mP(wi∣wi−1)1
w i w_{i} wi表示test set中第i个词
Log perplexity
同样将乘法变成加法:
log P P ( W ) = 1 m ∑ i = 1 m log 2 ( P ( w i ∣ w i − 1 ) ) \log PP(W)=\cfrac{1}{m}\sum_{i=1}^m\log_2(P(w_i|w_{i-1})) logPP(W)=m1i=1∑mlog2(P(wi∣wi−1))
Example

Training 38 million words, test 1.5 million words, WSJ corpus
Perplexity Unigram: 962 Bigram: 170 Trigram: 109
WSJ corpus,全称为Wall Street Journal (WSJ) Corpus,是一个广泛使用的文本语料库,它基于《华尔街日报》的文本内容。这个语料库在自然语言处理(NLP)领域非常知名,特别是用于语言模型的训练和评估。
Out of Vocabulary Words
Out of vocabulary words
Closed vs. Open vocabularies
封闭词汇表提供了一种简化的方法来处理文本,但可能会牺牲对新词的处理能力;而开放词汇表提供了更大的灵活性,可以更好地适应多样化的语言使用,但可能会增加模型的复杂性和计算成本。
Closed Vocabularies(封闭词汇表):
在封闭词汇表系统中,模型在训练前定义了一个固定的词汇集,这个词汇集包含了所有在模型训练和预测时会用到的单词或标记(tokens)。
任何不在词汇表中的词在处理时通常会被忽略或替换为一个特殊的未知标记(如<UNK>)。
封闭词汇表有助于减少模型的复杂性,因为它限制了模型需要学习和预测的词汇数量。
这种方法的一个缺点是,它无法很好地处理词汇表之外的新词或罕见词,这可能会影响模型对新文本的理解能力。
Open Vocabularies(开放词汇表):
开放词汇表系统不限制模型使用的词汇数量。模型可以处理任何它遇到的词,无论这些词是否在训练数据中出现过。
在这种设置下,模型通常使用子词分割(subword segmentation)技术,如Byte Pair Encoding(BPE)或WordPiece,来处理不在训练集中的词。
开放词汇表可以更好地处理多样化的文本,包括专业术语或新出现的词汇,因为它们不会被简单地替换为未知标记。
然而,这种方法可能会增加模型的复杂性,因为模型需要学习更多的词汇和它们之间的关系。
Unknown word = Out of vocabulary word (OOV)
special tag <UNK> in corpus and in input
Using <UNK> in corpus
步骤:
● Create vocabulary V
● Replace any word in corpus and not in V by <UNK>
● Count the probabilities with <UNK> as with any other word
例子:
Corpus
<s> Lyn drinks chocolate </s>
<s> John drinks tea </s>
<s> Lyn eats chocolate </s>
将词表门槛定为最少出现两次:Min frequency f=2
<s> Lyn drinks chocolate </s>
<s> <UNK> drinks <UNK> </s>
<s> Lyn <UNK> chocolate </s>
最后的词表为:
Vocabulary
Lyn, drinks, chocolate
在进行输入查询时,如果有非词表的单词,也要替换为UNK
<s>Adam drinks chocolate</s>
<s><UNK> drinks chocolate</s>
How to create vocabulary V
两种条件:
- 设定单词最小出现频率,大于该频率的进入词表,否则设置为UNK
- 设定词表最大容量 ∣ V ∣ |V| ∣V∣,按单词出现频率排序,将前 ∣ V ∣ |V| ∣V∣个单词包含进词表,其他的设置为UNK
虽然UNK对于降低困惑度有效,但不建议设置过多的UNK词,否则在你生成句子的时候会看到很多的UNK
在比较困惑度的时候,only compare LMs with the same V
Quiz
Given the training corpus and minimum word frequency=2, how would the vocabulary for corpus
preprocessed with <UNK> look like?
“<s> I am happy I am learning </s> <s> I am happy I can study </s>”
Answer:
V = (I,am,happy)
Smoothing
Missing N-grams in training corpus
Problem: N-grams made of known words still might be missing in the training corpus
如何处理由语料库中出现的单词组成但Ngram本身不存在的N-gram的概率
例如,语料库有“John”,“eats”,但是没有“John eats”,此时“John eats”的计数为0,其bigram概率也为0,会导致整个句子出现概率也为0
Smoothing
Add-one smoothing (Laplacian smoothing)
P ( w n ∣ w n − 1 ) = C ( w n − 1 , w n ) + 1 ∑ w ∈ V ( C ( w n − 1 , w n ) + 1 ) = C ( w n − 1 , w n ) + 1 C ( w n − 1 ) + V P(w_n|w_{n-1})=\cfrac{C(w_{n-1},w_n)+1}{\sum_{w\in V}(C(w_{n-1},w_n)+1)}=\cfrac{C(w_{n-1},w_n)+1}{C(w_{n-1})+V} P(wn∣wn−1)=∑w∈V(C(wn−1,wn)+1)C(wn−1,wn)+1=C(wn−1)+VC(wn−1,wn)+1
Add-one smoothing需要在词表足够大的情况下使用,否则会使得缺失单词概率过高。
如果语料库非常大,则可以使用Add k smoothing(可用在3gram、4gram等高阶gram上):
P ( w n ∣ w n − 1 ) = C ( w n − 1 , w n ) + k ∑ w ∈ V ( C ( w n − 1 , w n ) + k ) = C ( w n − 1 , w n ) + k C ( w n − 1 ) + k × V P(w_n|w_{n-1})=\cfrac{C(w_{n-1},w_n)+k}{\sum_{w\in V}(C(w_{n-1},w_n)+k)}=\cfrac{C(w_{n-1},w_n)+k}{C(w_{n-1})+k\times V} P(wn∣wn−1)=∑w∈V(C(wn−1,wn)+k)C(wn−1,wn)+k=C(wn−1)+k×VC(wn−1,wn)+k
Advanced methods:
Kneser-Ney Smoothing(Kneser-Ney 平滑):
Kneser-Ney 由 Reinhard Kneser 和 Hermann Ney 提出,是一种用于计算条件概率分布的平滑技术。
它通过调整概率分布,使得低频词或未见词的概率分布更加均匀,从而提高语言模型的泛化能力。
Kneser-Ney 考虑了词的上下文,通过加权平均的方式来更新概率,其中权重取决于词在语料库中的相对频率。
它特别适合处理大规模语料库,因为它可以有效地利用语料中的统计信息。
Good-Turing Smoothing(Good-Turing 平滑):
Good-Turing smoothing 是由I. J. Good提出的,用于估计在语料库中未出现过的词的概率。
它基于一个简单的统计观察:在语料库中出现一次的词的数量大约是出现多次的词的数量的一半。
Good-Turing 方法通过将概率质量从高频词转移到低频词来实现平滑,特别是对于那些在训练语料中未出现过的词。
这种方法简单且计算效率高,但可能不如 Kneser-Ney 方法那样灵活,因为它不区分不同上下文中的词。
两种平滑方法各有优势和局限性。Kneser-Ney smoothing 通常在实际应用中表现更好,因为它考虑了词的上下文信息,但计算复杂度较高。Good-Turing smoothing 则因其简单性和效率而在某些情况下被采用,尤其是在资源受限的情况下。
Backoff
If N-gram missing => use (N-1)-gram, …有两种backoff方式
第一种是直接替换:Probability discounting e.g. Katz backoff
第二种是乘以某个常数(0.4比较好)后替换:“Stupid” backoff

Interpolation
Interpolation(插值)是一种在自然语言处理中用于平滑语言模型的技术,特别是在处理不同概率分布的组合时。它通过将多个模型或分布的输出以某种方式结合起来,以减少模型的不确定性和过拟合,同时提高泛化能力。最常见的插值方法是线性插值,它简单地将不同模型的概率输出按照一定的权重进行加权平均。

系数 λ \lambda λ可以通过训练来确定
Quiz
Question:
Corpus: “I am happy I am learning”
In the context of our corpus, what is the estimated probability of word “can” following the word “I” using the
bigram model and add k smoothing where k=3.
Answer:
P(can|I)=P(can|I) = 3/(2+3×4)
相关文章:

08.C2W3.Auto-complete and Language Models
往期文章请点这里 目录 N-Grams: OverviewN-grams and ProbabilitiesN-gramsSequence notationUnigram probabilityBigram probabilityTrigram ProbabilityN -gram probabilityQuiz Sequence ProbabilitiesProbability of a sequenceSequence probability shortcomingsApproxi…...

【linux】log 保存和过滤
log 保存 ./run.sh 2>&1 | tee -a /home/name/log.txt log 过滤 import os import re# Expanded regular expression to match a wider range of error patterns error_patterns re.compile(# r(error|exception|traceback|fail|failed|fatal|critical|warn|warning…...
GeoTrust ——适合企业使用的SSL证书!
GeoTrust是一家全球知名的数字证书颁发机构(CA),其提供的SSL证书非常适合企业使用。GeoTrust的SSL证书为企业带来了多重优势,不仅在验证级别、加密强度、兼容性、客户服务等方面表现出色,而且其高性价比和灵活的证书选…...

Kubelet 认证
当我们执行kubectl exec -it pod [podName] sh命令时,apiserver会向kubelet发起API请求。也就是说,kubelet会提供HTTP服务,而为了安全,kubelet必须提供HTTPS服务,且还要提供一定的认证与授权机制,防止任何知…...

aws slb
NLB 目标组 Target is in an Availability Zone that is not enabled for the load balancer 解决: https://docs.aws.amazon.com/zh_cn/elasticloadbalancing/latest/network/load-balancer-troubleshooting.html 负载均衡器添加 后端EC2 所在的vpc网段即可。…...

【AI大模型】ChatGPT-4 对比 ChatGPT-3.5:有哪些优势
引言 ChatGPT4相比于ChatGPT3.5,有着诸多不可比拟的优势,比如图片生成、图片内容解析、GPTS开发、更智能的语言理解能力等,但是在国内使用GPT4存在网络及充值障碍等问题,如果您对ChatGPT4.0感兴趣,可以私信博主为您解决账号和环境…...

详解yolov5的网络结构
转载自文章 网络结构图(简易版和详细版) 此图是博主的老师,杜老师的图 网络框架介绍 前言: YOLOv5是一种基于轻量级卷积神经网络(CNN)的目标检测算法,整体可以分为三个部分, ba…...

汽车零配件行业看板管理系统应用
生产制造已经走向了精益生产,计算时效产出、物料周转时间等问题,成为每一个制造企业要面临的问题,工厂更需要加快自动化,信息化,数字化的布局和应用。 之前的文章多次讲解了企业MES管理系统,本篇文章就为大…...

【Go】函数的使用
目录 函数返回多个值 init函数和import init函数 main函数 函数的参数 值传递 引用传递(指针) 函数返回多个值 用法如下: package mainimport ("fmt""strconv" )// 返回多个返回值,无参数名 func Mu…...

宝塔面板运行Admin.net框架
准备 宝塔安装 .netcore安装 Admin.net框架发布 宝塔面板设置 完结撒花 1.准备 服务器/虚拟机一台 系统Windows server / Ubuntu20.04(本贴使用的是Ubuntu20.04版本系统) Admin.net开发框架 先安装好服务器系统,这里就不做安装过程描述了&…...
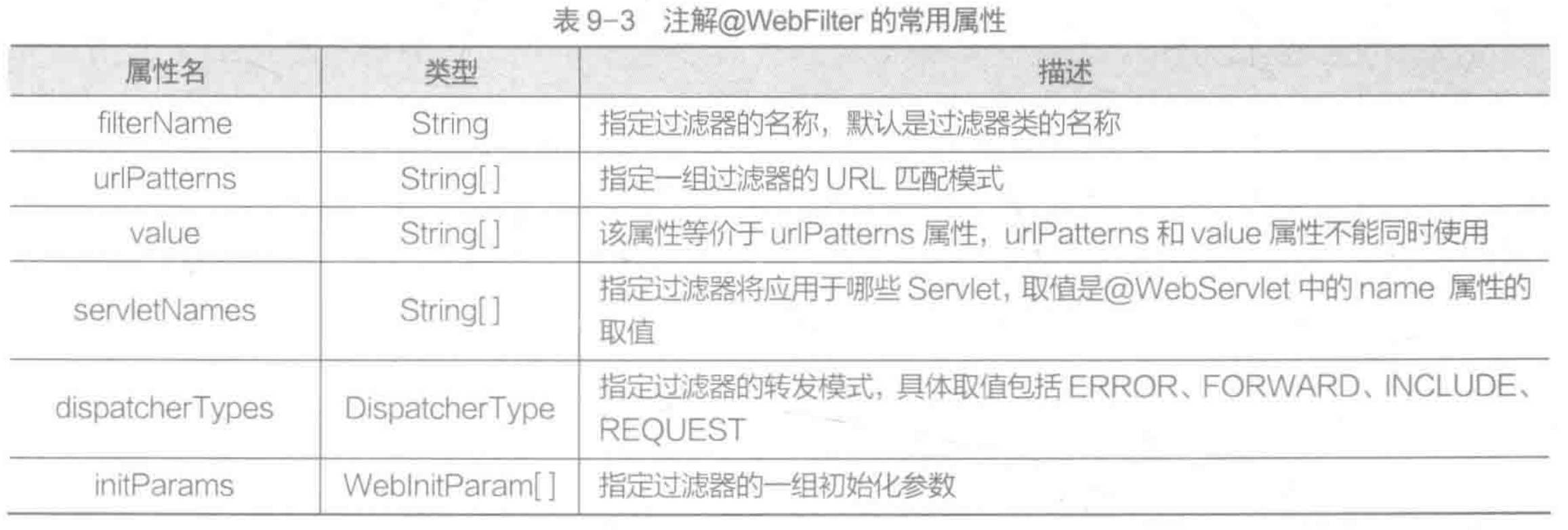
Javaweb11-Filter过滤器
Filter过滤器 1.Filter的基本概念: 在Java Servlet中,Filter接口是用来处理HttpServletRequest和HttpServletResponse的对象的过滤器。主要用途是在请求到达Servlet之前或者响应离开Servlet之前对请求或响应进行预处理或后处理。 2.Filter常见的API F…...

【AI-7】CUDA
CUDA(Compute Unified Device Architecture)是NVIDIA公司开发的一种并行计算平台和编程模型,使开发者能够利用NVIDIA GPU的强大计算能力来加速各种应用。以下是关于CUDA的详细介绍: CUDA的特点 并行计算:CUDA允许开发…...

ctfshow-web入门-文件上传(web164、web165)图片二次渲染绕过
web164 和 web165 的利用点都是二次渲染,一个是 png,一个是 jpg 目录 1、web164 2、web165 二次渲染: 网站服务器会对上传的图片进行二次处理,对文件内容进行替换更新,根据原有图片生成一个新的图片,这样…...

基于实现Runnable接口的java多线程
Java多线程通常可以通过继承Thread类或者实现Runnable接口实现。本文主要介绍实现Runnable接口的java多线程的方法, 并通过ThreadPoolTaskExecutor调用执行,以及应用场景。 一、应用场景 异步、并行、子任务、磁盘读写、数据库查询、网络请求等耗时操作等。 以下…...

如何在uniapp中使用websocket?
websocket是我们经常使用到的接口,通常用于即时通讯以及K线图这种需要实时更新数据的业务需求上,传统的restful接口虽然可以满足,但是你需要轮询,这就要额外写一堆代码,不是很方便,用websocket就简单很多,我们来看代码 第一步定义全局常量、变量 const config = {host…...

PCL 点云PFH特征描述子
点云PFH特征描述子 一、概述1.1 概念1.2 算法原理二、代码实现三、结果示例一、概述 1.1 概念 点特征直方图PFH(Point Feature Histograms)描述子:用于表示点云中每个点的局部几何形状信息,它是一种直方图描述子,包括了点云的法线方向和曲率信息,PFH描述子可以帮助区分不同…...

linux程序安装-编译-rpm-yum
编译安装流程步骤详解 识途老码 | Linux编译安装程序 编译安装概览 编译安装是从软件的源代码构建到最终安装的过程,它允许用户根据自身的需求和系统的环境来自定义软件的配置和功能。相对于二进制安装,编译安装提供了更高的灵活性和控制能力,但同时也要求用户具备一定的…...

【网络协议】PIM
PIM 1 基本概念 PIM(Protocol Independent Multicast)协议,即协议无关组播协议,是一种组播路由协议,其特点是不依赖于某一特定的单播路由协议,而是可以利用任意单播路由协议建立的单播路由表完成RPF&…...
基本介绍)
Redis 中的跳跃表(Skiplist)基本介绍
Redis 中的跳跃表(Skiplist)是一种用于有序元素集合的快速查找数据结构。它通过一个多级索引来提高搜索效率,能够在对数时间复杂度内完成查找、插入和删除操作。跳跃表特别适用于实现有序集合(sorted set)的功能&#…...

C语言编译和编译预处理
1.编译预处理 • 编译是指把高级语言编写的源程序翻译成计算机可识别的二进制程序(目标程序)的过程,它由编译程序完成。 • 编译预处理是指在编译之前所作的处理工作,它由编译预处理程序完成 在对一个源程序进行编译时࿰…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
