线性代数|机器学习-P23梯度下降
文章目录
- 1. 梯度下降[线搜索方法]
- 1.1 线搜索方法,运用一阶导数信息
- 1.2 经典牛顿方法,运用二阶导数信息
- 2. hessian矩阵和凸函数
- 2.1 实对称矩阵函数求导
- 2.2. 线性函数求导
- 3. 无约束条件下的最值问题
- 4. 正则化
- 4.1 定义
- 4.2 性质
- 5. 回溯线性搜索法
1. 梯度下降[线搜索方法]
我们之前经常用到的梯度下降,
1.1 线搜索方法,运用一阶导数信息
- 迭代公式:
x k + 1 = x k − s k ∇ f ( x k ) \begin{equation} x_{k+1}=x_k-s_k\nabla f(x_k) \end{equation} xk+1=xk−sk∇f(xk) - 步长: s k s_k sk,也叫学习率
- 方向: − ∇ f ( x k ) -\nabla f(x_k) −∇f(xk)负梯度方向
1.2 经典牛顿方法,运用二阶导数信息
详细推导请点击链接
- 迭代公式:
x k + 1 = x k − [ H j k ] − 1 ∇ f ( x ) \begin{equation} x_{k+1}=x_k-[H_{jk}]^{-1}\nabla f(x) \end{equation} xk+1=xk−[Hjk]−1∇f(x) - 步长: s k = 1 s_k=1 sk=1,把步长和方向结合起来放到方向里面去了。
- 方向:
hessian matrix 可逆时[ H j k ] − 1 ∇ f ( x ) [H_{jk}]^{-1}\nabla f(x) [Hjk]−1∇f(x)
2. hessian矩阵和凸函数
- 如果
hessian matrixH j k H_{jk} Hjk是半正定矩阵[positive semi-definite]或正定矩阵[positive definite]可得为函数是一般凸函数 - 如果
hessian matrixH j k H_{jk} Hjk是正定矩阵[positive definite]可得为函数是强凸函数
2.1 实对称矩阵函数求导
假设我们有一个实对称矩阵S和二次型函数表示如下:
S = [ 1 0 0 b ] , f ( x ) = 1 2 x T S x = 1 2 ( x 2 + b y 2 ) \begin{equation} S=\begin{bmatrix}1&0\\\\0&b\end{bmatrix},f(x)=\frac{1}{2}x^TSx=\frac{1}{2}(x^2+by^2) \end{equation} S= 100b ,f(x)=21xTSx=21(x2+by2)
- 矩阵S的特征值,条件数 κ ( S ) \kappa(S) κ(S)分别表示如下,假设 b < 1 b<1 b<1:
λ max = 1 , λ min = b , κ ( S ) = 1 b \begin{equation} \lambda_{\max}=1,\lambda_{\min}=b,\kappa(S)=\frac{1}{b} \end{equation} λmax=1,λmin=b,κ(S)=b1 - 通过 f ( x ) f(x) f(x)函数可以明显看出最小值点为(0,0)
arg min x ∗ = 0 f ( x ) = 0 \begin{equation} \argmin \limits_{x^*=0}f(x)=0 \end{equation} x∗=0argminf(x)=0 - 函数一阶导数如下:
d f ( x , y ) d X = d 1 2 X T S X d X = S X = [ 1 0 0 b ] [ x y ] = [ x b y ] \begin{equation} \frac{\mathrm{d}f(x,y)}{\mathrm{d}X}=\frac{\mathrm{d}\frac{1}{2}X^TSX}{\mathrm{d}X}=SX=\begin{bmatrix}1&0\\\\0&b\end{bmatrix}\begin{bmatrix}x\\\\y\end{bmatrix}=\begin{bmatrix}x\\\\by\end{bmatrix} \end{equation} dXdf(x,y)=dXd21XTSX=SX= 100b xy = xby - 函数二阶导数如下:
d 2 f ( x , y ) d X 2 = S = [ 1 0 0 b ] \begin{equation} \frac{\mathrm{d}^2f(x,y)}{\mathrm{d}X^2}=S=\begin{bmatrix}1&0\\\\0&b\end{bmatrix} \end{equation} dX2d2f(x,y)=S= 100b
2.2. 线性函数求导
假设我们有如下函数:
f ( x , y ) = 2 x + 5 y = [ 2 5 ] [ x y ] = A T X , A = [ 2 5 ] \begin{equation} f(x,y)=2x+5y=\begin{bmatrix}2&5\end{bmatrix}\begin{bmatrix}x\\\\y\end{bmatrix}=A^TX,A=\begin{bmatrix}2\\\\5\end{bmatrix} \end{equation} f(x,y)=2x+5y=[25] xy =ATX,A= 25
- 函数的一次导数如下:
d f ( x , y ) d X = d A T X d X = A = [ 2 5 ] \begin{equation} \frac{\mathrm{d}f(x,y)}{\mathrm{d}X}=\frac{\mathrm{d}A^TX}{\mathrm{d}X}=A=\begin{bmatrix}2\\\\5\end{bmatrix} \end{equation} dXdf(x,y)=dXdATX=A= 25 - 函数的二阶偏导
hessian matrix如下:[向量对向量求导,XY拉伸术]
H j k = [ 0 0 0 0 ] \begin{equation} H_{jk}=\begin{bmatrix}0&0\\\\0&0\end{bmatrix} \end{equation} Hjk= 0000 - 对于函数 f ( x ) = 2 x + 5 y f(x)=2x+5y f(x)=2x+5y来说,依据线搜索方法,其负梯度方向为最佳迭代方向。
3. 无约束条件下的最值问题
假设我们有一个函数表示如下:
f ( x ) = 1 2 x T S x − a T x − b \begin{equation} f(x)=\frac{1}{2}x^TSx-a^Tx-b \end{equation} f(x)=21xTSx−aTx−b
- f ( x ) f(x) f(x)导数如下:
d f ( x ) d x = S x − a ; d 2 f ( x ) d x 2 = H j k = S \begin{equation} \frac{\mathrm{d}f(x)}{\mathrm{d}x}=Sx-a;\frac{\mathrm{d}^2f(x)}{\mathrm{d}x^2}=H_{jk}=S \end{equation} dxdf(x)=Sx−a;dx2d2f(x)=Hjk=S - 函数 f ( x ) f(x) f(x)的最小值满足其一次导数为零,即表示如下:
f ′ ( x ∗ ) = 0 , S x ∗ − a = 0 → x ∗ = S − 1 a \begin{equation} f'(x^*)=0,Sx^*-a=0\rightarrow x^*=S^{-1}a \end{equation} f′(x∗)=0,Sx∗−a=0→x∗=S−1a - 整理可得:
f min ( x ) = min x = x ∗ = S − 1 a f ( x ) = − 1 2 a T S − 1 a − b \begin{equation} f_{\min}(x)=\min\limits_{x=x^*=S^{-1}a}f(x)=-\frac{1}{2}a^TS^{-1}a-b \end{equation} fmin(x)=x=x∗=S−1aminf(x)=−21aTS−1a−b
arg min x = x ∗ f ( x ) = S − 1 a \begin{equation} \argmin\limits_{x=x^*}f(x)=S^{-1}a \end{equation} x=x∗argminf(x)=S−1a
4. 正则化
4.1 定义
- Log-determinant regularization
Log-determinant regularization 通过在损失函数中加入一个负对数行列式项来约束矩阵X的结构。具体形式为
P e n a l t y = − log ( det ( X ) ) \begin{equation} Penalty=-\log(\det(X)) \end{equation} Penalty=−log(det(X)) - 其中X通常是一个正定矩阵, 这一正则化项有利于确保X的特征值远离零,从而避免数值不稳定性和病态矩阵的出现
4.2 性质
- 凸性: − log ( det ( X ) ) -\log(\det(X)) −log(det(X))是一个凸函数,这意味着优化问题中,局部最小值也是全局最小值
- 梯度: ∇ f ( x ) = − X − 1 \nabla f(x)=-X^{-1} ∇f(x)=−X−1
f ( x ) = − log ( det ( X ) ) → d f ( x ) d x = 1 det ( X ) ⋅ [ det ( X ) ⋅ ( X − 1 ) T ] = X − 1 \begin{equation} f(x)=-\log(\det(X))\rightarrow \frac{\mathrm{d}f(x)}{\mathrm{d}x}=\frac{1}{\det(X)}\cdot [\det(X)\cdot (X^{-1})^T]=X^{-1} \end{equation} f(x)=−log(det(X))→dxdf(x)=det(X)1⋅[det(X)⋅(X−1)T]=X−1 hessian matrix:
H j k = X − 1 H X − 1 , H 是一个对称矩阵 \begin{equation} H_{jk}=X^{-1}HX^{-1},H是一个对称矩阵 \end{equation} Hjk=X−1HX−1,H是一个对称矩阵
5. 回溯线性搜索法
对于线搜索方法来说,迭代公式如下,但是对于步长的选择来说,我们如果选择步长 s k s_k sk太大,那么就很容易越过极值点,在极值点不断跳跃和震荡,如果步长 s k s_k sk太小,那么迭代太慢,没有效果
- 迭代公式:
x k + 1 = x k − s k ∇ f ( x k ) \begin{equation} x_{k+1}=x_k-s_k\nabla f(x_k) \end{equation} xk+1=xk−sk∇f(xk) - 步长: s k s_k sk
- 方向: 负梯度方向 − ∇ f ( x k ) -\nabla f(x_k) −∇f(xk)
那么我们希望找到一个步长 s k s_k sk使得在搜索方向上使得 f ( x k + 1 ) f(x_{k+1}) f(xk+1)最小,这样就不是固定步长了,相当于动态步长
s k ∗ = arg min s k f ( x k + 1 ) \begin{equation} s_k^*= \argmin\limits_{s_k} f(x_{k+1}) \end{equation} sk∗=skargminf(xk+1)
- 步骤:先固定步长 s k = s 0 s_k=s_0 sk=s0,再取半步长 s k = 1 2 s 0 s_k=\frac{1}{2}s_0 sk=21s0,再取半步长 s k = 1 4 s 0 s_k=\frac{1}{4}s_0 sk=41s0,
- 假设我们有如下一个损失函数如下:
S = [ 1 0 0 b ] , f ( x ) = x T S x = x 2 + b y 2 \begin{equation} S=\begin{bmatrix}1&0\\\\0&b\end{bmatrix},f(x)=x^TSx=x^2+by^2 \end{equation} S= 100b ,f(x)=xTSx=x2+by2 - 迭代公式如下:
x k + 1 = x k − s k ∇ f ( x k ) , ∇ f ( x k ) = 2 S x \begin{equation} x_{k+1}=x_k-s_k\nabla f(x_k),\nabla f(x_k)=2Sx \end{equation} xk+1=xk−sk∇f(xk),∇f(xk)=2Sx - 向量化如下 : x = [ x , y ] T x\;=[x\;,y\;]^T x=[x,y]T
[ x y ] k + 1 = [ x y ] k − s k [ 2 x 2 b y ] k \begin{equation} \begin{bmatrix}x\\\\y\end{bmatrix}_{k+1}=\begin{bmatrix}x\\\\y\end{bmatrix}_{k}-s_k\begin{bmatrix}2x\\\\2by\end{bmatrix}_{k} \end{equation} xy k+1= xy k−sk 2x2by k - 假设我们定义初始点 p 0 = ( x 0 , y 0 ) = ( b , 1 ) p_0=(x_0,y_0)=(b,1) p0=(x0,y0)=(b,1)
- 步长 s k = 1 x 0 + y 0 = 1 b + 1 s_k=\frac{1}{x_0+y_0}=\frac{1}{b+1} sk=x0+y01=b+11
这里没弄懂,后续再研究,反推出来的
x k = b ( b − 1 b + 1 ) k , y k = ( 1 − b 1 + b ) k , f k = ( 1 − b 1 + b ) k f 0 \begin{equation} x_k=b(\frac{b-1}{b+1})^k,y_k=(\frac{1-b}{1+b})^k,f_k=(\frac{1-b}{1+b})^kf_0 \end{equation} xk=b(b+1b−1)k,yk=(1+b1−b)k,fk=(1+b1−b)kf0 - 函数 f ( x ) = x 2 + b y 2 = c f(x)=x^2+by^2=c f(x)=x2+by2=c是一个椭圆形图像,随着c的变化不断变化,也就是做函数的最小值是
之字型不断地趋近于最小,就像不同的椭圆进行等比缩小,最终求得最小值。

相关文章:

线性代数|机器学习-P23梯度下降
文章目录 1. 梯度下降[线搜索方法]1.1 线搜索方法,运用一阶导数信息1.2 经典牛顿方法,运用二阶导数信息 2. hessian矩阵和凸函数2.1 实对称矩阵函数求导2.2. 线性函数求导 3. 无约束条件下的最值问题4. 正则化4.1 定义4.2 性质 5. 回溯线性搜索法 1. 梯度…...

SQL,python,knime将数据混合的文字数字拆出来,合并计算实战
将下面将数据混合的文字数字拆出来,合并计算 一、SQL解决: ---创建表插入数据 CREATE TABLE original_data (id INT AUTO_INCREMENT PRIMARY KEY,city VARCHAR(255),value DECIMAL(10, 2) );INSERT INTO original_data (city, value) VALUES (上海0.5…...

mac ssh连接工具
在Mac上,有多个SSH连接工具可供选择,这些工具根据其功能和适用场景的不同,可以满足不同用户的需求。以下是一些推荐的SSH客户端软件:12 iTerm2:这是一款功能强大的终端应用程序,提供了丰富的功能和定制选项…...
阿里通义音频生成大模型 FunAudioLLM 开源
简介 近年来,人工智能(AI)技术的进步极大地改变了人类与机器的互动方式,特别是在语音处理领域。阿里巴巴通义实验室最近开源了一个名为FunAudioLLM的语音大模型项目,旨在促进人类与大型语言模型(LLMs&…...
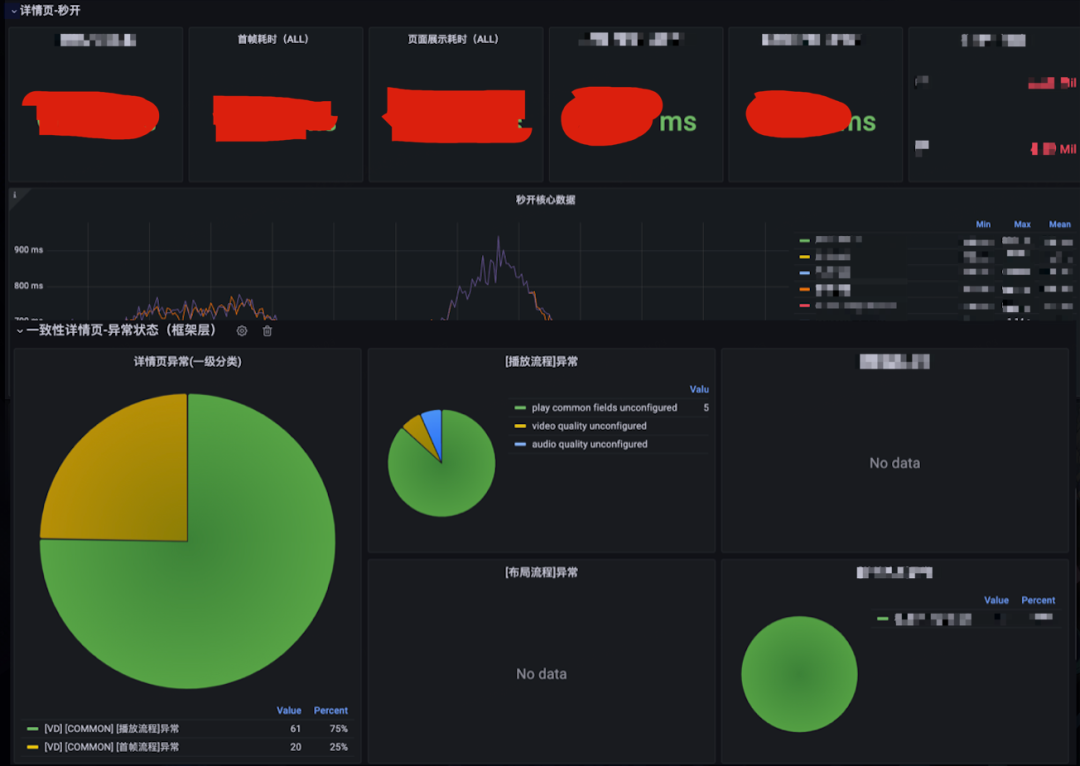
通用详情页的打造
背景介绍 大家都知道,详情页承载了站内的核心流量。它的量级到底有多大呢? 我们来看一下,日均播放次数数亿次,这么大的流量,其重要程度可想而知。 在这样一个页面,每一个功能都是大量业务的汇总点。 作为…...

java内部类的本质
定义在类内部,可以实现对外部完全隐藏,可以有更好的封装性,代码实现上也往往更为简洁。 内部类可以方便地访问外部类的私有变量,可以声明为private从而实现对外完全隐藏。 在Java中,根据定义的位置和方式不同…...

vue3 学习笔记08 -- computed 和 watch
vue3 学习笔记08 – computed 和 watch computed computed 是 Vue 3 中用于创建计算属性的重要 API,它能够根据其它响应式数据动态计算出一个新的值,并确保在依赖数据变化时自动更新。 基本用法 squaredCount 是一个计算属性,它依赖于 count…...

Python-PLAXIS自动化建模技术与典型岩土工程案例
有限单元法在岩土工程问题中应用非常广泛,很多软件都采用有限单元解法。在使用各大软件进行数值模拟建模的过程中,岩土工程中的各种问题(塑性、渗流、固结、动力、稳定安全、热力TM),一步一步地搭建自己的Plaxis模型&a…...

license系统模型设计使用django models
User (用户)License (许可证)Product (产品)LicenseAssignment (许可证分配) 简单的模型定义: from django.db import models from django.contrib.auth.models import Userclass Product(models.Model):name models.CharField(max_length255)description model…...

【通信协议-RTCM】MSM语句(1) - 多信号GNSS观测数据消息格式
注释: RTCM响应消息1020为GLONASS星历信息,暂不介绍,前公司暂未研发RTCM消息类型版本的DR/RTK模块,DR/RTK模块仅NMEA消息类型使用 注释: 公司使用的多信号语句类型为MSM4&MSM7,也应该是运用最广泛的语句…...

vue3-vite-pinia模板
模板说明 下载 git clone https://github.com/AIxiaoHanBao/vue-template.gitmodule参数 node版本 16 UI组件库 element-plus 持久化 pinia 网络请求 axios 路由 vue-router 使用说明 权限管理目录access资源目录assets组件目录components页面目录pages网络请求目录re…...

华为HCIP Datacom H12-821 卷38
1.多选题 下面关于 BGP中的公认属性的描述,正确的是 A、公认必遵属性是所有BGP路由器都识别,且必须存在于Updata消息中心 B、BGP必须识别所有公认属性 C、公认属性分为公认必遵和可选过渡两种 D、公认任意属性是所有BGP造由器都可以识别,…...

C语言求10进制转2进制(除2取余法)
1.思路:除2取余法,也就是说用除以2取余来将10进制数转换为二进制 2.两种代码实现,这里用了两,一个递归一个非递归。 递归是一种编程技术,其中一个函数直接或间接地调用自己。递归通常用于解决那些可以被分解为更小的、…...

PHP 调用淘宝详情 API 接口的方法与实践
以下是关于“PHP 调用淘宝详情 API 接口的方法与实践”的一篇文章示例: PHP 调用淘宝详情 API 接口的方法与实践 在当今的电商时代,获取淘宝商品的详情信息对于许多开发者来说是一项重要的任务。使用 PHP 语言来调用淘宝详情 API 接口,可以…...

风景区服务热线系统:智能化时代的旅游新选择
一、引言 1 、风景区服务热线系统的概念 风景区服务热线系统是指为游客提供实时旅游信息咨询、投诉处理、紧急救援等一系列服务的电话和网络平台。它不仅是景区与游客之间的重要沟通桥梁,也是提升游客满意度、优化景区管理的重要手段。 2 、智能化时代对旅游服务…...

Linux修改配置文件后无法使用命令或无法进入桌面
如果你是修改了配置文件,如 sudo vim /etc/profile重启无数次发现无法进入桌面,不要着急重装系统!!,怎么造成的怎么改就行了 以下方案需要root密码,忘记密码详见:Linux忘记root密码怎么办 一…...
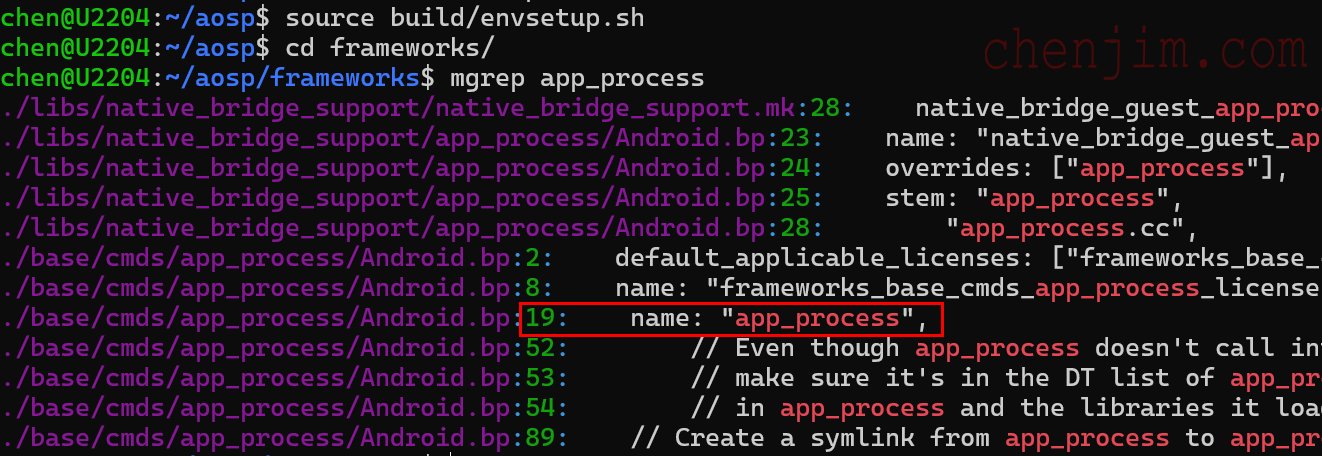
安卓14中Zygote初始化流程及源码分析
文章目录 日志抓取结合日志与源码分析systemServer zygote创建时序图一般应用 zygote 创建时序图向 zygote socket 发送数据时序图 本文首发地址 https://h89.cn/archives/298.html 最新更新地址 https://gitee.com/chenjim/chenjimblog 本文主要结合日志和代码看安卓 14 中 Zy…...

等保一体机 | 什么是等保一体机?一台机器就能过等保吗?
什么是等保一体机? 对于中小型企业来说,他们在接触到等保的条件下,可能会觉得成本太高了,毕竟整改的时候,几台安全设备下来报价就几十w。 也许有些人会听说过等保一体机 那么什么是等保一体机呢? 等保一…...

【活动预告】Apache IoTDB TsFile 智慧能源应用“上会”啦!
2024 年,站在中国数字经济产业升级和数据要素市场化建设的时代交汇点上,为进一步推动全球数据库产业进步,由中国通信标准化协会、大数据技术标准推进委员会主办的“2024 可信数据库发展大会”将于 2024 年 7 月 16-17 日,在北京朝…...

【公益案例展】中国电信安全大模型——锻造安全行业能量转化的高性能引擎...
电信安全公益案例 本项目案例由电信安全投递并参与数据猿与上海大数据联盟联合推出的 #榜样的力量# 《2024中国数智产业最具社会责任感企业》榜单/奖项评选。 大数据产业创新服务媒体 ——聚焦数据 改变商业 以GPT系列为代表的大模型技术,展现了人工智能技术与应…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
