【基于R语言群体遗传学】-16-中性检验Tajima‘s D及连锁不平衡 linkage disequilibrium (LD)
Tajima's D Test
已经开发了几种中性检验,用于识别模型假设的潜在偏差。在这里,我们将说明一种有影响力的中性检验,即Tajima's D(Tajima 1989)。Tajima's D通过比较数据集中的两个𝜃 = 4N𝜇估计值来工作。我们已经推导出了𝜃is,等于平均成对杂合性(average pairwise heterozygosity),当我们讨论共祖时(也称为Tajima的估计器)。当考虑DNA序列集合中的等位基因或SNP总数以及将它们联合到共同祖先的共祖树内包含的预期世代数时,可以得出另一种推导。这被称为Watterson的𝜃估计器或𝜃W(Yong 2019)。正如我们在共祖中所展示的,n个谱系的预期共祖时间是:

一组n个初始谱系到一个单一祖先的所有共祖时间的总和是:

在每次共祖事件之间的步骤中,有i + 1个谱系可能发生突变。因此,当考虑一段时间内所有谱系可能产生的等位基因数量时,我们乘以i + 1:

我们将树上所有谱系的总时间乘以每代突变率𝜇,得到我们期望在n个DNA序列样本中的等位基因总数,而4N是一个常数,所以我们可以将其放在求和之外

其中S是序列集合中SNP的数量。这可以重新排列以从SNP的数量估计𝜃W=4N𝜇:

请注意,Watterson的𝜃估计器需要了解一组谱系的共祖,但这是在1975年发表的,当时还没有发表超过两个谱系的共祖(Kingman 1982)。Tajima's D是平均成对杂合性𝜃估计值与从样本中SNP数量估计的𝜃之间的差异,除以该差异的预期方差的平方根:

而:


这看起来有点乱,但在各种位置反复出现两个不同的n求和,只需要计算一次然后填入。这可以用以下代码计算(平均成对差异和S也可以从数据集中计算,但为了简洁起见,我们在这里省略了)。
Tajima's D是用来评估一个种群中中性突变(即没有自然选择影响的突变)的假设是否成立。它通过比较两个不同的估计器来衡量种群的遗传多样性和种群规模的变化,我们通过R语言实现:
# Calculates Tajima’s D# 平均成对差异,用于估计theta_IS
theta_IS <- 2.8# 数据集中的SNP数量
S <- 16# 采样的等位基因拷贝数
n <- 20# 初始化求和变量
i1_sum <- 0.0# 循环计算i1的和,这是Watterson's theta的一部分
for(i in 2:n-1){i1_sum <- i1_sum + 1/i
}# 计算Watterson's theta,它是基于序列多态性的一个种群规模的估计器
theta_W <- S / i1_sum# 初始化第二个求和变量
i2_sum <- 0.0# 循环计算i2的和,用于后续计算
for(i in 2:n-1){i2_sum <- i2_sum + 1/i^2
}# 计算期望值e1,它是Tajima's D公式中的项
e1 <- ((n+1)/(3*(n-1)) - 1/i1_sum) / i1_sum# 计算期望值e2,它也是Tajima's D公式中的项
e2 <- (2*(n^2+n+3)/(9*n*(n-1)) - (n+2)/(n*i1_sum) + i2_sum/i1_sum^2) / (i1_sum^2 + i2_sum)# 计算Tajima's D值,它衡量的是theta_IS和theta_W之间的标准化差异
(D <- (theta_IS - theta_W) / sqrt(e1*S + e2*S*(S-1)))前三个变量将根据您的数据进行调整。在这个例子中,返回的D = -1.409。大于或小于2的D被认为是显著的;然而,实际的p值是通过模拟确定的。D的正值表示中间频率等位基因过多,这可能是由于人口减少或平衡选择,因为这两种情况都会延长人口历史较老部分的共祖事件时间。在更大的种群中,有更多的祖先可供选择,共祖是一种罕见的事件,并会膨胀𝜃IS,因为相对于𝜃W,较老的谱系在后代中以更高的频率共享。这种负D表示稀有频率等位基因过多(共祖的最近尖端被放大;它们对S和𝜃W的贡献比对平均成对差异的贡献更多,因为它们很稀有),这表明人口扩张、选择性清除或对有害等位基因的低效净化选择。关键是要计算多个位点的D值,并寻找异常值以标记假定选择候选者。人口统计学效应,如人口规模的变化,应该影响基因组中的所有位点,而选择(通常被认为)在其影响上是位点特异性的。还有许多其他的中性检验,如HKA检验(Hudson等人,1987)、McDonald-Kreitman检验(McDonald和Kreitman,1991)、Fay和Wu的H(Fay和Wu,2000)以及dN/dS比率(Yang和Bielawski,2000)。其中许多也利用了物种之间发生的遗传变化,它们都有各自的优点和缺点。
linkage disequilibrium (LD)
群体遗传学的一个独特性质,在进化博弈论等类似领域中并未发现,即不同位点甚至不同染色体上的等位基因可以“链接”(尽管并不总是与经典遗传学中的重组图谱同义),并且比随机预期更频繁地一起遗传。 连锁不平衡(LD)的程度由𝒟量化,不要与Tajima的D混淆。考虑两个位点:一个具有A/a多态性,另一个具有B/b多态性。我们对于跨位点一起遗传的等位基因之间的关联感到好奇。使用概率的乘法规则,我们期望AB单倍型(pAB)的频率是两个等位基因频率pApB的乘积,如果它们是独立遗传的话。这两者之间的差异由𝒟量化,作为连锁不平衡的一种度量。

根据AB单倍型是过量还是不足,𝒟可以是正数或负数(或者如果你从ab单倍型任意计算𝒟,符号会改变)。𝒟也可以从所有单倍型频率计算得出。

为了说明,假设我们有一个包含两个SNP的单倍型频率的小型数据集。一个是A/G多态性,另一个具有C/T等位基因:

让我们关注A-C单倍型。A等位基因的频率是0.57,C等位基因的频率是0.65

遗传漂变、种群结构和强选择是推动𝒟偏离零的力量。在大种群中,预测𝒟随时间呈指数衰减轨迹返回到零,就像在小种群中遗传漂变下的杂合性一样:

其中r是感兴趣的位点对之间预期的重组分数。这可以用来估计单倍型的年龄。最后,即使对于在不同染色体上独立分配的位点,𝒟也需要时间衰减。哈代-温伯格基因型可以在一代中恢复,但过去的事件对LD有持续影响,这可以用来推断更远的过去的过程,如种群中不再存在的种群结构。 当从实际数据集计算𝒟时,双重杂合子是不明确的。假设我们有一个个体的C/T,A/G SNP集合。C等位基因与第二个位置的A还是G等位基因相关联?通常我们不知道。但是,不明确的单倍型频率为我们提供了关于解决双重杂合子可能方式的信息。如果C-G单倍型非常常见,而C-A单倍型很少见,那么这表明C/T,A/G个体可能具有C-G/T-A单倍型。使用这种方法计算𝒟太繁琐,无法手工完成。 幸运的是,这正是EM算法发挥作用的地方。Kalinowski和Hedrick(2001)使用大角羊(Ovis canadensis)数据集(Boyce等人,1997)来估计LD。这个物种很罕见,样本量很小,所以我们需要从可用的数据中获得尽可能多的信息。 以下R代码实现了Kalinowski和Hedrick(2001)给出的方程式。它从猜测相等的单倍型频率和𝒟 = 0开始。然后它更新这个猜测,并迅速达到最大似然解𝒟 ≈0.0779和na-B单倍型频率基本为零。

# 定义各个复合基因型的频率
AABB <- 2 # 两个位点都是纯合子AABB的个体数量
AaBB <- 0 # 一个位点是杂合子,另一个是纯合子AaBB的个体数量
aaBB <- 0 # 一个位点是纯合子aa,另一个是纯合子BB的个体数量
AABb <- 0 # 第一个位点是纯合子AA,第二个位点是杂合子Bb的个体数量
AaBb <- 1 # 两个位点都是杂合子AaBb的个体数量(双杂合子)
aaBb <- 0 # 第一个位点是纯合子aa,第二个位点是杂合子Bb的个体数量
AAbb <- 1 # 第一个位点是纯合子AA,第二个位点是纯合子bb的个体数量
Aabb <- 0 # 第一个位点是杂合子Aa,第二个位点是纯合子bb的个体数量
aabb <- 0 # 两个位点都是纯合子aabb的个体数量# 使用上述输入运行函数‘Dcalc’
Dcalc(AABB, AaBB, aaBB, AABb, AaBb, aaBb, AAbb, Aabb, aabb)
𝒟与用于衡量线性相关性的统计相关系数(皮尔逊)“r”有关。让我们使用ℛ表示相关系数,以避免将其与重组分数r混淆。𝒟2除以所有等位基因频率的乘积等于ℛ^2。


此外,奇怪的是,如果我们将ℛ2乘以采样的染色体总数(如果我们观察n个二倍体个体,通常为2n),那么我们就会得到一个具有一个自由度的𝜒2统计量:

然而,这并不令人惊讶。在如此小的样本量下,即使LD非常强,检测偏差的能力也非常有限。最后,我们希望指出,EM算法是一种“爬山”算法,它找到一个局部最大似然峰值。可能存在其他峰值,可以使用MCMC方法来处理这个问题,并更全面地探索复杂的似然表面。
相关文章:

【基于R语言群体遗传学】-16-中性检验Tajima‘s D及连锁不平衡 linkage disequilibrium (LD)
Tajimas D Test 已经开发了几种中性检验,用于识别模型假设的潜在偏差。在这里,我们将说明一种有影响力的中性检验,即Tajimas D(Tajima 1989)。Tajimas D通过比较数据集中的两个𝜃 4N𝜇估计值来…...

防火墙组网与安全策略实验
实验要求: 实现: 防火墙接口配置: 所有接口均配置为三层接口 由于G1/0/3口下为vlan环境,所以防火墙需要配置子接口 : 交换机划分vlan分开生产区和办公区、配置trunk干道 : 安全策略: 生产区访…...

xmind梳理测试点,根据这些测试点去写测试用例
基本流(冒烟用例必写) 备选流 公共测试点:...

MICCAI 2024 每日一篇论文 纯纯直读 CUTS:用于多粒度无监督医学图像分割的深度学习和拓扑框架
MICCAI 2024 CUTS: A Deep Learning and Topological Framework for Multigranular Unsupervised Medical Image Segmentation CUTS: 用于多粒度无监督医学图像分割的深度学习和拓扑框架 作者 陈璐1*、Matthew Amodio1*、梁博伦.沈2、冯高3、阿曼阿维斯塔4、Sanjay Aneja3,5…...

实验9 存储过程与函数的创建管理实验
一、实验目的: 理解存储过程和函数的概念。掌握创建存储过程和函数的方法。掌握执行存储过程和函数的方法。掌握游标的定义、使用方法。 二、实验内容 1.某超市的食品管理的数据库的Food表,Food表的定义如表所示, Food表的定义…...

计算机网络--tcpdump和iptable设置、内核参数优化策略
tcpdump工具 tcpdump命令: 选项字段: 过滤表达式: 实用命令: TCP三次握手抓包命令: #客户端执行tcpdump 抓取数据包 tcpdump -i etho tcp and host 192.168.12.36 and port 80 -W timeout.pcapnetstat命令 netst…...

Vue3框架搭建2:axios+typescript封装
仓库地址:https://github.com/buguniao5213/LuArch 1、安装axios npm install axios2、创建文件 先创建一个文件夹: ├── src/ │ ├── api/ │ │ ├── index.ts/ #编写axios封装代码 │ │ └── example.ts/ #定义…...

【机器学习】使用决策树分类器预测汽车安全性的研究与分析
文章目录 一、决策树算法简介决策树的结构分类和回归树 (CART)决策树算法术语决策树算法直觉 二、属性选择度量信息增益熵 基尼指数计算分割基尼指数的步骤 三、决策树算法中的过度拟合避免过度拟合的方法 四、导入库和数据可视化探索性数据分析重命名列名查看数据集的总结信息…...

【香橙派 Orange pi AIpro】| 开发板深入使用体验
目录 一. 🦁 写在前面二. 🦁 愉快的安装流程2.1 安装前准备2.2 流程准备2.2.1 烧录镜像2.2.2 开机2.2.3 连网2.2.4 SSH远程连接开发板 2.3 体验 AI 应用样例 三. 🦁 写在最后 一. 🦁 写在前面 大家好,我是狮子呀&…...

初识Laravel(Laravel的项目搭建)
初识Laravel(Laravel的项目搭建) 一、项目简单搭建(laravel)1.首先我们确保使用国内的 Composer 加速镜像([加速原理](https://learnku.com/php/wikis/30594)):2.新建一个名为 Laravel 的项目&a…...

RequestContextHolder多线程获取不到request对象
RequestContextHolder多线程获取不到request对象,调用feign接口时,在Feign中的RequestInterceptor也获取不到HttpServletRequest问题解决方案。 1.RequestContextHolder多线程获取不到request对象 异常信息,报错如下: 2024-07-0…...

打造高效工作与生活质量的完美平衡
在快节奏的编程行业中,保持健康的工作与生活平衡是至关重要的。长时间坐在电脑前、面对紧凑的项目截止日期和频繁的加班文化,很容易导致身心健康问题,如眼睛疲劳、颈部和背部疼痛、压力累积、睡眠障碍乃至慢性疾病。因此,采取积极…...

【零基础】学JS之APIS第四天
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 非常期待和您一起在这个小…...
走进linux
1、为什么要使用linux 稳定性和可靠性: Linux内核以其稳定性而闻名,能够持续运行数月甚至数年而不需要重新启动。这对于服务器来说至关重要,因为它们需要保持长时间的稳定运行,以提供持续的服务 安全性: Linux系统…...

智能家居开发新进展:乐鑫 ESP-ZeroCode 与亚马逊 ACK for Matter 实现集成
日前,乐鑫 ESP-ZeroCode 与亚马逊 Alexa Connect Kit (ACK) for Matter 实现了集成。这对智能家居设备制造商来说是一项重大进展。开发人员无需编写固件或开发移动应用程序,即可轻松设计符合 Matter 标准的产品。不仅如此,开发者还可以在短短…...

本地事务和分布式事务
一、本地事务 1、事务的基本特性 数据库事务的几个基本特性:原子性、一致性、隔离性、持久性。 原子性:一系列的操作整体不可拆分,要么同时成功,要么同时失败。 一致性:数据在事务的前后,业务整体一…...

昇思25天学习打卡营第14天|基于MindNLP的文本解码原理
基于MindNLP的文本解码原理 文本解码 文本解码是自然语言处理中的一个关键步骤,特别是在任务如机器翻译、文本摘要、自动回复生成等领域。解码过程涉及将编码器(如语言模型、翻译模型等)的输出转换为可读的文本序列。以下是一些常见的文本解码方法和原理: 1. 自回归解码:…...
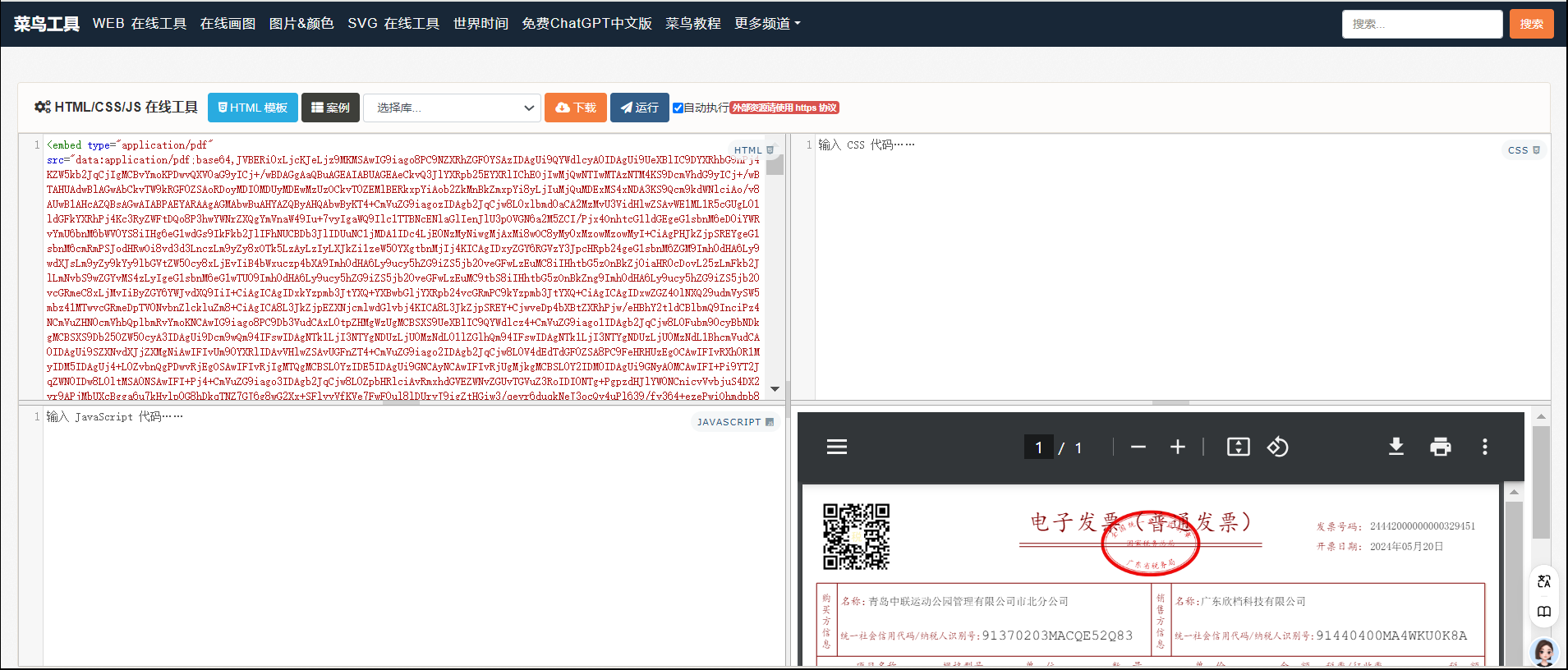
Base64文件流查看下载PDF方法-CSDN
问题描述 数票通等接口返回的PDF类型发票是以Base64文件流的方式返回的,无法直接查看预览PDF发票, 处理方法 使用第三方在线工具:https://www.jyshare.com/front-end/61/ 在Html代码框中粘贴如下代码 <embed type"application/pd…...
基于TCP的在线词典系统(分阶段实现)(阻塞io和多路io复用(select)实现)
1.功能说明 一共四个功能: 注册 登录 查询单词 查询历史记录 单词和解释保存在文件中,单词和解释只占一行, 一行最多300个字节,单词和解释之间至少有一个空格。 2.功能演示 3、分阶段完成各个功能 3.1 完成服务器和客户端的连接 servic…...
设置DepthBufferBits和设置DepthStencilFormat的区别
1)设置DepthBufferBits和设置DepthStencilFormat的区别 2)Unity打包exe后,游戏内拉不起Steam的内购 3)Unity 2022以上Profiler.FlushMemoryCounters耗时要怎么关掉 4)用GoodSky资产包如何实现昼夜播发不同音乐功能 这是…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...

java+webstock
maven依赖 <dependency><groupId>org.java-websocket</groupId><artifactId>Java-WebSocket</artifactId><version>1.3.5</version></dependency><dependency><groupId>org.apache.tomcat.websocket</groupId&…...
