线性代数|机器学习-P22逐步最小化一个函数
文章目录
- 1. 概述
- 2. 泰勒公式
- 3. 雅可比矩阵
- 4. 经典牛顿法
- 4.1 经典牛顿法理论
- 4.2 牛顿迭代法解求方程根
- 4.3 牛顿迭代法解求方程根 Python
- 5. 梯度下降和经典牛顿法
- 5.1 线搜索方法
- 5.2 经典牛顿法
- 6. 凸优化问题
- 6.1 约束问题
- 6.1 凸集组合
Mit麻省理工教授视频如下:逐步最小化一个函数
1. 概述
主要讲的是无约束情况下的最小值问题。涉及到如下:
- 矩阵求导
- 泰勒公式,函数到向量的转换
- 梯度下降
- 牛顿法梯度下降
2. 泰勒公式
我们之前在高等数学中学过关于f(x)的泰勒展开如下:
定义: lim x → a h k ( x ) = 0 \lim\limits_{x\to a}h_k(x)=0 x→alimhk(x)=0
f ( x ) = f ( a ) + f ′ ( a ) ( x − a ) + f ′ ′ ( a ) 2 ! ( x − a ) 2 + ⋯ + f ( k ) ( a ) k ! ( x − a ) k + h k ( x ) ( x − a ) k \begin{equation} f(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2+\cdots+\frac{f^{(k)}(a)}{k!}(x-a)^k+h_k(x)(x-a)^k \end{equation} f(x)=f(a)+f′(a)(x−a)+2!f′′(a)(x−a)2+⋯+k!f(k)(a)(x−a)k+hk(x)(x−a)k
- 那么我们只提取二次项, x + Δ x → x ; x → a x+\Delta x \rightarrow x;x\rightarrow a x+Δx→x;x→a 可得如下:
f ( x + Δ x ) ≈ f ( x ) + f ′ ( x ) Δ x + f ′ ′ ( x ) 2 ! Δ x 2 \begin{equation} f(x+\Delta x)\approx f(x)+f'(x)\Delta x+\frac{f''(x)}{2!}\Delta x^2 \end{equation} f(x+Δx)≈f(x)+f′(x)Δx+2!f′′(x)Δx2 - 上面的公式中x为标量,现在我们需要用到向量 x
- a , b a,b a,b均为1维列向量,S为对称矩阵时,我们可得得到如下:
a T b = c , x T S x = d → c , d 均为标量 \begin{equation} a^Tb=c,x^TSx=d\rightarrow c,d均为标量 \end{equation} aTb=c,xTSx=d→c,d均为标量 - 定义如下:
x = [ x 1 x 2 ⋯ x n ] T , f = [ f 1 f 2 ⋯ f n ] T \begin{equation} x=\begin{bmatrix}x_1&x_2&\cdots&x_n\end{bmatrix}^T,f=\begin{bmatrix}f_1&f_2&\cdots&f_n\end{bmatrix}^T \end{equation} x=[x1x2⋯xn]T,f=[f1f2⋯fn]T
f ′ ( x ) = ∇ F = [ ∂ f ∂ x 1 ∂ f ∂ x 1 ⋯ ∂ f ∂ x n ] T → f ′ ( x ) Δ x = ( Δ x ) T ∇ F ( x ) \begin{equation} f'(x)=\nabla F=\begin{bmatrix}\frac{\partial f}{\partial x_1}&\frac{\partial f}{\partial x_1}&\cdots&\frac{\partial f}{\partial x_n}\end{bmatrix}^T \rightarrow f'(x)\Delta x=(\Delta x)^T \nabla F(x) \end{equation} f′(x)=∇F=[∂x1∂f∂x1∂f⋯∂xn∂f]T→f′(x)Δx=(Δx)T∇F(x) - H j k H_{jk} Hjk为
hessian matrix具有对称性
f ′ ′ ( x ) = H j k = ∂ 2 F ∂ x j ⋅ ∂ x k → f ′ ′ ( x ) 2 ! Δ x 2 = 1 2 ( Δ x ) T H j k ( Δ x ) \begin{equation} f''(x)=H_{jk}=\frac{\partial^2F}{\partial x_j\cdot \partial x_k}\rightarrow \frac{f''(x)}{2!}\Delta x^2=\frac{1}{2}(\Delta x)^T H_{jk}(\Delta x) \end{equation} f′′(x)=Hjk=∂xj⋅∂xk∂2F→2!f′′(x)Δx2=21(Δx)THjk(Δx) - 整理上述公式可得:
F ( x + Δ x ) ≈ F ( x ) + ( Δ x ) T ∇ F ( x ) + 1 2 ( Δ x ) T H j k ( Δ x ) \begin{equation} F(x+\Delta x)\approx F(x)+(\Delta x)^T \nabla F(x)+\frac{1}{2}(\Delta x)^T H_{jk}(\Delta x) \end{equation} F(x+Δx)≈F(x)+(Δx)T∇F(x)+21(Δx)THjk(Δx)
3. 雅可比矩阵
假设有一个m维度向量函数 f ( x ) = [ f 1 ( x ) f 2 ( x ) ⋯ f m ( x ) ] T f(x)=\begin{bmatrix}f_1(x)&f_2(x)&\cdots f_m(x)\end{bmatrix}^T f(x)=[f1(x)f2(x)⋯fm(x)]T[列向量],其中
x = [ x 1 x 2 ⋯ x n ] T x=\begin{bmatrix}x_1&x_2&\cdots&x_n\end{bmatrix}^T x=[x1x2⋯xn]T是一个n维输入向量,雅可比矩阵J是一个 m × n m\times n m×n的矩阵,其元素由函数的偏导数组成:雅可比矩阵第i行第j列表示的是 f i ( x ) f_i(x) fi(x)对 x i x_i xi的偏导
J i j = ∂ f i ( x ) ∂ x j \begin{equation} J_{ij}=\frac{\partial f_i(x)}{\partial x_j} \end{equation} Jij=∂xj∂fi(x)
-
本质上就是函数值 f i ( x ) f_i(x) fi(x)对 x i x_i xi的每个元素求导:
-
第一步假设 f i ( x ) f_i(x) fi(x)是常数, ∂ f i ( x ) ∂ X \frac{\partial f_i(x)}{\partial X} ∂X∂fi(x)为分子布局,遵循标量不变,向量拉伸原则
-
XY拉伸术,分子布局,
X横向拉,Y纵向拉,可得如下:
∂ f i ( x ) ∂ X = [ ∂ f i ( x ) ∂ x 1 ∂ f i ( x ) ∂ x 2 ⋯ ∂ f i ( x ) ∂ x n ] \begin{equation} \frac{\partial f_i(x)}{\partial X}= \begin{bmatrix} \frac{\partial f_i(x)}{\partial x_1}& \frac{\partial f_i(x)}{\partial x_2}& \cdots& \frac{\partial f_i(x)}{\partial x_n} \end{bmatrix} \end{equation} ∂X∂fi(x)=[∂x1∂fi(x)∂x2∂fi(x)⋯∂xn∂fi(x)] -
第二步假设 f ( x ) f(x) f(x)为向量, ∂ f ( x ) ∂ X \frac{\partial f(x)}{\partial X} ∂X∂f(x)为分子布局,遵循标量不变,向量拉伸原则
-
XY拉伸术,分子布局,
X横向拉,Y 纵向拉,可得如下:
J = [ ∂ f 1 ( x ) ∂ x 1 ∂ f 1 ( x ) ∂ x 2 ⋯ ∂ f 1 ( x ) ∂ x n ∂ f 2 ( x ) ∂ x 1 ∂ f 2 ( x ) ∂ x 2 ⋯ ∂ f 2 ( x ) ∂ x n ⋮ ⋮ ⋯ ⋮ ∂ f m ( x ) ∂ x 1 ∂ f m ( x ) ∂ x 2 ⋯ ∂ f m ( x ) ∂ x n ] \begin{equation} \mathrm{J}= \begin{bmatrix} \frac{\partial f_1(x)}{\partial x_1}&\frac{\partial f_1(x)}{\partial x_2}&\cdots&\frac{\partial f_1(x)}{\partial x_n}\\\\ \frac{\partial f_2(x)}{\partial x_1}&\frac{\partial f_2(x)}{\partial x_2}&\cdots&\frac{\partial f_2(x)}{\partial x_n} \\\\ \vdots&\vdots&\cdots&\vdots\\\\\ \frac{\partial f_m(x)}{\partial x_1}&\frac{\partial f_m(x)}{\partial x_2}&\cdots& \frac{\partial f_m(x)}{\partial x_n} \end{bmatrix} \end{equation} J= ∂x1∂f1(x)∂x1∂f2(x)⋮ ∂x1∂fm(x)∂x2∂f1(x)∂x2∂f2(x)⋮∂x2∂fm(x)⋯⋯⋯⋯∂xn∂f1(x)∂xn∂f2(x)⋮∂xn∂fm(x) -
泰勒公式1阶展开可得:
f ( x + Δ x ) = f ( x ) + f ′ ( x ) Δ x \begin{equation} f(x+\Delta x)=f(x)+f'(x)\Delta x \end{equation} f(x+Δx)=f(x)+f′(x)Δx -
转换成雅可比矩阵可得:
f ( x + Δ x ) = f ( x ) + J j k Δ x ; J j k = ∂ f j ( x ) ∂ x k \begin{equation} f(x+\Delta x)=f(x)+\mathrm{J}_{jk}\Delta x;\mathrm{J}_{jk}=\frac{\partial f_j(x)}{\partial x_k} \end{equation} f(x+Δx)=f(x)+JjkΔx;Jjk=∂xk∂fj(x)
4. 经典牛顿法
4.1 经典牛顿法理论
我们已经知道了函数的二阶泰勒展开表示如下:
F ( x + Δ x ) ≈ F ( x ) + ( Δ x ) T ∇ F ( x ) + 1 2 ( Δ x ) T H j k ( Δ x ) \begin{equation} F(x+\Delta x)\approx F(x)+(\Delta x)^T \nabla F(x)+\frac{1}{2}(\Delta x)^T H_{jk}(\Delta x) \end{equation} F(x+Δx)≈F(x)+(Δx)T∇F(x)+21(Δx)THjk(Δx)
- 一般如果在 x ∗ x^* x∗处取得最小值,那么其导数为0;现在我们求导可得:
d F ( x ) d Δ x = 0 ; ( Δ x ) T ∇ F ( x ) d Δ x = ∇ F ( x ) ; d 1 2 ( Δ x ) T H j k ( Δ x ) d Δ x = H j k Δ x ; \begin{equation} \frac{\mathrm{d}F(x)}{\mathrm{d}\Delta x}=0;\frac{(\Delta x)^T \nabla F(x)}{\mathrm{d}\Delta x}=\nabla F(x);\frac{\mathrm{d}\frac{1}{2}(\Delta x)^T H_{jk}(\Delta x)}{\mathrm{d}\Delta x}=H_{jk}\Delta x; \end{equation} dΔxdF(x)=0;dΔx(Δx)T∇F(x)=∇F(x);dΔxd21(Δx)THjk(Δx)=HjkΔx;
d F ( x + Δ x ) d Δ x = 0 + ∇ F ( x ) + H j k Δ x = 0 \begin{equation} \frac{\mathrm{d}F(x+\Delta x)}{\mathrm{d}\Delta x}=0+\nabla F(x)+H_{jk}\Delta x=0 \end{equation} dΔxdF(x+Δx)=0+∇F(x)+HjkΔx=0 - 当 H j k = J j k H_{jk}=\mathrm{J}_{jk} Hjk=Jjk可逆时, Δ x = x k + 1 − x k \Delta x=x_{k+1}-x_k Δx=xk+1−xk可得:
− [ H j k ] − 1 ∇ F ( x ) = x k + 1 − x k → x k + 1 = x k − [ J j k ] − 1 ∇ F ( x ) \begin{equation} -[H_{jk}]^{-1}\nabla F(x)=x_{k+1}-x_k\rightarrow x_{k+1}=x_k-[\mathrm{J}_{jk}]^{-1}\nabla F(x) \end{equation} −[Hjk]−1∇F(x)=xk+1−xk→xk+1=xk−[Jjk]−1∇F(x) - 我们定义 ∇ F ( x ) = f ( x k ) \nabla F(x)=f(x_k) ∇F(x)=f(xk), J j k = J x k \mathrm{J}_{jk}=\mathrm{J}_{x_k} Jjk=Jxk
x k + 1 = x k − [ J x k ] − 1 f ( x k ) \begin{equation} x_{k+1}=x_k-[\mathrm{J}_{x_k}]^{-1}f(x_k) \end{equation} xk+1=xk−[Jxk]−1f(xk)
4.2 牛顿迭代法解求方程根
- 已知: f ( x ) = x 2 − 9 = 0 f(x)=x^2-9=0 f(x)=x2−9=0,用牛顿迭代的方法求解方程的根
- 根据迭代公式可得: f ′ ( x ) = J x k = 2 x , f ( x k ) = x k 2 − 9 f'(x)=\mathrm{J}_{x_k}=2x,f(x_k)=x_k^2-9 f′(x)=Jxk=2x,f(xk)=xk2−9
x k + 1 = x k − [ J x k ] − 1 f ( x k ) → x k + 1 = x k − f ( x k ) J x k \begin{equation} x_{k+1}=x_k-[\mathrm{J}_{x_k}]^{-1}f(x_k)\rightarrow x_{k+1}=x_k-\frac{f(x_k)}{\mathrm{J}_{x_k}} \end{equation} xk+1=xk−[Jxk]−1f(xk)→xk+1=xk−Jxkf(xk) - 整理可得:
x k + 1 = x k − x k 2 − 9 2 x k = 1 2 x k + 9 2 x k \begin{equation} x_{k+1}=x_k-\frac{x_k^2-9}{2x_k}=\frac{1}{2}x_k+\frac{9}{2x_k} \end{equation} xk+1=xk−2xkxk2−9=21xk+2xk9 - 收敛依据:
判断新的近似值 x k + 1 x_{k+1} xk+1与当前值 x k x_k xk之间的差距是否小于某个值 ϵ = 1 0 − 10 \epsilon=10^{-10} ϵ=10−10,如果小于该值则认为收敛,否则继续迭代。 - 我们先设置初始值 x 0 = 2 x_0=2 x0=2可得 x 1 x_1 x1:
x 1 = 1 2 x 0 + 9 2 x 0 = 3.25 ; \begin{equation} x_{1}=\frac{1}{2}x_0+\frac{9}{2x_0}=3.25; \end{equation} x1=21x0+2x09=3.25; - 继续迭代得 x 2 x_2 x2
x 2 = 1 2 x 1 + 9 2 x 1 = 3.0096153846153846 ; \begin{equation} x_{2}=\frac{1}{2}x_1+\frac{9}{2x_1}=3.0096153846153846; \end{equation} x2=21x1+2x19=3.0096153846153846; - 继续迭代得 x 3 x_3 x3
x 3 = 1 2 x 2 + 9 2 x 2 = 3.000015360039322 ; \begin{equation} x_{3}=\frac{1}{2}x_2+\frac{9}{2x_2}=3.000015360039322; \end{equation} x3=21x2+2x29=3.000015360039322; - 继续迭代得 x 4 x_4 x4
x 4 = 1 2 x 3 + 9 2 x 3 = 3.0000000000393214 ; \begin{equation} x_{4}=\frac{1}{2}x_3+\frac{9}{2x_3}=3.0000000000393214; \end{equation} x4=21x3+2x39=3.0000000000393214; - 可得 x 2 − 9 = 0 x^2-9=0 x2−9=0的解为 x 1 ∗ = 3 x_1^*=3 x1∗=3,同理初始化为 x 0 = − 2 x_0=-2 x0=−2 可得 x 2 ∗ = − 3 x_2^*=-3 x2∗=−3
4.3 牛顿迭代法解求方程根 Python
- 代码:
Python代码如下:
def newton_raphson(f, f_prime, x0, tol=1e-10, max_iter=100):x = x0for i in range(max_iter):fx = f(x)fpx = f_prime(x)# Newton-Raphson iterationx_new = x - fx / fpxprint(f"Iteration {i + 1}: x = {x_new}")if abs(x_new - x) < tol:return x_newx = x_newraise ValueError("Newton-Raphson method did not converge")# Define the function and its first derivative
f = lambda x: x ** 2 - 9
f_prime = lambda x: 2 * x# Initial guesses
initial_guesses = [2, -2]# Find the roots
for x0 in initial_guesses:root = newton_raphson(f, f_prime, x0)print(f"The root starting from {x0} is: {root}")
- 运行结果:
Iteration 1: x = 3.25
Iteration 2: x = 3.0096153846153846
Iteration 3: x = 3.000015360039322
Iteration 4: x = 3.0000000000393214
Iteration 5: x = 3.0
The root starting from 2 is: 3.0
Iteration 1: x = -3.25
Iteration 2: x = -3.0096153846153846
Iteration 3: x = -3.000015360039322
Iteration 4: x = -3.0000000000393214
Iteration 5: x = -3.0
The root starting from -2 is: -3.0
5. 梯度下降和经典牛顿法
对于无约束问题的梯度下降,我们一般有两种方法:
5.1 线搜索方法
运用泰勒一阶信息,迭代方向为负梯度方向:
- 迭代方程:
x k + 1 = x k + α k p k \begin{equation} x_{k+1}=x_k +\alpha_k p_k \end{equation} xk+1=xk+αkpk - 方向 p k p_k pk:负梯度方向 − ∇ F -\nabla F −∇F
- 步长: α k = s k \alpha_k=s_k αk=sk,深度学习中叫学习率
- 更新后的方程如下:
x k + 1 = x k − s k ∇ F \begin{equation} x_{k+1}=x_k -s_k \nabla F \end{equation} xk+1=xk−sk∇F
5.2 经典牛顿法
运用泰勒二阶信息,迭代方向为牛顿方向:迭代步长为 α 1 = 1 \alpha_1=1 α1=1
- 迭代方程为,
hessian matrix->H j k H_{jk} Hjk可逆:
x k + 1 = x k − [ H j k ] − 1 ∇ F ( x ) \begin{equation} x_{k+1}=x_k-[H_{jk}]^{-1}\nabla F(x) \end{equation} xk+1=xk−[Hjk]−1∇F(x) - 经典牛顿法为二次性收敛,速度非常快,具体分析请参考如下博客
[优化算法]经典牛顿法
6. 凸优化问题
6.1 约束问题
我们定义凸函数为 f ( x ) f(x) f(x),凸集为 K \mathrm{K} K,我们的目的是为了求得凸函数 f ( x ) f(x) f(x)的最小值
min x ∈ K f ( x ) , K : A x = b \begin{equation} \min\limits_{x\in K} f(x), \mathrm{K}:Ax=b \end{equation} x∈Kminf(x),K:Ax=b
- f ( x ) f(x) f(x)表示的是所有在碗内部上的和碗内表面上的点
- 求的是在碗内表面的上的最小值,碗的形状就是约束条件 A x = b Ax=b Ax=b

6.1 凸集组合
- 如果 x 1 , x 2 x_1,x_2 x1,x2均在凸集里面,则由 x 1 , x 2 x_1,x_2 x1,x2组成的直线L在凸集里面

- 如果 x 1 , x 2 x_1,x_2 x1,x2分别在不同的凸集里面,则由 x 1 , x 2 x_1,x_2 x1,x2组成的直线L不在凸集里面

- 小结:合并图集里面组合的直线不在凸集里面。
- 如果 x 1 , x 2 x_1,x_2 x1,x2都在不同的凸集里面的交集里面,则由 x 1 , x 2 x_1,x_2 x1,x2组成的直线L在凸集中

- 假设我们有两个凸函数 F 1 ( x ) , F 2 ( x ) F_1(x),F_2(x) F1(x),F2(x),我们定义如下:
min ( x ) = min [ F 1 ( x ) , F 2 ( x ) ] ; max ( x ) = max [ F 1 ( x ) , F 2 ( x ) ] ; \begin{equation} \min(x)=\min[F_1(x),F_2(x)];\max(x)=\max[F_1(x),F_2(x)]; \end{equation} min(x)=min[F1(x),F2(x)];max(x)=max[F1(x),F2(x)]; - 如果两个凸集相交,那么相交的凸集最大值,最小值如下:
min ( x ) = min [ F 1 ( x ) , F 2 ( x ) ] − > 非凸; max ( x ) = max [ F 1 ( x ) , F 2 ( x ) ] − > 凸 ; \begin{equation} \min(x)=\min[F_1(x),F_2(x)]-> 非凸;\max(x)=\max[F_1(x),F_2(x)]->凸; \end{equation} min(x)=min[F1(x),F2(x)]−>非凸;max(x)=max[F1(x),F2(x)]−>凸; - 凸函数判断
d 2 f ( x ) d x 2 ≥ 0 \begin{equation} \frac{\mathrm{d}^2f(x)}{\mathrm{d}x^2}\ge 0 \end{equation} dx2d2f(x)≥0
相关文章:

线性代数|机器学习-P22逐步最小化一个函数
文章目录 1. 概述2. 泰勒公式3. 雅可比矩阵4. 经典牛顿法4.1 经典牛顿法理论4.2 牛顿迭代法解求方程根4.3 牛顿迭代法解求方程根 Python 5. 梯度下降和经典牛顿法5.1 线搜索方法5.2 经典牛顿法 6. 凸优化问题6.1 约束问题6.1 凸集组合 Mit麻省理工教授视频如下:逐步…...

SpringCloudAlibaba Nacos配置中心与服务发现
目录 1.配置 1.1配置的特点 只读 伴随应用的整个生命周期 多种加载方式 配置需要治理 1.2配置中心 2.Nacos简介 2.1特性 服务发现与服务健康检查 动态配置管理 动态DNS服务 服务和元数据管理 3.服务发现 1.配置 应用程序在启动和运行的时候往往需要读取一些配置信…...

.NET 一款获取内网共享机器的工具
01阅读须知 此文所提供的信息只为网络安全人员对自己所负责的网站、服务器等(包括但不限于)进行检测或维护参考,未经授权请勿利用文章中的技术资料对任何计算机系统进行入侵操作。利用此文所提供的信息而造成的直接或间接后果和损失…...
备考美国数学竞赛AMC8和AMC10:吃透1850道真题和知识点(持续)
距离接下来的AMC8、AMC10美国数学竞赛还有几个月的时间,实践证明,做真题,吃透真题和背后的知识点是备考AMC8、AMC10有效的方法之一。 通过做真题,可以帮助孩子找到真实竞赛的感觉,而且更加贴近比赛的内容,…...
旅游景区度假村展示型网站如何建设渠道品牌
景区、度假村、境外旅游几乎每天的人流量都非常高,还包括本地附近游等,对景区及度假村等固定高流量场所,品牌和客户赋能都是需要完善的,尤其是信息展示方面,旅游客户了解前往及查看信息等。 通过雨科平台建设景区度假…...

Python酷库之旅-第三方库Pandas(021)
目录 一、用法精讲 52、pandas.from_dummies函数 52-1、语法 52-2、参数 52-3、功能 52-4、返回值 52-5、说明 52-6、用法 52-6-1、数据准备 52-6-2、代码示例 52-6-3、结果输出 53、pandas.factorize函数 53-1、语法 53-2、参数 53-3、功能 53-4、返回值 53-…...

jvm 06 补充 OOM 和具体工具使用
1.OOM 是什么 OOM,全称“Out Of Memory”,翻译成中文就是“内存用完了”,来源于java.lang.OutOfMemoryError。看下关于的官方说明: Thrown when the Java Virtual Machine cannot allocate an object because it is out of memor…...

使用机器学习 最近邻算法(Nearest Neighbors)进行点云分析 (scikit-learn Open3D numpy)
使用 NearestNeighbors 进行点云分析 在数据分析和机器学习领域,最近邻算法(Nearest Neighbors)是一种常用的非参数方法。它广泛应用于分类、回归和聚类分析等任务。下面将介绍如何使用 scikit-learn 库中的 NearestNeighbors 类来进行点云数…...

安装jenkins最新版本初始化配置及使用JDK1.8构建项目详细讲解
导读 1.安装1.1.相关网址1.2.准备环境1.3.下载安装 2. 配置jenkins2.1.安装插件2.2.配置全局工具2.3.系统配置 3. 使用3.1.配置job3.2.构建 提示:如果只想看如何使用jdk1.8构建项目,直接看3.1即可。 1.安装 1.1.相关网址 Jenkins官网:https…...

微软子公司Xandr遭隐私诉讼,或面临巨额罚款
近日,欧洲隐私权倡导组织noyb对微软子公司Xandr提起了诉讼,指控其透明度不足,侵犯了欧盟公民的数据访问权。据指控,Xandr的行为涉嫌违反《通用数据保护条例》(GFPR),因其处理信息并创建用于微目…...

【VRP】基于常春藤算法IVY求解带时间窗的车辆路径问题TWVRP,最短距离附Matlab代码
% VRP - 基于IVY算法的TWVRP最短距离求解 % 数据准备 % 假设有一组客户点的坐标和对应的时间窗信息 % 假设数据已经存储在 coordinates、timeWindows 和 demands 变量中 % 参数设置 numCustomers size(coordinates, 1); % 客户点数量 vehicleCapacity 100; % 车辆容量 numV…...

常用软件的docker compose安装
简介 Docker Compose 是 Docker 的一个工具,用于定义和管理多容器 Docker 应用。通过使用一个单独的 YAML 文件,您可以定义应用所需的所有服务,然后使用一个简单的命令来启动和运行这些服务。Docker Compose 非常适合于微服务架构或任何需要…...

Excel第28享:如何新建一个Excel表格
一、背景需求 小姑电话说:要新建一个表格,并实现将几个单元格进行合并的需求。 二、解决方案 1、在电脑桌面上空白地方,点击鼠标右键,在下拉的功能框中选择“XLS工作表”或“XLSX工作表”都可以,如下图所示。 之后&…...

计算机网络知识汇总
OSI七层模型 七层模型一般指开放系统互连参考模型,开放系统互连参考模型 (Open System Interconnect 简称OSI),OSI参考模型是具有7个层次的框架,自底向上的7个层次分别是物理层、数据链路层、网络层、传输层、会话层、…...
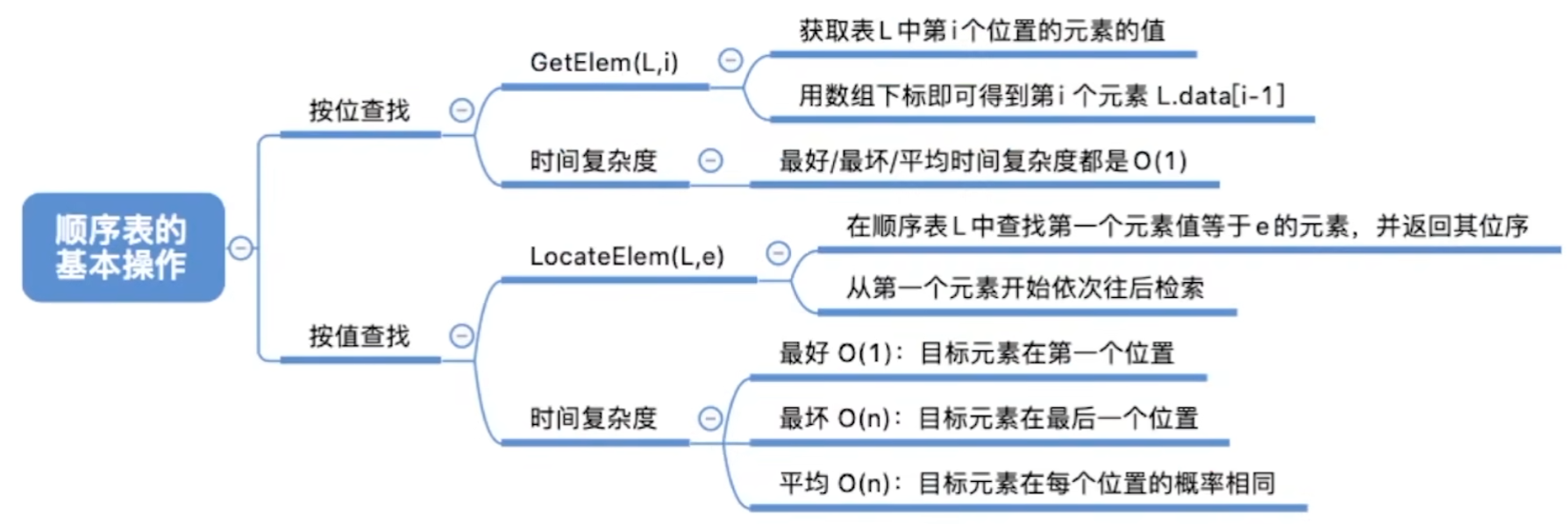
数据结构——考研笔记(二)线性表的定义和线性表之顺序表
文章目录 二、线性表2.1 定义、基本操作2.1.1 知识总览2.1.2 线性表的定义2.1.3 线性表的基本操作2.1.4 知识回顾与重要考点 2.2 顺序表2.2.1 知识总览2.2.2 顺序表的定义2.2.3 顺序表的实现——静态分配2.2.4 顺序表的实现——动态分配2.2.5 知识回顾与重要考点2.2.6 顺序表的…...

quota使用
一、检查系统是否支持 grep CONFIG_QUOTA /boot/config* CONFIG_QUOTAy CONFIG_QUOTA_NETLINK_INTERFACEy # CONFIG_QUOTA_DEBUG is not set CONFIG_QUOTA_TREEy CONFIG_QUOTACTLy CONFIG_QUOTACTL_COMPATy二、安装 yum install -y quota三、配置 3.1 创建磁盘 格式一定要 …...

解决fidder小黑怪倒出JMeter文件缺失域名、请求头
解决fidder小黑怪倒出JMeter文件缺失域名、请求头 1、目录结构: 2、代码 coding:utf-8 Software:PyCharm Time:2024/7/10 14:02 Author:Dr.zxyimport zipfile import os import xml.etree.ElementTree as ET import re#定义信息头 headers_to_extract [Host, Conn…...

智慧城市的神经网络:Transformer模型在智能城市构建中的应用
智慧城市的神经网络:Transformer模型在智能城市构建中的应用 随着城市化的快速发展,智能城市的概念应运而生,旨在通过先进的信息技术提升城市管理效率和居民生活质量。Transformer模型,作为人工智能领域的一颗新星,其…...

产品经理-研发流程-敏捷开发-迭代-需求评审及产品规划(15)
敏捷开发是以用户的需求进化为核心,采用迭代、循序渐进的方法进行软件开发。 通俗来说,敏捷开发是一个软件开发流程,是一个采用了迭代方法的开发流程 简单来说,迭代就是把一个大产品拆分出一些最小的实现单位。完成不同的迭代就最…...

Ansible 安装及使用说明
方案1. 直接下载 源码包到本地后安装 ansible 下载地址:https://releases.ansible.com/ansible/ ansible社区: https://github.com/ansible/ansible 下载地址:GitHub - ansible/ansible at v2.9.0 方案2. 以腾讯的yum源说明:腾讯云文档…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...

使用 uv 工具快速部署并管理 vLLM 推理环境
uv:现代 Python 项目管理的高效助手 uv:Rust 驱动的 Python 包管理新时代 在部署大语言模型(LLM)推理服务时,vLLM 是一个备受关注的方案,具备高吞吐、低延迟和对 OpenAI API 的良好兼容性。为了提高部署效…...
