蓝桥冲刺31天之316
如果生活突然向你发难
躲不过那就迎面而战
所谓无坚不摧
是能享受最好的,也能承受最坏的
大不了逢山开路,遇水搭桥
若你决定灿烂,山无遮,海无拦
A:特殊日期
问题描述
对于一个日期,我们可以计算出年份的各个数位上的数字之和,也可以分别计算月和日的各位数字之和。请问从 1900 年 1 月 1 日至 9999 年 12 月 31日,总共有多少天,年份的数位数字之和等于月的数位数字之和加日的数位数字之和。
例如,2022 年 11 月 13 日满足要求,因为 2+0+2+2=(1+1)+(1+3) 。
请提交满足条件的日期的总数量。
题解思路:通过 time包直接进行读取判断即可
参考代码:
import java.time.*;
public class Main {public static void main(String[] args) {LocalDate date = LocalDate.of(1900,1,1);int count=0;while(true){if(date.getYear()==9999&&date.getMonth().getValue()==12&&date.getDayOfMonth()==31) break;int x1 = date.getYear()%10;int x2 = date.getYear()/10%10;int x3 = date.getYear()/100%10;int x4 = date.getYear()/1000;int y1 = date.getMonth().getValue()%10;int y2 = date.getMonth().getValue()/10;int y3 = date.getDayOfMonth()%10;int y4 = date.getDayOfMonth()/10;if((x1+x2+x3+x4)==(y1+y2+y3+y4)) count++;date = date.plusDays(1);}System.out.println(count);}
}
B:重合次数
问题描述
在同一天中, 从上午 6 点 13 分 22 秒到下午 14 点 36 分 20 秒, 钟表上的 分针和秒针一共重合了多少次?
注意时针、分针、秒针都围绕中心敳匀速运动。
题解思路:
误区在于一个小时重合60次,实际上每个小时只会重合59次,从早上6点到14点总共8小时,59*8=472,然后从13分22秒到35分22秒多有22次重合,而35分22秒多到36分20秒没有重合,因此结果:59*8*22=494
答案:
494
C:左移右移
问题描述
小蓝有一个长度为 N 的数组, 初始时从左到右依次是 1,2,3,…N。
之后小蓝对这个数组进行了 M 次操作, 每次操作可能是以下 2 种之一:
左移 x, 即把 x 移动到最左边。
右移 x, 即把 x 移动到最右边。
请你回答经过 M 次操作之后, 数组从左到右每个数是多少?
输入格式
第一行包含 2 个整数, N 和 M 。
以下 M 行每行一个操作, 其中 “L x "表示左移 x,"R x "表示右移 x 。
输出格式
输出 N 个数, 代表操作后的数组。
样例输入
5 3 L 3 L 2 R 1样例输出
2 3 4 5 1样例说明
样例中的数组变化如下:
[1,2,3,4,5]→[3,1,2,4,5]→[2,3,1,4,5]→[2,3,4,5,1][1,2,3,4,5]→[3,1,2,4,5]→[2,3,1,4,5]→[2,3,4,5,1]
评测用例规模与约定
对于 50% 的评测用例, 1≤N,M≤10000
对于 100% 的评测用例, 1≤N,M≤200000,1≤x≤N
题解思路:
我们可以知道的结论:最后移动的数一定在两边,且不会因为前面移动过这个数而对这个数产生影响,而前面的数会因为后面的数移动而改变位置,那么我们是否可以逆向判断,固定 两边的数,其他没有移动过的数按照从左到右顺序排列
那我们需要用到哪些东西?
一个长M的数组,去存储移动信息
一个长N+1的boolean数组,去判断1--N是否移动使用
一个长为N的数组,去存储最终结果并用于输出
参考代码:
import java.util.*;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n=sc.nextInt();int m=sc.nextInt();char []s=new char[m];//存储输入的字符int []arr=new int[m];//存储输入的值boolean []bl=new boolean[n+1];//判断是否用于交换int []jg=new int[n];//存储结果for(int i=0;i<m;i++){//输入s[i]=sc.next().charAt(0);arr[i]=sc.nextInt();}int l=0,r=n-1;for(int i=m-1;i>=0;i--){//逆序去判断每一个数if(s[i]=='L'&&bl[arr[i]]==false){//说明这个数在最左边且未被使用jg[l]=arr[i];bl[arr[i]]=true;l++;//左端点+1,下一个移到最左边的话会在这个数的右边}else if(s[i]=='R'&&bl[arr[i]]==false){//说明这个数在最右边且未被使用jg[r]=arr[i];bl[arr[i]]=true;r--;//右端点-1,,下一个移到最右边的话会在这个数的左边}}for(int i=1;i<=n;i++){//去判断所有数字中没有使用过的if(bl[i]==false){//进行存储jg[l]=i;l++;}}for(int i=0;i<n;i++) System.out.print(jg[i]+" ");//输出}
}D:近似gcd
问题描述
小蓝有一个长度为 nn 的数组 A=(a1,a2,⋯ ,an), 数组的子数组被定义为从 原数组中选出连续的一个或多个元素组成的数组。数组的最大公约数指的是数 组中所有元素的最大公约数。如果最多更改数组中的一个元素之后, 数组的最 大公约数为 g, 那么称 g 为这个数组的近似 GCD。一个数组的近似 GCD 可能 有多种取值。
具体的, 判断 g 是否为一个子数组的近似 GCD 如下:
如果这个子数组的最大公约数就是 g, 那么说明 g 是其近似 GCD。
在修改这个子数组中的一个元素之后 (可以改成想要的任何值), 子数 组的最大公约数为 g, 那么说明 g 是这个子数组的近似 GCD。
小蓝想知道, 数组 A 有多少个长度大于等于 2 的子数组满足近似 GCD 的 值为 g 。
输入格式
输入的第一行包含两个整数 n,g, 用一个空格分隔, 分别表示数组 A 的长 度和 g 的值。
第二行包含 nn 个整数 a1,a2,⋯ ,an, 相邻两个整数之间用一个空格分隔。
输出格式
输出一行包含一个整数表示数组 A 有多少个长度大于等于 2 的子数组的近 似 GCD 的值为 g
样例输入
5 3 1 3 6 4 10样例输出
5样例说明
满足条件的子数组有 5 个:
[1,3][1,3] : 将 1 修改为 3 后, 这个子数组的最大公约数为 3 , 满足条件。
[1,3,6][1,3,6] : 将 1 修改为 3 后, 这个子数组的最大公约数为 3 , 满足条件。
[3,6]:这个子数组的最大公约数就是 3 , 满足条件。
[3,6,4][3,6,4] : 将 4 修改为 3 后, 这个子数组的最大公约数为 3 , 满足条件。
[6,4][6,4] : 将 4 修改为 3 后, 这个子数组的最大公约数为 3 , 满足条件。
评测用例规模与约定
对于 20%20% 的评测用例, 2≤n≤10^2 ;
对于 40%40% 的评测用例, 2≤n≤10^3;
对于所有评测用例, 2≤n≤10^5,1≤g,ai≤10^9。
题解思路:
对于每一个数,我们先去判断这个数是否为g的倍数,我们将非g倍数的数提取出来存放对应下标,在[L,R]区间中,按照2/3/4.....R-L个数的数组一共存在:(1+2+...+R-L-1)*(R-L-1)/2个
而在区间内最多只能存在一个数不是g的倍数
我们按照每一个提取的数为节点,进行与前后数的组合统计,得到公式如下:
((arr[r]-arr[r-2]-2)+(arr[r]-arr[r-1]-1))*(arr[r-1]-arr[r-2])/2
最终特判所有数都是g的倍数与只有一个数是g的倍数的情况即可
PS: 不知道怎么说比较清楚,通过等差公式推出来的,可以看代码试试
参考代码:
import java.util.*;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);long n=sc.nextLong();int m=sc.nextInt();long []arr=new long[100010];int l=1;//输入和提取非m倍数的数for(long i=1;i<=n;i++){int a=sc.nextInt();if(a%m!=0){arr[l]=i;l++;}}arr[l]=n+1;//最有端点设置一个long sum=0;for(int i=2;i<l;i++){//公式代入sum+=((arr[i]-arr[i-2]-2)+(arr[i]-arr[i-1]-1))*(arr[i-1]-arr[i-2])/2;}if(l<=2){//只有一个非m倍数的数或者全是m倍数的数System.out.println(n*(n-1)/2);return;}//最右端点的特殊求和sum+=(arr[l]-arr[l-2]-1)*(arr[l]-arr[l-2]-2)/2;System.out.println(sum);}
}相关文章:

蓝桥冲刺31天之316
如果生活突然向你发难 躲不过那就迎面而战 所谓无坚不摧 是能享受最好的,也能承受最坏的 大不了逢山开路,遇水搭桥 若你决定灿烂,山无遮,海无拦 A:特殊日期 问题描述 对于一个日期,我们可以计算出年份的各个…...
说一个通俗易懂的PLC工程师岗位要求
你到了一家新的单位,人家接了一套新的设备,在了解设备工艺流程之后,你就能决定用什么电气元件,至少95%以上电气原件不论你用过没用过都有把握拍板使用,剩下5%,3%你可以先买来做实验,这次不能用&…...

今年还能学java么?
“Java很卷”、“大家不要再卷Java了”,经常听到同学这样抱怨。但同时,Java的高薪也在吸引越来越多的同学。不少同学开始疑惑:既然Java这么卷,还值得我入行吗? 首先先给你吃一颗定心丸:现在选择Java依然有…...

ajax学习1
不刷新页面的情况下,向服务端发送请求,异步的js和XMLajax不是新的编程语言,只是把现有标准组合到一起使用的新方式...
)
一题多解-八数码(万字长文)
16 张炜皓 (ζ͡顾念̶) LV 5 1 周前 在做这道题前,先来认识一下deque双端队列 C STL 中的双端队列 题目连接 使用前需要先引入 头文件。 #include; STL 中对 deque 的定义 // clang-format off template< class T, class Allocator std::allocator class d…...
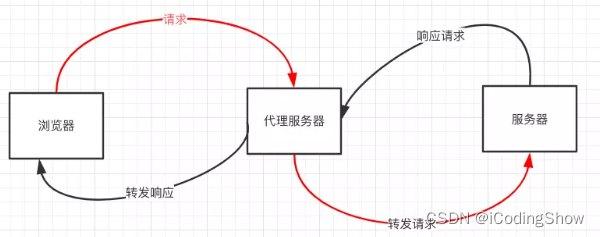
九种跨域方式实现原理(完整版)
前言 前后端数据交互经常会碰到请求跨域,什么是跨域,以及有哪几种跨域方式,这是本文要探讨的内容。 一、什么是跨域? 1.什么是同源策略及其限制内容? 同源策略是一种约定,它是浏览器最核心也最基本的安…...
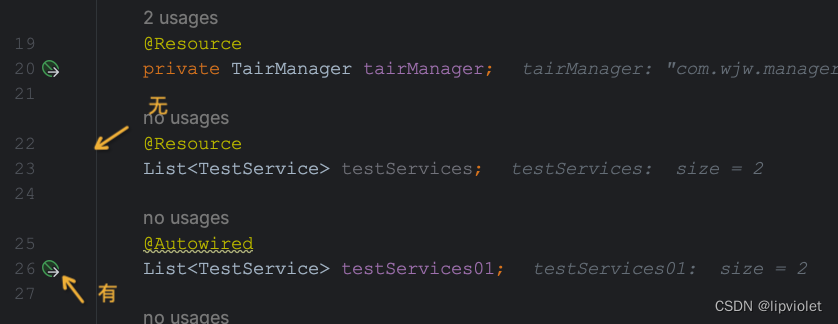
fighting
目录Mysqlgroup by和 distinct哪个性能好java觉得Optional类怎么样isEmpty和isBlank的用法区别使用大对象时需要注意什么内存溢出和内存泄漏的区别及详解SpringResource和Autowired的起源既生“Resource”,何生“Autowired”使用Autowired时为什么Idea会曝出黄色警告…...

网络安全日志监控管理
内部安全的重要性 无论大小,每个拥有IT基础设施的组织都容易发生内部安全攻击。您的损失等同于黑客的收益:访问机密数据、滥用检索到的信息、系统崩溃,以及其他等等。专注于网络外部的入侵是明智的,但同时,内部安全也…...
线程池的使用:如何写出高效的多线程程序?
目录1.线程池的使用2.编写高效的多线程程序Java提供了Executor框架来支持线程池的实现,通过Executor框架,可以快速地创建和管理线程池,从而更加方便地编写多线程程序。 1.线程池的使用 在使用线程池时,需要注意以下几点ÿ…...
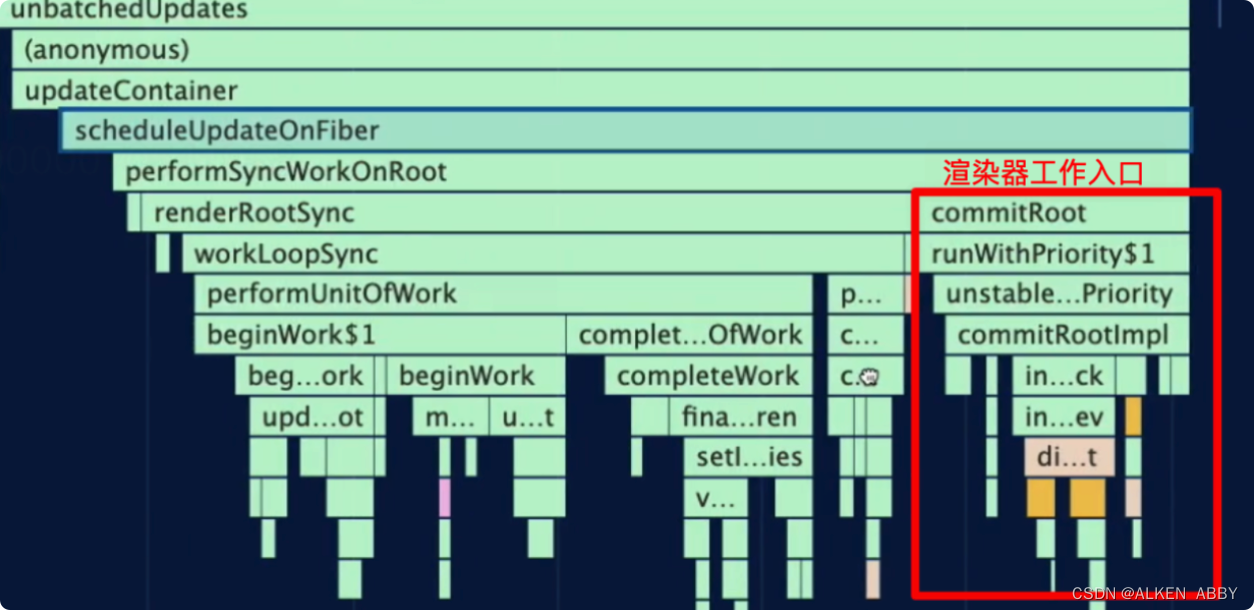
React 架构流程概览
React 架构流程概览 文章目录React 架构流程概览启动React项目流程分析各部分解析调度器协调器渲染器总结启动React项目 启动项目,并打开 Performance 面板 流程分析 首先找到入口函数 整个 render 下面的调用栈就是首屏渲染要执行的流程。 render 过程大致分为…...

【Linux】进程管理之kill、killall、pkill
一、kill 命令 Linux 中的 kill 命令用来终止指定的进程的运行,是 Linux 下进程管理的常用命令。通常,终止一个前台进程可以使用 CtrlC 键,但是,对于一个后台进程就须用 kill 命令来终止,那就需要先使用 ps、pidof、ps…...
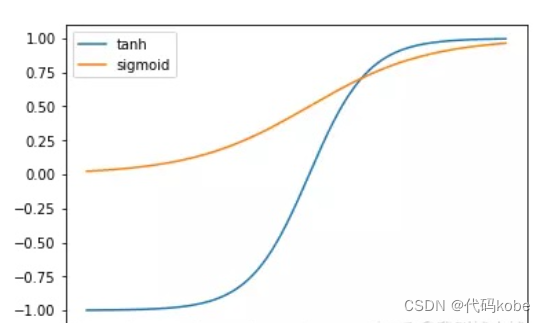
LSTM从入门到精通(形象的图解,详细的代码和注释,完美的数学推导过程)
先附上这篇文章的一个思维导图什么是RNN按照八股文来说:RNN实际上就是一个带有记忆的时间序列的预测模型RNN的细胞结构图如下:softmax激活函数只是我举的一个例子,实际上得到y<t>也可以通过其他的激活函数得到其中a<t-1>代表t-1时…...

19.特殊工具与技术
文章目录特殊工具与技术19.1控制内存分配19.1.1重载new和deleteoperator new接口和operator delete接口malloc函数与free函数19.1.2定位new表达式显式的析构函数调用19.2运行时类型识别(run-time type identification, RTTI)19.2.1dynamic_cast运算符指针类型的dynamic_cast引用…...

518. 零钱兑换 II ——【Leetcode每日一题】
518. 零钱兑换 II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 3…...

django DRF请求访问频率限制
Django REST framework(DRF)提供了一个throttle_classes属性,可以用于限制API的访问频率。它可以防止恶意用户发送大量请求以消耗服务器资源。使用throttle_classes属性,需要在settings.py中配置REST_FRAMEWORK:REST_F…...

二分查找创新性总结
LeetCode题目 704.二分查找35.搜索插入位置69.x 的平方根367.有效的完全平方数34.在排序数组中查找元素的第一个和最后一个位置 二分查找适用范围 可随机访问的数据结构数据已经有序要查找的值只有一个 上述的前四题都可直接使用二分查找,第五题要求查找上限和下限&…...

Java Web 实战 13 - 多线程进阶之 synchronized 原理以及 JUC 问题
文章目录一 . synchronized 原理1.1 synchronized 使用的锁策略1.2 synchronized 是怎样自适应的? (锁膨胀 / 升级 的过程)1.3 synchronized 其他的优化操作锁消除锁粗化1.4 常见面试题二 . JUC (java.util.concurrent)2.1 Callable 接口2.2 ReentrantLock2.3 原子类2.4 线程池…...
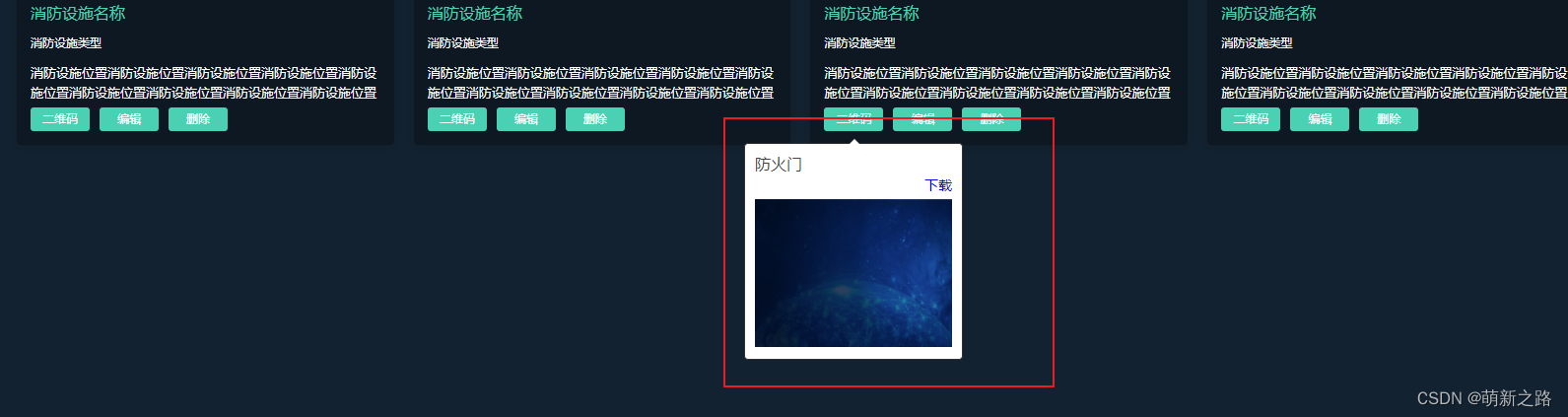
【解决】elementui ——tooltip提示在循环中点击一个,同时显示多个的问题!
同时显示多个tooltip——效果图: 点击第一个二维码把循环el-card中所有的tooltip都触发了 解决后效果图: 只显示点击的当前tooltip 解决办法: 通过循环item中定义字段,进行控制tooltip显示隐藏 代码: 页面代码&am…...
SpringBoot-核心技术篇
技术掌握导图 六个大标题↓ 配置文件web开发数据访问单元测试指标指控原理解析 配置文件 1.文件类型 1.1、properties 同以前的properties用法 1.2、yaml 1.2.1、简介 YAML是 “YAML Aint Markup Language”(YAML不是一种标记语言)的递归缩写。在…...

2023还有人不知道kubernetes?| 初步理解kubernetes
文章目录Kubernetes(K8s)一、Openstack&VM1、**认识虚拟化****1.1**、什么是虚拟化**1.2、虚拟化分类**2、OpenStack与KVM、VMWare2.1、OpenStack2.2、KVM2.3、VMWare二、容器&编排技术1、容器发展史1.1、Chroot1.2、FreeBSD Jails1.3、Solaris Zones1.4、LXC1.5、Dock…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
