概率论原理精解【3】
文章目录
- 向量值
- 向量值函数导数
- 对称矩阵
- 定义
- 性质
- 例子
- 应用
- 向量值理论基础
- 定义
- 性质
- 应用
- 示例
- 向量值函数的导数
- 定义
- 性质
- 应用
向量值
向量值函数导数
- D n ⊂ R n , 向量值函数 f : D n → R m D^n \subset R^n,向量值函数f:D^n\rightarrow R^m Dn⊂Rn,向量值函数f:Dn→Rm
1. 向量值函数 f = ( f 1 , f 2 , . . . , f m ) T ,称 f i 为坐标函数 2. 复合函数 f i : π i ∘ f , i = 1 , 2 , . . . , m π i : R m → R , x → x i 为坐标映射。 3. f i : D n → R 的导数定义为: f ˙ i ( x ) = d d x f i ( x ) = ( ∂ ∂ x 1 f i ( x ) , ∂ ∂ x 2 f i ( x ) , . . . . ∂ ∂ x n f i ( x ) ) 4. f ˙ ( x ) = ∂ ∂ x f ( x ) = ( d d x f 1 ( x ) d d x f 2 ( x ) . . . d d x f m ( x ) ) = ( ∂ ∂ x 1 f 1 ( x ) ∂ ∂ x 2 f 1 ( x ) . . . ∂ ∂ x n f 1 ( x ) ∂ ∂ x 1 f 2 ( x ) ∂ ∂ x 2 f 2 ( x ) . . . ∂ ∂ x n f 2 ( x ) . . . . . . . . . ∂ ∂ x 1 f m ( x ) ∂ ∂ x 2 f m ( x ) . . . ∂ ∂ x n f m ( x ) ) m × n 1.向量值函数f=(f_1,f_2,...,f_m)^T,称f_i为坐标函数 \\2.复合函数f_i:\pi_i \circ f,i=1,2,...,m \\\pi_i:R^m\rightarrow R,x \rightarrow x_i为坐标映射。 \\3.f_i:D^n \rightarrow R的导数定义为: \\\dot f_i(x)=\frac d {dx}f_i(x)=(\frac {\partial} {\partial x_1}f_i(x),\frac {\partial} {\partial x_2}f_i(x),....\frac {\partial} {\partial x_n}f_i(x)) \\4.\dot f(x)=\frac {\partial} {\partial x}f(x)=\begin{pmatrix} \frac d {dx}f_1(x) \\ \frac d {dx}f_2(x)\\ ...\\ \frac d {dx}f_m(x) \end{pmatrix} \\=\begin{pmatrix} \frac {\partial} {\partial x_1}f_1(x)& \frac {\partial} {\partial x_2}f_1(x)& ...&\frac {\partial} {\partial x_n}f_1(x) \\ \frac {\partial} {\partial x_1}f_2(x)& \frac {\partial} {\partial x_2}f_2(x)& ...&\frac {\partial} {\partial x_n}f_2(x) \\ ... & ...&...\\ \frac {\partial} {\partial x_1}f_m(x)& \frac {\partial} {\partial x_2}f_m(x)& ...&\frac {\partial} {\partial x_n}f_m(x) \\ \end{pmatrix}_{m \times n} 1.向量值函数f=(f1,f2,...,fm)T,称fi为坐标函数2.复合函数fi:πi∘f,i=1,2,...,mπi:Rm→R,x→xi为坐标映射。3.fi:Dn→R的导数定义为:f˙i(x)=dxdfi(x)=(∂x1∂fi(x),∂x2∂fi(x),....∂xn∂fi(x))4.f˙(x)=∂x∂f(x)= dxdf1(x)dxdf2(x)...dxdfm(x) = ∂x1∂f1(x)∂x1∂f2(x)...∂x1∂fm(x)∂x2∂f1(x)∂x2∂f2(x)...∂x2∂fm(x)............∂xn∂f1(x)∂xn∂f2(x)∂xn∂fm(x) m×n - 向量值函数 f : R 3 → R 2 向量值函数f:R^3\rightarrow R^2 向量值函数f:R3→R2为 f ( x , y , z ) = f(x,y,z)= f(x,y,z)=
( 7 x 5 − 3 y 3 c o s z 8 x 7 + e y z ) m = 2 , n = 3 , f 的导数 = ( 35 x 4 9 y 2 c o s z 3 y 3 s i n z 56 x 6 e y z e y ) 2 × 3 \begin{pmatrix} \\7x^5-3y^3cosz \\8x^7+e^yz \end{pmatrix} \\m=2,n=3,f的导数= \\\begin{pmatrix} \\35x^4 & 9y^2cosz & 3y^3sinz \\56x^6 & e^yz & e^y \end{pmatrix}_{2\times 3} 7x5−3y3cosz8x7+eyz m=2,n=3,f的导数= 35x456x69y2coszeyz3y3sinzey 2×3 - a = ( a 1 , a 2 . . . , a n ) T 是常数向量, x = ( x 1 , x 2 , . . . x n ) T 是变量 a=(a_1,a_2...,a_n)^T是常数向量,x=(x_1,x_2,...x_n)^T是变量 a=(a1,a2...,an)T是常数向量,x=(x1,x2,...xn)T是变量
∂ ( a T x ) ∂ ( x ) = ∂ ( x T a ) ∂ ( x ) = a T \frac {\partial(a^Tx)} {\partial(x)}=\frac {\partial(x^Ta)} {\partial(x)}=a^T ∂(x)∂(aTx)=∂(x)∂(xTa)=aT - 若 A = ( a i j ) m × n 是常数矩阵 , x = ( x 1 , x 2 , . . . x n ) T 是变量,则 若A=(a_{ij})_{m \times n}是常数矩阵,x=(x_1,x_2,...x_n)^T是变量,则 若A=(aij)m×n是常数矩阵,x=(x1,x2,...xn)T是变量,则
∂ ( A x ) ∂ ( x ) = A \frac {\partial(Ax)} {\partial(x)}=A ∂(x)∂(Ax)=A - 若 A = ( a i j ) m × n 是常数矩阵 ( 不要求对称 ) , x = ( x 1 , x 2 , . . . x n ) T 是变量,则 若A=(a_{ij})_{m \times n}是常数矩阵(不要求对称),x=(x_1,x_2,...x_n)^T是变量,则 若A=(aij)m×n是常数矩阵(不要求对称),x=(x1,x2,...xn)T是变量,则
∂ ( x T A x ) ∂ ( x ) = x T ( A + A T ) , A 对称时, ∂ ( x T A x ) ∂ x = 2 x T A \frac {\partial(x^TAx)} {\partial(x)} = x^T(A+A^T),A对称时,\frac {\partial(x^TAx)} {\partial x}=2x^TA ∂(x)∂(xTAx)=xT(A+AT),A对称时,∂x∂(xTAx)=2xTA
对称矩阵
对称矩阵(Symmetric Matrix)是一个方阵,其满足矩阵的转置等于它本身,即对于任意的矩阵元素 a i j a_{ij} aij,都有 a i j = a j i a_{ij} = a_{ji} aij=aji。这意味着矩阵沿主对角线是对称的。在数学中,特别是线性代数、矩阵理论和统计学等领域,对称矩阵有着广泛的应用。
定义
设 A A A是一个 n × n n \times n n×n的矩阵,如果满足条件 A T = A A^T = A AT=A(其中 A T A^T AT是 A A A的转置矩阵),则称 A A A为对称矩阵。
性质
- 对角线上的元素都是实数:因为 a i i = a i i T = a i i a_{ii} = a_{ii}^T = a_{ii} aii=aiiT=aii,所以对角线上的元素不变。
- 关于主对角线对称: a i j = a j i a_{ij} = a_{ji} aij=aji,即矩阵的任意元素关于主对角线对称。
- 特征值都是实数:对称矩阵的所有特征值都是实数,且其特征向量可以选择为正交的。
- 可以对角化:对称矩阵可以通过相似变换对角化,即存在一个可逆矩阵 P P P,使得 P − 1 A P P^{-1}AP P−1AP是对角矩阵。
- 在二次型中的应用:对称矩阵在二次型理论中起着重要作用,因为任意二次型都可以表示为一个对称矩阵的二次形式。
例子
A = ( 2 3 4 3 0 5 4 5 6 ) A = \begin{pmatrix} 2 & 3 & 4 \\ 3 & 0 & 5 \\ 4 & 5 & 6 \end{pmatrix} A= 234305456
由于 A T = A A^T = A AT=A(可以通过验证每个元素 a i j = a j i a_{ij} = a_{ji} aij=aji来确认),所以 A A A是一个对称矩阵。
应用
对称矩阵在物理、工程、统计学等领域有着广泛的应用。例如,在物理学中,许多物理量(如应力、应变、电势等)的矩阵表示都是对称的;在统计学中,协方差矩阵就是一个对称矩阵,它描述了多个随机变量之间的线性关系。此外,在数值分析和机器学习等领域,对称矩阵的对角化也是常用的技术之一。
向量值理论基础
向量值函数是数学中的一个重要概念,特别是在多元微积分和向量分析中。它是指一个函数,其输出是一个向量,而不是一个单一的标量值。这种函数通常用于描述在多维空间中随时间或其他变量变化的量。
定义
向量值函数可以定义为:
r ( t ) = ⟨ x ( t ) , y ( t ) , z ( t ) ⟩ \mathbf{r}(t) = \langle x(t), y(t), z(t) \rangle r(t)=⟨x(t),y(t),z(t)⟩
其中, t t t 是一个实数变量(通常是时间),而 x ( t ) x(t) x(t)、 y ( t ) y(t) y(t) 和 z ( t ) z(t) z(t) 是关于 t t t 的三个实值函数,分别表示向量在三维空间中的 x x x、 y y y 和 z z z 分量。
性质
向量值函数具有一些重要的性质,包括:
-
可加性:如果 r ( t ) \mathbf{r}(t) r(t) 和 s ( t ) \mathbf{s}(t) s(t) 是两个向量值函数,则它们的和 r ( t ) + s ( t ) \mathbf{r}(t) + \mathbf{s}(t) r(t)+s(t) 也是一个向量值函数,其分量为对应分量之和。
-
数乘:对于任意实数 k k k, k r ( t ) k\mathbf{r}(t) kr(t) 也是一个向量值函数,其分量为原函数分量的 k k k 倍。
-
导数:向量值函数关于其变量的导数(如果存在)是一个新的向量值函数,其分量为原函数各分量关于该变量的导数。
-
积分:向量值函数也可以进行积分运算,得到的结果是一个向量值函数(定积分)或一个向量场(不定积分或曲线积分)。
应用
向量值函数在物理学、工程学、计算机科学和经济学等多个领域都有广泛的应用。以下是一些例子:
-
物理学:在物理学中,向量值函数常用于描述质点的位置、速度、加速度等物理量。例如,质点的位置随时间变化的函数就是一个向量值函数。
-
工程学:在工程学中,向量值函数可用于描述机械系统的位移、速度、加速度以及力、力矩等物理量。此外,它们还用于分析电路中的电流和电压等。
-
计算机科学:在计算机图形学和动画中,向量值函数用于描述物体的运动轨迹、旋转和变形等。
-
经济学:在经济学中,向量值函数可用于描述多个经济变量的变化关系,如供需关系、价格变动等。
示例
考虑一个简单的例子,一个质点在三维空间中沿直线运动,其位置随时间变化的函数为:
r ( t ) = ⟨ t , 2 t , 3 t ⟩ \mathbf{r}(t) = \langle t, 2t, 3t \rangle r(t)=⟨t,2t,3t⟩
这个向量值函数表示质点在 x x x、 y y y 和 z z z 方向上的位移分别是 t t t、 2 t 2t 2t 和 3 t 3t 3t。对这个函数求导,我们得到质点的速度向量:
r ′ ( t ) = ⟨ 1 , 2 , 3 ⟩ \mathbf{r}^{\prime}(t) = \langle 1, 2, 3 \rangle r′(t)=⟨1,2,3⟩
这表明质点在每个方向上的速度都是恒定的,且速度向量与 t t t 无关。
向量值函数的导数
也称为向量函数的导数或向量场的导数,是多元微积分中的一个重要概念。它描述了向量值函数如何随着其输入变量的变化而变化。
定义
设有一个向量值函数 r ( t ) = ⟨ x ( t ) , y ( t ) , z ( t ) ⟩ \mathbf{r}(t) = \langle x(t), y(t), z(t) \rangle r(t)=⟨x(t),y(t),z(t)⟩,其中 t t t 是实数变量, x ( t ) x(t) x(t)、 y ( t ) y(t) y(t) 和 z ( t ) z(t) z(t) 是关于 t t t 的实值函数。向量值函数 r ( t ) \mathbf{r}(t) r(t) 的导数定义为:
r ′ ( t ) = lim Δ t → 0 r ( t + Δ t ) − r ( t ) Δ t \mathbf{r}^{\prime}(t) = \lim_{{\Delta t \to 0}} \frac{\mathbf{r}(t + \Delta t) - \mathbf{r}(t)}{\Delta t} r′(t)=Δt→0limΔtr(t+Δt)−r(t)
这可以进一步展开为:
r ′ ( t ) = lim Δ t → 0 ⟨ x ( t + Δ t ) , y ( t + Δ t ) , z ( t + Δ t ) ⟩ − ⟨ x ( t ) , y ( t ) , z ( t ) ⟩ Δ t \mathbf{r}^{\prime}(t) = \lim_{{\Delta t \to 0}} \frac{\langle x(t + \Delta t), y(t + \Delta t), z(t + \Delta t) \rangle - \langle x(t), y(t), z(t) \rangle}{\Delta t} r′(t)=Δt→0limΔt⟨x(t+Δt),y(t+Δt),z(t+Δt)⟩−⟨x(t),y(t),z(t)⟩
= lim Δ t → 0 ⟨ x ( t + Δ t ) − x ( t ) Δ t , y ( t + Δ t ) − y ( t ) Δ t , z ( t + Δ t ) − z ( t ) Δ t ⟩ = \lim_{{\Delta t \to 0}} \left\langle \frac{x(t + \Delta t) - x(t)}{\Delta t}, \frac{y(t + \Delta t) - y(t)}{\Delta t}, \frac{z(t + \Delta t) - z(t)}{\Delta t} \right\rangle =Δt→0lim⟨Δtx(t+Δt)−x(t),Δty(t+Δt)−y(t),Δtz(t+Δt)−z(t)⟩
= ⟨ x ′ ( t ) , y ′ ( t ) , z ′ ( t ) ⟩ = \langle x^{\prime}(t), y^{\prime}(t), z^{\prime}(t) \rangle =⟨x′(t),y′(t),z′(t)⟩
其中 x ′ ( t ) x^{\prime}(t) x′(t)、 y ′ ( t ) y^{\prime}(t) y′(t) 和 z ′ ( t ) z^{\prime}(t) z′(t) 分别是 x ( t ) x(t) x(t)、 y ( t ) y(t) y(t) 和 z ( t ) z(t) z(t) 关于 t t t 的导数。
性质
-
线性性:如果 r ( t ) \mathbf{r}(t) r(t) 和 s ( t ) \mathbf{s}(t) s(t) 是向量值函数,且 a a a 和 b b b 是常数,则
( a r + b s ) ′ ( t ) = a r ′ ( t ) + b s ′ ( t ) (a\mathbf{r} + b\mathbf{s})^{\prime}(t) = a\mathbf{r}^{\prime}(t) + b\mathbf{s}^{\prime}(t) (ar+bs)′(t)=ar′(t)+bs′(t)
-
乘积法则(对于标量函数和向量值函数的乘积):如果 f ( t ) f(t) f(t) 是标量函数, r ( t ) \mathbf{r}(t) r(t) 是向量值函数,则
( f r ) ′ ( t ) = f ′ ( t ) r ( t ) + f ( t ) r ′ ( t ) (f\mathbf{r})^{\prime}(t) = f^{\prime}(t)\mathbf{r}(t) + f(t)\mathbf{r}^{\prime}(t) (fr)′(t)=f′(t)r(t)+f(t)r′(t)
注意,这里的乘积是标量与向量的乘积,结果仍为向量。
-
链式法则:如果 u = g ( t ) u = g(t) u=g(t) 是一个可微函数,且 r ( u ) \mathbf{r}(u) r(u) 是一个向量值函数,则复合函数 r ( g ( t ) ) \mathbf{r}(g(t)) r(g(t)) 的导数为
d d t r ( g ( t ) ) = r ′ ( g ( t ) ) ⋅ g ′ ( t ) \frac{d}{dt}\mathbf{r}(g(t)) = \mathbf{r}^{\prime}(g(t)) \cdot g^{\prime}(t) dtdr(g(t))=r′(g(t))⋅g′(t)
其中 r ′ ( g ( t ) ) \mathbf{r}^{\prime}(g(t)) r′(g(t)) 是向量值函数在 g ( t ) g(t) g(t) 处的导数,而 g ′ ( t ) g^{\prime}(t) g′(t) 是 g ( t ) g(t) g(t) 的导数,这里的乘法是标量与向量的乘法。
应用
向量值函数的导数在物理学、工程学以及许多其他领域都有广泛应用。例如,在物理学中,它可以用来描述质点的速度(位置向量的导数)和加速度(速度向量的导数)。在工程学中,它可以用来分析曲线的切线方向和曲率等几何特性。
相关文章:

概率论原理精解【3】
文章目录 向量值向量值函数导数对称矩阵定义性质例子应用 向量值理论基础定义性质应用示例 向量值函数的导数定义性质应用 向量值 向量值函数导数 D n ⊂ R n , 向量值函数 f : D n → R m D^n \subset R^n,向量值函数f:D^n\rightarrow R^m Dn⊂Rn,向量值函数f:Dn→Rm 1. 向量…...
)
[C/C++入门][循环]14、计算2的幂(2的n次方)
计算2的幂(即2的n次方)非常经典。你懂几种方法呢?很多人只会一种,我们来分析一下。 可以通过多种方式实现: 1、最简单的方法之一是使用位运算符<<,它本质上是在二进制表示下对2进行左移操作&#x…...

RPC与服务的注册发现
文章目录 1. 什么是远程过程调用(RPC)?2. RPC的流程3. RPC实践4. RPC与REST的区别4.1 RPC与REST的相似之处4.2 RPC与REST的架构原则4.3 RPC与REST的主要区别 5. RPC与服务发现5.1 以zookeeper为服务注册中心5.2 以etcd为服务注册中心 6. 小结参考 1. 什么是远程过程调用(RPC)?…...
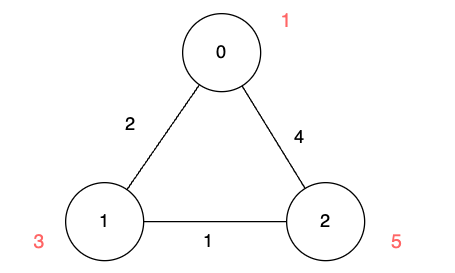
3112. 访问消失节点的最少时间 Medium
给你一个二维数组 edges 表示一个 n 个点的无向图,其中 edges[i] [ui, vi, lengthi] 表示节点 ui 和节点 vi 之间有一条需要 lengthi 单位时间通过的无向边。 同时给你一个数组 disappear ,其中 disappear[i] 表示节点 i 从图中消失的时间点࿰…...

FastAPI 学习之路(五十二)WebSockets(八)接受/发送json格式消息
前面我们发送的大多数都是text类型的消息,对于text消息来说,后端处理出来要麻烦的多,那么我们可以不可以传递json格式的数据,对于前后端来说都比较友好,答案是肯定的,我们需要做下处理。 首先,…...

Go语言并发编程-案例_3
案例 并发目录大小统计 业务逻辑 统计目录的文件数量和大小(或其他信息)。示例输出: // 某个目录:2637 files 1149.87 MB 实现思路 给定一个或多个目录,并发的统计每个目录的size,最后累加到一起。 当…...

pikachu之跨站脚本攻击(x‘s‘s)
1get型 输入a看一下 接着输入<a> 发现<>没有被过滤当做标签处理了 尝试在表单提交的框里面,输入xss语句 尝试输入<script>alert(1)</script> 发现有长度限制 因为这里是get请求 get请求的特点是:传参是在url中的 所以我们可以在…...

Qt模型/视图架构——委托(delegate)
一、为什么需要委托 模型(model)用来数据存储,视图(view)用来展示数据。因此,模型/视图架构是一种将数据存储和界面展示分离的编程方法。具体如下图所示: 由图可知,模型向视图提供数…...

python3.11SSL: SSLV3_ALERT_HANDSHAKE_FAILURE
参考:python request包 版本不兼容 报错sslv3 alert handshake failure 解决方法-CSDN博客 修改:Python311\Lib\site-packages\urllib3\util\ssl_.py 新版本3.11里默认没有DEFAULT_CIPHERS 补回来: #__imported from 3.6.8 # A secure default. # So…...
[深度学习]基于yolov10+streamlit目标检测演示系统设计
YOLOv10结合Streamlit构建的目标检测系统,不仅极大地增强了实时目标识别的能力,还通过其直观的用户界面实现了对图片、视频乃至摄像头输入的无缝支持。该系统利用YOLOv10的高效检测算法,能够快速准确地识别图像中的多个对象,并标注…...

开源模型应用落地-FastAPI-助力模型交互-进阶篇(三)
一、前言 FastAPI 的高级用法可以为开发人员带来许多好处。它能帮助实现更复杂的路由逻辑和参数处理,使应用程序能够处理各种不同的请求场景,提高应用程序的灵活性和可扩展性。 在数据验证和转换方面,高级用法提供了更精细和准确的控制&#…...

机器人及其相关工科专业课程体系
机器人及其相关工科专业课程体系 前言传统工科专业机械工程自动化/控制工程计算机科学与技术 新兴工科专业智能制造人工智能机器人工程 总结Reference: 前言 机器人工程专业是一个多领域交叉的前沿学科,涉及自然科学、工程技术、社会科学、人文科学等相关学科的理论…...

C#数字医学影像系统(RIS/PACS)源码,Oracle数据库,C/S架构,运行稳定
数字医学影像系统(RIS/PACS)源码,三甲以下的医院都能满足。PACS 系统全套成品源码。 开发技术:C/S架构,C#开发语言,数据库服务器采用Oracle数据库。 医学影像存储与传输系统,融合了医学信息化…...
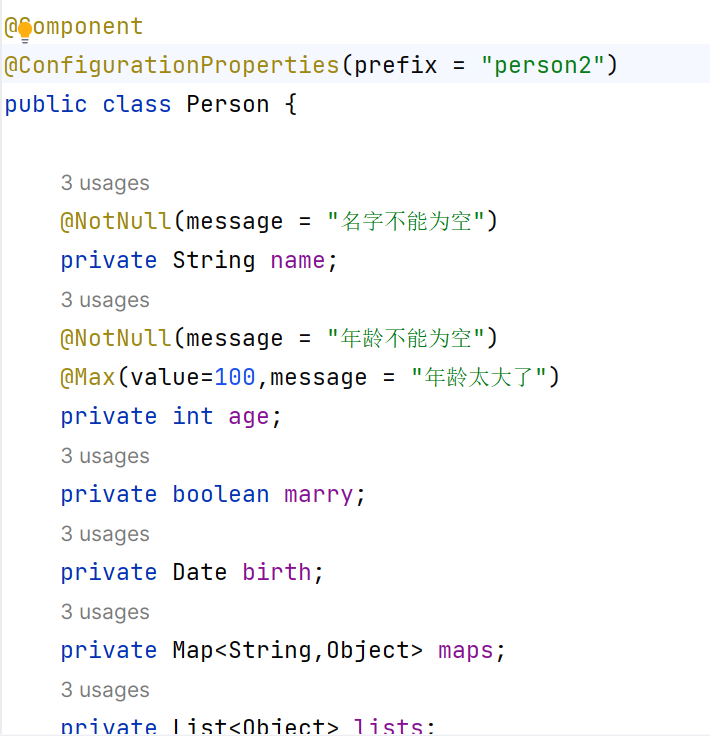
Spring-Boot基础--yaml
目录 Spring-Boot配置文件 注意: YAML简介 YAML基础语法 YAML:数据格式 YAML文件读取配置内容 逐个注入 批量注入 ConfigurationProperties 和value的区别 Spring-Boot配置文件 Spring-Boot中不用编写.xml文件,但是spring-Boot中还是存在.prope…...
C/C++蓝屏整人代码
文章目录 📒程序效果 📒具体步骤 1.隐藏任务栏 2.调整cmd窗口大小 3.调整cmd窗口屏幕颜色 4.完整代码 📒代码详解 🚀欢迎互三👉:程序猿方梓燚 💎💎 🚀关注博主&a…...

【Android安全】Ubuntu 下载、编译 、刷入Android-8.1.0_r1
0. 环境准备 Ubuntu 16.04 LTS(预留至少95GB磁盘空间,实测占94.2GB) Pixel 2 XL 要买欧版的,不要美版的。 欧版能解锁BootLoader、能刷机。 美版IMEI里一般带“v”或者"version",这样不能解锁BootLoader、…...

HBuilder X3.4版本中使用uni-app自定义组件
HBuilder X3.4版本中使用uni-app自定义组件 这是我的小程序页面结构 方式一:导入components 1.创建componets文件,并编写你的组件页面 <template><view class"my-search-container"><!-- 使用 view 组件模拟 input 输入框的样…...

PHP基础语法(一)
一、初步语法 1、PHP代码标记:以 <?php 开始,以 ?> 结束; 2、PHP注释:行注释://(双斜杠)或# 块注释:/* */ 3、PHP语句分隔符: 1)在PHP中&#…...

Python项目打包与依赖管理指南
在Python开发中,python文件需要在安装有python解释器的计算机的电脑上才能运行,但是在工作时,我们需要给客户介绍演示项目功能时并不一定可以条件安装解释器,而且这样做非常不方便。这时候我们可以打包项目,用于给客户…...

矿产资源潜力预测不确定性评价
研究目的: 不确定性评估: 到底什么叫不确定性,简单来说就是某区域内的矿产资源量,并不确定到底有多少,你需要给出一个评估或者分布。 研究方法: 1.以模糊集来表示某些量: 关于什么是模糊集&am…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
