C语言超市管理系统UI界面



以下是部分代码。需要源码的私信
#include<easyx.h>
#include<stdio.h>
#include<stdlib.h>#define width 1280
#define height 840
#define font_w 35 //字体宽度
#define font_h 90 //字体高度typedef struct node
{char name[100];//名字char number[100];//编号char classify[100];//分类int price;//进价int sales;//售价int repertory;//库存int extant;///现存node* nxet;
}Lnode, * Hnode;
Lnode L;//创建头结点//用于历史记录
typedef struct anode
{char name[100];char number[100];char classify[100];int price;int sales;int repertory;int extant;
}ARRnode;ARRnode ArrList[1000];
int count_goods = 0;//全局变量--统计商品的多少int InitList(Lnode& L) //初始化链表
{L.nxet = NULL; //创建一个头结点return 0;
}int history_count = 0;//用于判断是否有历史记录
int history_goods_Lnode(Lnode& L)//将history中的数据读入到链表中
{FILE* fp = fopen("./history.txt", "r");if (!fp){printf("读取history失败\n");return 0;}Lnode* p, * q;p = &L;q = (Lnode*)malloc(sizeof(Lnode));if (!q){printf("q--malloc失败\n");return 0;}while (fscanf(fp, "%s%s%s%d%d%d%d", q->name, q->number, q->classify, &q->price, &q->sales, &q->repertory, &q->extant) != EOF){ history_count++;//记录链表中的数据数p->nxet = q;p = q;q = (Lnode*)malloc(sizeof(Lnode));if (!q){printf("q--malloc失败\n");return 0;}}p->nxet = NULL;printf("history_count=%d\n", history_count);fclose(fp);return 0;
}
相关文章:

C语言超市管理系统UI界面
以下是部分代码。需要源码的私信 #include<easyx.h> #include<stdio.h> #include<stdlib.h>#define width 1280 #define height 840 #define font_w 35 //字体宽度 #define font_h 90 //字体高度typedef struct node {char name[100];//名字char number[1…...

BUUCTF逆向wp [MRCTF2020]Xor
第一步 查壳,该题是32位,无壳。 第二步 跟进main,发现反汇编不了 通过下图我们可以发现一串类似字符串的东西 第三步 我们看一下汇编 我们可以得到这些信息:flag的长度为27(下面是对本条指令cmp edx 27指令的应用…...

Windows版MySQL5.7解压直用(如何卸载更换位置重新安装)
文章目录 停止mysql进程及服务迁移整个mysql文件夹删除data重启计算机重新安装 停止mysql进程及服务 net stop mysql mysqld -remove mysql迁移整个mysql文件夹 删除data 重启计算机 shutdown -r -t 0重新安装 https://blog.csdn.net/xzzteach/article/details/137723185...

详解数据结构之二叉树(堆)
详解数据结构之二叉树(堆) 树 树的概念 树是一个非线性结构的数据结构,它是由 n(n>0)个有限节点组成的一个具有层次关系的集合,它的外观形似一颗倒挂着的树,根朝上,叶朝下,所以称呼为树。每颗子树的根节点有且只…...

Linux----Mplayer音视频库的移植
想要播放视频音乐就得移植相关库到板子上 Mplayer移植需要依赖以下源文件:(从官网获取或者网上) 1、zlib-1.2.3.tar.gz :通用的内存空间的压缩库。 2、libpng-1.2.57.tar.gz :png格式图片的压缩或解压库 3、Jpegsrc.v9b.tar.gz : jpeg格式图片的压…...

STM32测测速---编码电机读取速度的计算
1、首先先了解一下计算的公式 速度计算: 轮胎每转一圈的脉冲数取决于编码器的分辨率,可由下面公式进行计算: PPR是电机的线数 以GA25-370电机为例。 图片来源:第四节:STM32定时器(4.JGA25-370霍尔编码器…...

【已解决】服务器无法联网与更换镜像源
目录 问题描述: 1.修改网卡的 DNS1 和 DNS2 2.修改DNS列表 3.重启网络服务 4.切换镜像源 4.1备份原镜像源 4.2下载阿里云镜像源 4.3替换无法使用的域名 4.4刷新软件包缓存 4.5其他镜像源 5.阿里云镜像源开发者社区说明 6.阿里云DNS网址 7.DNS域名服务器…...

android11 屏蔽usb通过otg转接口外接鼠标设备
硬件平台:QCS6125 软件平台:Android11 需求:Android设备通过接usb转接线连接鼠标功能屏蔽。 考虑到屏蔽的层面可以从两个层面去做,一个是驱动层面不识别,一个就是Android系统层面不识别加载,本篇只讲后者。…...

HAL库源码移植与使用之RTC时钟
实时时钟(Real Time Clock,RTC),本质是一个计数器,计数频率常为秒,专门用来记录时间。 普通定时器无法掉电运行!但RTC可由VBAT备用电源供电,断电不断时 这里讲F1系列的RTC 可以产生三个中断信号ÿ…...

GIT命令学习 一
📑打牌 : da pai ge的个人主页 🌤️个人专栏 : da pai ge的博客专栏 ☁️宝剑锋从磨砺出,梅花香自苦寒来 ☁️运维工程师的职责:监…...

VS+QT 打包可执行文件.exe
切换成release版本,同时更改项目属性中release配置下的各个属性,确保匹配 重新生成解决方案,将生成的.exe复制到一个空白文件夹中 执行: cd D:\QT\5.12.10\msvc2015_64\binwindeployqt C:\Users\DELL\Desktop\serials\MainWind…...
)
Android笔试面试题AI答之Activity(2)
答案仅供参考,大部分为文心一言AI作答 目录 1. 请介绍一下Activity 生命周期?1. 完全生命周期2. 可见生命周期3. 前台生命周期4. 配置更改5. 特殊场景 2. 请介绍一下横竖屏切换时Activity的生命周期变化?1.默认行为(未设置androi…...
 通俗解释)
来自Transformers的双向编码器表示(BERT) 通俗解释
来自Transformers的双向编码器表示(BERT) 目录 1. 从上下文无关到上下文敏感2. 从特定于任务到不可知任务3. BERT:把两个最好的结合起来4. BERT的输入表示5. 掩蔽语言模型(Masked Language Modeling)6. 下一句预测&am…...
)
代码随想录第十六天|贪心算法(2)
目录 LeetCode 134. 加油站 LeetCode 135. 分发糖果 LeetCode 860. 柠檬水找零 LeetCode 406. 根据身高重建队列 LeetCode 452. 用最少数量的箭引爆气球 LeetCode 435. 无重叠区间 LeetCode 763. 划分字母区间 LeetCode 56. 合并区间 LeetCode 738. 单调递增的数字 总…...

花几千上万学习Java,真没必要!(二十二)
1、final关键字: 测试代码1: package finaltest.com;public class FinalBasicDemo {public static void main(String[] args) {// final修饰基本数据类型变量final int number 5;// 尝试修改number的值,这将导致编译错误// number 10; // …...

在RK3568上如何烧录MAC?
这里我们用RKDevInfoWriteTool 1.1.4版本 下载地址:https://pan.baidu.com/s/1Y5uNhkyn7D_CjdT98GrlWA?pwdhm30 提 取 码:hm30 烧录过程: 1. 解压RKDevInfoWriteTool_Setup_V1.4_210527.7z 进入解压目录,双击运行RKDevInfo…...
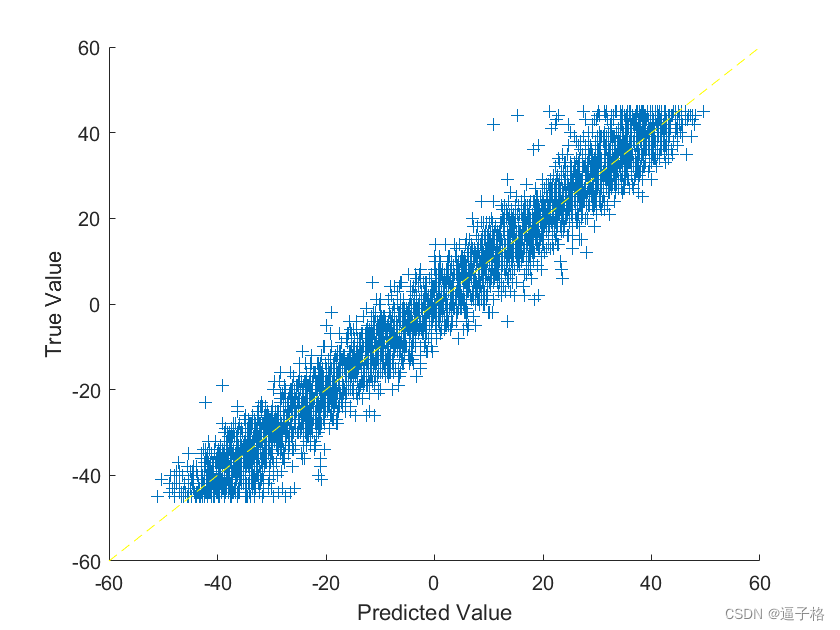
1.30、基于卷积神经网络的手写数字旋转角度预测(matlab)
1、卷积神经网络的手写数字旋转角度预测原理及流程 基于卷积神经网络的手写数字旋转角度预测是一个常见的计算机视觉问题。在这种情况下,我们可以通过构建一个卷积神经网络(Convolutional Neural Network,CNN)来实现该任务。以下…...

Windows如何使用Python的sphinx
在Windows上使用Python的Sphinx进行文档渲染和呈现,可以遵循以下步骤进行操作: 安装Python:首先,确保你的Windows系统上已经安装了Python。你可以从Python的官方网站下载并安装适合你系统(32位或64位&…...

C++ STL nth_element 用法
一:功能 将一个序列分为两组,前一组元素都小于*nth,后一组元素都大于*nth, 并且确保第 nth 个位置就是排序之后所处的位置。即该位置的元素是该序列中第nth小的数。 二:用法 #include <vector> #include <a…...

【PostgreSQL教程】PostgreSQL 选择数据库
博主介绍:✌全网粉丝20W+,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物联网、机器学习等设计与开发。 感兴趣的可…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...
