【线性代数】矩阵变换
一些特殊的矩阵
一,对角矩阵
1,什么是对角矩阵

表示将矩阵进行伸缩(反射)变换,仅沿坐标轴方向伸缩(反射)变换。
2,对角矩阵可分解为多个F1矩阵,如下:

二,剪切矩阵
1,什么是剪切矩阵




2,剪切矩阵的几何意义


3,剪切矩阵的特点
变换前后面积不变
三,正交矩阵
1,什么是正交矩阵?


2,正交矩阵的特点
(1)是方阵
(2)每个列向量都是单位矩阵
(3)每对列向量都正交
(4)正交矩阵的转置等于它的逆
3,正交矩阵的几何意义
只有旋转,无剪切,无伸缩,无反射

如下图所示,矩阵A表示绕X轴旋转60°,矩阵B表示绕Z轴旋转45°,C表示先按X轴旋转60°再按Z轴旋转45°,顺序不能颠倒。


若颠倒顺序,先绕Z轴旋转,再按X轴旋转,则:

四,投影矩阵
1,什么是投影矩阵?
将高维的变换到低维


谱分解
作用对象是对称矩阵,对称矩阵的特征向量正交。
本质:将一个复杂的变换分解为:旋转-伸缩-逆旋转


Q为单位特征向量组成的矩阵,即e1,e2,e3都是单位特征向量,为特征值组成的对角矩阵。
过程解释(以2维为例):原对称矩阵S具有2个特征向量,且特征向量都正交,矩阵实现了将特征基 e1,e2旋转到原来的基 (1,0)(0,1)的过程,然后进行
伸缩变换,即沿特征基的方向进行伸缩变换,最后再乘Q将特征基旋转回原来的位置。
谱分解的特殊点:
(1)对称矩阵的特征向量都正交,原来的基也是正交的,则仅进行正交变换(旋转)即可实现将特征基旋转为原来的基。
奇异值分解
奇异值分解与谱分解的区别只有,谱分解是旋转---伸缩---逆旋转,而奇异值分解是旋转---伸缩(可能有维度消除或维度扩充)---再旋转。奇异值分解的第二次旋转不是第一次旋转的逆旋转。
1,图+公式推导

待分解矩阵的变换如图,改变换将相互正交的向量,
变换到仍然相互正交的向量
,
,伸缩量为
,
。设
,
,
则,即
即
即
所以的特征向量为
,特征值为
同理的特征向量为
,特征值为
综上,奇异值分解中,
为
的特征向量,
为
的特征向量。
为
或
特征值的平方根。
为右奇异向量,
为左奇异向量。
2,几何解释
相关文章:
【线性代数】矩阵变换
一些特殊的矩阵 一,对角矩阵 1,什么是对角矩阵 表示将矩阵进行伸缩(反射)变换,仅沿坐标轴方向伸缩(反射)变换。 2,对角矩阵可分解为多个F1矩阵,如下: 二&a…...

聚焦智慧出行,TDengine 与路特斯科技再度携手
在全球汽车行业向电动化和智能化转型的过程中,智能驾驶技术正迅速成为行业的焦点。随着消费者对出行效率、安全性和便利性的需求不断提升,汽车制造商们需要在全球范围内实现低延迟、高质量的数据传输和处理,以提升用户体验。在此背景下&#…...

虚拟机迁移报错:虚拟机版本与主机“x.x.x.x”的版本不兼容
1.虚拟机在VCenter上从一个ESXi迁移到另一个ESXi上时报错:虚拟机版本与主机“x.x.x.x”的版本不兼容。 2.例如从10.0.128.13的ESXi上迁移到10.0.128.11的ESXi上。点击10.0.128.10上的任意一台虚拟机,查看虚拟机版本。 3.确认要迁移的虚拟机磁盘所在位…...

【教程】vscode添加powershell7终端
win10自带的 powershell 是1.0版本的,太老了,更换为powershell7后,在 vscode 的集成终端中没有显示本篇教程记录在vscode添加powershell7终端的过程 打开vscode终端配置 然后来到这个页面进行设置 查看 powershell7 的安装位置ÿ…...

如何乘上第四次工业革命的大船
如何乘上第四次工业革命的大船 第四次工业革命通常被认为是信息技术和数字化时代的到来,但具体影响哪些产业,以及它将如何演变和展开,仍然是一个广泛讨论的话题。 然而,已经可以看到一些领域可能受到第四次工业革命的深远影响,例如人工智能、物联网、大数据、生物技术、可…...

RKNN执行bash ./build-linux_RK3566_RK3568.sh 报错
目录 报错信息: 原因分析: 解决办法: 报错信息: CMake Error at /usr/share/cmake-3.22/Modules/CMakeDetermineCCompiler.cmake:49 (message): Could not find compiler set in environment variable CC: aarch64-linux-gnu-gcc. Call Stack (most recent call fir…...

Linux常用命令整理
本文将分享一些常用的Linux命令。根据功能的不同,大概分为以下几个方面,一是文件相关命令,二是进程相关命令,三是网络相关命令,四是磁盘相关命令,五是用户管理相关命令,六是系统命令。 1. 文件…...
python 闭包、装饰器
一、闭包: 1. 外部函数嵌套内部函数 2. 外部函数返回内部函数 3.内部函数可以访问外部函数局部变量 闭包(Closure)是指在一个函数内部定义的函数,并且内部函数可以访问外部函数的局部变量,即使外部函数已经执行…...

[pycharm]解决pycharm运行程序出现卡住scanning files to index索引的问题
有时候会出现索引问题,显示scanning files to index 解决方法: in pycharm, go to the "File" on the left top, then select "invalidate caches/restart...", and press "invalidate and restart". 然后等它自己重启…...
)
python每日学习11:numpy库的用法(下)
python每日学习11:numpy库的用法(下) 数组的拼接 名方法称说明concatenate连接沿现有轴的数组序列hstack水平堆叠序列中的数组(列方向)vstack竖直堆叠序列中的数组(行方向)concatenate函数用于沿指定轴连接相同形状的两…...

【Emacs有什么优点,用Emacs写程序真的比IDE更方便吗?】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

6、基于Fabirc 2.X 通用电子存证系统部署
evidence 将GOPATH设置为/root/go,拉取项目: cd $GOPATH/src && git clone https://gitee.com/henan-minghua_0/evidence.git 在/etc/hosts中添加: 127.0.0.1 orderer.example.com 127.0.0.1 peer0.org1.example.com 127.0.0.1 peer1.org…...

Linux Vim 由浅入深的教程
引言 原文链接 Vim是Linux系统中非常强大的文本编辑器,因其强大的功能和灵活的操作而受到广泛使用。尤其是在服务器管理和开发环境中,Vim几乎是必备工具。本教程将以CentOS 7为例,详细讲解Vim的安装、基本操作以及一些高级技巧,…...

MIT6.824(6.5840) Lab1笔记+源码
文章目录 其他人的内容,笔记写的更好,思路可以去看他们的MapReduceworkermapreduce coordinatorrpc纠错 源码worker.gocoordinator.gorpc.go 原本有可借鉴的部分 mrsequential.go,多看几遍源码 其他人的内容,笔记写的更好…...
【目录】8051汇编与C语言系列教程
8051汇编与C语言系列教程 作者将狼才鲸创建日期2024-07-23 CSDN文章地址:【目录】8051汇编与C语言系列教程本Gitee仓库原始地址:才鲸嵌入式/8051_c51_单片机从汇编到C_从Boot到应用实践教程 一、本教程目录 序号教程名称简述教程链接1点亮LCD灯通过IO…...
群管机器人官网源码
一款非常好看的群管机器人html官网源码 搭建教程: 域名解析绑定 源码文件上传解压 访问域名即可 演示图片: 群管机器人官网源码下载:客户端下载 - 红客网络编程与渗透技术 原文链接: 群管机器人官网源码...

整合EasyExcel实现灵活的导入导出java
引入pom依赖 <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId></dependency>实现功能 结合Vue前端,实现浏览器页面直接导出日志文件实现文件的灵活导入文件导出 3. 实体类 实体类里有自定义转…...

springSecurity学习之springSecurity web如何取得用户信息
web如何取得用户信息 之前说过SecurityContextHolder默认使用的是ThreadLocal来进行存储的,而且每次都会清除,但是web每次请求都会验证用户权限,这是如何做到的呢? 这是通过SecurityContextPersistenceFilter来实现的࿰…...
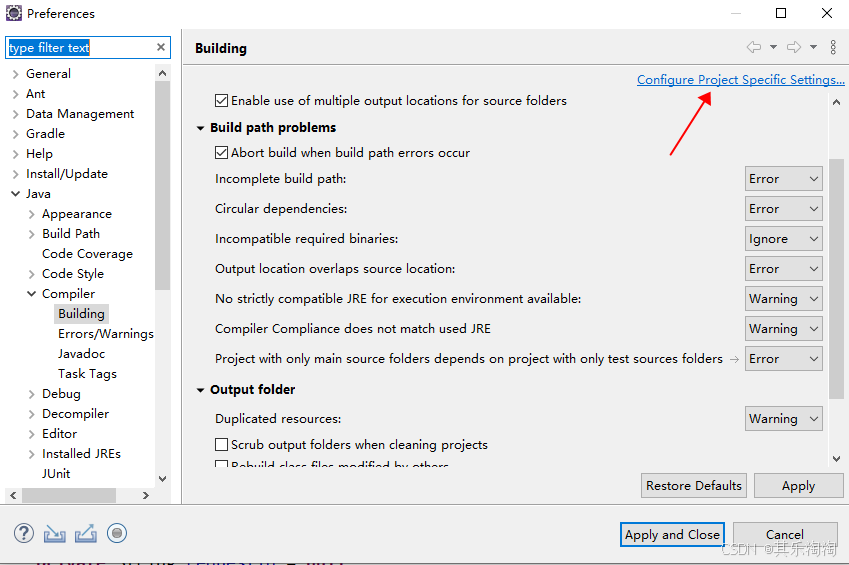
eclipse中的classbean导入外部class文件,clean项目后删除问题
最近被eclipse搞得头疼,下午终于解决 eclipse创建的java项目中,类的输出目录是classbean。由于项目需要,classbean目录下已经导入了外部的类,但每次clean项目时,会把class删掉。 广泛查询,eclipse不清空c…...
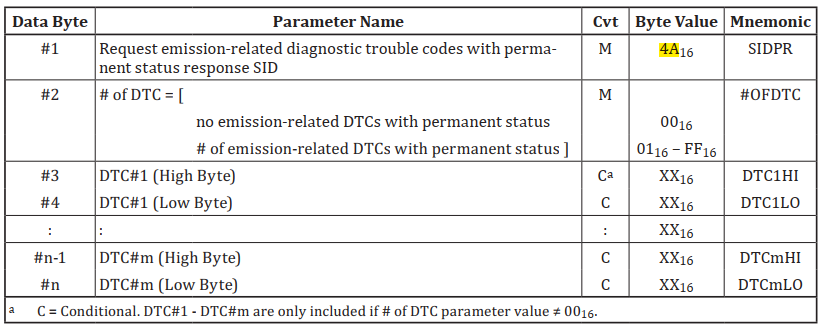
OBD诊断(ISO15031) 0A服务
文章目录 功能简介ISO 15765-4的诊断服务定义1、请求具有永久状态的排放相关故障诊断码2、请求具有永久状态的排放相关故障诊断码3、示例报文 功能简介 0A服务,即 Request emission-related diagnostic trouble code with permanent status(请求排放相关…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
