【算法/学习】前缀和差分
前缀和&&差分目录
1. 前缀和的概念及作用
🌈概念
🌈用途
🌙一维前缀和
🌙二维前缀和
2. 差分的概念及用途
🌈概念:
🌈用途
🌙一维差分
🌙二维差分
1. 前缀和的概念及作用
🌈概念
前缀和:
🎈对于一个给定的数列a,他的前缀和数中 s 中 s[ i ] 表示从第一个元素到第 i 个元素的总和。即s[ i ] = s[ i - 1 ] + a[ i ];
比如: s[ 1 ] = s[ 0 ] + a[ 1 ]。
注意:在使用前缀和和差分的时候,一般下标 0 不参与的运算,统一的将下表设置为从1开始,具体是要考虑到我们的边界问题,也就是S[1]的求法问题,为了保证我们循环的统一性,我们要将S[0]设置为0,所以我们索性就将下标从1开始设置起,这样也有利于我们后面的初始化。
🌈用途
可以用于一维前缀和和二维前缀和。
模板如下:
🌙一维前缀和
核心代码如下:
s[i] = s[i-1] + a[i]
s[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = s[r] - s[l - 1]🧩例题如下:
题目练习: AcWing 795. 前缀和

思路:
首先做一个预处理,定义一个s数组,让s[ i ]代表 a 数组前 i 个数的和。
然后运用求一维前缀和运算的公式 s[i] = s[i-1] + a[i] 。
再进行查询操作:即s[ r ] - s[ l - 1] ,这样使得求 [ l, r ]的和的时间复杂度变为 O (1).
注意:求 [ l, r ]的和是s[ r ] - s[ l - 1],之所以要 l - 1是因为,a[ l ] 也包括在内
因为a[l] + ... + a[r] = s[r] - s[l - 1]
AC代码如下:
#include <iostream>
using namespace std;const int N = 1e5+10;
int a[N], s[N];int main(){int n, m, x;cin>>n>>m;for(int i = 1; i <= n; i++) cin>>a[i];for(int i = 1; i <= n; i++) s[i] = a[i] + s[i - 1];int l, r;while(m--){cin>>l>>r;cout<<s[r] - s[l - 1]<<endl;}return 0;
}🌙二维前缀和
和一维前缀和的原理类似,只不过二维前缀和求的是一个矩阵中所有元素的和。
如下图:

因此通过上面的图我们就可以更好理解下图来推导公式了:


s[ i ][ j ] 即为框内所有数的和:s[ i ][ j ]=s[ i ][ j - 1 ]+s[ i - 1 ][ j ] - s[ i - 1 ][ j - 1 ]+a[ i ][ j ];
而(x1, y1) 到 (x2, y2)的矩阵大小为s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]
核心代码:
s[x][y]=s[x][y-1]+s[x-1][y]-s[x-1][y-1]+a[x][y];
s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]🧩例题如下:
题目练习: AcWing 796. 子矩阵的和

思路:
先做一个预处理,定义一个s矩阵,s[ i ][ j ]代表 a 矩阵前 从(0,0)到(i,j)的矩阵和。
然后运用求一维前缀和运算的公式 s[i] = s[i-1] + a[i] 。
再进行查询操作:即s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]。
这样使得求 (x1, y1) 到 (x2, y2)的矩阵大小的和的时间复杂度变为 O (1).
AC代码如下:
#include <iostream>
using namespace std;const int N = 1005;
int a[N][N], s[N][N];int main(){int n, m, q;cin >> n >> m >> q;//第一步:输入矩阵的值for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cin >> a[i][j];}}//第二步:求矩阵前缀和for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++) {s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];}}//第三步:查找(x1,y1)到(x2,y2)的矩阵大小while (q--){int x1, x2, y1, y2;cin >> x1 >> y1 >> x2 >> y2;printf("%d\n", s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]);}return 0;
}
2. 差分的概念及用途
🌈概念:
差分:
🎈 类似于数学中的求导和积分,差分可以看成前缀和的逆运算
对于一个给定的数列a,其中a[1],a[2]…a[n]作为前缀和。它的差分数组中 b 中 b[ i ] 表示从第 i - 1个元素到第 i 个元素的差值。即b[ i ] = a[ i ] - s[ i - 1 ];
一维差分数组的构造也很简单,即a[1] = b[1], b[2] = a[2] - a[1], b[n] = a[n] - a[n-1];
注意:刚开始时可以初始化数组a,b全部为0,输入a数组后;在构造时,只需要将b[1]看做在[1, 1]区间上加上a[1]; b[2] 看作在[2, 2]区间上加上a[2];
🌈用途
🌙一维差分
差分数组的好处是可以简化运算,例如想要给一个区间 [l,r] 上的数组加一个常数c,原始的方法是依次加上c,这样的时间复杂度是O(n)的。但是如果采用差分数组的话,可以大大降低时间复杂度到O(1)。
因此只需要将b[l] = b[l] + c 即可,这样l之后的数字会依次加上常数c,而在 b[r]处,将b[r+1] = b[r+1] - c ,这样r之后的数组又会恢复原值,仅需要处理这两个边界的差分数组即可。时间复杂度大大降低。
核心代码如下:
b[i]=a[i]-a[i-1];
a[i] = b[i] + a[i - 1];🧩例题如下:
题目练习: AcWing 797. 差分

思路:
首先做一个预处理,定义一个b数组,让b[ i ]代表a[ i ] - a[ i -1 ].
因此只需要将b[l] = b[l] + c 即可,这样l之后的数字会依次加上常数c,而在 b[r]处,将b[r+1] = b[r+1] - c ,这样r之后的数组又会恢复原值,仅需要处理这两个边界的差分数组即可。
AC代码如下:
#include <iostream>
using namespace std;const int N = 1e5 + 5;
int b[N], a[N];int main()
{int n, m;cin>>n>>m;for (int i = 1; i <= n; i++){scanf("%d", &a[i]);b[i]=a[i]-a[i-1];}while(m--){int l,r,c;cin>>l>>r>>c;b[l]+=c;b[r+1]-=c;}for (int i = 1; i <= n; i++){a[i] = b[i] + a[i - 1];printf("%d ", a[i]);}return 0;
}🌙二维差分
如果扩展到二维,我们需要让二维数组被选中的子矩阵中的每个元素的值加上c,是否也可以达到O(1)的时间复杂度。答案是可以的,考虑二维差分。
a[][]数组是b[][]数组的前缀和数组,那么b[][]是a[][]的差分数组原数组:
a[i][j]我们去构造差分数组:
b[i][j]使得
a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。
如何构造b数组呢?
其实关于差分数组,我们并不用考虑其构造方法,因为我们使用差分操作在对原数组进行修改的过程中,实际上就可以构造出差分数组。
同一维差分,我们构造二维差分数组目的是为了 让原二维数组a中所选中子矩阵中的每一个元素加上c的操作,可以由O(n*n)的时间复杂度优化成O(1)
已知原数组a中被选中的子矩阵为 以(x1,y1)为左上角,以(x2,y2)为右下角所围成的矩形区域;
始终要记得,a数组是b数组的前缀和数组,比如对b数组的b[i][j]的修改,会影响到a数组中从a[i][j]及往后的每一个数。
假定我们已经构造好了b数组,类比一维差分,我们执行以下操作
来使被选中的子矩阵中的每个元素的值加上c
b[x1][y1] + = c ;
b[x1,][y2+1] - = c;
b[x2+1][y1] - = c;
b[x2+1][y2+1] + = c;
每次对b数组执行以上操作,等价于:

b[x1][y1] += c ; 对应图1 ,让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1,][y2 + 1] -= c ; 对应图2 ,让整个a数组中绿色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2 + 1][y1] -= c ; 对应图3 ,让整个a数组中紫色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2 + 1][y2 + 1] += c; 对应图4,让整个a数组中红色矩形面积的元素再加上c,红色内的相当于被减了两次,再加上一次c,才能使其恢复。
核心代码如下:
b[i][j] = a[i][j] − a[i − 1][j] − a[i][j − 1] + a[i −1 ][j − 1]
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
题目练习: AcWing 798. 差分矩阵


AC代码如下:
#include <iostream>
using namespace std;const int N = 1005;
int a[N][N], b[N][N];int main(){int n, m, q;cin >> n >> m >> q;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++) {cin >> a[i][j];b[i][j] = a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];}}while (q--){int x1, x2, y1, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;b[x1][y1] += c, b[x2 + 1][y2 + 1] += c;b[x1][y2 + 1] -= c, b[x2 + 1][y1] -= c;}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];cout << a[i][j] << " ";}cout << endl;}return 0;
}
相关文章:

【算法/学习】前缀和差分
前缀和&&差分目录 1. 前缀和的概念及作用 🌈概念 🌈用途 🌙一维前缀和 🌙二维前缀和 2. 差分的概念及用途 🌈概念: 🌈用途 🌙一维差分 🌙二维差分 1. …...

idea Project 不显示文件和目录
idea Project 不显示文件和目录 File - Close Project - 重新打开项目即可删除.idea文件夹,重新打开项目即可。 原因分析: 可能与使用不同ide例如java、python打开同一项目有关 参考: https://blog.csdn.net/hgnuxc_1993/article/details/132595900 解决打开IDE…...

Linux--Socket编程预备
目录 1. 理解源 IP 地址和目的 IP 地址 2.端口号 2.1端口号(port)是传输层协议的内容 2.2端口号范围划分 2.3理解 "端口号" 和 "进程 ID" 2.4理解 socket 3.传输层的典型代表 3.1认识 TCP 协议 3.2认识 UDP 协议 4. 网络字节序 5. socket 编程接…...

100个python的基本语法知识【下】
50. 压缩文件: import zipfilewith zipfile.ZipFile("file.zip", "r") as zip_ref:zip_ref.extractall("extracted")51. 数据库操作: import sqlite3conn sqlite3.connect("my_database.db") cursor conn.c…...

Git如何将一个分支上的修改转移到另一个分支
在我们使用git进行版本控制时,当代码写错分支,怎么将这些修改转移到正确的分支上去呢?这时,我们可以使用git stath命令来暂存我们的修改,然后再切换到其他分支 未commit(提交)操作时 1. 先将修…...

jvm-证明cpu指令是乱序执行的案例
package jvm;/*** 证明cpu指令是乱序执行的** author 1* version 1.0* description: TODO* date 2024-07-19 9:31*/ public class T04_Disorder {private static int x 0, y 0;private static int a 0, b 0;public static void main(String[] args) throws InterruptedExcep…...

《流程引擎原理与实践》开源电子书
流程引擎原理与实践 电子书地址:https://workflow-engine-book.shuwoom.com 第一部分:流程引擎基础 1 引言 1.1 流程引擎介绍 1.2 流程引擎技术的发展历程 1.3 相关产品国内外发展现状 1.4 本书的内容和结构安排 2 概念 2.1 基础概念 2.2 进阶…...

谷粒商城实战笔记-52~53-商品服务-API-三级分类-新增-修改
文章目录 一,52-商品服务-API-三级分类-新增-新增效果完成1,点击Append按钮,显示弹窗2,测试完整代码 二,53-商品服务-API-三级分类-修改-修改效果完成1,添加Edit按钮并绑定事件2,修改弹窗确定按…...

uni-app 影视类小程序开发从零到一 | 开源项目分享
引言 在数字娱乐时代,对于电影爱好者而言,随时随地享受精彩影片成为一种日常需求。分享一款基于 uni-app 开发的影视类小程序。它不仅提供了丰富的影视资源推荐,还融入了个性化知乎日报等内容,是不错的素材,同时对电影…...

Python使用正则替换字符串
Python小技:使用正则替换字符串 java中有String.replaceAll()方法使用正则替换字符串, 在Python中,字符串也有一个replace方法,但是这个方法只能精准替换, 如果想正则替换,就要改成re.sub方法,而…...

每日一练,java03
目录 题目wait()、notify()和notifyAll()方法的特性和使用场景wait() 方法notify() 方法notifyAll() 方法使用场景 注意事项 题目 选自牛客网 1.下面关于JAVA的垃圾回收机制,正确的是( ) A.当调用“System.gc()”来强制回收时,系…...

【机器学习】深入理解损失函数(Loss Functions)
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 深入理解损失函数(Loss Functions)什么是损失函数?常见损失函数类型1. 均方误差…...

python实现特征检测算法3
python实现SIFT(尺度不变特征变换)算法、SURF(Speeded Up Robust Features)算法 1.SIFT算法详解算法步骤Python实现详细解释优缺点应用领域2.SURF算法详解算法步骤Python实现详细解释SURF算法原理优缺点应用领域尺度不变特征变换(SIFT,Scale-Invariant Feature Transform…...

软件更新的双刃剑:从”微软蓝屏”事件看网络安全的挑战与对策
引言 原文链接 近日,一场由微软视窗系统软件更新引发的全球性"微软蓝屏"事件震惊了整个科技界。这次事件源于美国电脑安全技术公司"众击"提供的一个带有"缺陷"的软件更新,如同一颗隐形炸弹在全球范围内引爆,…...

Redis 主从搭建
Redis主从搭建 7.2.5 文章目录 一. 同主机搭建Redis主从1. 环境介绍2. 环境前准备工作3. 安装 Redis 7.2.54. redis 配置修改并且启动4.1 修改配置文件4.2 编写启动脚本 5. 开启主从5.1 开启5.2 主库实例查看主从信息5.3 从库实例查看主从信息5.4 验证主从配置是否生效 6. 解除…...

LeetCode 129, 133, 136
文章目录 129. 求根节点到叶节点数字之和题目链接标签思路代码 133. 克隆图题目链接标签思路代码 136. 只出现一次的数字题目链接标签思路代码 129. 求根节点到叶节点数字之和 题目链接 129. 求根节点到叶节点数字之和 标签 树 深度优先搜索 二叉树 思路 由于本题需要 从…...

macOS 环境Qt Creator 快捷键
在 macOS 环境下,Qt Creator 是一个流行的集成开发环境(IDE),用于开发 Qt 项目。下面是一些常用的快捷键和操作技巧,帮助你更高效地使用 Qt Creator 进行项目开发和管理: 在 macOS 中,Cmd 键 四…...

【C# WInForm】将TextBox从输入框设置为文本框
1.需求情形: textbox作为最常用的控件之一,通常是用来输入文本信息或者显示文字,但是如果要在界面中显示大段文本,一个带有边框、可选中的文本样式似乎不合适。像这样: 我需要的是这段文字不仅能跨行,而且…...

minio 服务docker配置
用minio docker配置了一个服务,分享链接始终是127.0.01开始的, 改成docker的host的ip则提示签名不匹配, 好在这个文件主要是用来下载的,所以可以通过设置bucket的匿名访问权限来实现下载; 这样不需要后面的地址参数就…...
)
开源模型应用落地-LangChain高阶-智能体探究-自定义agent(五)
一、前言 大模型具有非常强大的功能,可以解答疑问、撰写报告和文档、总结内容、进行翻译等各种日常工作任务。然而,大模型还可以应用于更多的场景,发挥出更强大的作用。 通过智能体,我们可以实现许多有价值的事情,比如:在日常生活中,我们能借助智能体实现智能家居的自动化…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

python读取SQLite表个并生成pdf文件
代码用于创建含50列的SQLite数据库并插入500行随机浮点数据,随后读取数据,通过ReportLab生成横向PDF表格,包含格式化(两位小数)及表头、网格线等美观样式。 # 导入所需库 import sqlite3 # 用于操作…...
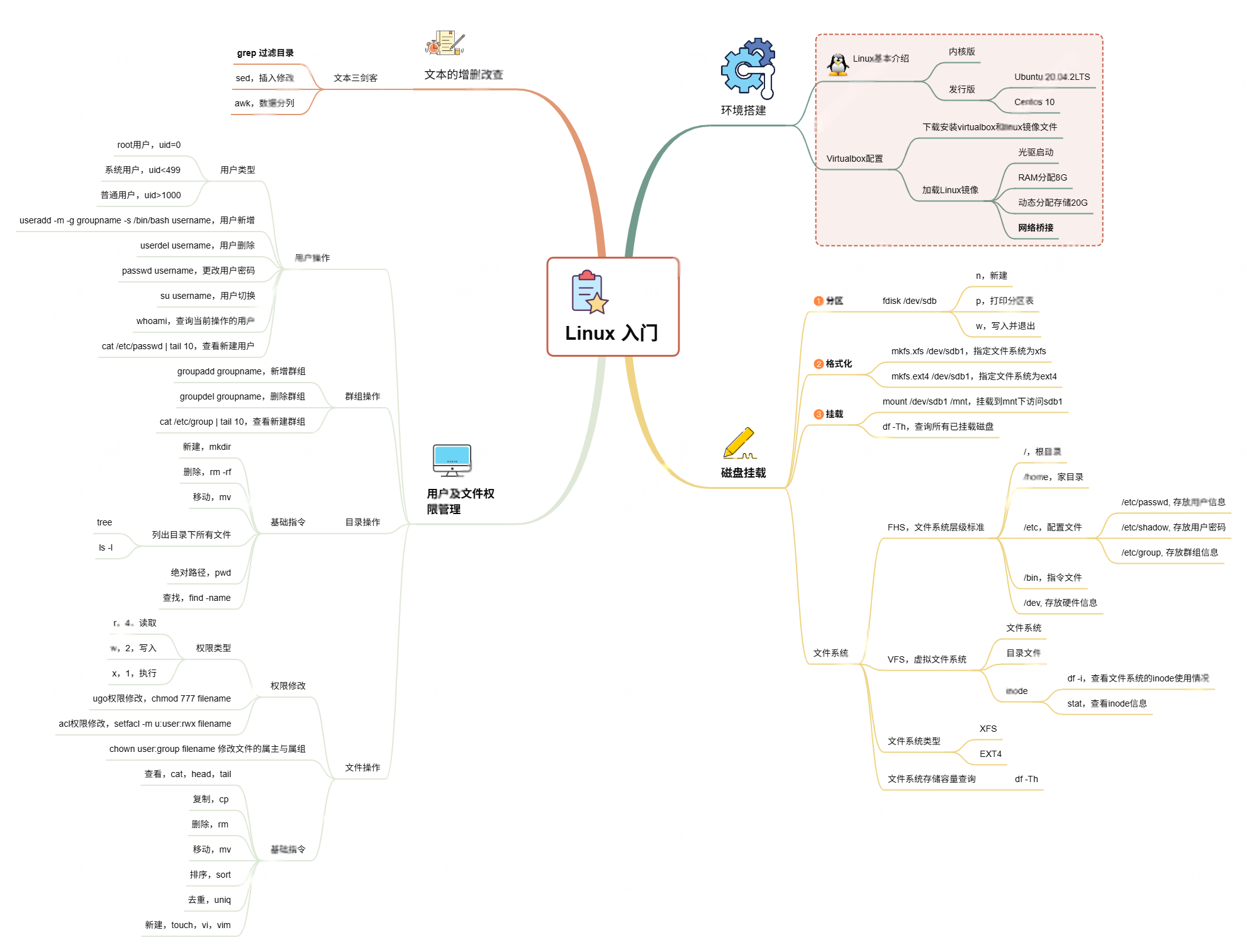
Linux入门课的思维导图
耗时两周,终于把慕课网上的Linux的基础入门课实操、总结完了! 第一次以Blog的形式做学习记录,过程很有意思,但也很耗时。 课程时长5h,涉及到很多专有名词,要去逐个查找,以前接触过的概念因为时…...

Linux系统:进程间通信-匿名与命名管道
本节重点 匿名管道的概念与原理匿名管道的创建命名管道的概念与原理命名管道的创建两者的差异与联系命名管道实现EchoServer 一、管道 管道(Pipe)是一种进程间通信(IPC, Inter-Process Communication)机制,用于在不…...

统计按位或能得到最大值的子集数目
我们先来看题目描述: 给你一个整数数组 nums ,请你找出 nums 子集 按位或 可能得到的 最大值 ,并返回按位或能得到最大值的 不同非空子集的数目 。 如果数组 a 可以由数组 b 删除一些元素(或不删除)得到,…...
