1858. 数组查找及替换
问题描述
给定某整数数组和某一整数 b 。
要求删除数组中可以被 b 整除的所有元素,同时将该数组各元素按从小到大排序。如果数组元素数值在 '𝐴‘ 到 'Z' 的 ASCII 之间,替换为对应字母。
元素个数不超过 100,𝑏 在 1 至 100 之间。
输入
第一行为表示数组元素个数 N 和整数 b。(1≤𝑁≤100)
第二行为数组各个元素。
输出
按照要求输出。

附代码:
#include<iostream>
using namespace std;
int main()
{
int N,b,x=0,temp;
cin>>N>>b;
if(N>=1&&N<=100)
{
int a[N];
for(int i=0;i<N;i++)
{
cin>>a[i];
}
for(int i=0;i<N;i++)
{
if(a[i]%b!=0)
{
a[x]=a[i];
x++;
}
}
for(int y=0;y<x-1;y++)
{
if(a[y]>a[y+1])
{
temp=a[y];
a[y]=a[y+1];
a[y+1]=temp;
}
}
for(int y=0;y<x;y++)
{
if(a[y]>64&&a[y]<91)
cout<<char(a[y])<<" ";
else
cout<<a[y]<<" ";
}
}
return 0;
}
相关文章:

1858. 数组查找及替换
问题描述 给定某整数数组和某一整数 b 。 要求删除数组中可以被 b 整除的所有元素,同时将该数组各元素按从小到大排序。如果数组元素数值在 𝐴‘ 到 Z 的 ASCII 之间,替换为对应字母。 元素个数不超过 100,𝑏 在 1 …...
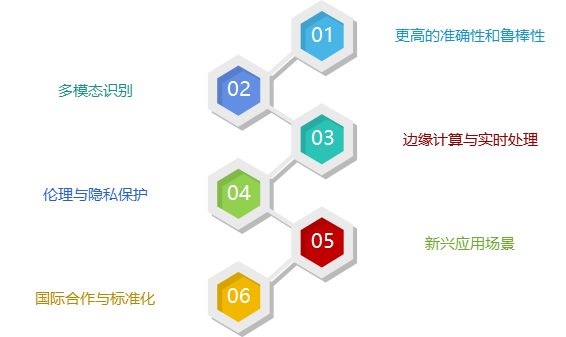
计算机视觉与面部识别:技术、应用与未来发展
引言 在当今数字化时代,计算机视觉技术迅速发展,成为人工智能领域的一个重要分支。计算机视觉旨在让机器理解和解释视觉信息,模拟人类的视觉系统。它在各行各业中发挥着重要作用,从自动驾驶汽车到智能监控系统,再到医疗…...

懒人精灵安卓版纯本地离线文字识别插件
目的 懒人精灵是一款可以模拟鼠标和键盘操作的自动化工具。它可以帮助用户自动完成一些重复的、繁琐的任务,节省大量人工操作的时间。懒人精灵也包含图色功能,识别屏幕上的图像,根据图像的变化自动执行相应的操作。本篇文章主要讲解下更优秀的…...

在线教育数仓项目(数据采集部分1)
文章目录 数据仓库概念项目需求及架构设计项目需求分析系统数据流程设计框架版本选型集群规模估算集群资源规划设计 数据生成模块目标数据页面事件曝光启动播放错误 数据埋点主流埋点方式(了解)埋点数据上报时机埋点数据日志结构 服务器和JDK准备服务器准…...

帕金森病(PD)诊断:三种基于语音的深度学习方法
帕金森病(Parkinson’s disease, PD)是世界上第二大流行的神经退行性疾病,全球影响着超过1000万人,仅次于阿尔茨海默症。人们通常在65岁左右被诊断出患有此病。PD的一些症状包括震颤、肌肉僵硬和运动迟缓。这些症状往往出现在较晚…...

【资料分享】2024钉钉杯大数据挑战赛A题思路解析+代码演示
2024第三届钉钉杯大学生大数据挑战赛今天已经开赛,【A题】思路解析代码,资料预览:...

【优质精选】12节大模型系列教学课程之二:RAG 原理与应用
课程二:RAG 原理与应用 12节大模型系列教学课程之二:RAG 原理与应用 课程详细内容RAG 技术的基础知识RAG 的工作原理RAG 提高生成质量和准确性的原理RAG 在问答系统中的应用RAG 在文本创作中的应用RAG 在其他领域的应用探索RAG 技术的挑战与应对策略RAG …...

vue3前端开发-小兔鲜项目-产品详情基础数据渲染
vue3前端开发-小兔鲜项目-产品详情基础数据渲染!这一次内容比较多,我们分开写。第一步先完成详情页面的基础数据的渲染。然后再去做一下右侧的热门产品的列表内容。 第一步,还是老规矩,先准备好接口函数。方便我们的页面组件拿到对…...

Docker入门指南:Linux系统下的完整安装步骤与常见问题解答
本文以centos7演示。 Docker安装 可参考官方安装文档:Install Docker Engine on CentOS | Docker Docs 一图流: # 移除旧版本docker sudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logro…...

Netty实现数据上下行
Netty实现数据上下行 使用LVSNGinxNetty实现数据接入 在数据上行的时候,通过使用车辆唯一标识码(vin)和连接通道绑定 Netty一些配置参数如下: #netty项目使用的端口 server.port8017 #使用启用epoll(在Linux上拥有更好的传输性…...

【React】事件绑定:深入解析高效处理用户交互的最佳实践
文章目录 一、什么是事件绑定?二、基本事件绑定三、绑定 this 上下文四、传递参数五、事件对象六、事件委托七、常见事件处理八、优化事件处理 React 是现代前端开发中最受欢迎的框架之一,其组件化和高效的状态管理能力使得构建复杂的用户界面变得更加容…...

SpringCloud:使用OpenFeign优化前面的Nacos实现高效购物车商品信息处理
在现代电商系统中,购物车的性能直接影响用户的购物体验。为了提升系统性能和用户满意度,我们可以使用Spring Cloud的OpenFeign和负载均衡器来高效地处理购物车中的商品信息。本文将详细介绍如何在Spring Cloud中集成这些组件,并实现一个高效的…...

计算机三级嵌入式笔记(二)——嵌入式处理器
目录 考点1 嵌入式处理器的结构类型 考点2 嵌入式处理器简介 考点3 ARM处理器概述 考点4 处理器和处理器核 考点5 ARM 处理器的分类 考点6 经典 ARM 处理器 考点7 ARM Cortex 嵌入式处理器 考点8 ARM Cortex实时嵌入式处理器 考点9 ARM Cortex 应用处理器 考点10 AR…...

【GoLang】Golang 快速入门(第一篇)
目录 1.简介: 2.设计初衷: 3.Go语言的 特点 4.应用领域: 5.用go语言的公司: 6. 开发工具介绍以及环境搭建 1.工具介绍: 2.VSCode的安装: 3.安装过程: 4.Windows下搭建Go开发环境--安装和配置SDK 1.搭建Go开发环境 - 安装…...

Linux中的三类读写函数
文件IO和标准IO的区别 遵循标准: 文件IO遵循POSIX标准,主要在类UNIX环境下使用。标准IO遵循ANSI标准,具有更好的可移植性,可以在不同的操作系统上重新编译后运行。可移植性: 文件IO的可移植性相对较差,因为…...

MATLAB基础应用精讲-【数模应用】二元Probit回归分析
目录 前言 知识储备 二元Logistic模型和Probit模型 Logistic模型的形式 Probit模型 优势比(OR) 准二项分布族 算法原理 数学模型 二元因变量和线性概率模型 probit和logit回归 logit和probit模型的估计和推断 稳健性检验 二元logit回归分析全流程 一、案例数…...

找工作准备刷题Day10 回溯算法 (卡尔41期训练营 7.24)
回溯算法今天这几个题目做过,晚上有面试,今天水一水。 第一题:Leetcode77. 组合 题目描述 解题思路 从题目示例来看,k个数是不能重合的,但是题目没有明确说明这一点。 使用回溯算法解决此问题,利用树形…...

如何有效的进行小程序的优化
如今小程序已经成为了许多开发者开展业务,提供服务的重要平台 。所以如何有效的优化小程序成为了开发者关注的首要问题,以下是一份详细的小程序优化方案: 一、目标设定 明确小程序优化的主要目标,例如提高用户留存率、增加用户活…...

FPGA-ROM IP核的使用(2)
前言 接着昨天的进行一个小的实验验证ROM IP核。 实验效果 读取上一期生成的IP核中的数据,并将其显示在数码管上。 具体流程 ROM IP核存放数据0~255,之后每隔0.2s,从0的地址开始读数据,并显示在数码管上;接着先后…...

Manticore Search(es轻量级替代)
概念: Manticore Search 是一个使用 C 开发的高性能搜索引擎,创建于 2017 年,其前身是 Sphinx Search 。Manticore Search 充分利用了 Sphinx,显着改进了它的功能,修复了数百个错误,几乎完全重写了代码并保…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
