《算法笔记》总结No.11——数字处理(上)欧拉筛选
机试中存在部分涉及到较复杂数字的问题,这是编码的基本功,各位一定要得心应手。

目录
一.最大公约数和最小公倍数
1.最大公约数
2.最小公倍数
二.素数
1.判断指定数
2.输出所有素数
3.精进不休——埃拉托斯特尼筛法
4.达到更优!——欧拉筛法
一.最大公约数和最小公倍数
初学就开始的老生常谈,比较基础,大一期末考试和普通学校考研的难度,一定不要掉以轻心。
1.最大公约数
这里我们用欧几里得算法来实现——其实也就是初中学过的辗转相除法,没什么难度~
int gcb(int x,int y)
{if(x<y) //保证前者更大一些 {int temp=x;x=y;y=temp;}while(y!=0){int temp=y;y=x%y;x=temp;} return x;
}2.最小公倍数
设最大公约数是z,则x和y的最小公倍数就是x*y/z,这个公式也是小学知识,不要忘了;要是考试的时候真不小心忘了,就用暴力枚举吧,从x和y大的一个开始直到第一个可以同时整除x和y的元素即为最小公倍数~
int main() {int x=0,y=0; cout<<"请输入两个数:";cin>>x>>y;cout<<"最大公约数是:"<<gcb(x,y)<<endl;cout<<"最小公倍数是:"<<(x*y)/gcb(x,y)<<endl;}没什么问题:

二.素数
1.判断指定数
常规的暴力枚举复杂度度为O(N),其实有更为简洁的办法——即对目标数开根号,比如对于16来说,2就是其的一个约数,但是16/2也是其一个约数,显然我们并不需要枚举到8——因为对于一个数来说,既然能整除,那么约数肯定是成对出现的,因此其中一个肯定比16开根号小,另一个则肯定大,所以我们只需要枚举到4(也就是开根号),就能判断目标数字是否为素数~
bool IsPrime(int x)
{int temp=sqrt(x);for(int i=2;i<=temp;i++)if(x%i==0)return false;return true;
}非常简单,不再赘述~
2.输出所有素数
上面函数已经有了,我们只需要枚举范围内的元素并调用函数,即可输出全部的素数:
int main() {int x=0;cout<<"请输入查询的最大值:"; cin>>x;int count=0;for(int i=1;i<=x;i++){if(IsPrime(i)){cout<<i<<" ";count++;}if(count==5){cout<<endl;count=0;}}
}没什么bug,count是为了输出更美观附加的:

3.精进不休——埃拉托斯特尼筛法
不妨这样思考一下:假设2是素数的话,那么他的倍数——4/6/8/10等等,一切可以整除2的数——是不是都不是素数!因此当我们找到一个素数时,如果将他的全部倍数都标记为合数,岂不是大大增加了效率。事实上,这就是埃拉托斯特尼筛法,其复杂度为LogN的平方,复杂度还要小于前面的N*根号N!代码如下:
#include <iostream>
#include <vector>
#include <cmath>using namespace std;void Eratos(int x)
{vector<int> Num,answer;Num.push_back(-1);//统一vector中的数字与下标 for(int i=1;i<=x;i++)Num.push_back(0); //初始化数组,如果下标i是0,则代表i是素数for(int i=2;i<x;i++){if(Num[i]==0){answer.push_back(i);for(int j=i+i;j<x;j+=i)//如果i是素数,则i所有的倍数都不是素数! Num[j]=1; } } for(int k=0;k<=answer.size()-1;k++)cout<<answer[k]<<" ";
}int main() {int x=0;cout<<"请输入查询的最大值:"; cin>>x;Eratos(x);
}没什么问题:

诸位不妨仔细品味一下这个筛选的方法及其实现——是不是又有散列,又有二分的思想?何其妙哉~
4.达到更优!——欧拉筛法
实际上,埃拉托斯特尼筛法还是有其优化的余地:比如6、10两个数字:按照其规则,这两个数在2的时候已经判断不是素数了,但是当枚举到3和5的时候,实际上还要再判断一次!
因此不妨保证——每个合数只是被自己最小的质因数找到,这样就避免了重复的筛选步骤。为了防止大家晕,这里修改一下埃式筛的代码:
#include <iostream>
#include <vector>
#include <cmath>using namespace std;void Eratos(int x)
{int times=0;int count=0;//记录当前素数的个数vector<int> answer;//存放所有的素数vector<int> Num;//标记Num.push_back(0);//统一下标和数字大小 for(int i=1;i<=x;i++)Num.push_back(0);for(int i=2;i<=x;++i){if(!Num[i]){answer.push_back(i);count++;}for(int j=0;j<count;++j){if(i*answer[j]>x)break;int temp=i*answer[j];Num[temp]=1;times++;
// if (i % answer[j] == 0)
// break;}} for(int k=0;k<=answer.size()-1;k++)cout<<answer[k]<<" ";cout<<endl;cout<<"共标记了:"<<times<<"次!";
} int main() {int x=0;cout<<"请输入查询的最大值:"; cin>>x;Eratos(x);
}我们来测试一下100,可以发现标记合数的步骤一共执行了104次:

我们仔细回溯一下如上代码的运行流程:
- 当i=2时,是素数,因此放到answer数组中;接下来遍历answer数组,2*2=4,因此4肯定不是素数,标记为合数
- 接下来i=3,是素数,因此放到answer数组中;接下来遍历answer,3*2=6,3*3=9,因此6和9均被标记为合数
- 接下来i=4,不是素数,直接遍历answer,2*4=8,3*4=12,8应该被标记为合数,但是对于12,其最小约数是2,因此应该由6*2来标记,所以此刻应该直接跳过
因此就有了有欧拉的写法:
void Eratos(int x)
{int times=0;int count=0;//记录当前素数的个数vector<int> answer;//存放所有的素数vector<int> Num;//标记Num.push_back(0);//统一下标和数字大小 for(int i=1;i<=x;i++)Num.push_back(0);for(int i=2;i<=x;++i){if(!Num[i]){answer.push_back(i);count++;}for(int j=0;j<count;++j){if(i*answer[j]>x)break;int temp=i*answer[j];Num[temp]=1;times++;if (i % answer[j] == 0)break;}} for(int k=0;k<=answer.size()-1;k++)cout<<answer[k]<<" ";cout<<endl;cout<<"共标记了:"<<times<<"次!";
}核心在于这个:大家自行品味妙处——对于上面来说,因为4已经遇到了最小质因数2,因此应该直接跳出循环!

运行100以内的素数,只执行了74次!

我们再来拿1000测试一下:

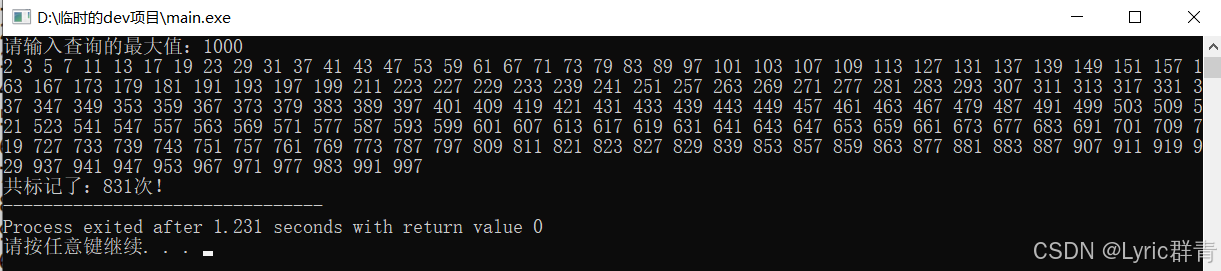
埃氏筛用了1400多次,而欧式筛只用了800多次,高低立判!
今天就先总结到这,希望如上的素数搜索,对各位思考算法的意义有所启发——当人力无法计算庞大的运算量时,计算机应运而生;而计算机由于计算方式的不同,效率也不尽相同。我们追求高效简洁的算法,因为越低的耗时标志着越高的生产力——而相信各位都学过马克思主义基本原理:社会变革的根本原因是生产力的发展~博主有幸拜读过《人月神话》,相信大家都清楚【银弹】对于软件工程的意义。或许对于银弹的不懈追求,正是人类能够进化的原因~
相关文章:

《算法笔记》总结No.11——数字处理(上)欧拉筛选
机试中存在部分涉及到较复杂数字的问题,这是编码的基本功,各位一定要得心应手。 目录 一.最大公约数和最小公倍数 1.最大公约数 2.最小公倍数 二.素数 1.判断指定数 2.输出所有素数 3.精进不休——埃拉托斯特尼筛法 4.达到更优!——…...

DP学习——享元模式
学而时习之,温故而知新。 享元模式 名词解析 有必要解释下“享元”两字,英文原文是flyweight pattern——轻量级模式,但是翻译过来的“享元”两字太牛逼了——褒贬不一,翻译的他妈都不认识。 享元的高雅在于: 享:共享/共用 元:…...

无人机10公里WiFi图传摄像模组,飞睿智能超清远距离无线监控,智能安防新潮流
在这个科技日新月异的时代,我们对影像的捕捉和传播有了更高的要求。从传统的有线传输到无线WiFi图传,每一次技术的飞跃都为我们带来了全新的视觉体验。今天,我们要探讨的,正是一款具有划时代意义的科技产品——飞睿智能10公里WiFi…...

SAP S/4HANA Cloud Public Edition
即装即用的云ERP软件。借助SaaS模式为企业提供完备、现代化的ERP 云套件,为企业带来新的技术突破,如自动化的业务流程与基于数据的商业分析。企业可选择这款智能云ERP软件,快速实现自身价值。 什么是 SAP S/4HANA Cloud Public Edition&#…...
LabVIEW汽车动态信号模拟系统
随着汽车工业的快速发展,对汽车电子控制单元(ECU)的测试与仿真需求日益增加。开发了一种基于LabVIEW软件开发的汽车动态信号模拟系统,该系统能有效模拟ECU在实车环境下的工作状态,为ECU的开发和测试提供了一个高效、经…...

chrome 插件:content-script 部分逻辑在页面无法生效,可考虑插入 script 到页面上
背景: 某页面有个输入框, 用的应该是什么库里的组件, 直接修改内容不生效/机制不明确, 于是使用 paste event 粘贴到输入框, 结果发现也不行 定位: 使用 mutationObserver , 发现事件确实触发了, 输入框内容变了, 但马上又变回来了, 于是怀疑是输入框组件有做 mutationObers…...

【前端 10】初探BOM
初探BOM:浏览器对象模型 在JavaScript的广阔世界中,BOM(Browser Object Model,浏览器对象模型)扮演着举足轻重的角色。它为我们提供了一套操作浏览器窗口及其组成部分的接口,让我们能够通过编写JavaScript…...
PostgreSQL入门与进阶学习,体系化的SQL知识,完成终极目标高可用与容灾,性能优化与架构设计,以及安全策略
专栏内容: postgresql使用入门基础手写数据库toadb并发编程 个人主页:我的主页 管理社区:开源数据库 座右铭:天行健,君子以自强不息;地势坤,君子以厚德载物. 文章目录 概述基础篇初级篇进阶篇…...

ODBC+FreeTDS从Linux访问Windows SqlServer数据库
提示 \color{red}{提示} 提示: 《Linux系统上编译安装FreeTDS库文件》中讲述了如何编译FreeTDS源码,并安装。 本文部分内容会在上述文章的基础上深入。 本文内容所使用的环境 Windows系统:Windows 10 企业版 64位操作系统;IP&a…...
Chainlit一个快速构建成式AI应用的Python框架,无缝集成与多平台部署
概述 Chainlit 是一个开源 Python 包,用于构建和部署生成式 AI 应用的开源框架。它提供了一种简单的方法来创建交互式的用户界面,这些界面可以与 LLM(大型语言模型)驱动的应用程序进行通信。Chainlit 旨在帮助开发者快速构建基于…...

leetcode日记(51)不同路径Ⅱ
和上一道题(无障碍物的最短路径)很像,但事实上比上一题多了优化方法 根据上一题改的代码如下,添加了对障碍物的判定,如果有障碍物则将数组值设为0。 class Solution { public:int uniquePathsWithObstacles(vector&l…...

图解分布式事务中的2PC与Seata方案
文章目录 文章导图什么是2PC解决传统2PC方案XA方案DTP模型举例:新用户注册送积分总结: Seata方案设计思想执行流程举例:新用户注册送积分 Seata实现2PC事务(AT模式)前提整体机制写隔离读隔离实际案例理解要点说明核心代…...
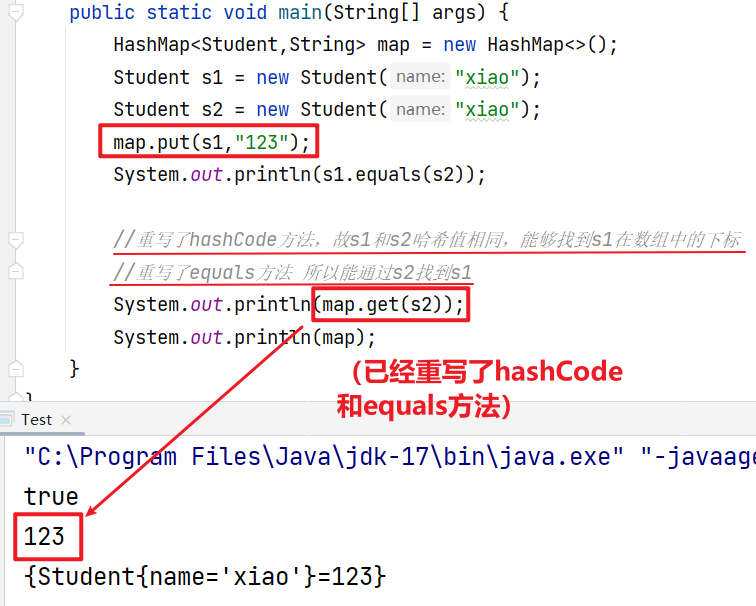
数据结构(Java):Map集合Set集合哈希表
目录 1、介绍 1.1 Map和Set 1.2 模型 2、Map集合 2.1 Map集合说明 2.2 Map.Entry<K,V> 2.3 Map常用方法 2.4 Map注意事项及实现类 3、Set集合 3.1 Set集合说明 3.2 Set常用方法 3.3 Set注意事项及其实现类 4、TreeMap&TreeSet 4.1 集合类TreeM…...

网络战时代的国家安全:策略、技术和国际合作
网络战时代的国家安全涉及到策略、技术和国际合作等多个方面。以下是对这些问题的简要概述: 网络战策略 网络战策略是指在现代战争中,通过网络技术进行的信息收集、处理、分析、调度和指挥等一系列行动,旨在同时影响和干扰对方的网络系统&am…...

【elasticsearch实现优先展示连词并按某个字段折叠显示最新一条】
elasticsearch实现优先展示连词并按某个字段折叠显示最新一条 前言match_phrase 顺序前缀 boost 权重collapse 折叠基本用法高级功能排序 前言 场景要求: 优先展示关键词连词的商品按照某个字段折叠相同字段,并按指定排序字段选择第一个 match_phras…...

Golang | Leetcode Golang题解之第284题窥视迭代器
题目: 题解: type PeekingIterator struct {iter *Iterator_hasNext bool_next int }func Constructor(iter *Iterator) *PeekingIterator {return &PeekingIterator{iter, iter.hasNext(), iter.next()} }func (it *PeekingIterator) hasNe…...

C语言中的结构体
文章目录 前言一、结构体是什么?二、结构体的定义三、结构体的初始化四、结构体的嵌套五、结构体数组 1结构体数组的定义:六、结构体指针 一、结构体是什么? 我们知道一群类型相同的数据组合到一起是数组,那一群不同类型的数据组…...
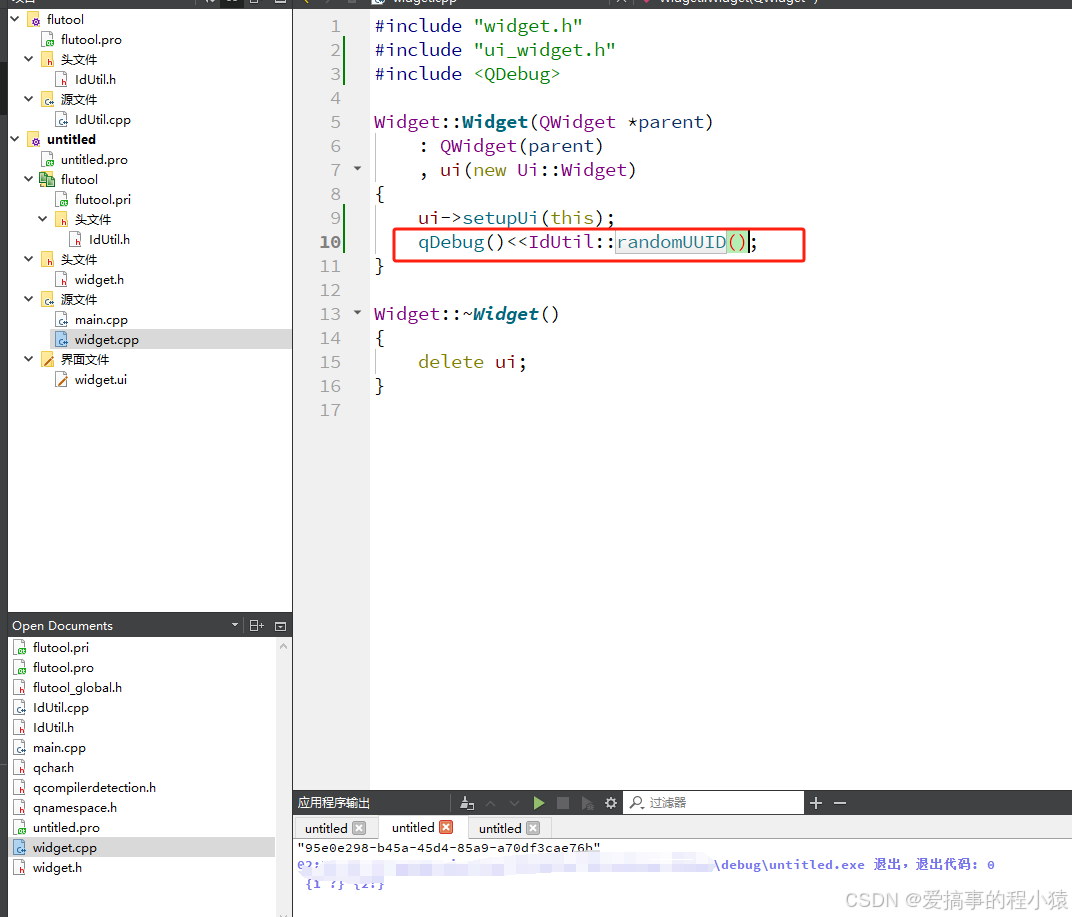
3.qml与c++模块化开发
目录 模块化开发封装c模块并使用封装qml模块并使用 模块化开发 什么是模块化开发呢? 举个例子: 我们有一台台式电脑,我们台式电脑有显卡,内存,磁盘,cpu,键盘,鼠标等 你可以将这些部…...
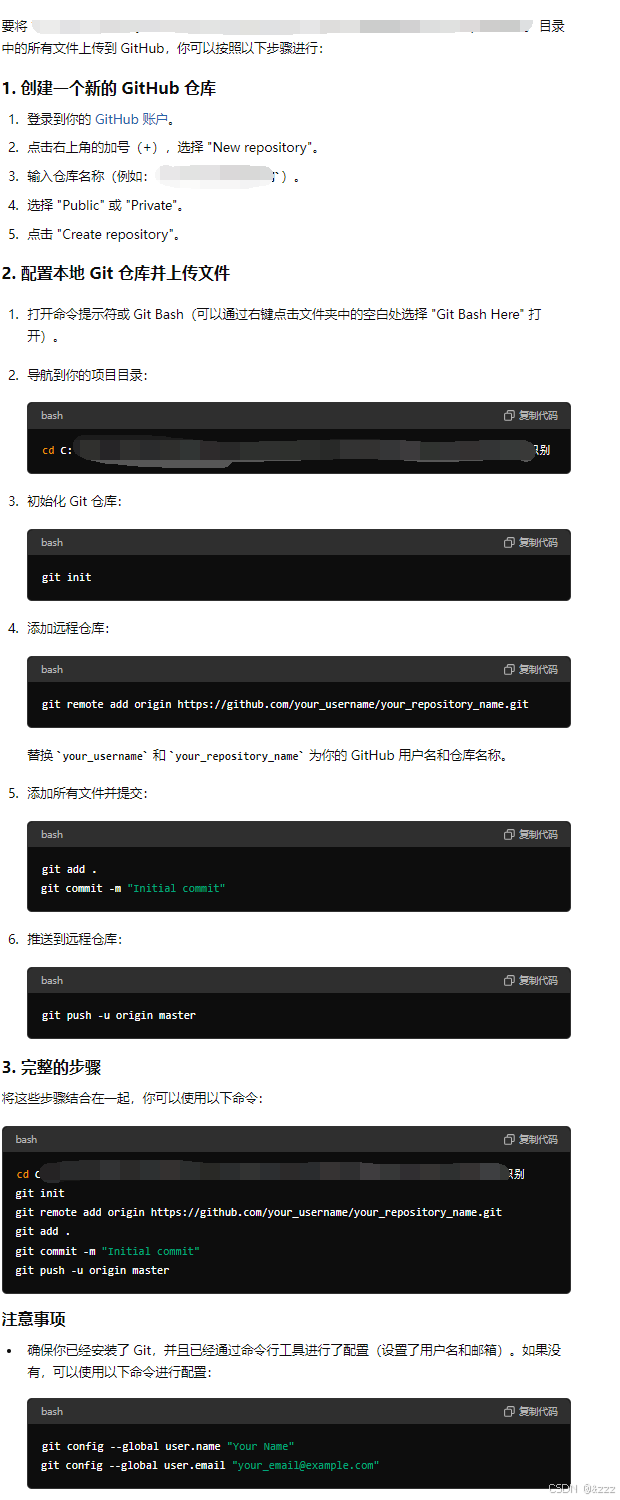
怎么使用github上传XXX内所有文件
要将 目录中的所有文件上传到 GitHub,你可以按照以下步骤进行: 创建一个新的 GitHub 仓库 登录到你的 GitHub 账户。 点击右上角的加号(),选择 “New repository”。 输入仓库名称(例如:202407…...
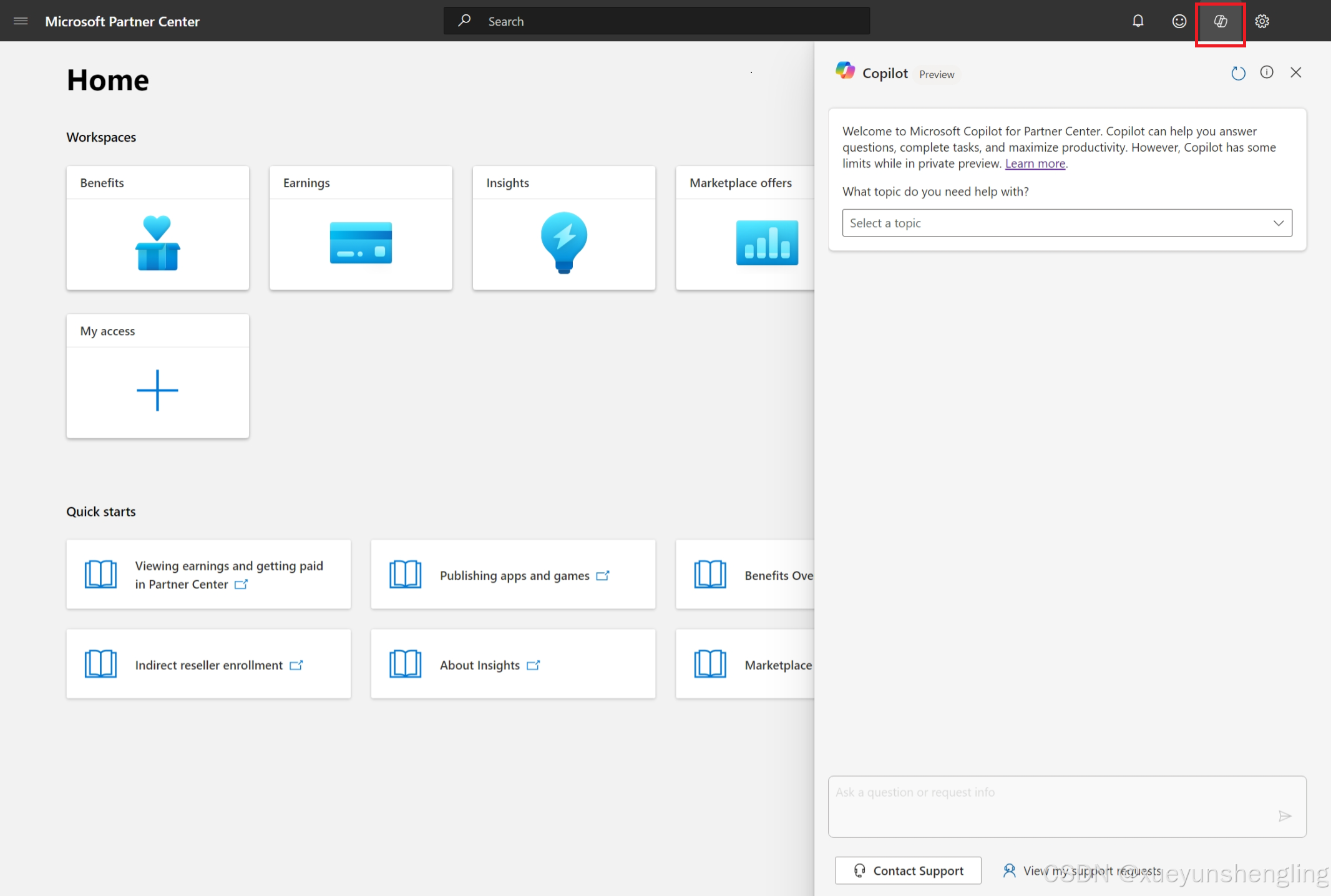
合作伙伴中心Partner Center中添加了Copilot预览版
目录 一、引言 二、Copilot 功能概述 2.1 Copilot 简介 2.2 Copilot 的核心功能 2.3 Copilot 的访问和使用 三、Copilot 的使用方法 3.1 Copilot 功能区域 3.2 Copilot 使用示例 3.2.1 编写有效提示 3.2.2 使用反馈循环 四、负责任的人工智能 4.1 Copilot 结果的可…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
