实分析与测度论问题的分类
实分析主要研究实数、实数序列、实数极限以及实值函数的分析,而度量空间则是一个具有距离函数的集合,其分类可以从多个角度进行。
实分析
实分析主要关注实数、实数序列、实数极限以及实值函数的分析。它涉及到多个重要的概念和理论,包括但不限于:
极限理论:包括数列的极限、函数的极限等。
数列极限:探讨数列的收敛性、极限的存在性及计算。
函数极限:研究函数在某点或无穷远处的极限行为,包括左右极限、无穷大或无穷小极限等。
连续性与可微性:研究函数的连续性、可微性等性质。讨论函数在某区间上的连续性,包括连续的定义、性质、间断点分类等。
积分理论:特别是勒贝格积分,它是对黎曼积分的推广,解决了黎曼积分无法处理的不连续函数等问题。
测度论:是研究度量空间上集合的“大小”或“长度”的数学分支,与积分理论紧密相关。
微分学
导数与微分:研究函数的导数定义、计算规则、几何意义及物理应用。
微分中值定理:如罗尔定理、拉格朗日中值定理等,探讨函数在区间上的变化性质。
泰勒公式与洛必达法则:用于函数近似计算及极限求解的重要工具。
积分学
黎曼积分与勒贝格积分:对比两种积分理论,探讨勒贝格积分对黎曼积分的推广及优势。
积分变换:如傅里叶变换、拉普拉斯变换等,在信号处理、图像处理等领域有广泛应用。
重积分与曲线、曲面积分:研究多元函数在不同区域上的积分计算及应用。
测度论
测度空间与可测集:定义测度空间,探讨可测集的性质及构造方法。
外测度与卡拉泰奥多里条件:研究外测度的性质及如何通过卡拉泰奥多里条件筛选可测集。
勒贝格积分理论:在测度论基础上建立的积分理论,适用于更广泛的函数类。
度量空间
度量空间是一个集合,其中的任意两个元素之间的距离是可定义的。度量空间是拓扑空间的一种,具有非常丰富的性质和应用。度量空间的分类可以从多个角度进行:
完备性:一个度量空间如果所有的柯西序列都收敛到空间中的点,则称该空间是完备的。例如,实数空间是完备的,而有理数空间不是。
有界性与完全有界性:有界度量空间指的是存在某个正数,使得空间中任意两点之间的距离都不超过这个数。完全有界空间则是指对于任意正数ε,都存在有限个半径为ε的开球,它们的并集覆盖整个空间。
紧致性:度量空间是紧致的,如果它的每一个序列都有一个收敛的子序列。紧致性在度量空间中是一个非常重要的性质,它与空间的连续性和完备性有紧密的联系。
可分性:如果一个度量空间包含一个可数稠密子集,则称该空间是可分的。可分性在研究度量空间的拓扑和几何性质时非常有用。
此外,度量空间还可以根据具体的度量函数进行分类,如欧几里得度量、曼哈顿度量、切比雪夫度量等。这些度量函数定义了空间中点与点之间的距离,从而决定了空间的几何和拓扑性质。
度量空间问题的分类
基本性质
距离函数与度量空间:定义度量空间中的距离函数,探讨其正定性、对称性和三角不等式性质。
开集、闭集与邻域:基于距离函数定义开集、闭集及点的邻域,研究它们的性质及相互关系。
拓扑性质
连通性:探讨度量空间中的连通区域及路径连通性。
紧致性:研究度量空间的紧致性条件、性质及在实数空间中的应用。
分离性质:如Hausdorff分离性质,探讨度量空间中集合的分离条件。
完备性
柯西序列与完备空间:定义柯西序列,探讨完备空间的性质及构造方法。
完备化:研究如何将非完备度量空间完备化,如实数集对有理数集的完备化。
特殊度量空间
欧几里得空间与希尔伯特空间:探讨这些特殊度量空间的性质、结构及在数学和物理中的应用。
函数空间:如Lp空间、连续函数空间等,研究这些函数空间的度量、收敛性及在泛函分析中的应用。
度量空间的分类与比较
等距同构与相似度量空间:探讨度量空间之间的等距同构关系及相似度量空间的性质。
嵌入与度量空间的复杂性:研究度量空间能否嵌入到更简单的空间中,以及度量空间的复杂性度量方法。
相关文章:

实分析与测度论问题的分类
实分析主要研究实数、实数序列、实数极限以及实值函数的分析,而度量空间则是一个具有距离函数的集合,其分类可以从多个角度进行。 实分析 实分析主要关注实数、实数序列、实数极限以及实值函数的分析。它涉及到多个重要的概念和理论,包括但…...
动态代理更改Java方法的返回参数(可用于优化feign调用后R对象的统一处理)
动态代理更改Java方法的返回参数(可用于优化feign调用后R对象的统一处理) 需求原始解决方案优化后方案1.首先创建AfterInterface.java2.创建InvocationHandler处理代理方法3. 调用 实际运行场景拓展 需求 某些场景,调用别人的方法࿰…...
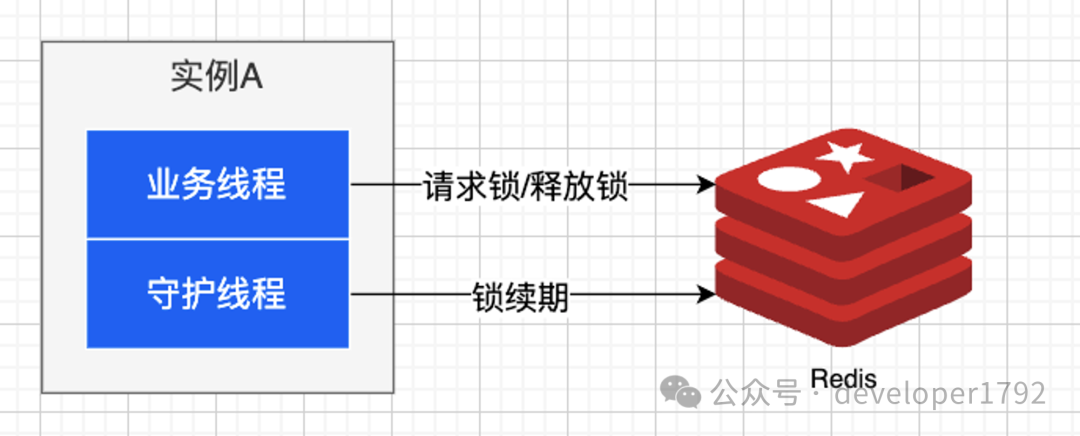
Redis缓存数据库进阶——Redis与分布式锁(6)
分布式锁简介 1. 什么是分布式锁 分布式锁是一种在分布式系统环境下,通过多个节点对共享资源进行访问控制的一种同步机制。它的主要目的是防止多个节点同时操作同一份数据,从而避免数据的不一致性。 线程锁: 也被称为互斥锁(Mu…...
)
网络芯片(又称为PHY网络芯片)
Realtek RTL8152B是一种常见的主板集成网络芯片(又称为PHY网络芯片)。PHY芯片是指将网络控制芯片的运算部分交由处理器或南桥芯片处理,以简化线路设计,从而降低成本。 https://www.realtek.com/Download/List?cate_id585 Realt…...
01 Go Web基础_20240728 课程笔记
概述 如果您没有Golang的基础,应该学习如下前置课程。 基础不好的同学每节课的代码最好配合视频进行阅读和学习,如果基础比较扎实,则阅读本教程巩固一下相关知识点即可,遇到不会的知识点再看视频。 视频课程 最近发现越来越多…...

嵌入式学习Day12---C语言提升
目录 一、指针数组 1.1.什么是指针数组 2.2. 格式 2.3.存储 2.4.与字符型二维数组相比 2.5.什么时候使用指针数组 2.6.练习 二、数组指针 2.1.什么是数组指针 2.2.格式 2.3.一维数组 2.3.特点 2.4.什么时候使用 三、指针和数组的关系 3.1.一维数组和指针 …...
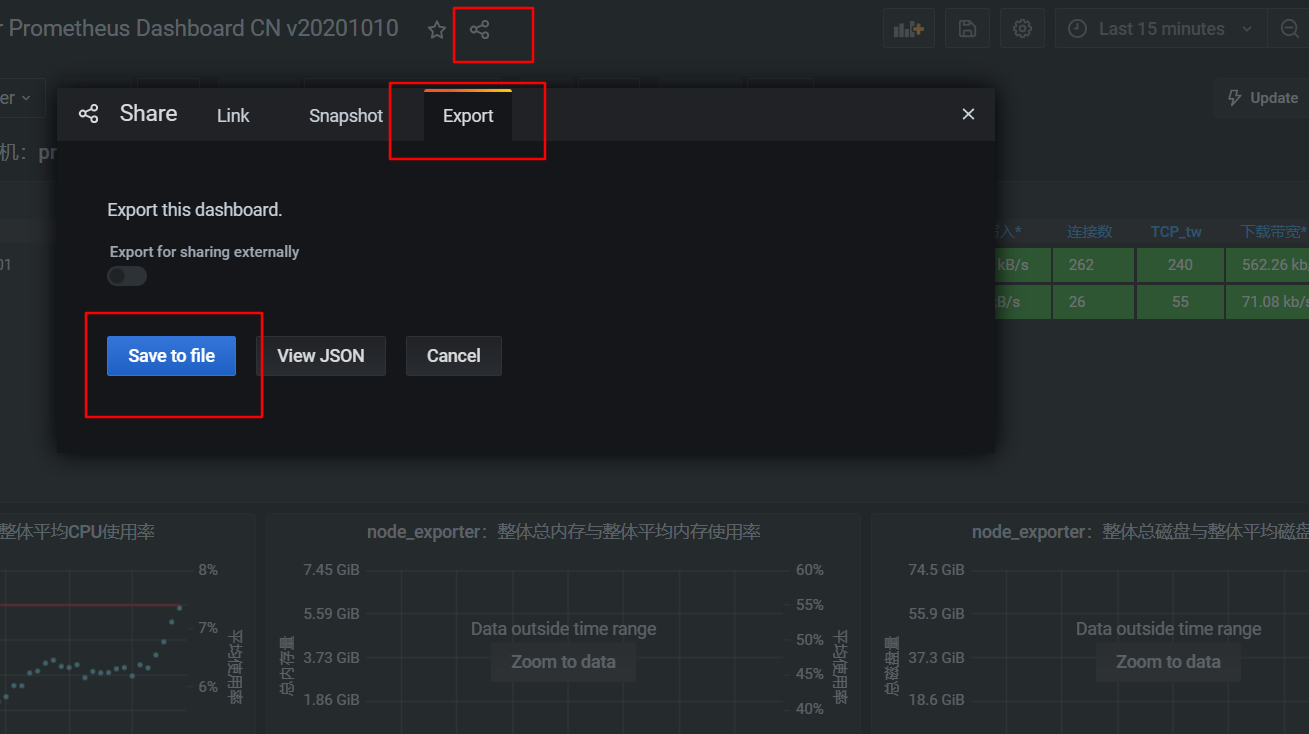
6.6 使用dashboard商城搜索导入模板
本节重点介绍 : 模板商城中搜索模板导入模板修改模板 大盘模板商城地址 免费的 地址 https://grafana.com/grafana/dashboards 搜索模板技巧 详情 导入dashboard 两种导入模式 url导入id导入json文件导入 导入 node_exporter模板 https://grafana.com/grafana/dashboa…...

一文讲透useMemo和useCallback
在React项目中是经常会使用到useMemo,useCallBack的,这是两个优化性能的方法,那么useMemo,useCallBack到底是什么呢?什么时候用呢? 下面将给打击分享相关知识,希望对大家有所帮助同时欢迎讨论指…...

【环境变量】安装了一个软件,如何配置环境变量?
配置环境变量为啥? 方便地在任何文件夹下调用某一指定目录下的文件。 配置步骤 以jdk17为例。 1.打开环境变量配置页面 2.新建一个变量,变量名为JAVA_HOME,内容为jdk的path路径 3.打开path变量,新建一个%JAVA_HOME%\bin&#x…...

重生之我当程序猿外包
第一章 个人介绍与收入历程 我出生于1999年,在大四下学期进入了一家互联网公司实习。当时的实习工资是3500元,公司还提供住宿。作为一名实习生,这个工资足够支付生活开销,每个月还能给父母转1000元,自己留2500元用来吃…...

我想给 git 分支换一个名字,应该怎么做?
Git中重命名分支的操作步骤如下: 确保你在要重命名的分支上。可以使用git branch或git status命令查看当前所在分支[1][2]. 使用以下命令重命名当前分支: git branch -m new-branch-name例如,将当前分支重命名为"feature-xyz": git branch -m feature-xyz-m参数是&q…...

echarts多stack的legend点选
echarts支持点击legend,实现显示和隐藏legend对应的数据,具体就是option里series里,name为legend值的数据。 如果配置了多个stack,那么可能你可能设置了多组legend,你点选的是多个legend组中的某组中的一个,那么如果不…...

搭建自己的金融数据源和量化分析平台(四):自动化更新上市公司所属一级、二级行业以及股票上市状态
前面做了更新沪深交易所的上市股票列表的读取和更新,但一旦股票退市则需要在数据库里将该股票状态更新为退市,同时附上退市日期,将股票名更改为XX退。 此外深交所下载的xls解析出来是没有上市公司所属的二级行业的,因此还需要建立…...

科创板重启IPO上会!募投审核新方向?思看科技等优化募投项目
撰稿 | 多客 来源 | 贝多财经 根据上交所项目审核动态最新公告,思看科技(杭州)股份有限公司(简称“思看科技”)将于8月2日上会,标志着时隔50天后科创板重新迎来首家上会企业,也标志着思看科技…...

深入解析损失函数:从基础概念到YOLOv8的应用
深入解析损失函数:从基础概念到YOLOv8的应用 在机器学习和深度学习中,损失函数是至关重要的组件,它们衡量模型的预测值与真实值之间的差距,从而指导模型的优化过程。本文将详细探讨损失函数的基本概念,及其在YOLOv8中…...

2.11.ResNet
ResNet 动机:我们总是想加更多层,但加更多层并不总是能改进精度 可以看出F1到F6模型越来越大,但F6距离最优解却总变远了,反而效果不好,通俗的来说就是学偏了,实际上我们希望是这样的: 更大…...

GitLab添加TortoiseGIT生成SSH Key
文章目录 前言一、PuTTYgen二、GitLab 前言 GitLab是一个用于托管代码仓库和项目管理的Web平台,公司搭建自己的gitlab来管理代码,我们在clone代码的时候可以选择http协议,也可以选择ssh协议来拉取代码。 SSH (Secure Shell)是一种通过网络进…...

20240729 大模型评测
参考: MMBench:基于ChatGPT的全方位多模能力评测体系_哔哩哔哩_bilibili https://en.wikipedia.org/wiki/Levenshtein_distance cider: https://zhuanlan.zhihu.com/p/698643372 GitHub - open-compass/opencompass: OpenCompass is an LLM evalua…...

基于微信小程序的校园警务系统/校园安全管理系统/校园出入管理系统
摘要 伴随着社会以及科学技术的发展,小程序已经渗透在人们的身边,小程序慢慢的变成了人们的生活必不可少的一部分,紧接着网络飞速的发展,小程序这一名词已不陌生,越来越多的学校机构等都会定制一款属于自己个性化的小程…...

达梦数据库归档介绍
一、什么是归档 数据库归档是一种数据管理策略,它涉及将旧的、不经常访问的数据移动到一个单独的存储设备,以便在需要时可以检索,同时保持数据库的性能和效率。 归档的主要目标是为了释放数据库中的空间,以便更有效地利用高性能…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
