KVM高级功能部署
一、概述
KVM(Kernel-based Virtual Machine)是一种基于内核的虚拟化技术,它依赖于CPU的虚拟化扩展(如Intel VT和AMD-V)来实现虚拟机的创建、管理和调度。KVM虚拟化技术因其高效、稳定的特点,在云计算和企业虚拟化环境中得到了广泛应用。本笔记将重点介绍KVM的高级功能部署,包括虚拟机迁移和KSM(Kernel SamePage Merging)内核同页合并。
二、KVM虚拟机迁移
1. 迁移的应用场景
KVM虚拟机迁移主要用于优化系统负载、重新规划虚拟机布局以及简化管理维护工作。具体应用场景包括:
- 宿主机负载高:当一台KVM宿主机的负载较高时,可将部分虚拟机迁移到负载较低的宿主机中,以保证服务质量。
- 资源节约:将多台负载较低的宿主机上的虚拟机集中迁移到一台宿主机上,以节约资源。
- 硬件升级:在升级宿主机硬件设备时,将虚拟机迁移到其他宿主机上,以实现业务不中断的硬件升级。
- 跨地域迁移:实现KVM虚拟机的远程迁移,支持跨地域的业务部署。
2. 迁移类型
KVM虚拟机迁移主要分为静态迁移和动态迁移两种:
- 静态迁移:需要关闭虚拟机,拷贝其磁盘文件和配置文件到目标宿主机,然后恢复启动。静态迁移期间,虚拟机服务会有一段时间不可用。
- 动态迁移:无需关闭虚拟机,即可在不同宿主机之间进行迁移。动态迁移可分为基于共享存储的动态迁移和基于数据块的动态迁移。
2.1 静态迁移步骤
- 准备虚拟机:在源宿主机上创建并配置好虚拟机。
- 提取磁盘和配置文件:关闭虚拟机,拷贝其磁盘文件和配置文件到目标宿主机。
- 配置和启动目标虚拟机:在目标宿主机上配置并启动虚拟机。
2.2 基于共享存储的动态迁移
- 配置NFS共享存储:在所有节点上安装NFS服务,并配置共享目录。
- 挂载NFS目录:在源宿主机和目标宿主机上挂载NFS目录。
- 创建虚拟机:在共享存储上创建虚拟机,并确保其配置文件和磁盘文件都存储在共享存储上。
- 执行迁移:使用KVM管理工具(如virsh)执行迁移操作。
2.3 基于数据块的动态迁移
基于数据块的动态迁移不需要共享存储,适用于本地存储的虚拟机。迁移过程中,KVM会处理数据的传输和同步,确保迁移过程中虚拟机服务不中断。
三、KSM内核同页合并
1. KSM简介
KSM(Kernel SamePage Merging)是一种内核功能,允许在两个或多个进程之间共享完全相同的内存页。KSM通过扫描正在运行的程序并比较它们的内存,将相同的内存页合并为一个单一的内存页,并标识为“写时复制(copy-on-write)”。当进程尝试修改这些内存页时,KSM会为其复制出一个新的内存页。
2. KSM的优势
- 节省内存:通过合并相同的内存页,KSM可以显著降低系统的内存使用量。
- 提高内存利用率:在KVM虚拟化环境中,多个虚拟机可能运行相同的操作系统或应用程序,使用KSM可以显著提高内存的利用率。
3. KSM的配置
- 安装和启动KSM:在KVM宿主机上安装并启动KSM服务。
- 配置KSM参数:根据实际需求配置KSM的参数,如合并内存的阈值、扫描间隔等。
- 监控和调整:监控KSM的性能和效果,并根据需要进行调整。
4. 注意事项
- CPU使用量:KSM会增加CPU的使用量,因为它需要扫描和比较内存页。因此,在配置KSM时需要考虑CPU的性能。
- 交换分区:为了防止内存过载,需要确保系统有足够的交换分区。
- 兼容性:KSM的效果与虚拟机操作系统及运行的应用程序有关,相同类型的操作系统和应用程序使用KSM的效果更佳。
相关文章:

KVM高级功能部署
一、概述 KVM(Kernel-based Virtual Machine)是一种基于内核的虚拟化技术,它依赖于CPU的虚拟化扩展(如Intel VT和AMD-V)来实现虚拟机的创建、管理和调度。KVM虚拟化技术因其高效、稳定的特点,在云计算和企…...
)
【C语言】柔性数组(打开前所未见的大门)
文章目录 前言柔性数组1.1 概念1.2 柔性数组的特点1.3 柔性数组的使用1.4 柔性数组的优势 总结 前言 说到柔性数组,相信有很多学过C语言的读者都不知道这是个什么东西。不过没有关系,相信本章能够带你从到认识到掌握柔性数组,做一个充满知识…...

设计模式17-适配模式
设计模式17-适配模式 动机定义与结构C代码推导总结应用具体应用示例 动机 在软件系统中由于应用环境的变化常常需要将一些现存的对象。放到新的环境中去应用。但是新环境要求的接口是这些现存对象所不满足的。那么这种情况下如何应对这种迁移的变化?如何既能利用现…...

react ant Input defaultValue={value}设置了value值以后,但是defalult没有赋值上,输入框也没有显示
在 React 中,defaultValue 是一个非受控属性,而 value 是一个受控属性。这两个属性都可以用于设置 Input 组件的值,但是它们的工作方式有所不同。 value:这是一个受控属性,意味着输入框的值由 React 状态控制。每当状态…...

大模型开发如何把一段文字变成一组token?
在大模型开发中,将一段文字变成一组token通常称为"tokenization"(分词)。这是自然语言处理中的一个关键步骤,主要是将连续的文本划分成离散的单元(token),这些单元可以是单词、子词或…...

【MSYS】Windows Terminal 集成
Windows Terminal 集成 MSYS2安装在默认位置C:\msys64打开Windows Terminal打开JSON配置文件文件。 添加如下配置: "profiles": {"defaults": {},"list": [{"guid": "{71160544-14d8-4194-af25-d05feeac7233}"…...

Python酷库之旅-第三方库Pandas(056)
目录 一、用法精讲 211、pandas.Series.truncate方法 211-1、语法 211-2、参数 211-3、功能 211-4、返回值 211-5、说明 211-6、用法 211-6-1、数据准备 211-6-2、代码示例 211-6-3、结果输出 212、pandas.Series.where方法 212-1、语法 212-2、参数 212-3、功能…...

ZBrush入门使用介绍——4、笔刷选项说明
大家好,我是阿赵。 这次来看看ZBrush的笔刷的选项用法。 一、选择笔刷 点击笔刷,可以打开笔刷选择面板。 在最上面的Quick Pick,有最近使用过的笔刷,可以快速的选择。下面有很多可以选择的笔刷。但由于笔刷太多,…...

Java每日一练,技术成长不间断
目录 题目1.下列关于继承的哪项叙述是正确的?2.Java的跨平台特性是指它的源代码可以在多个平台运行。()3.以下 _____ 不是 Object 类的方法4.以下代码:5.下面哪个流类不属于面向字符的流()总结 题目 选自牛…...

传知代码-上下位关系自动检测方法(论文复现)
代码以及视频讲解 本文所涉及所有资源均在传知代码平台可获取 概述 本文复现论文 Hearst patterns revisited: Automatic hypernym detection from large text corpora[1] 提出的文本中上位词检测方法。 在自然语言处理中,上下位关系(Is-a Relations…...
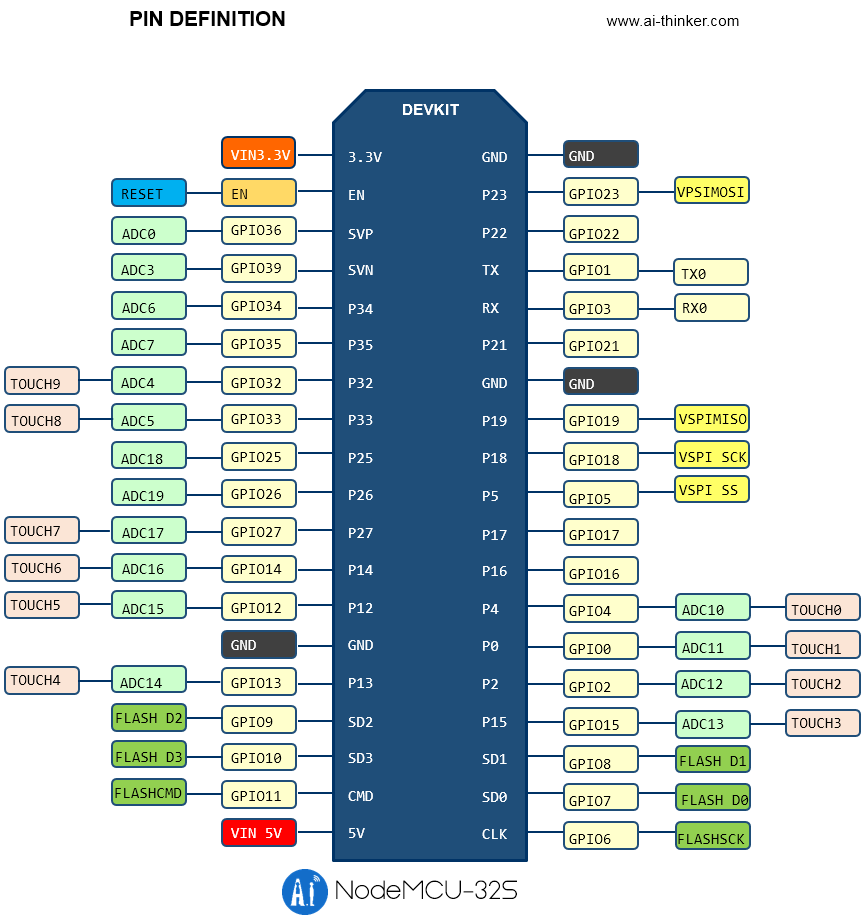
从零开始的MicroPython(二) GPIO及代码应用
上一篇:http://t.csdnimg.cn/mg2Qt 文章目录 ESP32(NodeMCU-32S)简介引脚注意事项 类与对象的概念MicroPython的GPIO使用文档解释machine.PinPin.irq 点灯 ESP32(NodeMCU-32S) 简介 NodeMCU-32S 是安信可基于 ESP32-32S 模组所设计的核心开发板。该开发板延续了 N…...

嵌入式day15
数组指针 能够指向整个数组 一维数组: &a,考察a的数据类型 int(*p)[10]:表示一个指向长度为10的一维整型数组的指针 二维数组: 指向函数的指针 函数的函数名,即为函数的入口地址&#x…...

【电池管理系统(BMS)-01】 | 电池管理系统简介,动力电池和储能电池区别
🎩 欢迎来到技术探索的奇幻世界👨💻 📜 个人主页:一伦明悦-CSDN博客 ✍🏻 作者简介: C软件开发、Python机器学习爱好者 🗣️ 互动与支持:💬评论 &…...

C++ STL partial_sum 用法
一:功能 计算部分和,即遍历序列中每个元素,计算前 i 个元素的累加和,并将结果存在 i 的位置上。 二:用法 #include <iostream> #include <vector> #include <numeric>int main() {std::vector<…...

诚宜开张圣听不应妄自菲薄
拾人牙慧孜孜不倦 青山依旧在几度夕阳红朝闻道夕死可矣 青山依旧在几度夕阳红 安能以血补天我计不成乃天命也臣本布衣躬耕南阳大丈夫宁死不辱尔要试我宝剑是否锋利吗又待怎样休教天下人负我竖子不足与谋皇天不佑天下英雄唯使君与操尔青光殷殷其灿如炎备不量力欲申大义于天下我…...

Vue3 加载条(LoadingBar)
效果如下图:在线预览 APIs LoadingBar 参数说明类型默认值必传containerClass加载条容器的类名stringundefinedfalsecontainerStyle加载条容器的样式CSSProperties{}falseloadingBarSize加载条大小,单位 pxnumber2falsecolorLoading加载中颜色string‘…...

《CSS创意项目实战指南》:点亮网页,从实战中掌握CSS的无限创意
CSS创意项目实战指南 在数字时代,网页不仅是信息的载体,更是艺术与技术的融合体。通过CSS,你可以将平凡的网页转变为引人入胜的视觉盛宴,让用户体验跃升至全新高度。《CSS创意项目实战指南》正是这样一本引领你探索CSS无限可能的…...

[FBCTF2019]RCEService (PCRE回溯绕过和%a0换行绕过)
json格式输入ls出现index.php 这道题原本是给了源码的,BUUCTF没给 源码: <?phpputenv(PATH/home/rceservice/jail);if (isset($_REQUEST[cmd])) {$json $_REQUEST[cmd];if (!is_string($json)) {echo Hacking attempt detected<br/><br/…...

vue3后台管理系统 vue3+vite+pinia+element-plus+axios上
前言 项目安装与启动 使用vite作为项目脚手架 # pnpm pnpm create vite my-vue-app --template vue安装相应依赖 # sass pnpm i sass # vue-router pnpm i vue-router # element-plus pnpm i element-plus # element-plus/icon pnpm i element-plus/icons-vue安装element-…...

Mysql的事务隔离级别实现原理
一、事务隔离级别 mysql支持四种事务隔离级别: 读未提交:一个事务可以读取到另一个事务还未提交的数据;读已提交:一个事务可以读取到另一个事务已经提交的数据;可重复读:同一个事务中,无论读取…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
