数据结构之探索“堆”的奥秘
找往期文章包括但不限于本期文章中不懂的知识点:
个人主页:我要学编程(ಥ_ಥ)-CSDN博客
所属专栏:数据结构(Java版)
目录
堆的概念
堆的创建
时间复杂度分析:
堆的插入与删除
优先级队列
PriorityQueue的特性
PriorityQueue源码分析
PriorityQueue常用接口介绍
构造方法:
堆的应用
堆的概念
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储(从上到下、从左到右)在 一个一维数组 中,并满足:Ki <= K(2i+1) 且 Ki<=K(2i+2) (Ki >= K(2i+1) 且 Ki >= K(2i+2) ) i = 0,1,2…,则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
注意:Ki <= K(2i+1) 且 Ki<=K(2i+2) 这个公式就是说明根结点的值小于等于左右孩子节点的值,即小根堆或者最小堆。与其相反就是根结点的值大于等于左右孩子节点,即大根堆或者最大堆。
堆的性质:
1、堆中某个节点的值总是不大于或不小于其父节点的值;
例如:小根堆就是根结点的值小于等于孩子节点的值,也就是说孩子节点的值大于等于根结点的值,也就对应了孩子节点不小于其父节点;反之,就是大根堆的性质了。
2、堆总是一棵完全二叉树。
因为堆是把数据按照完全二叉树的方式存储在一个一维数组中的。
3、堆的根结点总是这个一维数组中的最值,要么是最大值,要么是最小值。
如果是大根堆,按照 性质1 的推论就是:根结点的值大于等于孩子节点的值。这样一直递归下去,根结点肯定就是最大的。最坏情况就是所有结点的值全部相等。
4、堆的存储结构是一个一维数组,但是其逻辑结构是一个完全二叉树。
为什么不能是一个普通的二叉树呢?因为普通的二叉树会有空节点(空树),这样在数组中就会null元素的存在,导致了空间利用率比较低。
堆的创建
现有一组数据 {0,1,2,3,4,5,6,7,8,9} 我们要把这组数据组织成大根堆。
public class Heap {int[] elem;int usedSize;public Heap(int k) {elem = new int[k];}public Heap() {elem = new int[10];}// 给堆初始化数据public void initHeap(int[] array) {for (int i = 0; i < array.length; i++) {elem[i] = array[i];usedSize++;}}
}思路:大根堆的特点是根结点的值大于左右孩子节点的值。这里采用的是一种向下调整的方法。
即从最后一棵树的根结点位置开始进行调整大根堆,一直调整到整棵树的根结点满足大根堆。

// 创建大根堆
public void createHeap() {// 从最后一棵子树的根结点位置开始for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {// 向下调整的方法:从要调整的位置开始,到整棵树结束siftDown(parent, usedSize);}
}private void siftDown(int parent, int usedSize) {int child = parent * 2 + 1;// 只有当孩子节点在有效数据之内时,才能调整while (child < usedSize) {// 先找到左右孩子节点的最大值if (child+1 < usedSize && elem[child] < elem[child+1]) { // 得确保右孩子存在child++;}// 比较孩子节点的最大值和根结点的值if (elem[parent] < elem[child]) {// 交换swap(elem, parent, child);// 交换完成只是本级满足了大根堆的条件,但是交换下去的值不一定满足当级的大根堆条件parent = child;child = parent * 2 + 1;} else {// 满足大根堆就不需要继续调整了break;}}
}private void swap(int[] elem, int i, int j) {int tmp = elem[i];elem[i] = elem[j];elem[j] = tmp;
}这里可能有几个小伙伴们疑惑的地方:
1、为什么交换完成之后还要再进行向下调整判断是否需要交换?

总而言之就是一句话:参与调整的,就得再次进行判断是否符合大根堆。
2、为什么本级满足大根堆的情况后,就不需要继续往下判断是否调整?
因为我们是从下面开始调整的,如果本级满足了大根堆,那么下面的就一定也满足大根堆。因此就无需继续判断了。
时间复杂度分析:

将上面的所有结果相加,就是最终的时间复杂度。

因此向下调整建堆的时间复杂度是:O(N)。
堆的插入与删除
堆的插入:
思路:因为堆在存储上是一个数组,那么我们肯定是按照插入数组元素的方法来进行插入,即尾插。尾插完之后,还得进行判断这个新的堆是否是大根堆。因为这个的判断方式是从插入的节点开始往上判断,因此这个判断是向上调整。
public void offer(int val) {// 插入的元素放到最后,然后其所在的树进行向上调整// 判满,扩容if (isFull()) {elem = Arrays.copyOf(elem, elem.length*2);}elem[usedSize++] = val;siftUp(usedSize-1, 0);}private boolean isFull() {return usedSize == elem.length;}private void siftUp(int child, int end) {// 因为原来是满足大根堆的,因此我们只需要判断这个新插入的元素是否也满足int parent = (child-1) / 2;while (parent >= end) {if (elem[child] > elem[parent]) {// 交换swap(elem, child, parent);child = parent;parent = (child-1) / 2;} else {// 因为原来是满足大根堆的,如果这个也满足,那么就全部满足了break;}}}有了插入方法,我们也就可以通过插入来创建堆了。
注意:我们手动创建堆的方法是采用向下调整,而插入元素采用的是向上调整。因此,两者创建出来的堆结果会不一样,但都是大根堆。
向上调整建堆的时间复杂度分析:
与向下调整相比,向上调整还要把最后一层的节点全部调整,因此,向上调整的时间复杂度肯定是大于向下调整的。

向上调整建堆的时间复杂度O(N+logN) 。
堆的删除:
思路:堆的删除,我们采取的方式也和数组类似,是把堆顶元素与最后一个元素交换,再进行向下调整。
public int poll() {// 判空,抛异常if (isEmpty()) {throw new HeapIsEmptyException("堆为空异常");}int val = elem[0];swap(elem, 0, usedSize-1);siftDown(0, usedSize-1);usedSize--;return val;}private boolean isEmpty() {return usedSize == 0;}堆的删除的时间复杂度:O(logN)。
交换完,向下调整就只调整树的高度,也就是logN。
堆的插入的时间复杂度:O(logN)。
插在最后,然后进行向上调整,也是调整树的高度。
获取堆顶元素:
public int peek() {if (isEmpty()) {throw new HeapIsEmptyException("堆为空异常");}return elem[0];}看到这里,我们就应该可以猜出堆和队列是有关系的,否则,不会把队列的方法名给堆。堆这种数据结构可以实现优先级队列。
优先级队列
通过堆的性质3,我们就可以推出一个结论:如果我们每次从堆中删除数据一定删除的是优先级最高的。如果是小根堆,那么就是删除最小值,如果是大根堆,那么删除的就是最大值。即优先级最高的先被删除。这就对应了队列中的一个特殊队列:优先级队列。实际上JavaAPI中优先级队列底层就是通过堆来实现的。
PriorityQueue的特性
1、使用时必须导入PriorityQueue所在的包,即:
import java.util.PriorityQueue;2、PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出 ClassCastException异常。
因为堆中的元素是需要可以比较大小。否则,无法判别优先级。
3、不能插入null对象,否则会抛出NullPointerException。
因为我们去比较的时候,是通过对象调用专属的比较方法,如果对象为null,就会发生空指针异常。
4、PriorityQueue默认情况下是小堆---即每次获取到的元素都是最小的元素。
5、其内部可以自动扩容,无需我们主动实现。
PriorityQueue源码分析


PriorityQueue常用接口介绍
构造方法:
| 构造器 | 功能介绍 |
| PriorityQueue() | 创建一个空的优先级队列,默认容量是11 |
| PriorityQueue(int initialCapacity) | 创建一个初始容量为initialCapacity的优先级队列,注意: initialCapacity不能小于1,否则会抛IllegalArgumentException异常 |
| PriorityQueue(Collection c) | 用一个集合来创建优先级队列 |
使用:
public class Test {public static void main(String[] args) {// 创建一个优先级队列,默认容量11PriorityQueue<Integer> priorityQueue1 = new PriorityQueue<>();// 创建一个优先级队列,容量是20PriorityQueue<Integer> priorityQueue2 = new PriorityQueue<>(20);List<Integer> list = new ArrayList<>();list.add(1);list.add(2);list.add(3);list.add(4);list.add(5);// 创建一个优先级队列(容量根据list的大小来分配)PriorityQueue<Integer> priorityQueue3 = new PriorityQueue<>(list);// 长度System.out.println(priorityQueue3.size());// 小根堆System.out.println(priorityQueue3.poll());}
}这里的“容量根据list的大小来分配”的意思是:本来的默认容量是11,如果list的长度大于11,那么就会按照2倍或者1.5倍去扩容。
插入/删除/获取优先级最高的元素
| 函数名 | 功能介绍 |
| boolean offer(E e) | 插入元素e,插入成功返回true,如果e对象为空,抛出NullPointerException异常,时间复杂度O(log2 N),注意:空间不够时候会进行扩容 |
| E peek() | 获取优先级最高的元素,如果优先级队列为空,返回null |
| E poll () | 移除优先级最高的元素并返回,如果优先级队列为空,返回null |
| int size() | 获取有效元素的个数 |
| void clear() | 清空 |
| boolean isEmpty() | 检测优先级队列是否为空,空返回true |
堆的应用
1、PriorityQueue的实现。
2、堆排序。
不同的顺序,建立不同的堆,但是一定是后面的元素先有序,再是前面的元素有序。
因此我们就可以知道:如果是从小到大排序,那么就要建大根堆;反之,则是建小根堆。
因为 如果是从小到大排序,且后面的元素先有序,那么后面的元素只能是最大的,因此建立大根堆的话,堆顶元素一定是最大的。这时,我们只需把堆顶元素和最后一个元素进行交换,然后再进行向下调整,直至调整到整棵树的根节点。
代码实现:
public void heapSort() {int j = 0;for (int i = usedSize-1; i > 0; i--) {swap(elem,i,j);siftDown(0, i);}}3、Top-k问题
TOP-K问题:即求数据集合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大,且K都比较小。
例如:全球前500强的企业。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
如果是要找前K个最小的元素,将前K个元素建成大根堆,然后再去遍历后N-K个元素,遇到小于堆顶元素的就交换,遍历完成后剩下的堆中元素就是前K个最小的。
练习:面试题 17.14.最小K的个数
题目:
设计一个算法,找出数组中最小的k个数。以任意顺序返回这k个数均可。
示例:
输入: arr = [1,3,5,7,2,4,6,8], k = 4 输出: [1,2,3,4]提示:
0 <= len(arr) <= 1000000 <= k <= min(100000, len(arr))
思路一:直接排序,然后遍历前K个即可。
public int[] smallestK(int[] arr, int k) {// 调用JavaAPI提供的方法才行,自己实现的方法会超出时间限制Arrays.sort(arr); // 默认是从小到大排序int[] ret = new int[k];for (int i = 0; i < k; i++) {ret[i] = arr[i];}return ret;}
思路二:将N个元素建成小根堆,然后每次取堆顶元素,取K次即可。
public int[] smallestK(int[] arr, int k) {PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();for (int i = 0; i < arr.length; i++) {priorityQueue.offer(arr[i]);}// 上面是建成的小根堆int[] ret = new int[k];for (int i = 0; i < k; i++) {ret[i] = priorityQueue.poll();}return ret;}思路三:取前K个元素建成大根堆,然后再遍历剩下的元素,如果小于堆顶元素,则交换。
class Solution {public int[] smallestK(int[] arr, int k) {int[] ret = new int[k];if (k == 0 || arr == null) {return ret;}PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(k, new Incompare());for (int i = 0; i < k; i++) {priorityQueue.offer(arr[i]);}for (int i = k; i < arr.length; i++) {if (priorityQueue.peek() > arr[i]) {priorityQueue.poll();priorityQueue.offer(arr[i]);}}for (int i = 0; i < k; i++) {ret[i] = priorityQueue.poll();}return ret;}
}// 创建新的比较器
class Incompare implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o2.compareTo(o1);}
}
好啦!本期 数据结构之探索“堆”的奥秘 的学习之旅就到此结束啦!我们下一期再一起学习吧!
相关文章:

数据结构之探索“堆”的奥秘
找往期文章包括但不限于本期文章中不懂的知识点: 个人主页:我要学编程(ಥ_ಥ)-CSDN博客 所属专栏:数据结构(Java版) 目录 堆的概念 堆的创建 时间复杂度分析: 堆的插入与删除 优先级队列 PriorityQ…...

光影漫游者:高科技球形场馆开启沉浸式体验新时代—轻空间
轻空间(江苏)膜科技有限公司的自主品牌“QSPACE轻空间”推出的“光影漫游者”,是一款突破传统的创新球形场馆。这款产品自问世以来,以其独特的设计和卓越的功能迅速成为各类活动和展览的焦点。光影漫游者不仅以其时尚的外观吸引了…...

面试题007:static修饰符可以修饰什么,static的重要规则
在Java类中,可用static修饰属性、方法、代码块、内部类 。static关键字修饰的成员被称为静态成员。 被修饰后的成员具备以下特点: 随着类的加载而加载 优先于对象存在 修饰的成员,被所有对象所共享 访问权限允许时,可不创建对…...
EasyTwin的动画系统已经到了next level?快来一探究竟!
在实际的数字孪生项目场景建设中,水利项目中的洪水推演、工业领域的工程施工模拟、车间产线运转、机械装置和零件配置展示等项目场景,都对动画效果有很强的使用需求,这是对渲染软件和设计师能力的极大考验🆘。 别担心!…...

当业务开展遇到阻力,如何开展?
1:先够通问题,看能否通过及时的沟通解决掉问题阻力(相信你已经做过了无功而返) 2:全面思考这个问题,这个事情对方做了对他有什么好处?对大家的公共目标有什么好处?尝试说服 3&#x…...

萨科微半导体整流桥
金航标kinghelm萨科微总经理宋仕强介绍说,萨科微半导体的整流桥热销型号及其主要参数?萨科微的整流桥热销型号有 DB207S,其主要参数有:反向工作电压(VRRM)为 1000V、直流输出电流(Io)为 2.0A、…...

STM32的GPIO输入输出方式设置示例
1、GPIO口做基本的输入/输出口使用时,输入有上拉输入、下拉输入、浮空输入(既无上拉电阻也无下拉电阻)3种输入方式;输出有开漏输出、推挽输出2种输出方式。 2、示例 (1)示例1:GPIO做输出的设置…...

SQL插入、更新和删除数据
SQL插入、更新和删除数据 一、直接向表插入数据 1.1、插入完整的行 这里所说的完整行指的是包含表内所有字段的数据行;假设表中有n个字段,则插入完整行的语法: INSERT INTO 表名或视图名 VALUES(字段1的值,字段2的值,字段3的值,...,字段n的…...

如何将幻灯片中的图片背景设置为透明
在制作幻灯片时,我们经常需要插入图片来丰富内容,提升视觉效果。但有时,图片的背景可能会干扰幻灯片的整体设计,这时将图片背景设置为透明就显得尤为重要。本文将详细介绍如何在常用的幻灯片制作软件中实现这一效果,帮…...

【雅思考试】-- Day2 - 单词
雅思单词 WordPOSDefinitionWordPOSDefinition1reliabilityn.可靠性16facilitatev.促进;助长2goaln.目标17expectationn.期待;期望;预期3strengthn.力量;力气;实力18reinforcen.加强;加固;强化4…...

.\venv\Scripts\activate : 无法加载文件 E:\,因为在此系统上禁止运行脚本。
问题描述: 问题原因: Windows PowerShell 的执行策略用于控制脚本的运行权限和安全性。 以下是几种常见的执行策略及其特点: AllSigned:只允许运行经过数字签名的脚本。这意味着无论是本地创建的还是从网络获取的脚本࿰…...

C++之explicit
在 C 中,explicit 是一个关键字,用于修饰单参数的构造函数,防止它们被用于隐式类型转换。理解 explicit 关键字涉及以下几个方面: 1. 隐式类型转换 在 C 中,单参数的构造函数可以被用于执行隐式类型转换,…...
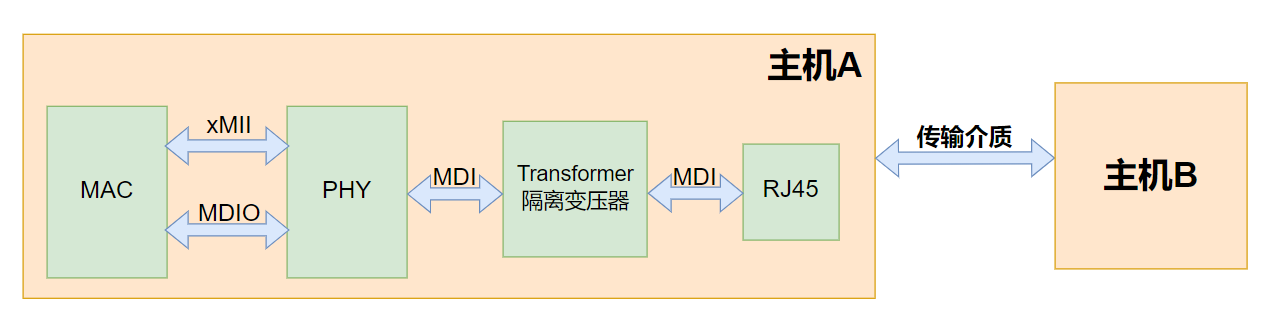
基于FPGA的以太网设计(4)----详解PHY的使用(以YT8531为例)
目录 1、前言 2、如何了解PHY芯片? 2.1、总览 2.2、管脚 2.3、编码 2.4、自协商 2.5、环回模式 2.6、睡眠模式 2.7、复位 2.8、PHY地址 3、PHY芯片的寄存器配置 3.1、Basic Control Register (0x00) 3.2、Basic StatusRegister (0x01) 3.3、PHY Specific Status…...
机器学习之心一区级 | Matlab实现SMA-Transformer-LSTM多变量回归预测(黏菌算法优化)
机器学习之心一区级 | Matlab实现SMA-Transformer-LSTM多变量回归预测(黏菌算法优化) 目录 机器学习之心一区级 | Matlab实现SMA-Transformer-LSTM多变量回归预测(黏菌算法优化)效果一览基本介绍程序设计参考资料 效果一览 基本介…...

idea导入项目根目录缺失解决方法
点击File→Project Structure 在弹出的界面选择Modules→→import Module,然后选择你导入文件点击OK, 选择导入类型next→勾选Search for projects recursively(递归寻找项目)→next→Finish最后选择根目录点击OK即可。...

VMware虚拟机下ubuntu配置
VMware虚拟机下ubuntu配置 1 Ubuntu换源2 安装VMware Tools2.1 一般安装2.2 代码安装 3 安装中文输入法参考 VMware虚拟机安装及虚拟机下安装ubuntu可参见另一博客-VMware虚拟机安装及虚拟机下安装ubuntu 1 Ubuntu换源 Ubuntu换源的主要用途是通过更换软件源来提高软件下载速…...

回调函数复习
#include <iostream>// 定义一个回调函数类型 typedef void (*CallbackFunction)(int);// 函数接受一个回调函数作为参数 void performOperation(int value, CallbackFunction callback) {// 执行某些操作std::cout << "Performing operation with value: &qu…...

开源AI智能名片O2O商城微信小程序在顾客价值链优化中的应用与探索
摘要:随着信息技术的飞速发展,顾客的消费行为模式正经历着前所未有的变革。在这一背景下,开源AI智能名片O2O商城微信小程序作为一种创新的营销与服务平台,正逐步成为企业连接顾客、优化顾客价值链的重要工具。本文旨在探讨开源AI智…...

idea-springboot后端所有@注释含义汇总-持续更新!
(1)启动类 ①SpringBootApplication 出现这个代表这个就是整个程序的入口,是运行的开始位置 ②ComponentScan("com.example.dao.impl") 启动时自动扫描制定beans包 (2)mapper层(Dao层…...

七:C语言-数组
七:C语言-数组 数组是一组相同类型元素的集合数组中存放的是1个或者多个数据,但是数组元素个数不能为0数组中存放的多个数据,类型是相同的数组分为一维数组和多维数组,多维数组一般比较多见的是二维数组存放在数组中的值被称为数…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
